Does this sound familiar: "I started to do web development after taking courses"?Perhaps you want to improve your knowledge of the basics of computer science in terms of data structures and algorithms. Today we’ll talk about some of the most common data structures using the JS example.1. Stack (calls) (Stack)
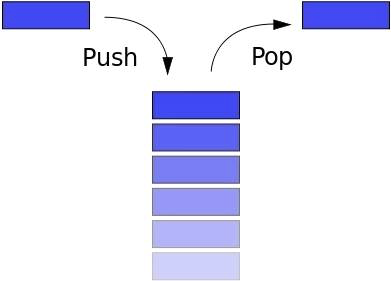The stack follows the LIFO principle (Last In First Out - Last In, First Out). If you stacked the books on top of each other and wanted to take the lowest book, then first take the top one, then the next one, etc. The "Back" button in the browser allows you to go (return) to the previous page.The stack has the following methods:- push: add new item
- pop: remove top element, return it
- peek: return top element
- length: return the number of elements on the stack
An array in JS has stack attributes, but we will build it from scratch using function Stack ():function Stack() {
this.count = 0
this.storage = {}
this.push = function(value) {
this.storage[this.count] = value
this.count++
}
this.pop = function() {
if (this.count === 0) return undefined
this.count--
let result = this.storage[this.count]
delete this.storage[this.count]
return result
}
this.peek = function() {
return this.storage[this.count - 1]
}
this.size = function() {
return this.count
}
}
2. Queue (Queue)
A queue resembles a stack. The difference is that the queue follows the FIFO principle (First In First Out - first in, first out). When you stand in line, the first in it will always be the first.The queue has the following methods:- enqueue: enter the queue, add an item to the end
- dequeue: leave the queue, delete the first element and return it
- front: get the first element
- isEmpty: check if the queue is empty
- size: get the number of items in the queue
An array in JS has some queue attributes, so we can use it for demonstration:function Queue() {
let collection = []
this.print = function() {
console.log(collection)
}
this.enqueue = function(element) {
collection.push(element)
}
this.dequeue = function() {
return collection.shift()
}
this.front = function() {
return collection[0]
}
this.isEmpty = function() {
return collection.length === 0
}
this.size = function() {
return collection.length
}
}
The order of priority (priority)
The queue has an advanced version. Assign each item a priority and the items will be sorted accordingly:function PriorityQueue() {
...
this.enqueue = function(element) {
if (this.isEmpty()) {
collection.push(element)
} else {
let added = false
for (let i = 0; i < collection.length; i++) {
if (element[1] < collection[i][1]) {
collection.splice(i, 0, element)
added = true
break;
}
}
if (!added) {
collection.push(element)
}
}
}
}
Testing:let pQ = new PriorityQueue()
pQ.enqueue([gannicus, 3])
pQ.enqueue([spartacus, 1])
pQ.enqueue([crixus, 2])
pQ.enqueue([oenomaus, 4])
pQ.print()
Result:[
[spartacus, 1],
[crixus, 2],
[gannicus, 3],
[oenomaus, 4]
]
3. A linked list (linked list of nodes and links or pointers) (Linked List)
Literally, a linked list is a chained data structure, where each node consists of two parts: node data and a pointer to the next node. The linked list and conditional array are linear data structures with serialized storage. The differences are as follows:A singly linked list has the following methods:- size: return the number of nodes
- head: return the first element (head - head)
- add: add an element to the end (tail - tail)
- remove: remove multiple nodes
- indexOf: return node index
- elementAt: return node by index
- addAt: insert a node in a specific place (by index)
- removeAt: remove a specific node (by index)
function Node(element) {
this.element = element
this.next = null
}
function LinkedList() {
let length = 0
let head = null
this.size = function() {
return length
}
this.head = function() {
return head
}
this.add = function(element) {
let node = new Node(element)
if (head === null) {
head = node
} else {
let currentNode = head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = node
}
length++
}
this.remove = function(element) {
let currentNode = head
let previousNode
if (currentNode.element !== element) {
head = currentNode.next
} else {
while (currentNode.element !== element) {
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
}
this.isEmpty = function() {
return length === 0
}
this.indexOf = function(element) {
let currentNode = head
let index = -1
while (currentNode) {
index++
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
}
return -1
}
this.elementAt = function(index) {
let currentNode = head
let count = 0
while (count < index) {
count++
currentNode = currentNode.next
}
return currentNode.element
}
this.addAt = function(index, element) {
let node = new Node(element)
let currentNode = head
let previousNode
let currentIndex = 0
if (index > length) return false
if (index === 0) {
node.next = currentNode
head = node
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
node.next = currentNode
previousNode.next = node
}
length++
}
this.removeAt = function(index) {
let currentNode = head
let previousNode
let currentIndex = 0
if (index < 0 || index >= length) return null
if (index === 0) {
head = currentIndex.next
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
return currentNode.element
}
}
4. Collection (of values) (Set)
A collection (many) is one of the basic concepts of mathematics: a set of well-defined and isolated objects. ES6 introduced a collection that bears some resemblance to an array. However, the collection does not allow the inclusion of duplicate elements and does not contain indexes.The standard collection has the following methods:- values: return all items in the collection
- size: return the number of elements
- has: check if an item is in the collection
- add: add item
- remove: remove an item
- union: return the intersection area of two collections
- difference: return the differences between the two collections
- subset: check if one collection is a subset of another
function MySet() {
let collection = []
this.has = function(element) {
return (collection.indexOf(element) !== -1)
}
this.values = function() {
return collection
}
this.size = function() {
return collection.length
}
this.add = function(element) {
if (!this.has(element)) {
collection.push(element)
return true
}
return false
}
this.remove = function(element) {
if (this.has(element)) {
index = collection.indexOf(element)
collection.splice(index, 1)
return true
}
return false
}
this.union = function(otherSet) {
let unionSet = new MySet()
let firstSet = this.values()
let secondSet = otherSet.values()
firstSet.forEach(i => unionSet.add(i))
secondSet.forEach(i => unionSet.add(i))
}
this.intersection = function(otherSet) {
let intersectionSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (otherSet.has(e)) {
intersectionSet.add(e)
}
})
return intersectionSet
}
this.difference = function(otherSet) {
let differenceSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (!otherSet.has(e)) {
differenceSet.add(e)
}
})
return differenceSet
}
this.subset = function(otherSet) {
lat firstSet = this.values()
return firstSet.every(value => otherSet.has(value))
}
}
5. Hash Table (Hash Table)
A hash table is a data structure that is built on a key-value basis. Due to the high speed of searching for values by key, it is used in such structures as Map, Dictionary and Object. As shown in the figure, the hash table has a hash function that converts keys to a list of numbers that are used as the names (values) of keys. The key value search time can reach O (1). Identical keys must return the same value - this is the essence of the hash function.A hash table has the following methods:- add: add a key / value pair
- remove: remove a pair
- lookup: find value by key
function hash(string, max) {
let hash = 0
for (let i = 0; i < string.length; i++) {
hash += string.charCodeAt(i)
}
return hash % max
}
function HashTable() {
let storage = []
const storageLimit = 4
this.add = function(key, value) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
storage[index] = [
[key, value]
]
} else {
let inserted = false
for (let i = 0; i < storage[index].len; i++) {
if (storage[index][i][0] === key) {
storage[index][i][1] = value
inserted = true
}
}
if (inserted === false) {
storage[index].push([key, value])
}
}
}
this.remove = function(key) {
let index = hash(key, storageLimit)
if (storage[index].length === 1 && storage[index][0][0] === key) {
delete storage[index]
} else {
for (let i = 0; i < storage[index]; i++) {
if (storage[index][i][0] === key) {
delete storage[index][i]
}
}
}
}
this.lookup = function(key) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
return undefined
} else {
for (let i = 0; i < storage[index].length; i++) {
if (storage[index][i][0] === key) {
return storage[index][i][1]
}
}
}
}
}
6. Tree
A tree structure is a multilayer (multi-level) structure. It is also a nonlinear structure, unlike an array, stack, and queue. This structure is very effective in terms of adding and searching for elements. Here are some concepts of tree structure:- root: root element, has no parent
- parent node: a direct node of the top layer (level), there can be only one
- child node: direct node (s) of the lower level, there may be several
- siblings: children of one parent node
- leaf: knot without "children"
- Edge: branch or link (link) between nodes
- Path: path (set of links) from the start node to the target element
- Height of Tree: the number of links of the longest path from a specific element to a node that does not have children
- Depth of Node: The number of links from the root node to a specific element.
- Degree of Node: Number of Descendants
Here is an example of a binary search tree (BST). Each node has only two descendants, the left (child) node is smaller than the current (parent) node, the right one is larger: The
methods of this tree are as follows:- add: add node
- findMin: get minimum node
- findMax: get maximum node
- find: find a specific node
- isPresent: check for a specific node
- remove: remove the node
class Node {
constructor(data, left = null, right = null) {
this.data = data
this.left = left
this.right = right
}
}
class BST {
constructor() {
this.root = null
}
add(data) {
const node = this.root
if (node === null) {
this.root = new Node(data)
return
} else {
const searchTree = function(node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data)
return
} else if (node.left !== null) {
return searchTree(node.left)
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data)
return
} else if (node.right !== null) {
return searchTree(node.right)
}
} else {
return null
}
}
return searchTree(node)
}
}
findMin() {
let current = this.root
while (current.left !== null) {
current = current.left
}
return current.data
}
findMax() {
let current = this.root
while (current.right !== null) {
current = current.right
}
return current.data
}
find(data) {
let current = this.root
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right
}
if (current === null) {
return null
}
}
return current
}
isPresent(data) {
let current = this.root
while (current) {
if (data === current.data) {
return true
}
data < current.data ? current = current.left : current = current.right
}
return false
}
remove(data) {
const removeNode = function(node, data) {
if (node === null) return null
if (data === node.data) {
if (node.left === null && node.right === null) return null
if (node.left === null) return node.right
if (node.right === null) return node.left
let tempNode = node.right
while (tempNode.left !== null) {
tempNode = tempNode.left
}
node.data = tempNode.data
node.right = removeNode(node.right, tempNode.data)
return node
} else if (data < node.data) {
node.left = removeNode(node.right, data)
return node
} else {
node.right = removeNode(node.right, data)
return node
}
}
this.root = removeNode(this.root, data)
}
}
Testing:const bst = new BST()
bst.add(4)
bst.add(2)
bst.add(6)
bst.add(1)
bst.add(3)
bst.add(5)
bst.add(7)
bst.remove(4)
console.log(bst.findMin())
console.log(bst.findMax())
bst.remove(7)
console.log(bst.findMax())
console.log(bst.isPresent(4))
Result:1
7
6
false
7. Loaded (prefix) tree (Trie, read as “try”)
The prefix tree is a type of search tree. The data in it is stored sequentially (step by step) - each tree node represents one step. The prefix tree is used in dictionaries, since it significantly speeds up the search.Each tree node is a letter of the alphabet, following a branch leads to the formation of a word. It also contains a “boolean indicator” to determine that the current node is the last letter.The prefix tree has the following methods:- add: add a word to the dictionary
- isWord: check for a word
- print: return all words
function Node() {
this.keys = new Map()
this.end = false
this.setEnd = function() {
this.end = true
}
this.isEnd = function() {
return this.end
}
}
function Trie() {
this.root = new Node()
this.add = function(input, node = this.root) {
if (input.length === 0) {
node.setEnd()
return
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node())
return this.add(input.substr(1), node.key.get(input[0]))
} else {
return this.add(input.substr(1), node.keys.get(input[0]))
}
}
this.isWord = function(word) {
let node = this.root
while (word.length > 1) {
if (node.keys.has(word[0])) {
return false
} else {
node = node.keys.get(word[0])
word = word.substr(1)
}
}
return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false
}
this.print = function() {
let words = new Array()
let search = function(node = this.root, string) {
if (node.keys.size !== 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter))
}
if (node.isEnd()) {
words.push(string)
}
} else {
string.length > 0 ? words.push(string) : undefined
return
}
}
search(this.root, new String())
return words.length > 0 ? words : null
}
}
8. The graph (graph) (Graph)
A graph, also known as a Network, is a collection of interconnected nodes. There are two kinds of graphs - oriented and non-oriented, depending on whether the links have a direction. Graphs are used everywhere, for example, to calculate the best route in navigation applications or to create a list of recommendations on social networks.Graphs can be presented in the form of a list or matrix.List
In this case, all the parent nodes are located on the left, and their children are on the right.
The matrix
In this case, the nodes are distributed in rows and columns, the intersection of the row and column shows the relationship between the nodes: 0 means that the nodes are not connected, 1 - the nodes are connected.
The graph is searched by two methods - breadth-first search (Breath-First-Search, BFS) and depth-deep search (Depth-First-Search, DFS).Consider BFS:function bfs(graph, root) {
let nodesLen = {}
for (let i = 0; i < graph.length; i++) {
nodesLen[i] = Infinity
}
nodesLen[root] = 0
let queue = [root]
let current
while (queue.length !== 0) {
current = queue.shift()
let curConnected = graph[current]
let neighborIdx = []
let idx = curConnected.indexOf(1)
while (idx !== -1) {
neighborIdx.push(idx)
idx = curConnected.indexOf(1, idx + 1)
}
for (let i = 0; i < neighborIdx.length; i++) {
if (nodesLen[neighborIdx[i]] === Infinity) {
nodesLen[neighborIdx[i]] = nodesLen[current] + 1
queue.push(neighborIdx[i])
}
}
}
return nodesLen
}
Testing:let graph = [
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 0, 0]
]
console.log(bfs(graph, 1))
Result:{
0: 2,
1: 0,
2: 1,
3: 3,
4: Infinity
}
That’s all for me. I hope you find something useful for yourself. Happy coding!