Good day.I present to you the translation of the article “Algorithms on Graphs: Let's talk Depth-First Search (DFS) and Breadth-First Search (BFS)” by Try Khov.What is a graph traversal?
In simple words, a graph traversal is a transition from one of its vertices to another in search of the connection properties of these vertices. Links (lines connecting vertices) are called directions, paths, faces, or edges of a graph. The vertices of the graph are also referred to as nodes.The two main graph traversal algorithms are Depth-First Search, DFS and Breadth-First Search, BFS.Despite the fact that both algorithms are used to traverse the graph, they have some differences. Let's start with DFS.Depth Search
DFS follows the concept of “go deep, head first”. The idea is that we move from the starting peak (point, place) in a certain direction (along a certain path) until we reach the end of the path or destination (desired peak). If we have reached the end of the path, but it is not a destination, then we go back (to the point of branching or diverging paths) and go along a different route.Let's look at an example. Suppose we have a directed graph that looks like this:
We are at point “s” and we need to find the vertex “t”. Using DFS, we investigate one of the possible paths, move along it to the end and, if we do not find t, go back and explore another path. Here's what the process looks like:
Here we move along the path (p1) to the nearest peak and see that this is not the end of the path. Therefore, we move on to the next peak.
We reached the end of p1, but did not find t, so we return to s and move along the second path.
Having reached the top of the path “p2” closest to the point “s”, we see three possible directions for further movement. Since we have already visited the peak crowning the first direction, we are moving along the second.
We again reached the end of the path, but did not find t, so we go back. We follow the third path and, finally, we reach the desired peak "t".
This is how DFS works. We move along a certain path to the end. If the end of the path is the desired peak, we are done. If not, go back and move on a different path until we explore all the options.We follow this algorithm for every vertex visited.The need for repeated repetition of the procedure indicates the need to use recursion to implement the algorithm.Here is the JavaScript code:
function dfs(adj, v, t) {
if(v === t) return true
if(v.visited) return false
v.visited = true
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
let reached = dfs(adj, neighbor, t)
if(reached) return true
}
}
return false
}
Note: This special DFS algorithm allows you to check whether it is possible to get from one place to another. DFS can be used for various purposes. These goals will determine how the algorithm itself will look. However, the general concept looks exactly like that.DFS Analysis
Let's analyze this algorithm. Since we go around each “neighbor” of each node, ignoring those that we visited earlier, we have a runtime equal to O (V + E).A brief explanation of what V + E means:V is the total number of vertices. E is the total number of faces (edges).It might seem more appropriate to use V * E, but let's think about what V * E means.V * E means that with respect to each vertex, we must investigate all the faces of the graph regardless of whether these faces belong to a particular vertex.On the other hand, V + E means that for each vertex we evaluate only the edges adjacent to it. Returning to the example, each vertex has a certain number of faces and, in the worst case, we go around all the vertices (O (V)) and examine all the faces (O (E)). We have V vertices and E faces, so we get V + E.Further, since we use recursion to traverse each vertex, this means that a stack is used (infinite recursion leads to a stack overflow error). Therefore, the spatial complexity is O (V).Now consider the BFS.Wide search
BFS follows the concept of "expand wide, rising to the height of a bird's flight" ("go wide, bird's eye-view"). Instead of moving along a certain path to the end, BFS involves moving forward one neighbor at a time. This means the following:Instead of following the path, BFS means visiting the neighbors closest to s in a single action (step), then visiting neighbors' neighbors and so on until t is detected.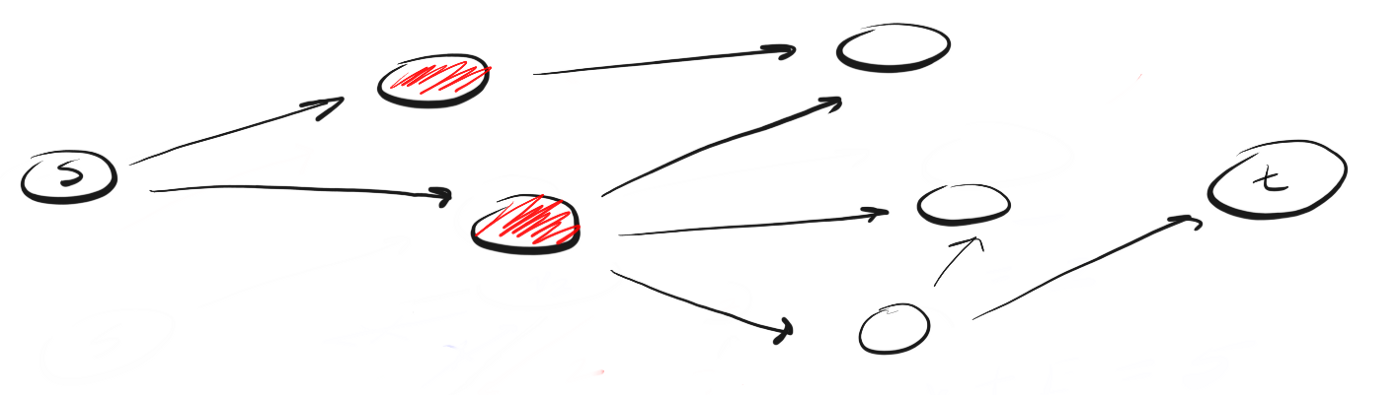
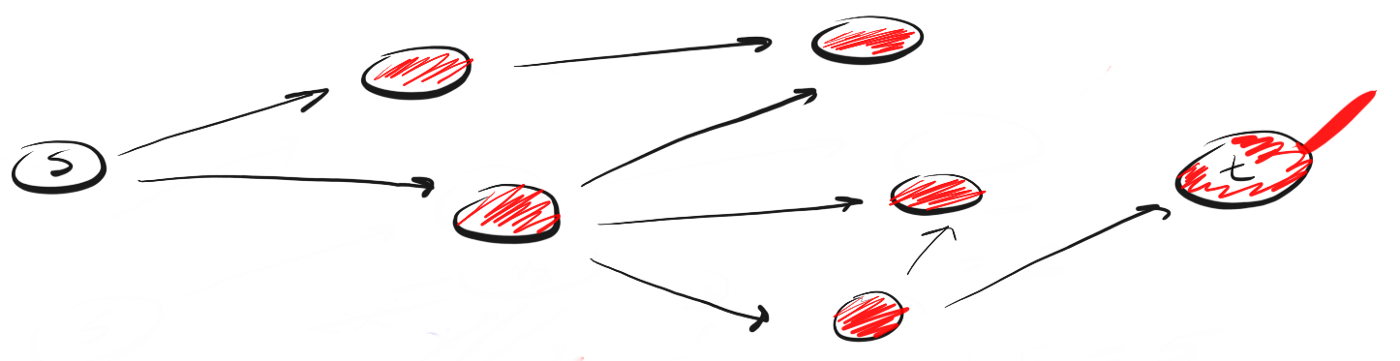How is DFS different from BFS? I like to think that DFS goes ahead, and BFS is not in a hurry, but studies everything within one step.The question then arises: how do you know which neighbors should be visited first?To do this, we can use the concept of "first in, first out" (first-in-first-out, FIFO) from the queue. We queue first the peak closest to us, then its unvisited neighbors, and continue this process until the queue is empty or until we find the vertex we are looking for.Here is the code:
function bfs(adj, s, t) {
let queue = []
queue.push(s)
s.visited = true
while(queue.length > 0) {
let v = queue.shift()
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
queue.push(neighbor)
neighbor.visited = true
if(neighbor === t) return true
}
}
}
return false
}
BFS Analysis
It might seem that BFS is slower. However, if you look closely at the visualizations, you can see that they have the same runtime.A queue involves processing each vertex before reaching a destination. This means that, in the worst case, BFS explores all vertices and faces.Despite the fact that BFS may seem slower, it is actually faster, because when working with large graphs it is found that DFS spends a lot of time following paths that ultimately turn out to be false. BFS is often used to find the shortest path between two peaks.Thus, the BFS runtime is also O (V + E), and since we use a queue containing all the vertices, its spatial complexity is O (V).Real life analogies
If you give analogies from real life, then this is how I imagine the work of DFS and BFS.When I think of DFS, I imagine a mouse in a maze in search of food. In order to get to the target, the mouse is forced to run into a dead end many times, return and move in a different way, and so on, until it finds a way out of the maze or food.
A simplified version looks like this:
In turn, when I think about BFS, I imagine circles on the water. The fall of a stone into water leads to the spread of disturbances (circles) in all directions from the center.
A simplified version looks like this:
findings
- Depth and breadth searches are used to traverse the graph.
- DFS moves along the edges back and forth, and BFS spreads across neighbors in search of a target.
- DFS uses the stack, and BFS the queue.
- The runtime of both is O (V + E), and the spatial complexity is O (V).
- These algorithms have a different philosophy, but are equally important for working with graphs.
Note Per .: I am not a specialist in algorithms and data structures, therefore, if errors, inaccuracies or incorrect formulations are found, please write in a personal letter for correction and clarification. I will be grateful.Thank you for attention.