💞 ▫️ 💊 简单的图形遍历：以JavaScript为例的深度和广度优先搜索 ☺️ ⤵️ 🗻

美好的一天。

我向您介绍Try Khov撰写的文章“图形算法：深度优先搜索（DFS）和广度优先搜索（BFS）”的翻译。

什么是图遍历？

用简单的话来说，图遍历是从一个顶点到另一个顶点的过渡，以寻找这些顶点的连接属性。链接（连接顶点的线）称为图的方向，路径，面或边。图的顶点也称为节点。

两种主要的图遍历算法是深度优先搜索DFS和广度优先搜索BFS。

尽管两种算法都用于遍历图形，但它们还是有一些区别。让我们从DFS开始。

深度搜寻

DFS遵循“深入，先行”的概念。这个想法是，我们从起始峰（点，位置）沿某个方向（沿着特定路径）移动，直到到达路径或目的地的终点（所需峰）。如果我们已到达路径的尽头，但不是目的地，那么我们将返回（到达分支或分支路径的点）并沿着另一条路线走。

让我们看一个例子。假设我们有一个有向图，如下所示：

我们在点“ s”上，我们需要找到顶点“ t”。使用DFS，我们研究了其中一种可能的路径，一直沿其移动到终点，如果找不到t，则返回并探索另一条路径。流程如下所示：

在这里，我们沿着路径（p1）移动到最近的峰值，并看到这不是路径的终点。因此，我们进入下一个高峰。

我们到达了p1的尽头，但是没有找到t，所以我们回到s并沿着第二条路径移动。

到达最接近点“ s”的路径“ p2”的顶部之后，我们看到了三个可能进一步运动的方向。由于我们已经到达了第一个方向的山峰，因此我们沿着第二个方向移动。

我们再次到达路径的尽头，但没有找到t，因此我们返回。我们遵循第三条路径，最后达到所需的峰值“ t”。

这就是DFS的工作方式。我们沿着一定的道路前进到终点。如果路径的末端是所需的峰，则完成。如果没有，请返回并选择其他路径，直到我们探索所有选项为止。

对于每个访问的顶点，我们都遵循此算法。

需要重复重复该过程表明需要使用递归来实现算法。

这是JavaScript代码：

//  ,       
// , : adj = {A: [B,C], B:[D,F], ... }
function dfs(adj, v, t) {
	// adj -  
	// v -   ()
	// t -  

	//   
	//    ,    
	if(v === t) return true
	if(v.visited) return false

	//    
	v.visited = true
	//    (  ) v
	for(let neighbor of adj[v]) {
		//    
		if(!neighbor.visited) {
			//     ,      
			let reached = dfs(adj, neighbor, t)
			//  true,  
			if(reached) return true
		}
	}
	//   v  t  
	return false
}

注意：这种特殊的DFS算法允许您检查是否可以从一个地方到达另一个地方。DFS可以用于各种目的。这些目标将确定算法本身的外观。但是，一般概念看起来完全像那样。

DFS分析

让我们分析一下这种算法。由于我们绕过每个节点的每个“邻居”，而忽略了我们先前访问的节点，因此运行时等于O（V + E）。

V + E的含义的简要说明：

V是顶点的总数。 E是面（边缘）的总数。

使用V * E似乎更合适，但让我们考虑一下V * E的含义。

V * E表示对于每个顶点，我们必须研究图形的所有面，而不管这些面是否属于特定的顶点。

另一方面，V + E表示对于每个顶点，我们仅评估与其相邻的边。回到示例，每个顶点都有一定数量的面，在最坏的情况下，我们绕过所有顶点（O（V））并检查所有面（O（E））。我们有V个顶点和E个面，所以我们得到V +E。

此外，由于我们使用递归遍历每个顶点，因此这意味着使用了堆栈（无限递归会导致堆栈溢出错误）。因此，空间复杂度为O（V）。

现在考虑BFS。

广泛搜索

BFS遵循“扩大范围，达到鸟类飞行的高度”的概念（“扩大范围，鸟瞰”）。 BFS并非每次都向前移动一个邻居，而是沿着某个路径移动到终点。这意味着以下内容：

BFS不是沿着路径运行，而是意味着在单个操作（步骤）中访问最接近s的邻居，然后访问邻居的邻居，依此类推，直到检测到t。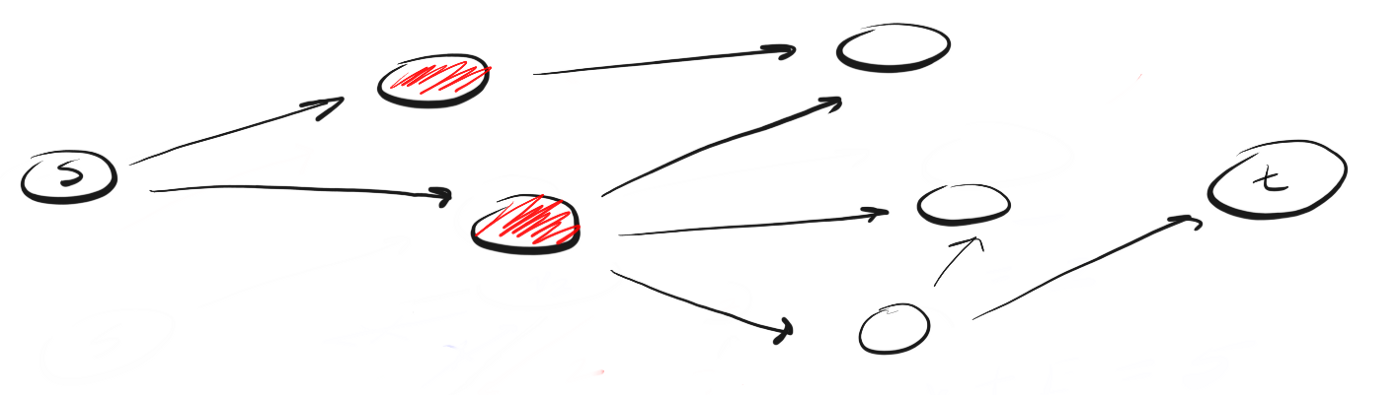

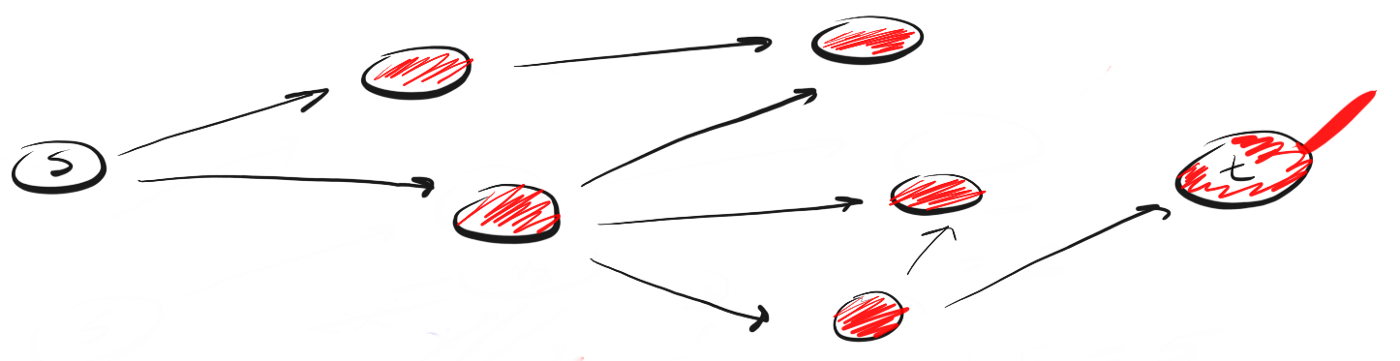DFS与BFS有何不同？我喜欢认为DFS可以继续前进，而BFS并不着急，而是一步一步地研究所有内容。

随之而来的问题是：您如何知道应该首先拜访哪些邻居？

为此，我们可以使用队列中的“先进先出”（先进先出，FIFO）概念。我们首先将最接近我们的峰排队，然后将其未访问的邻居排队，并继续此过程，直到队列为空或找到要寻找的顶点为止。

这是代码：

//  ,       
// , : adj = {A:[B,C,D], B:[E,F], ... }
function bfs(adj, s, t) {
	// adj -  
	// s -  
	// t -  

	//  
	let queue = []
	//  s  
	queue.push(s)
	//  s         
	s.visited = true
	while(queue.length > 0) {
		//   ()   
		let v = queue.shift()
		// abj[v] -  v
		for(let neighbor of adj[v]) {
			//    
			if(!neighbor.visited) {
				//    
				queue.push(neighbor)
				//    
				neighbor.visited = true
				//     ,  
				if(neighbor === t) return true
			}
		} 
	}
	//  t  ,     
	return false
}

BFS分析

看来BFS速度较慢。但是，如果仔细观察这些可视化，您会发现它们具有相同的运行时。

队列涉及在到达目的地之前处理每个顶点。这意味着，在最坏的情况下，BFS会探索所有顶点和面。

尽管事实上BFS似乎较慢，但实际上却更快，因为在处理大型图形时，发现DFS花费大量时间遵循最终被证明是错误的路径。 BFS通常用于查找两个峰之间的最短路径。

因此，BFS运行时也是O（V + E），并且由于我们使用包含所有顶点的队列，因此其空间复杂度为O（V）。