🐸 🙍🏻 👨🏾‍🤝‍👨🏽 扭索饰以不同的方式 🌮 🛄 🌇

扭索状装饰是纸币和其他证券的典型特征。在上一篇文章中可以找到有关它们的详细故事，并涉及历史。那里还给出了一种按点构建断头台的绘图算法。

毫无用处，但要注意的是，我们绘制它们不仅是出于娱乐目的，而且出于实用目的，例如，将那些非常有用的东西添加到设计中。成千上万的点只会减慢编辑器的速度，但无论如何它还是无法显示结果-代替真实的连续线条，会得到某种平均点的结果，就像上帝会赋予灵魂一样。

因此，现在该考虑另一种算法了-该算法将立即给出向量。由于在流行的曲线编辑器中，仅建议使用贝塞尔曲线进行插值，因此我们将重点介绍它们。

实际上，该算法很简单-比第一部分中描述的要简单得多。我们采用两条包络曲线，设置适合360度的波数，估计实际扭索形应从当前点到下一点的角度和曲率，并用四个贝塞尔曲线插值。

这是Asymptote中的一个程序，对于此类事情非常方便。

import graph;

size(1000,1000);
xaxis(ticks=Ticks);
yaxis(ticks=Ticks);

defaultpen(2);

var zero = (0,0);

/////////////////////////////

//         
// 0..180 -> 0..1
real tens(bool at_top, real angle)
{
  return angle/180;
}

guide wave(path top, path bottom, int parts, real offset)
{
  guide w;
  real step = 1/parts;
  real half = step/2;

  pair[] top_pt;
  pair[] bot_pt;

  pair[] top_dir;
  pair[] bot_dir;

  //   
  real[] top_angle;
  real[] bot_angle;

  for(int i: sequence(0,parts-1))
  {
    real rel = i*step + step*offset;

    real top_time = reltime(top, rel);
    real bot_time = reltime(bottom, rel+half);

    //   
    top_pt[i] = point(top, top_time);
    bot_pt[i] = point(bottom, bot_time);

    //       rel
    top_dir[i] = dir(top, top_time);
    bot_dir[i] = dir(bottom, bot_time);
  }

  for(int i: sequence(0,parts-1))
  {
    int prev = i == 0 ? parts-1 : i-1;
    int next = i == parts-1 ? 0 : i+1;

    // t: t[i]--b[i] /\ t[i]--b[prev]

    var v1 = bot_pt[i] - top_pt[i];
    var v2 = bot_pt[prev] - top_pt[i];
    var a = degrees(v2) - degrees(v1);

    top_angle[i] = a<0 ? 360+a : a;

    // b: b[i]--t[i] /\ b[i]--t[next]
    v1 = top_pt[i] - bot_pt[i];
    v2 = top_pt[next] - bot_pt[i];
    a = degrees(v2) - degrees(v1);

    bot_angle[i] = a<0 ? 360+a : a;
  }

  for(int i: sequence(0,parts-1))
  {
    int next = i == parts-1 ? 0 : i+1;

    var l1 = length(top_pt[i]--bot_pt[i]);
    pair ctl1 = top_pt[i] + top_dir[i] * tens(true, top_angle[i]) * l1;
    pair ctl2 = bot_pt[i] - bot_dir[i] * tens(false, bot_angle[i]) * l1;

    w = w .. top_pt[i] .. controls ctl1 and ctl2 .. bot_pt[i];

    var l2 = length(bot_pt[i]--top_pt[next]);
    ctl1 = bot_pt[i] + bot_dir[i] * tens(false, bot_angle[i]) * l2;
    ctl2 = top_pt[next] - top_dir[next] * tens(true, top_angle[next]) * l2;

    w = w .. bot_pt[i] .. controls ctl1 and ctl2 .. top_pt[next];
  }

  return w;
}

//   ,  
void repeat(int count, path top, path bottom, int parts)
{
  real step = 1/count;
  for(int i: sequence(0, count-1))
  {
    draw(wave(top, bottom, parts, step*i));
  }
}

//            
//                
path normalize(path p)
{
  var min = min(p);
  var max = max(p);
  var top_center = min + ((max.x-min.x)/2, (max.y-min.y)/2);
  return scale(20*1/(max-min).x)*shift(zero - top_center)*p;
}

/////////////////////////////

//  3 -   ,     
path top = (338.499521684,-159.274266483)
     ..controls (327.252951684,-158.148796483) and (323.448961684,-145.618286483) .. (318.743661684,-137.260595483)
     ..controls (309.897671684,-123.808725483) and (292.025851684,-123.657732483) .. (278.251471684,-118.807470483)
     ..controls (272.669581684,-117.510629483) and (268.731931684,-109.221757483) .. (274.571781684,-105.645360483)
     ..controls (281.545351684,-101.031122483) and (290.488261684,-97.7906864833) .. (293.317871684,-89.0437964838)
     ..controls (296.611021684,-81.8498064838) and (293.894071684,-73.5853264838) .. (295.556161684,-66.3445764838)
     ..controls (299.563831684,-59.7686064838) and (308.181311684,-64.5344964838) .. (312.903811684,-67.4344264838)
     ..controls (325.368171684,-74.9872364838) and (341.157891684,-80.6126364838) .. (355.257331684,-73.9383264838)
     ..controls (363.506651684,-70.9246164838) and (370.115991684,-63.9703964838) .. (378.731941684,-62.0926264838)
     ..controls (384.688491684,-61.4010364838) and (389.980631684,-67.6129964838) .. (387.306161684,-73.3211464838)
     ..controls (385.256921684,-82.8346964838) and (388.441441684,-93.9447564833) .. (397.757331684,-98.3016064833)
     ..controls (403.144721684,-101.085582483) and (412.671611684,-104.606352483) .. (410.331551684,-112.414892483)
     ..controls (406.654931684,-119.718595483) and (396.921641684,-119.937732483) .. (390.144051684,-122.524267483) 
     ..controls (378.065751684,-125.483516483) and (364.313841684,-130.717262483) .. (359.884541684,-143.562216483)
     ..controls (356.731021684,-151.157386483) and (350.818391684,-160.192046483) .. (341.435061684,-159.293796483)
     ..controls (340.456461684,-159.306096483) and (339.478031684,-159.281196483) .. (338.499521684,-159.274296483)
    --cycle;

top = normalize(top);
bottom = scale(0.5)*top;

//  2 -  
top = ellipse(zero, 4, 6);
bottom = ellipse(zero, 2, 3);

//   1,  ,   

top = circle(zero, 5);
bottom = circle(zero, 3);

// 12 ,      8 
// top -  , bottom - 
repeat(12, top, bottom, 8);

//   
//draw(top, red);
//draw(bottom, red);

最容易理解的情况是正弦曲线位于两个圆之间。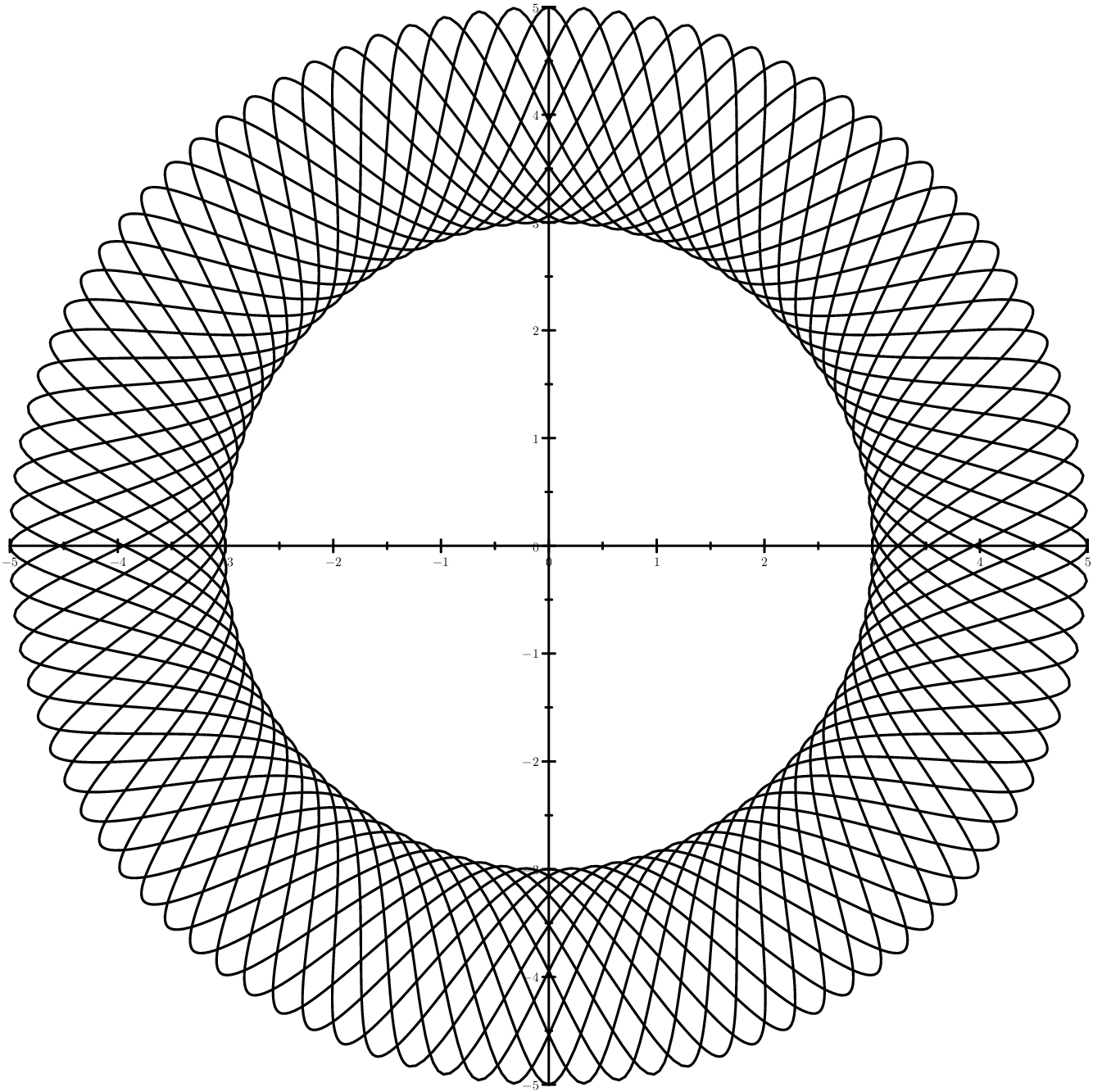

情况更狡猾-椭圆而不是圆圈。

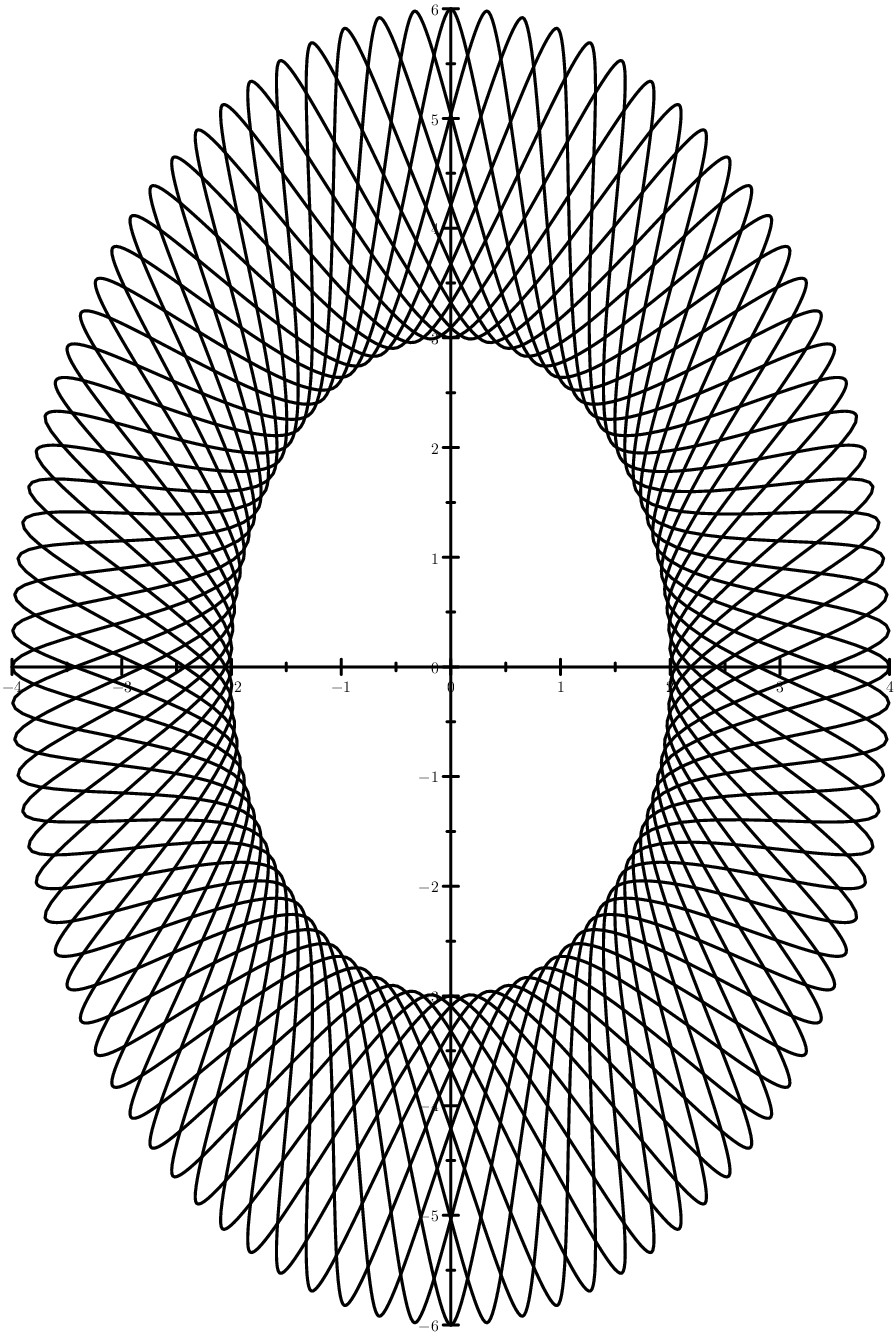和接近工业用途的图片：扭索状装饰，形成了一种艺术气息。

但是，这里的结果并不完美。首先，必须调整tens函数，以使其始终返回0.5的恒定“张力”。其次，曲线不是很对称，在X轴附近的左侧，它们有些混乱。当然，所有这些都可以手动纠正，特别是如果您为国家制造钞票并拥有非常合格的艺术家，但是您可以尝试提高计算的准确性，因为它们显然在信封急剧变化的某些点上误入歧途。

由于断头台是插值的，因此出现了一个问题：它们是否与“真实的”（即由点画出的）相吻合？作为微分几何的新手，我很难说，而是“不”而不是“是”。

但是谁真正看到了差异？

而且不可否认的是，它的实际好处是-拥有数十条Bezier曲线，比起一千个点，它要容易得多，并且它们提供了更多的设计可能性。

另外，该算法也可以得到改进。有两种选择可以立即表明自己：

a）在外部和内部曲线上指定不同数量的点，然后将不会产生将图案磨得更靠近中心的效果，例如在带有圆形和椭圆形的示例中。

b）将点不均匀地放在信封上，例如，使它们更频繁，更不频繁地放置，这将为图案增加新的尺寸。

扭索饰以不同的方式

More articles: