集群是一件神奇的事情:它将大量的非结构化数据转换为一组潜在可见的集群,对其进行分析可以使我们得出有关该数据内容的结论。
聚类方法有很多应用。例如,我们对搜索查询进行聚类以提高排名算法的泛化能力:从一组相似查询中计算出的任何统计信息都比为一个单独查询计算出的相同统计信息更可靠。群集使您可以使用很少遇到的公式来提高查询的质量。另一个明显的例子是Yandex.News,它会自动生成新闻报道。
早在2013年,我很幸运地参与了非常复杂的聚类算法的开发。有必要以非常高的质量对成千上万个对象进行群集,并迅速地完成它:在一台机器上花费数十秒。第一步是建立质量评估系统,在本文中我将讨论它。

, , , .
, : , , , /- . , . — .
1.
, . .
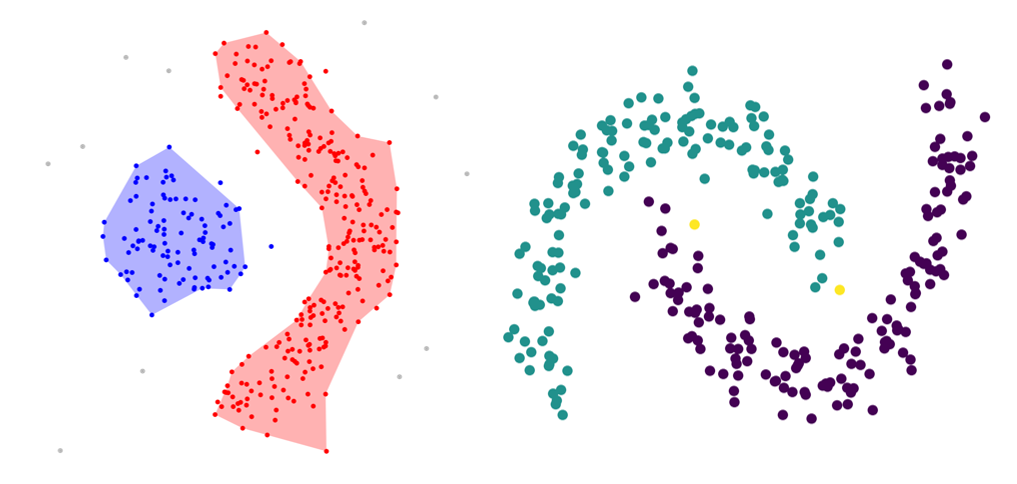
, . Amigo et. al, 2009. A comparison of Extrinsic Clustering Evaluation Metrics based on Formal Constraints , , .
1.1. Cluster Homogeneity,

.
1.2. Cluster Completeness,
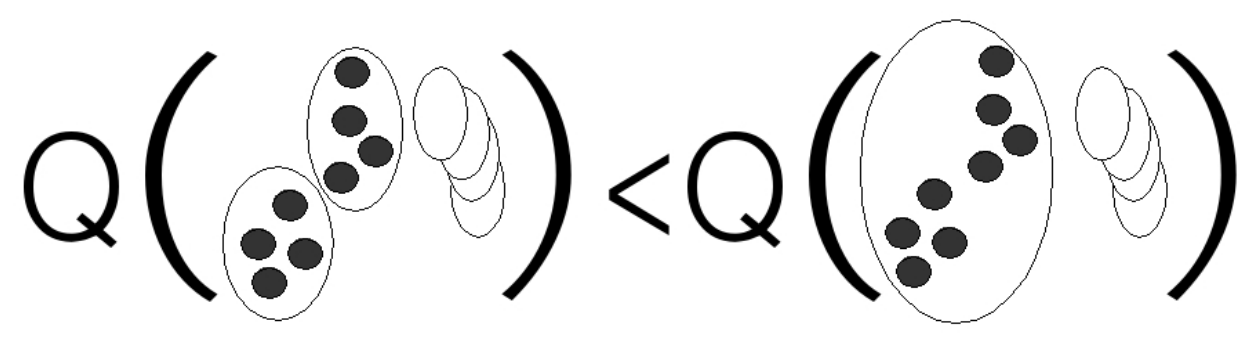
, . .
1.3. Rag Bag
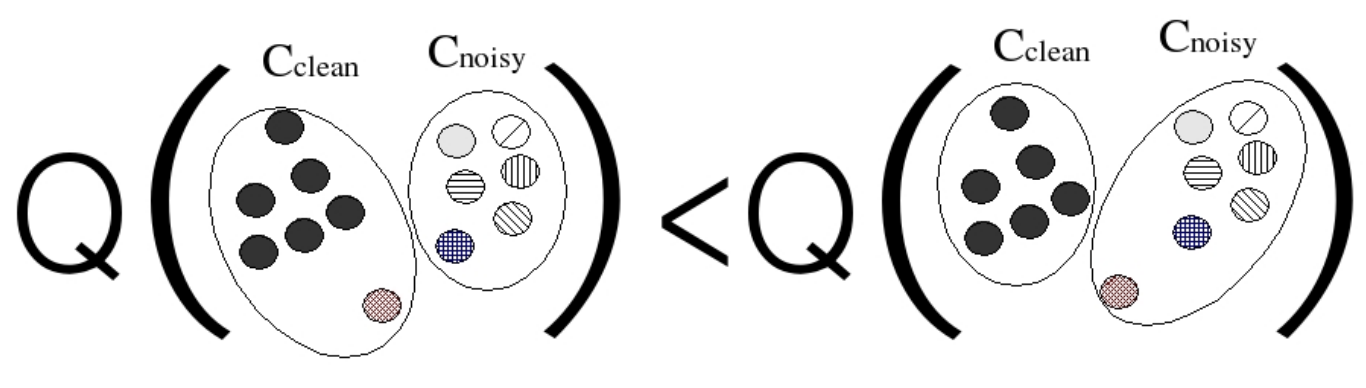
: , , («»), . , , , .
, . , . «» : , .
1.4. Size vs Quantity

.
2.
.
D={d1,...,dN}. . , E⊆2D — ,
∀e1,e2∈E:(e1∩e2≠∅)⇔(e1=e2)
: . , .
, : T={t1,...,tn} C={c1,...,cm}. t(d) c(d) , , , d.
2.1. , ()
. , . , .
. 3 («»), 3 («») 2 («»). : «» , «» «».

8⋅8=64 , :
— 3⋅3+3⋅3+2⋅2=22 ;
— 64−22=42 .
«» «» , - «» .
, :
— TP=18 ;
— FP=6 , ;
— TN=36 ;
— FN=4 , .
, :
P=TP/(TP+FP)=0.75
R=TP/(TP+FN)=0.82
F1=2PRP+R=0.78
, : .
. , : .
pairwise- — . - pairwise- .
2.2. ,
:
P(c,t)=|c∩t||c|
R(c,t)=|c∩t||t|
: «» (y) «» (v). 25 10 . 25/35, — 10/35. . , 30 12 , 25/30, — 10/12.

: , . :
P(c,t)=R(t,c)
F-:
F1(c,t)=2⋅P(c,t)⋅R(c,t)P(c,t)+R(c,t)
. «» , Purity:
Pü[R一世Ťÿ=米∑一世=1个|C一世|米最高1个≤Ĵ≤ñP(C一世,ŤĴ)
, :
一世vË[RsËPü[R一世Ťÿ=ñ∑Ĵ=1个|ŤĴ|ñ最高1个≤一世≤米P(C一世,ŤĴ)
Pü[R一世Ťÿ , . 一世vË[RsËPü[R一世Ťÿ — . , ? , . :
|C2|≈|Ť2|≫|Ť1个|≫|C1个|
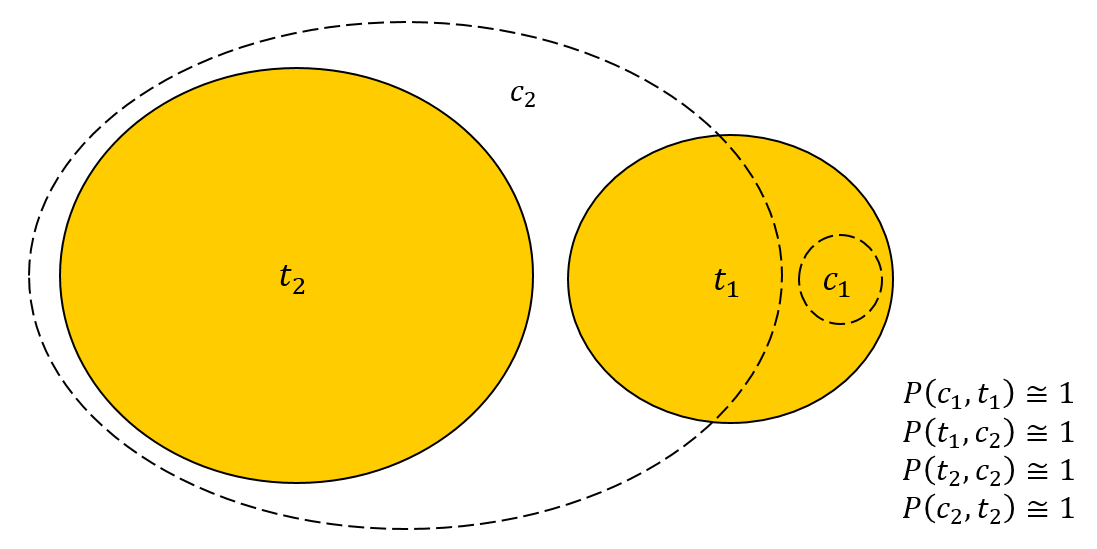
|C2|=1000, |C1个|=2, |Ť1个|=二十, |Ť2|=982. C1个 Ť1个, :
|C1个∩Ť1个|=2,|C1个∩Ť2|=0,
|C2∩Ť1个|=十八,|C2∩Ť2|=982
:
P(C1个,Ť1个)=|C1个∩Ť1个|/|C1个|=2/2=1个
P(C2,Ť2)=|C2∩Ť2|/|C2|=982/1000=0.982
P(Ť1个,C2)=|Ť1个∩C2|/|Ť1个|=十八/二十=0.9
P(Ť2,C2)=|C2∩Ť2|/|Ť2|=982/982=1个
, Purity InversePurity . :
Pü[R一世Ťÿ=0.9982
一世vË[RsËPü[R一世Ťÿ=0.9823
, Ť1个 . , . . Purity Ť1个 C1个, InversePurity — C2. !
F-:
F=ñ∑Ĵ=1个|ŤĴ|ñ最高1个≤一世≤米F(C一世,ŤĴ)
, , . , , , .
2.3. BCubed-
. , . , , ? ?
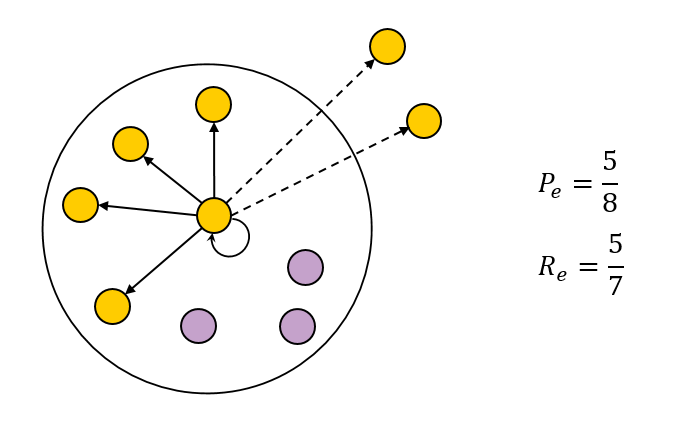
, BCubed- . :
乙CP(d)=|C(d)∩Ť(d)||C(d)|
乙C[R(d)=|C(d)∩Ť(d)||Ť(d)|
:
乙CP=1个ñ∑d∈d乙CP(d)
乙C[R=1个ñ∑d∈d乙C[R(d)
BCubed Precision Cluster Homogeneity Rag Bag, BCubed Recall — Cluster Completeness Size vs Quantity. — F- — :
乙CF=2⋅乙CP⋅乙C[R乙CP+乙C[R
3.
, . , .
, , . d={一个,b,C,d,Ë,F,G,H,一世} , Ť1个={一个,b,C,d,Ë} Ť2={F,G,H,一世} («» «» ).
: C1个={一个,b,C,d,G}, C2={Ë,F,H,一世}.

3.1. BCubed
BCubed- :
乙CP(Ť一世)=1个|Ť一世|∑d∈Ť一世乙CP(d)
乙C[R(Ť一世)=1个|Ť一世|∑d∈Ť一世乙C[R(d)
:
乙CP(一个)=乙CP(b)=乙CP(C)=乙CP(d)=|Ť1个∩C1个||C1个|=0.8,乙CP(Ë)=|Ť1个∩C2||C2|=0.25
乙CP(F)=乙CP(H)=乙CP(一世)=|Ť2∩C2||C2|=0.75,乙CP(G)=|Ť2∩C1个||C1个|=0.2
:
乙CP(Ť1个)=乙CP(一个)+乙CP(b)+乙CP(C)+乙CP(d)+乙CP(Ë)5=4⋅0.8+0.255=0.69
乙CP(Ť2)=乙CP(F)+乙CP(G)+乙CP(H)+乙CP(一世)4=3⋅0.75+0.24=0.6125
:
乙C[R(一个)=乙C[R(b)=乙C[R(C)=乙C[R(d)=|Ť1个∩C1个||Ť1个|=0.8,乙C[R(Ë)=|Ť1个∩C2||Ť1个|=0.2
乙C[R(F)=乙C[R(H)=乙C[R(一世)=|Ť2∩C2||Ť2|=0.75,乙CP(G)=|Ť2∩C1个||Ť2|=0.25
乙C[R(Ť1个)=乙C[R(一个)+乙C[R(b)+乙C[R(C)+乙C[R(d)+乙C[R(Ë)5=4⋅0.8+0.25=0.68
乙C[R(Ť2)=乙C[R(F)+乙C[R(G)+乙C[R(H)+乙C[R(一世)4=3⋅0.75+0.254=0.625
BCP BCR :
乙CP=乙CP(Ť1个)+乙CP(Ť2)2=0.65125
乙C[R=乙C[R(Ť1个)+乙C[R(Ť2)2=0.6525
.
3.2. Expected Cluster Completeness
. , , , , - .
— F- — . , ? .
, , «». . — . : , , .
— :
F:C→Ť
F (cluster completeness):
CCF(Ť)=最高C∈F--1个(Ť)|C∩Ť||Ť|
:
CCF(Ť)=1个Ť∑Ť∈ŤCCF(Ť)
— , F. : .
. , F(C)=Ť,
P(F(C)=Ť)=P(C,Ť)=|C∩Ť||C|
F :
P(F)=∏C∈C|C∩F(C)||C|
:
ËCC(Ť)=∑F:C→ŤP(F)⋅CCF(Ť)
:
ËCC=1个|Ť|∑Ť∈ŤËCC(Ť)
:
ËCC=∑F:C→ŤP(F)⋅CCF(Ť)
. Ť C1个, C2, ..., Cķ, :
|Ť∩C1个|≥|Ť∩C2|≥。。。≥|Ť∩Cķ|
C1个 Ť
P(F(C1个)=Ť)=|C1个∩Ť||C1个|
[R(C1个,Ť)=|C1个∩Ť||Ť|
, , . [R(C1个,Ť).
C1个 , p(C2,Ť) Ť C2. [R(C2,Ť). , ,
P(C1个,Ť)⋅[R(C1个,Ť)+P(C2,Ť)⋅[R(C2,Ť)⋅(1个--P(C1个,Ť))+。。。
ECC . sortedMatchings , , . Precision() Recall() . :
double ExpectedClusterCompleteness(const TMatchings& sortedMatchings) {
double expectedClusterCompleteness = 0.;
double probability = 1.;
for (const TMatching& matching : sortedMatchings) {
expectedClusterCompleteness += matching.Recall() * matching.Precision() * probability;
probability *= 1. - matching.Precision();
}
return expectedClusterCompleteness;
}
, F1个-, !
ECC , 3. Ť1个 C1个, Ť2 — C2. :
ËCC(Ť1个)=[R(C1个,Ť2)⋅P(C1个,Ť1个)+[R(C2,Ť1个)⋅P(C2,Ť1个)⋅(1个--P(C1个,Ť1个))
ËCC(Ť1个)=0.82+0.2⋅0.25⋅(1个--0.8)=0.65
ËCC(Ť2)=[R(C2,Ť2)⋅P(C2,Ť2)+[R(C1个,Ť2)⋅P(C1个,Ť2)⋅(1个--P(C2,Ť2))
ËCC(Ť2)=0.752+0.25⋅0.2⋅(1个--0.75)=0.575
, :
ËCC=ËCC(Ť1个)+ËCC(Ť2)2=0.6125
4.
, 3, C++ MIT GitHub. Linux, Windows.
:
git clone https://github.com/yandex/cluster_metrics/ .
cmake .
cmake --build .
, 3. !
./cluster_metrics samples/sample_markup.tsv samples/sample_clusters.tsv
ECC 0.61250 (0.61250)
BCP 0.65125 (0.65125)
BCR 0.65250 (0.65250)
BCF1 0.65187 (0.65187)
«» , , . , , . , , . — .
5. ,
, , , .
. , , . , , :

: , . , , . , , , — . — ECC!
, , — . .
, , , . .
, , , ECC! ECC - , , , 100% . .
, 1 . : — .

Cluster Completeness
, , . , Cluster Homogeneity, Cluster Completeness, Rag Bag , Size vs Quantity .
, : , , , .
, 3, , .
, , : . , , .