🚠 👿 👼🏿 流行病学模型Covid-19 🍳 🧣 🙅🏽

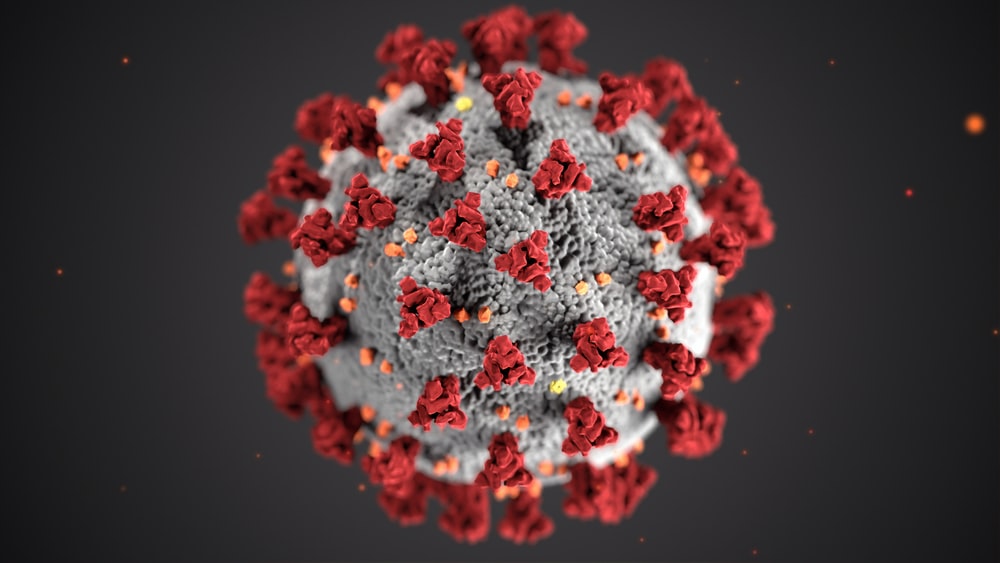
近年来，流行病发展的模式已经非常不同，包括在哈布雷市。这个话题也没有绕过我。我几乎不会在这里写过，但是鉴于我设法找到的东西，发现的依赖关系的重要性及其对我们生活的影响，我不得不分享这个发现。会有很多公式，图表和少量文字。我居住的德国的基本信息和图形。

因此，第一近似的流行病学模型由受感染者的增长公式描述。

不明飞行物护理分钟

大流行的COVID-19是由SARS-CoV-2冠状病毒（2019-nCoV）引起的潜在严重的急性呼吸道感染，已在全球正式宣布。关于Habré的很多信息都涉及此主题-始终记住，它既可靠又有用，反之亦然。

我们敦促您不要批评任何已发布的信息。

官方资料
C
C
()

, .

洗手，照顾亲人，尽可能呆在家里并远程工作。

阅读有关以下内容的出版物：冠状病毒 | 远程工作

N_{t} = N_{0} 2^{t / T_{d}}

$N_t = N_02^{t/T_d}$

哪里

T_{d}

$T_d$ -在几天之内将我们的病例中受感染者加倍的时间，

t

$t$ 天数

N_{0}

$N_0$ 在某个时间点的感染人数，以及

N_{t}

$N_t$ -通过的案件数

t

$t$ 天。如果我们将公式的两个部分除以该地区的总人口，我们将得到相同的公式，只是人口的一部分

P

$P$ 。

P_{t} = P_{0} 2^{t / T_{d}} (1)

$P_t = P_02^{t/T_d} (1)$

该公式的问题在于该公式未考虑到有限的人口和

P

$P$ 很快它将超过1。这在现实生活中不会发生。

流行病学因素决定了病例数可以增加到什么水平。它是根据复制的基本数量计算的。

R_{0}

$R_0$ 。这个数字向我们显示了大约一个感染者感染了多少人，对于每个特定区域而言，这是恒定且特定的，具体取决于该区域的人口密度和其他特征。当没有任何限制因素时，只能在流行开始时确定。公式本身如下所示：

P_{s a t} = 1 - 1 / R_{0}

$P_{sat} = 1 - 1/{R_0}$

还有一个有效的繁殖率

R_{t}

$R_t$ ，这也使我们知道患者感染了多少人。与基数不同，有效数字不断变化。您可以使用上面的公式确定该值，并知道某个时间点的感染数量：

R_{t} = R_{0} (1 - P_{t}) (2)

$R_t = R_0(1 - P_t) (2)$

如果我们采用流行病的简化SEIR ^[1]模型，我们可以找到描述流行病特征的其他因素，例如增长率

G_{r}

$G_r$ 或患者传染时间

D

$D$ 。以下公式显示了数量之间的关系。

G_{r} = \frac{R_{t} - 1}{D}

$G_r = \frac{R_t - 1}{D}$

T_{d} = \frac{l n (2)}{G_{r}}

$T_d = \frac{ln(2)}{G_r}$

使用以上公式，我们可以得出以下依赖性

T_{d} = \frac{D l n (2)}{R_{t} - 1}

$T_d = \frac{D ln(2)}{R_t - 1}$

并将其代入（1），我们得到：

P_{t} = P_{0} 2^{\frac{t (R_{t} - 1)}{D l n (2)}}

$P_t = P_0 2^\frac{t (R_t - 1)}{D ln(2)}$

或简化后

P_{t} = P_{0} e^{\frac{t (R_{t} - 1)}{D}}

$P_t = P_0 e^\frac{t (R_t - 1)}{D}$

如果我们需要在第二天确定值，那么

t = 1

$t = 1$

P_{1} = P_{0} e^{\frac{R_{t} - 1}{D}}

$P_1 = P_0 e^\frac{R_t - 1}{D}$

特定时间的有效复制数量

c u r r e n t

$current$ 可以从公式（2）计算出来，然后只知道复制的基本数量

R_{0}

$R_0$ 以及目前的感染人数

P_{c u r r e n t}

$P_{current}$ 我们可以轻松计算出第二天感染者的百分比。

P_{n e x t} = P_{c u r r e n t} e^{\frac{R_{0} (1 - P_{c u r r e n t}) - 1}{D}}

$P_{next} = P_{current} e^\frac{R_0 (1 - P_{current}) - 1}{D}$

此公式中只有一个参数

R_{0}

$R_0$ ，可以从流行开始时的倍增时间计算得出。举个例子

P_{c u r r e n t} = 0, 0001

$P_{current} = 0,0001$ 并采取n步，我们将在n天内获得一种流行病学状态。时间，曲线的形状，饱和度值，在某个时间点的病例数和其他参数从公式“跳出鼻烟壶的魔鬼”中跳出来。

隔离和其他影响流行病过程的因素如何处理？

所采取的每项措施均以一定的因子（因子）校正复制的基本数量

μ \in [0; 1]

$μ ∈ [0;1]$ 通过以下方式：

P_{n e x t} = P_{c u r r e n t} e^{\frac{μ R_{0} (1 - P_{c u r r e n t}) - 1}{D}}

$P_{next} = P_{current} e^\frac{μ R_0 (1 - P_{current}) - 1}{D}$

为简单起见，您甚至可以定义一个“极限”基本复制编号：

R_{0}^{'} = μ R_{0}

$R'_0 = μ R_0$

此外，在某些时间点，您可以简单地用一个复制号替换另一个复制号，从而调整流行的范围。在一定时期内，这种流行病继续以新病传播，直到发生新的变化为止。更改点或干预点取决于外部因素，例如隔离，学校关闭或需要戴口罩。通常，无法预先知道暴露于这些因素的时间和程度。但是，如果知道校正数变化的值

μ

$μ$ ，它确定了隔离的有效性，您可以了解到隔离的取消将在将来的某个特定时间点受到影响。这为该模型提供了良好的预测机会。这也是在实践中测试其有效性的一种方法。

作为患者的传染时间

D

$D$ 对于Covid-19，取值为10 ^[2]。

模型中没有其他参数，也没有其他自由度。

验证呢？

图表基于德国的数据。

有只有3介入点如下表所示：

而导致以下结果。

在有效复制数量变化的图表上可以看到干预点和模型数据与从公共数据中提取的实际值的比较。

数据的一致性和模型的质量可以在回归图表上进行检查：

德国的模型和计算结果发布在GitHub上。不仅有这些数据，而且还有死亡的研究。

更新：
进行了其他检查。每个国家都有自己的校正因子。

俄罗斯：

意大利：

美国：

更新2：
在GitHub上添加了一个“简单”版本，删除了所有不必要的版本，您可以插入其他国家的值，更改干预点和校正因子。相同的校正因子很可能是被诊断出的感染者与被感染者的比率。但是需要检查。流行病的进一步发展和完成将证实或驳斥这一假说。

在图中，检测到的病例的值以％为单位，并且这些值未针对比率值（校正因子）进行校正。除以该数字，我们得到了检出病例的实际百分比和感染的预后。在简单版本中，已进行了此更正。

参考文献
[1] JM Heffernan等。基本生殖比率的观点。doi.org/10.1098/rsif.2005.0042 JR Soc。界面2005，2，281-293（2005）

[2]何希，Eric HY Lau等。病毒脱落和COVID-19传播能力的时间动态。www.nature.com/articles/s41591-020-0869-5自然（2020）

流行病学模型Covid-19

不明飞行物护理分钟

我们敦促您不要批评任何已发布的信息。

More articles: