背景
最近,在教育活动的框架中,我需要使用良好的旧遗传算法来找到两个变量的最小和最大函数。但是,令我惊讶的是,互联网上在python上没有类似的实现,并且有关遗传算法的Wikipedia文章也没有涵盖这一部分。 因此,我决定用Python编写可视化算法的小型程序包,根据该可视化程序,可以方便地配置此算法并查找所选模型的精妙之处。在这篇简短的文章中,我想分享过程,观察和结果。
因此,我决定用Python编写可视化算法的小型程序包,根据该可视化程序,可以方便地配置此算法并查找所选模型的精妙之处。在这篇简短的文章中,我想分享过程,观察和结果。算法原理
我不会谈论遗传算法工作的全局原理,但是如果您还没有听说过,那么可以在Wikipedia上熟悉它。目前,该程序包仅实现一个GA,该GA由输入数据通过简单的Guiche参数化。我将简要介绍所选的遗传函数和基本算法解决方案。单染色体个体在其每个基因中携带有关相应x或y坐标的信息。人口由许多个人决定,但该人口被分为4个人。当然,该解决方案是由于试图避免收敛到局部最优,因为任务是寻找全局极值。如实践所示,这种划分在许多情况下不允许一种基因型在整个人群中占主导地位,相反,却赋予“进化”更大的动力。对于人口中的每个这样的部分,将应用以下算法:- 选择与排名方法相似。选择具有最佳适应度功能指标的3个人(即,按照用户设置的功能的升序/降序对个人进行分类,这是适应功能)。
- 接下来,以这样的方式应用交叉功能,即新一代(或者更确切地说是4个人的新群体)从具有更好适应性功能指示的一个人那里接收2对未突变基因,并从另外两个人那里获得一对突变基因。下一节将详细介绍变异函数的编译。
选择,杂交和突变的操作原理在外观上看起来像这样(在N代中,个体的染色体已经按照正确的顺序进行了排序,黑色小方块表示突变):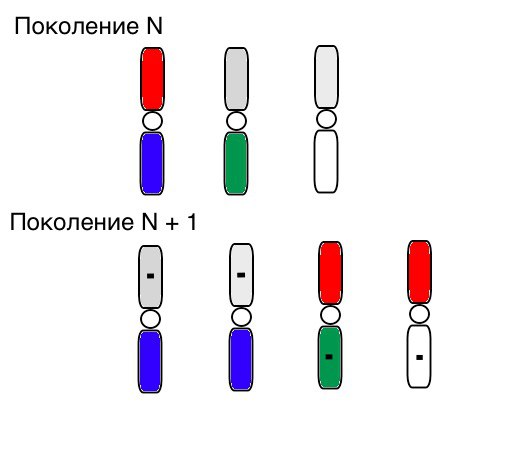
初步测试和观察
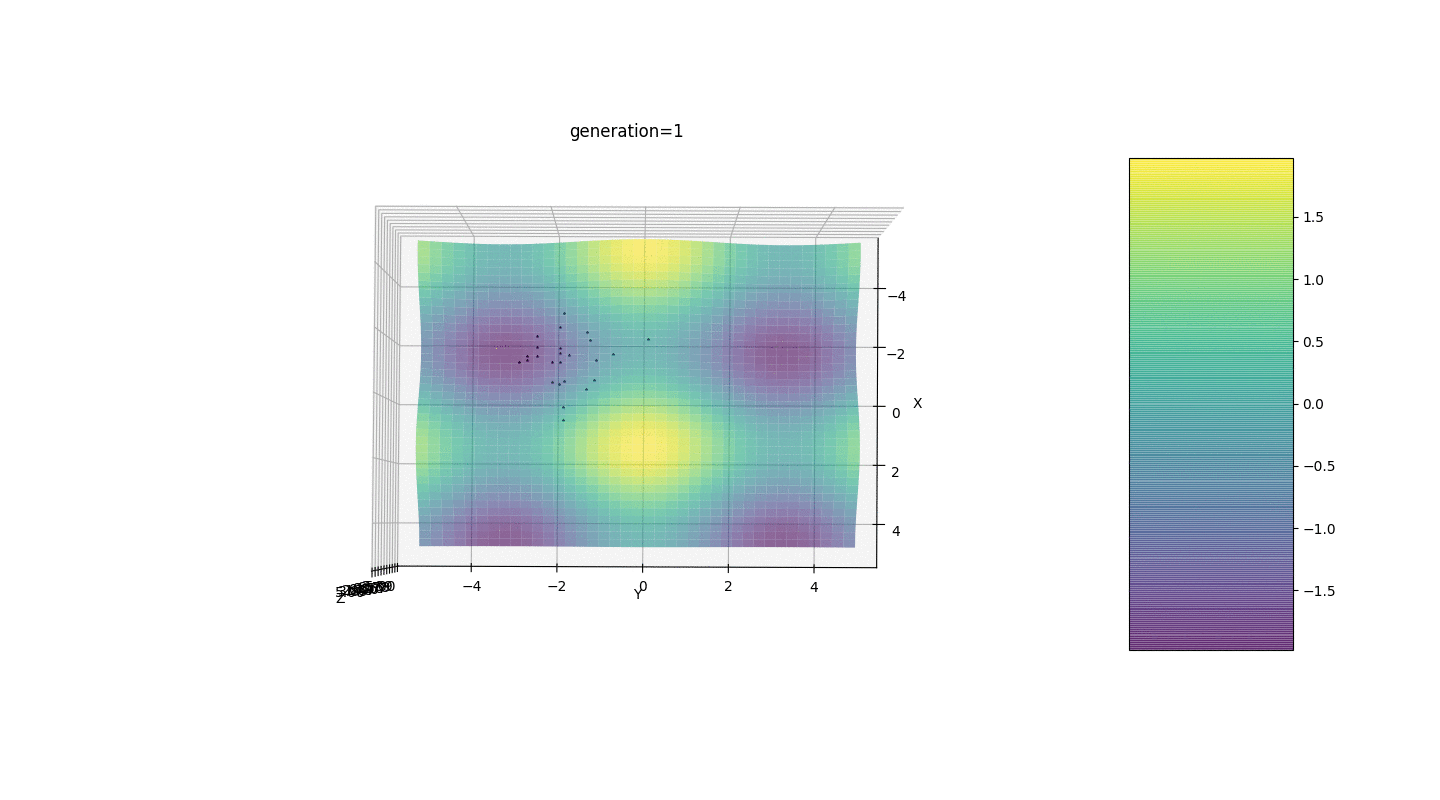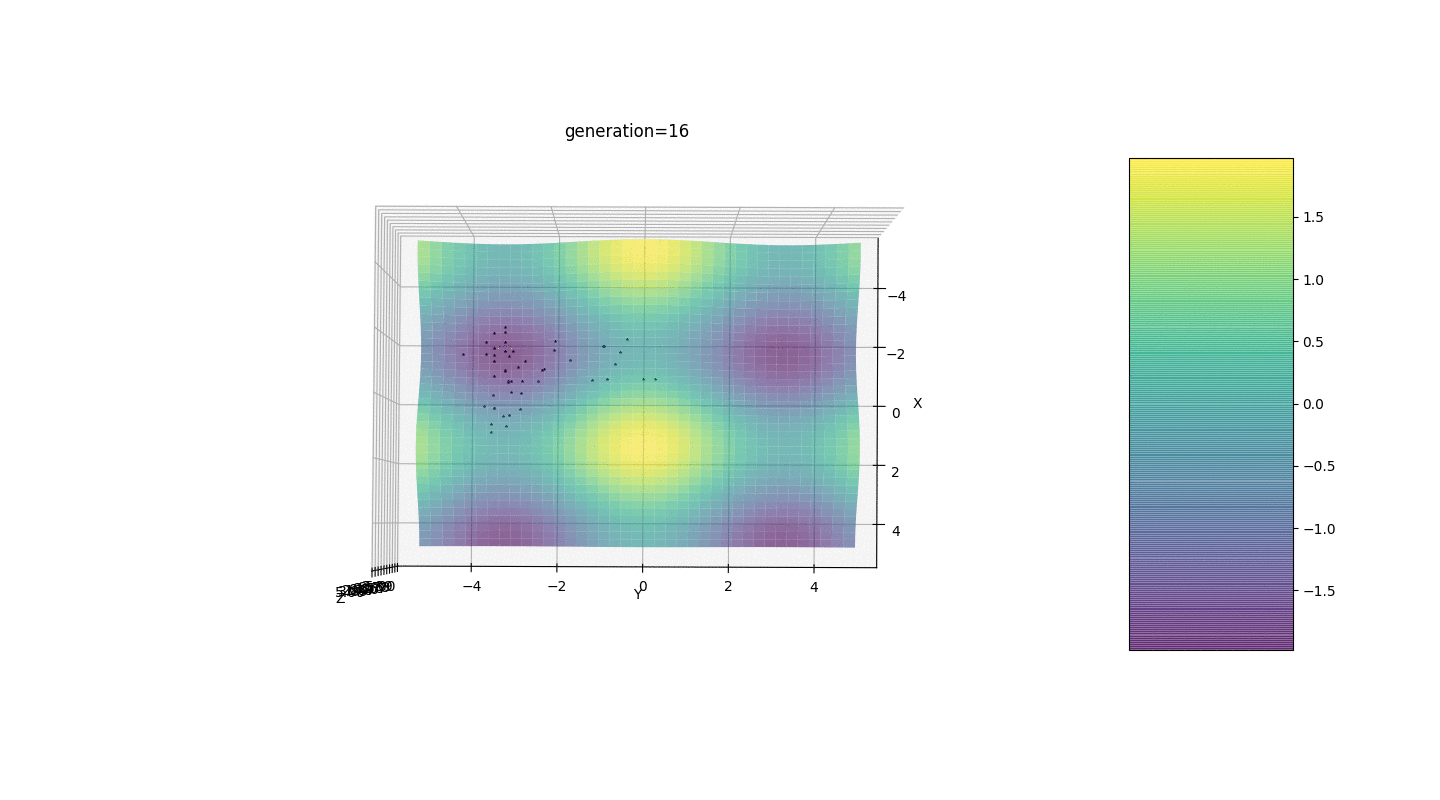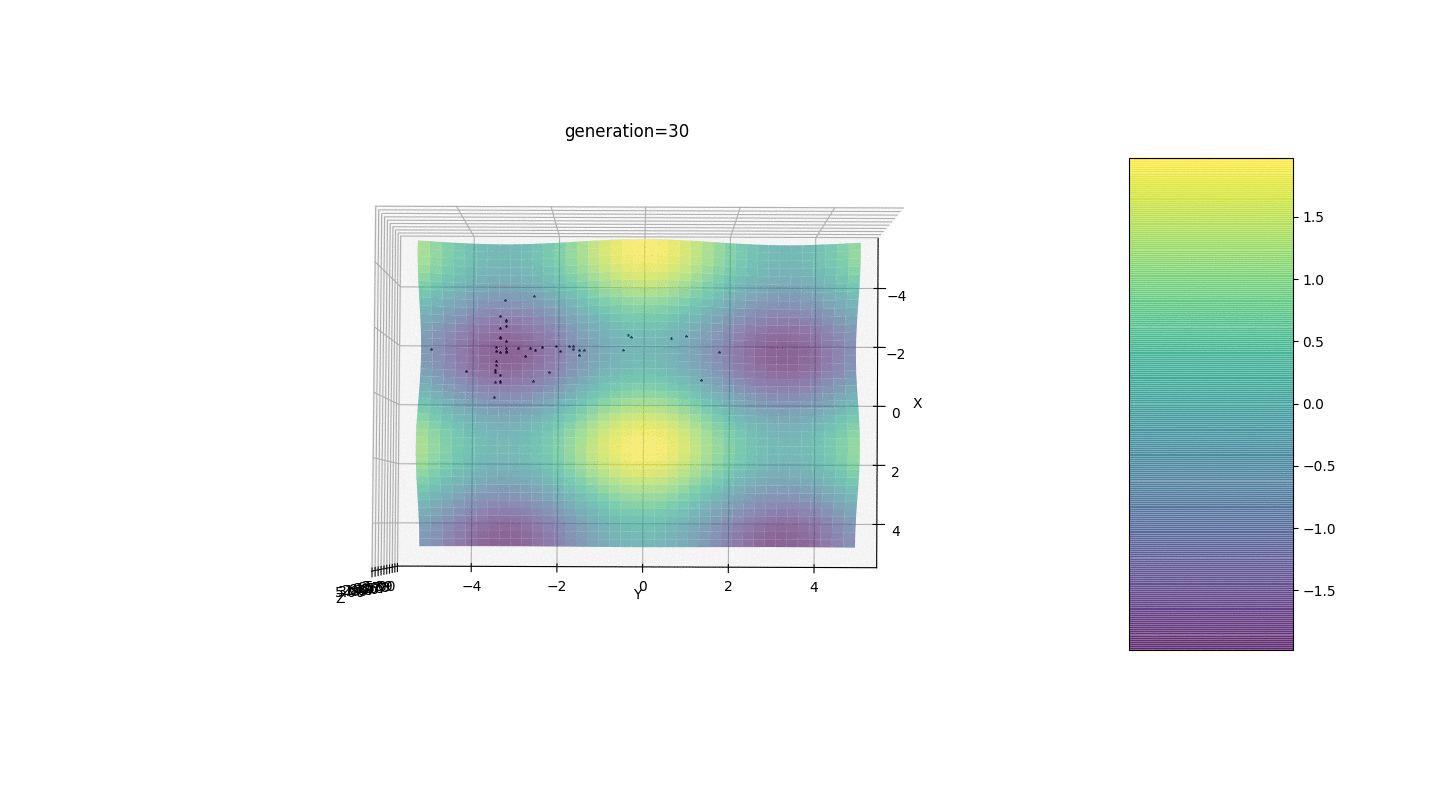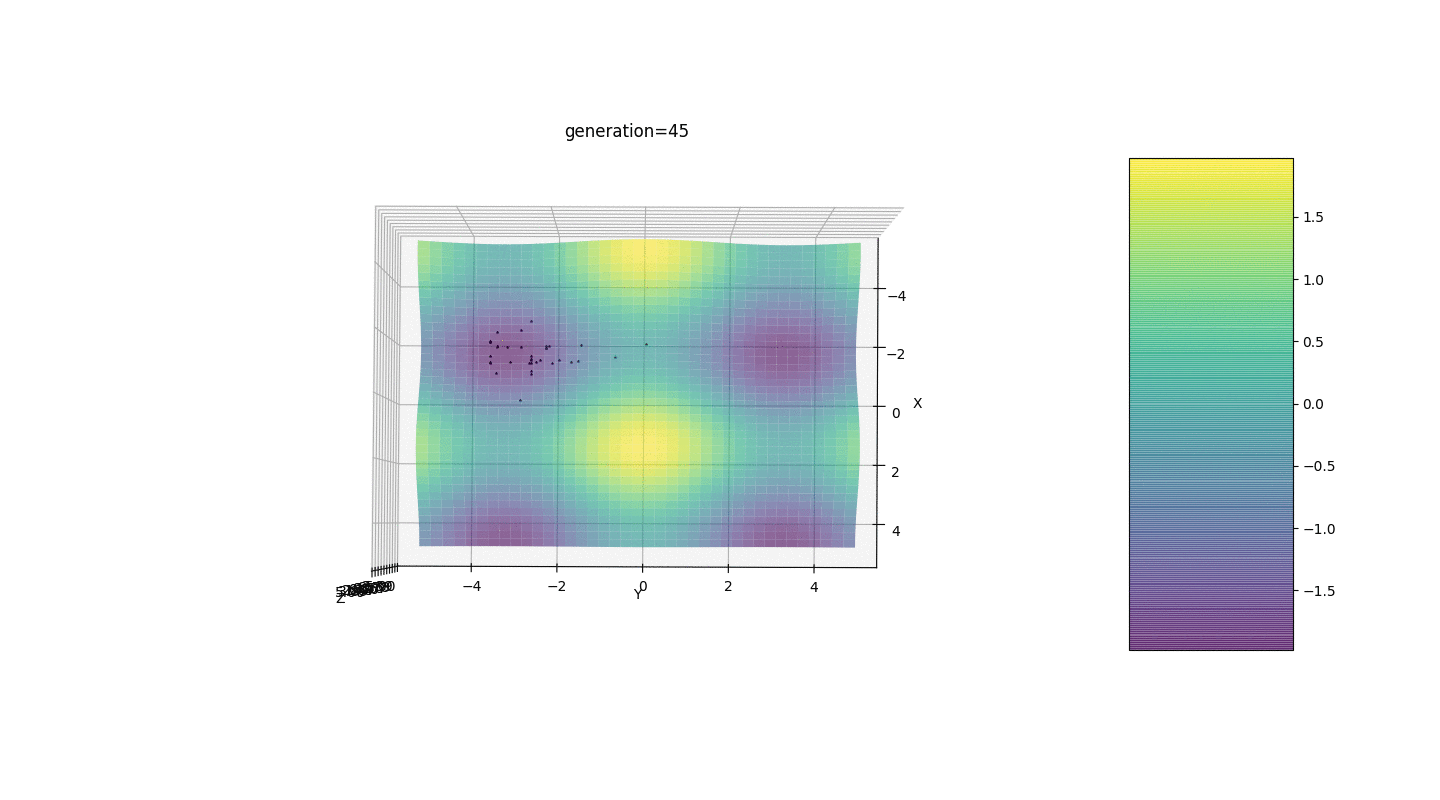
因此,我们在两个简单的示例上测试该算法:测试1
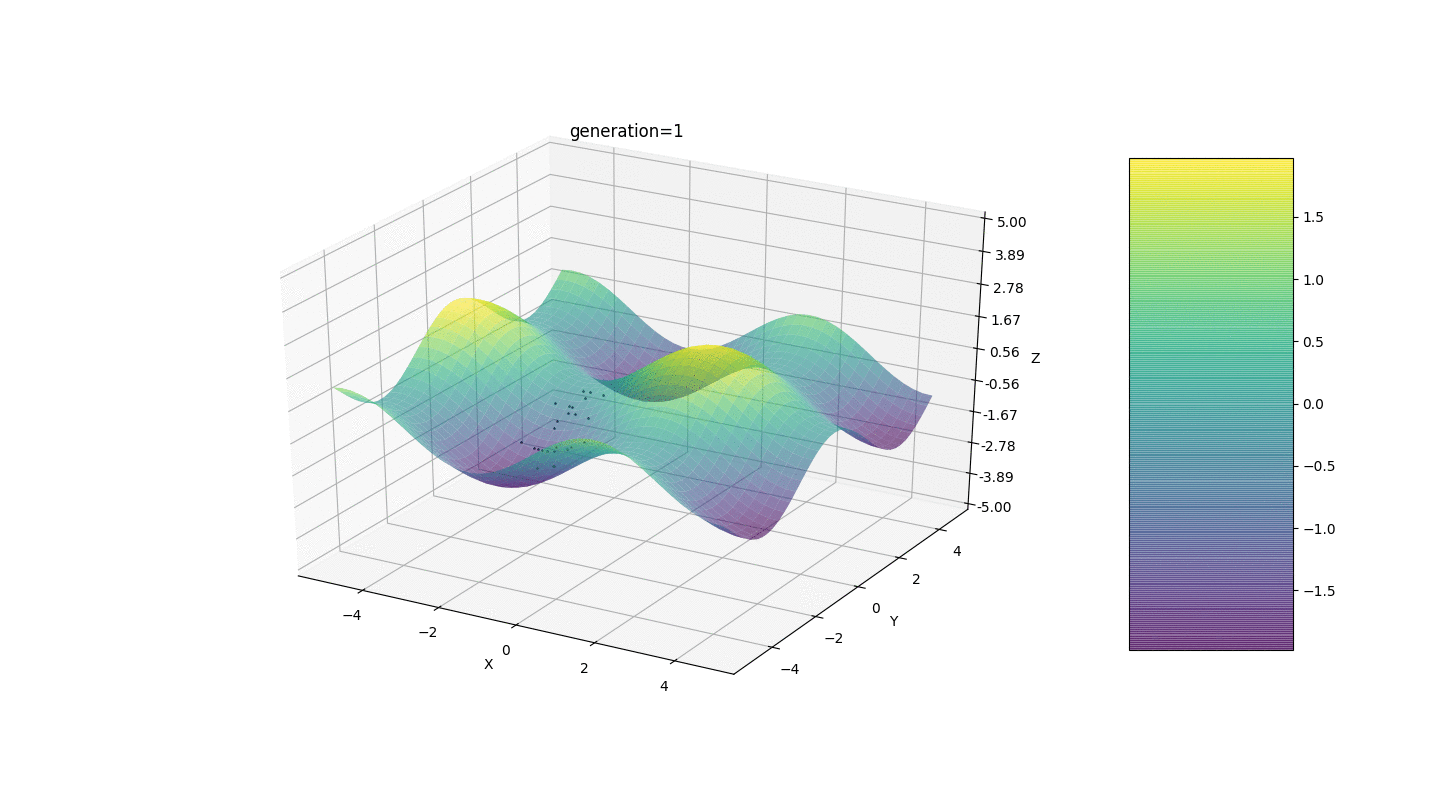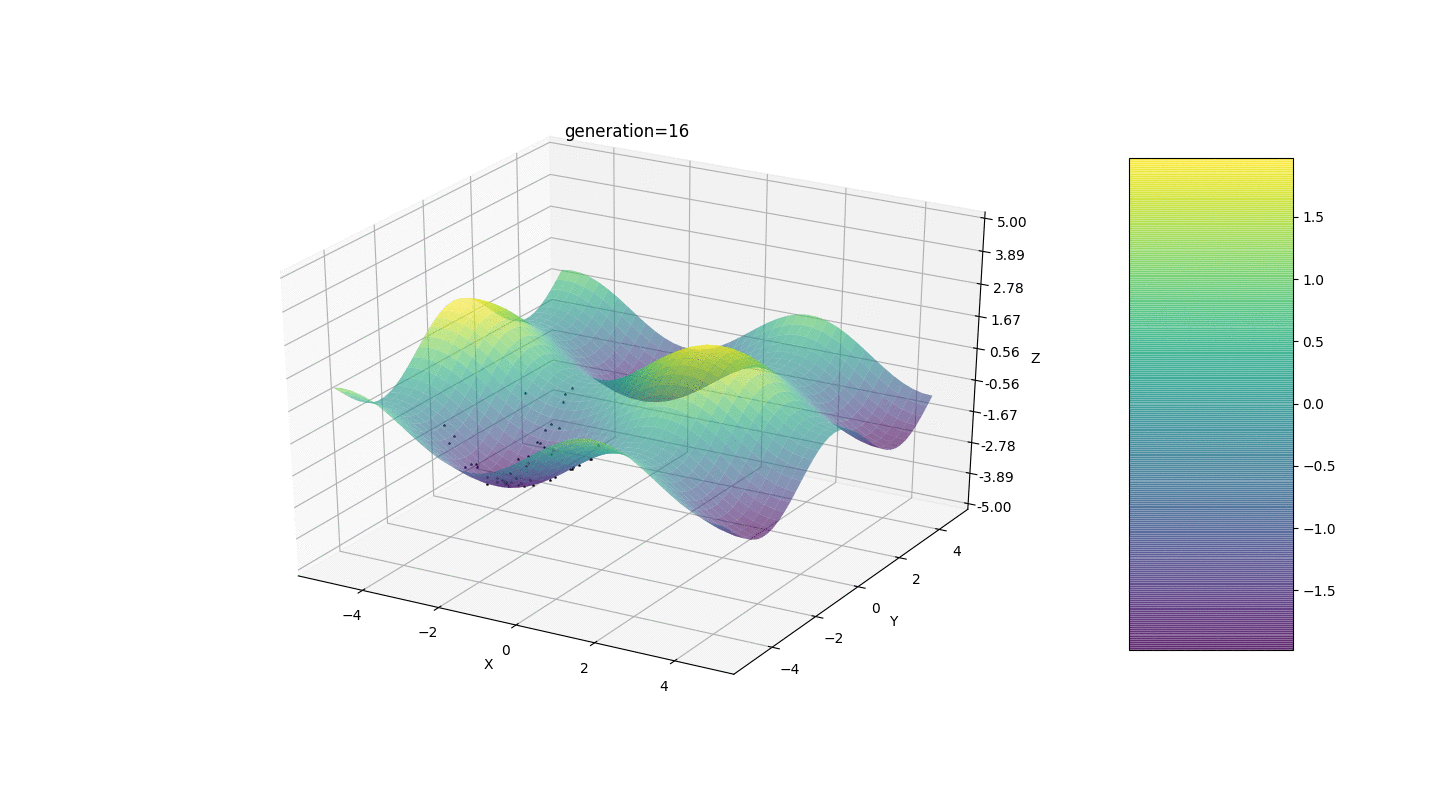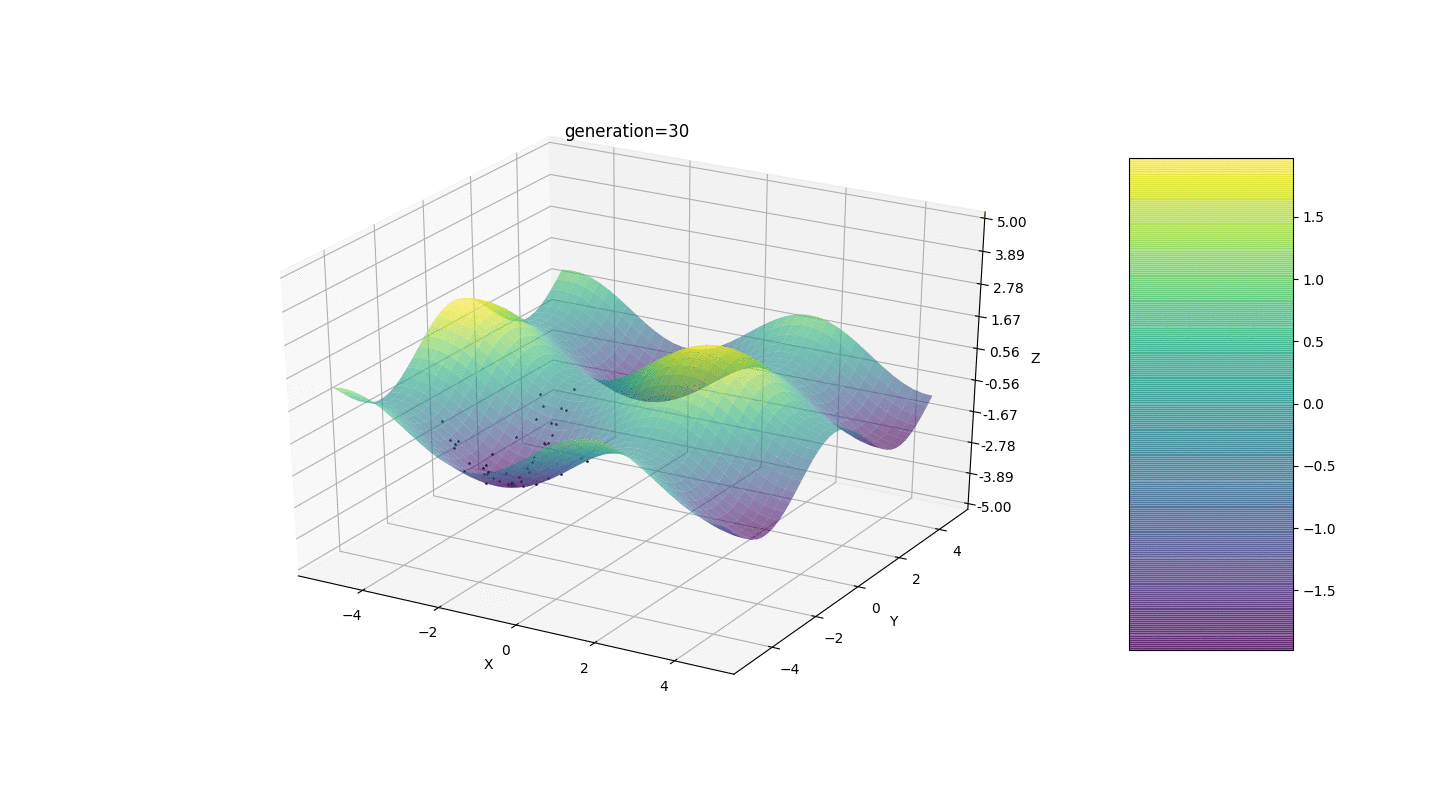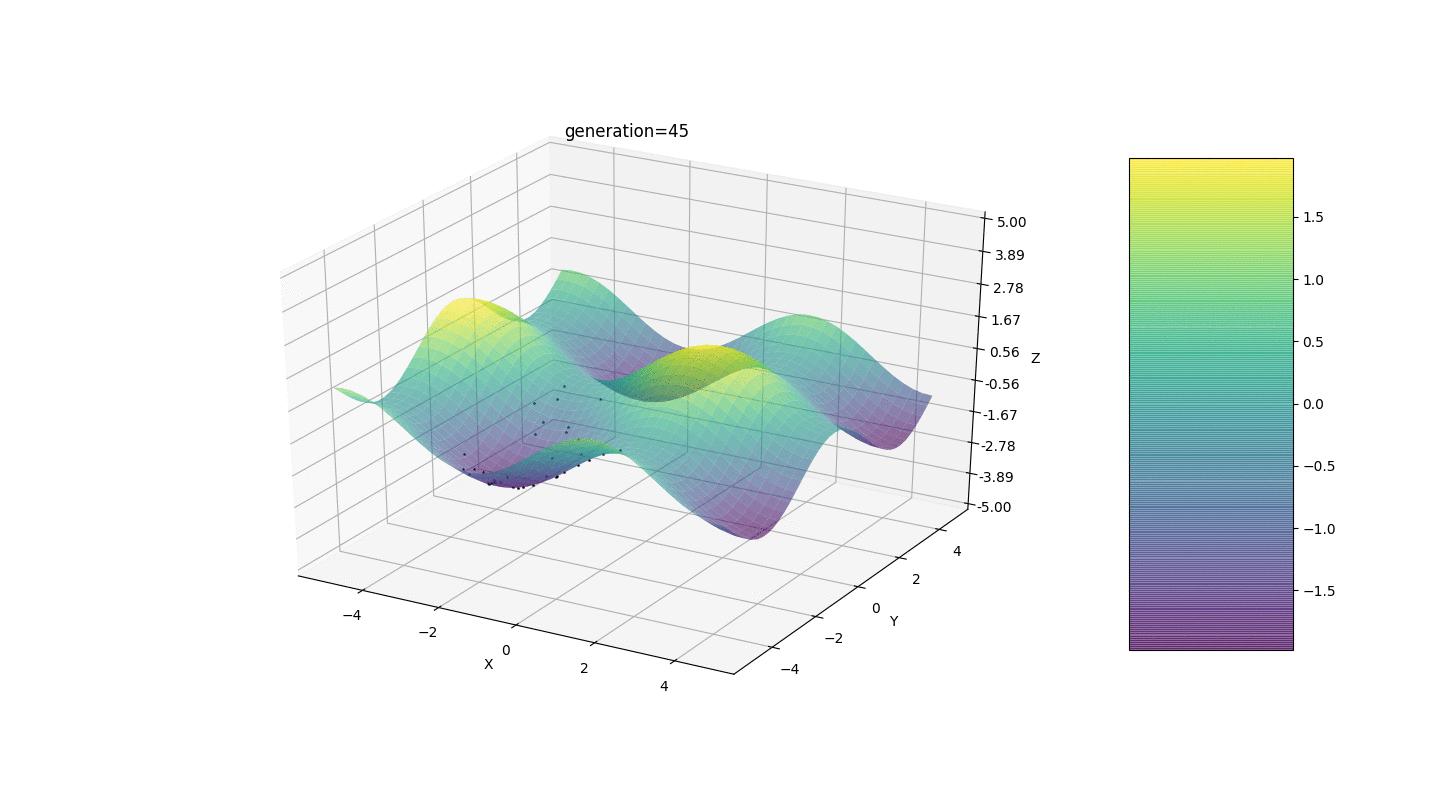
 测试2
测试24X--5ÿ3X2+2ÿ2--2X+1个

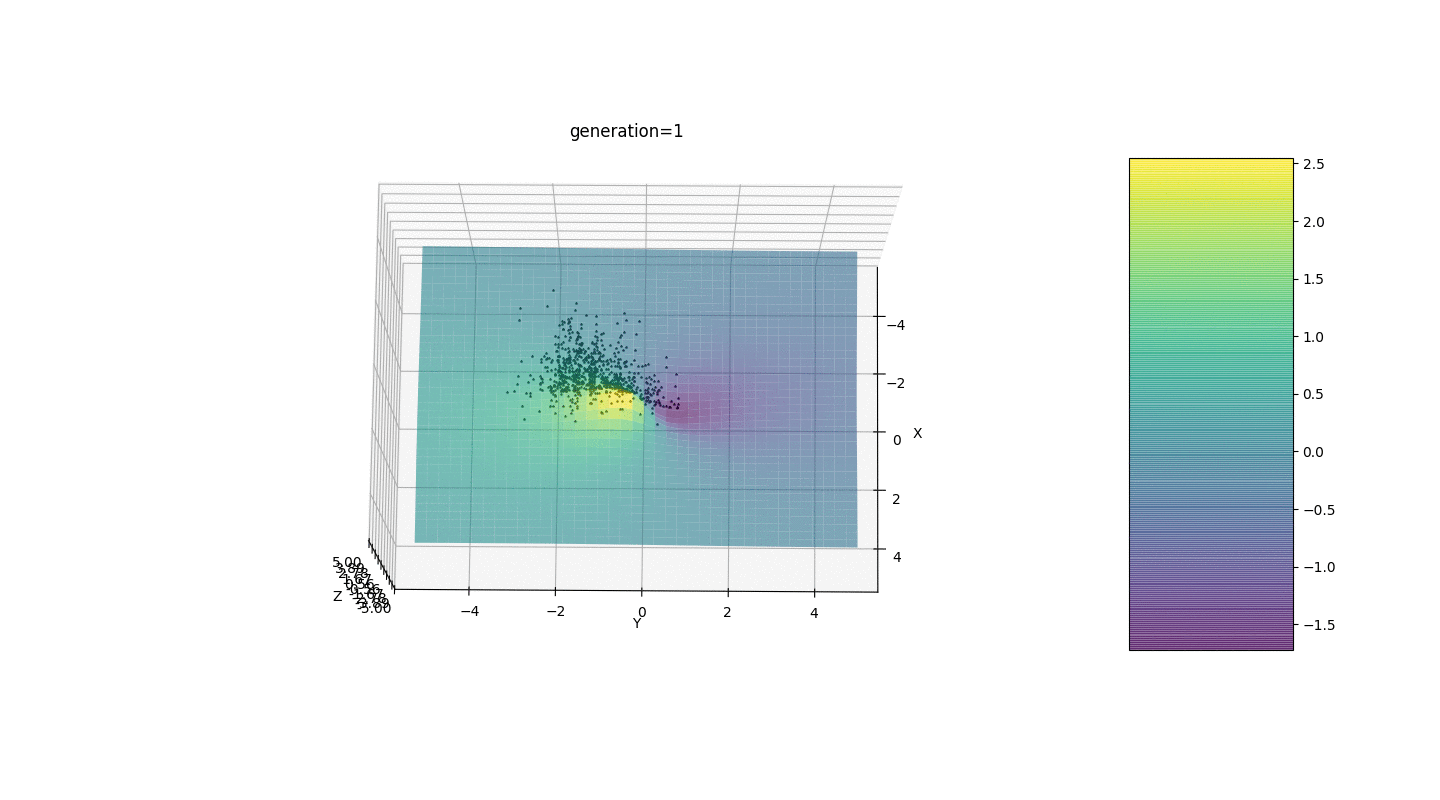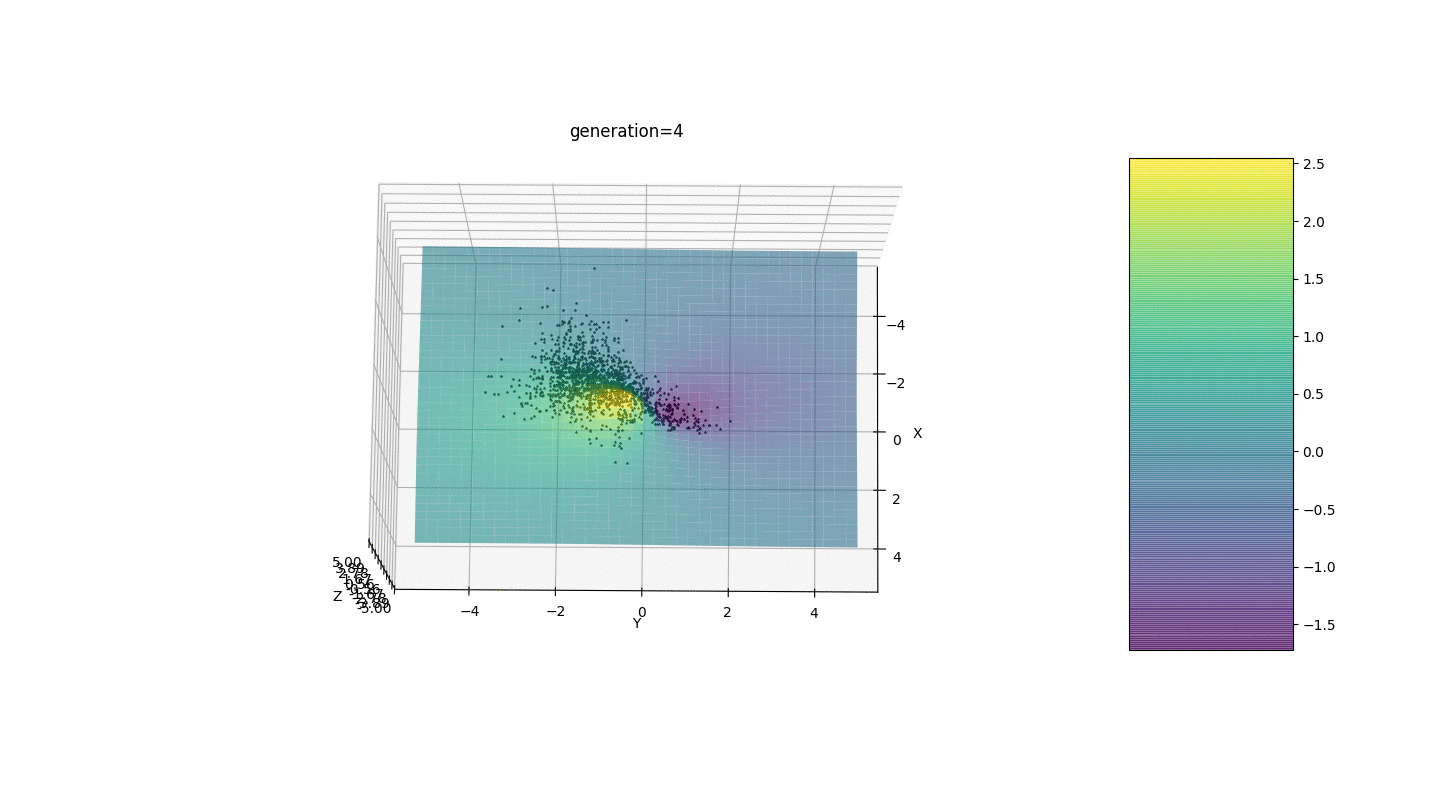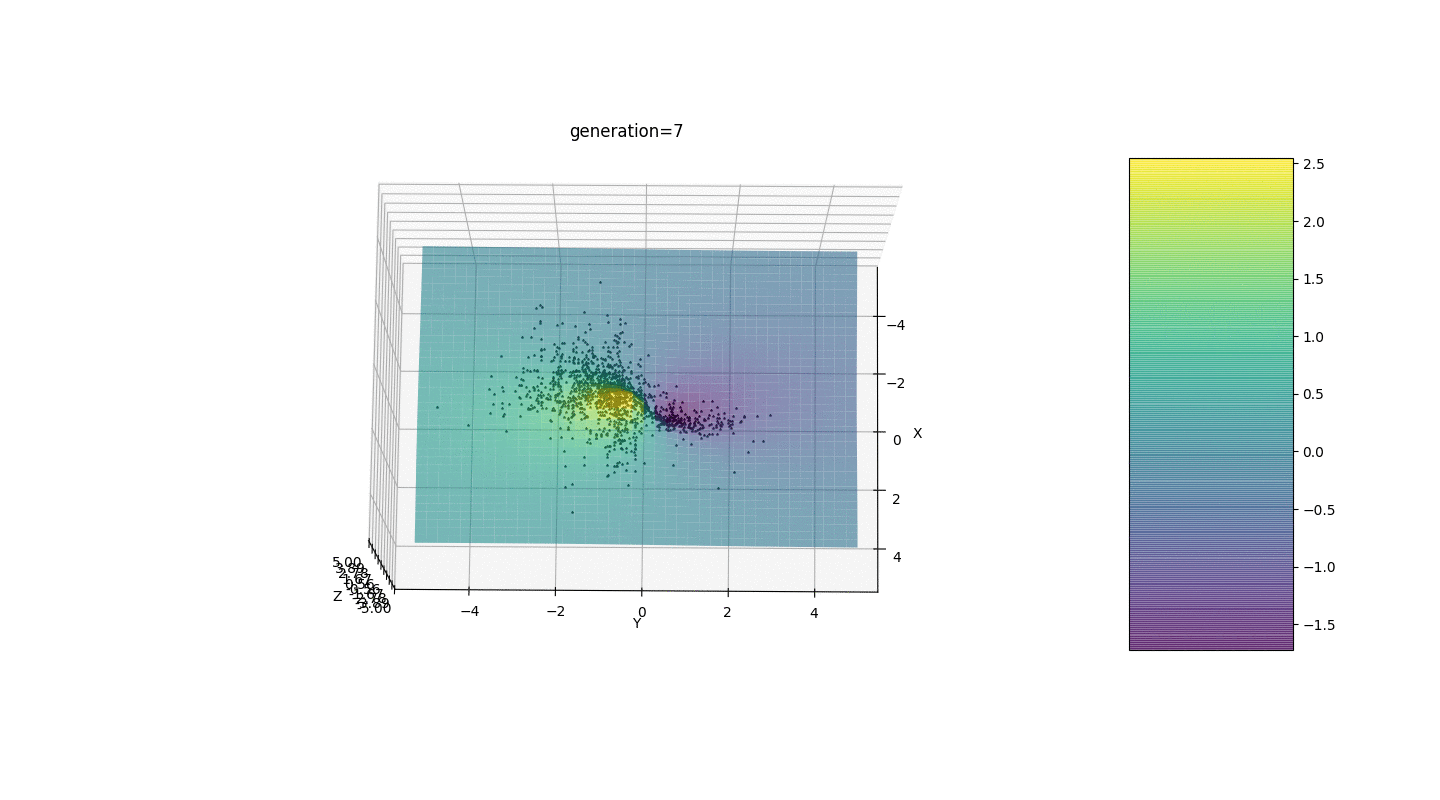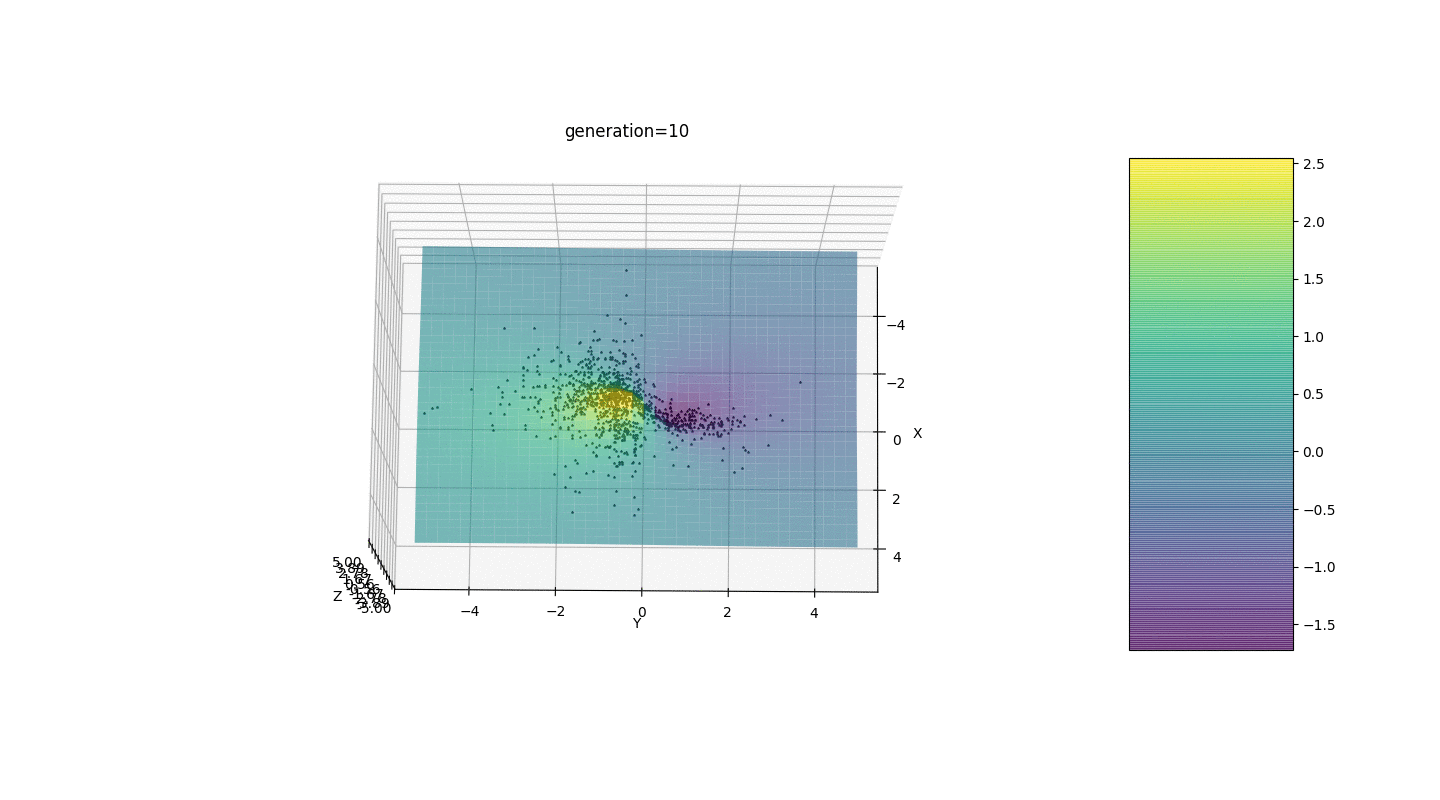
 在通过凝视和随机戳法测试并研究了算法的操作之后,揭示了几种假设模式:
在通过凝视和随机戳法测试并研究了算法的操作之后,揭示了几种假设模式:- , ,
[--1个,1个)
- . , , , ( )- 5-15 , «»
- 零代仅在一个正方形中填充有随机数
[--1个,1个)∗[--1个,1个)
有时这种正方形覆盖了局部极值,这不适合我们
考虑具有以下形式的极值的表面:G(X,ÿ)=∑一世=1个ñFñ(H,X0,ÿ0),F(H,X0,ÿ0)=H∗ËXp(--(X--X0)2--(ÿ--ÿ0)2)
函数g的极值将在点处(X0,ÿ0)
。测试3G(X,ÿ)=F1个(2,0,0)+F2(5,3,3)
G(X,ÿ)=2ËXp(--X2--ÿ2)+5ËXp(--(X--3)2--(ÿ--3)2)
 此示例确认并说明了所有上述观察结果。
此示例确认并说明了所有上述观察结果。遗传算法升级
因此,目前,变异函数非常原始地组成:它从半间隔中添加了随机值[--1个,1个)
突变的基因。这种突变不变性有时会干扰算法的正确操作,但存在纠正此缺陷的有效方法。我们引入一个新参数,我们将其称为“突变范围”,该参数将显示基因突变的间隔时间。让我们使该突变系数与世代数成反比。那些。世代数越高,基因突变越弱。该解决方案使您可以自定义起始区域,并在必要时提高计算的准确性。测试1F(X,ÿ)=s一世ñX

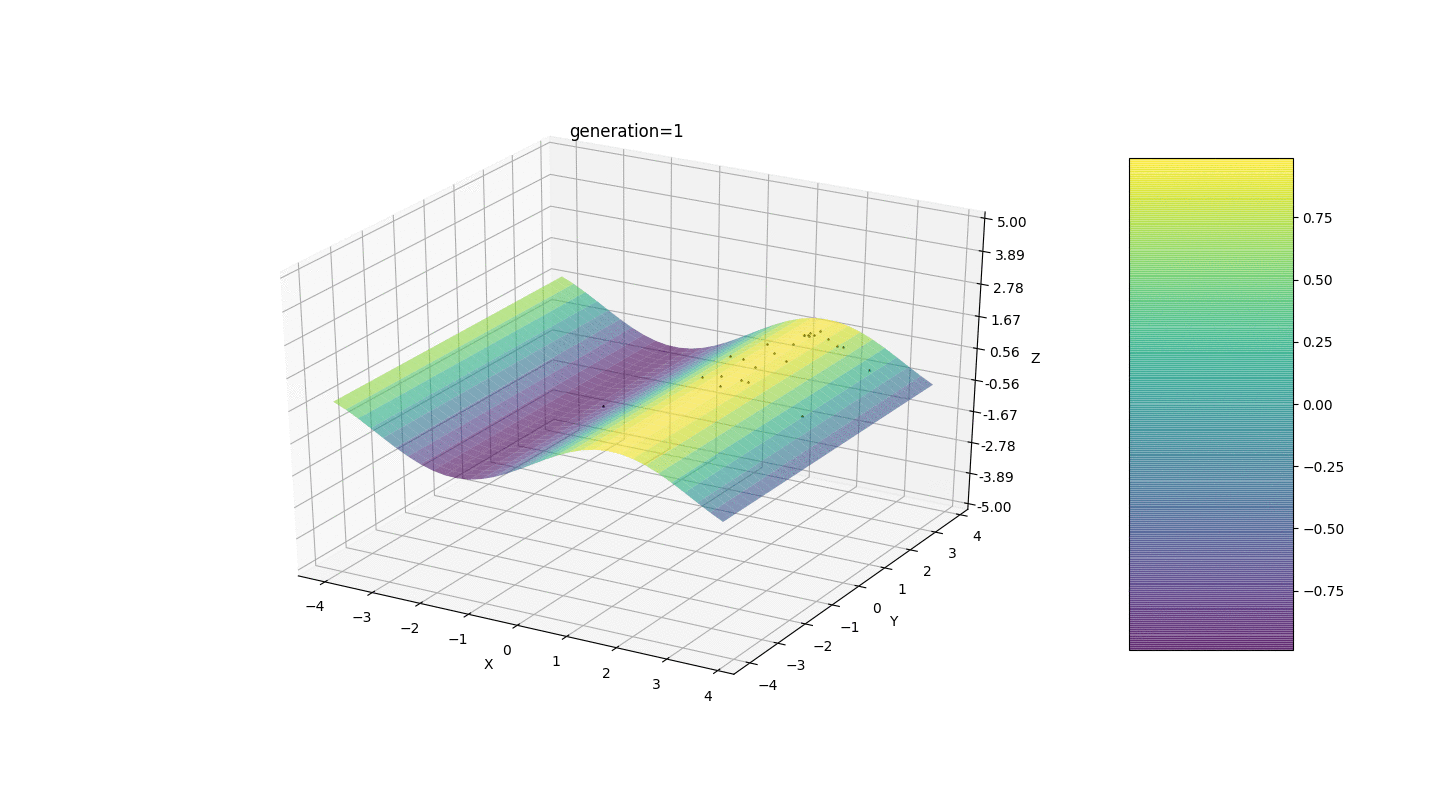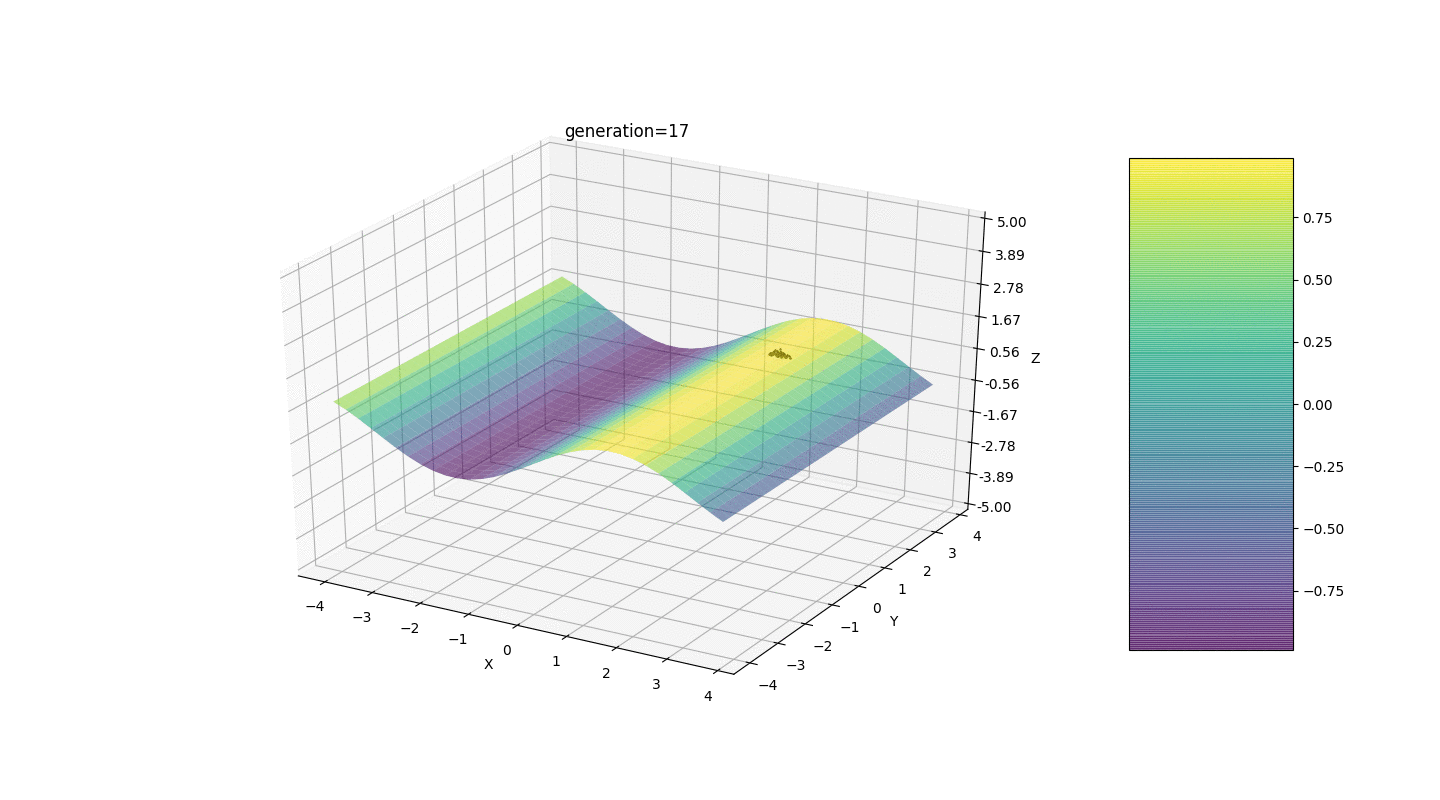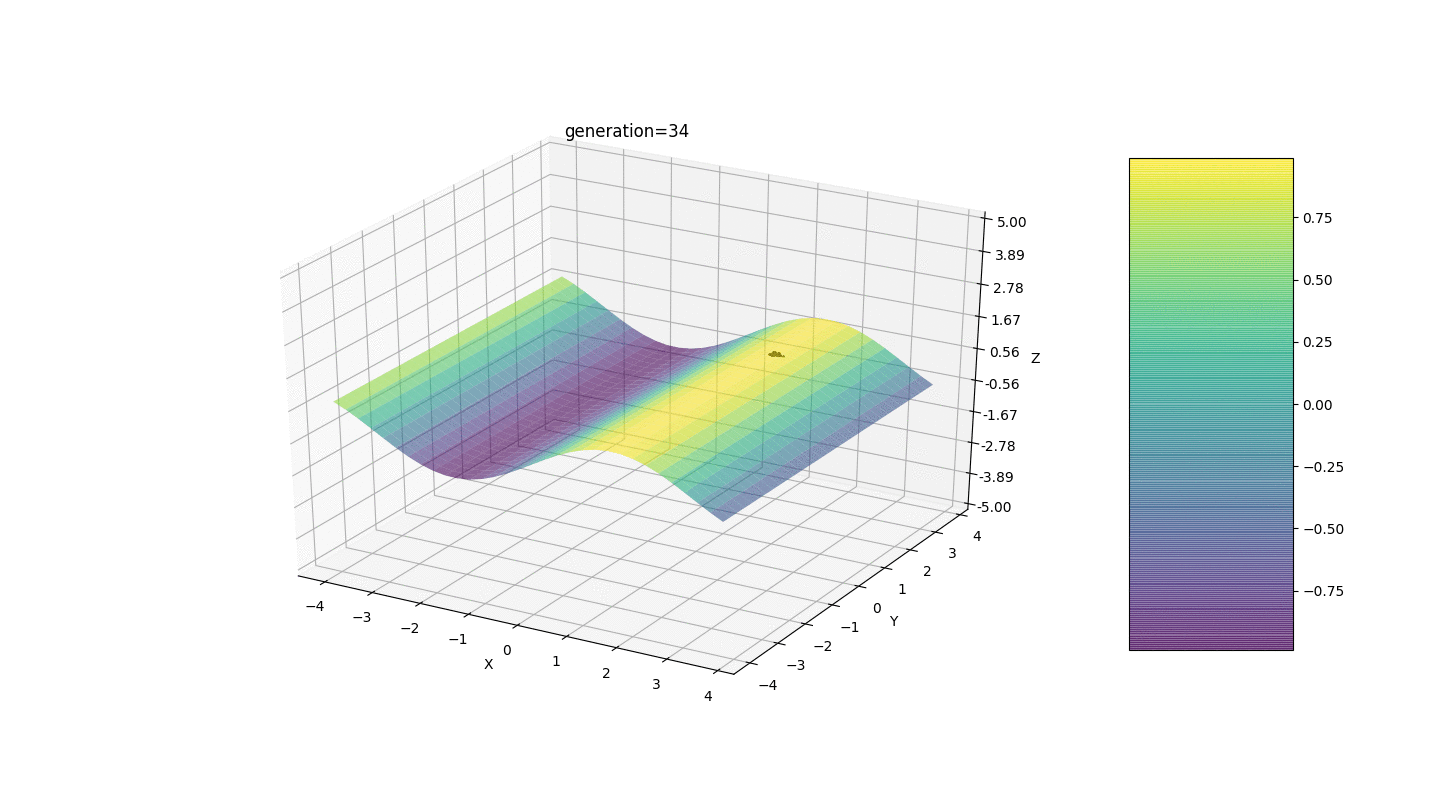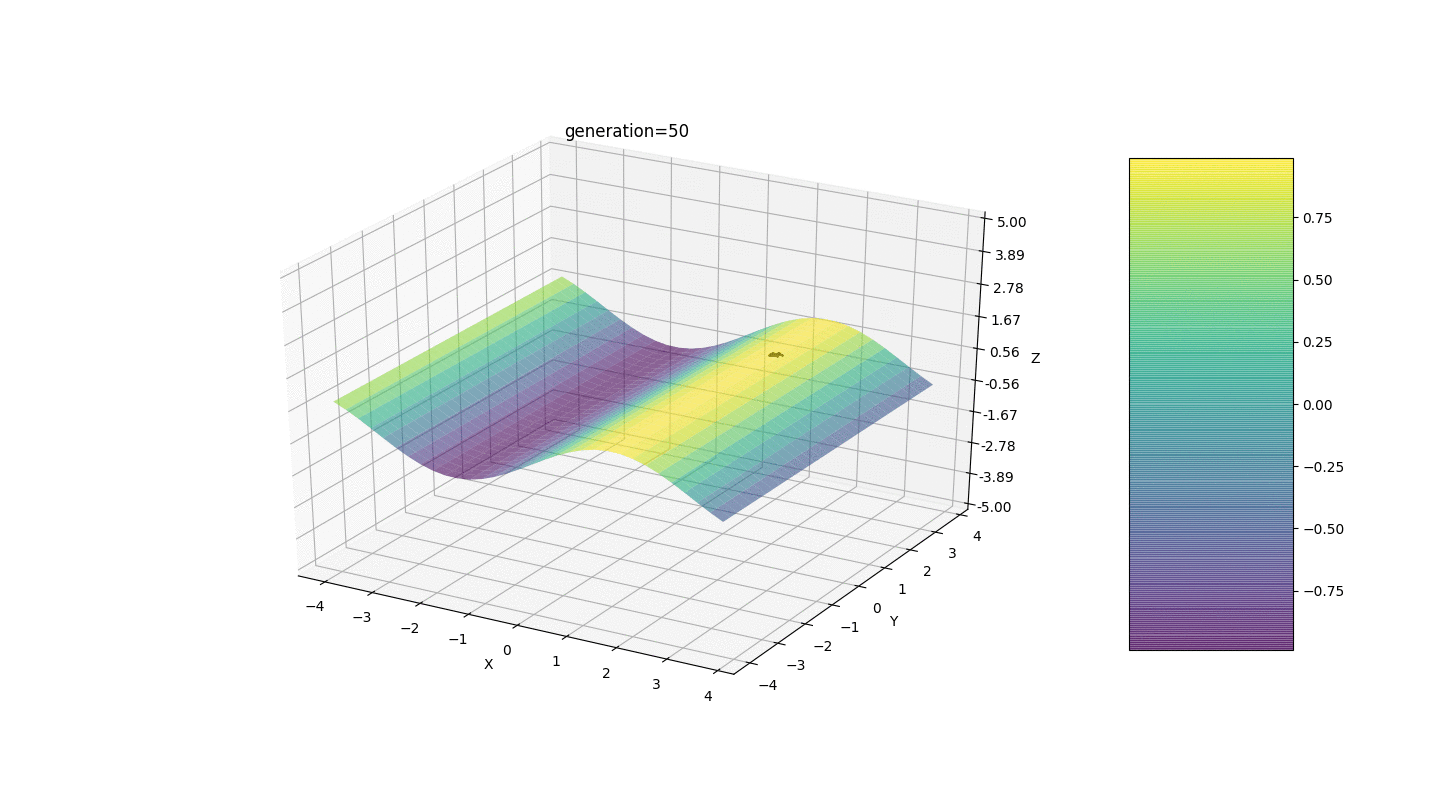
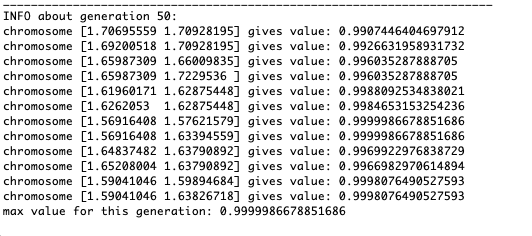 如示例所示,由于波动较小,人口的每一代都越来越收敛到极值并计算出最准确的值。但是局部极端问题呢?考虑一个熟悉的例子。测试2
如示例所示,由于波动较小,人口的每一代都越来越收敛到极值并计算出最准确的值。但是局部极端问题呢?考虑一个熟悉的例子。测试2G(X,ÿ)=F1个(2,0,0)+F2(5,3,3)
G(X,ÿ)=2ËXp(--X2--ÿ2)+5ËXp(--(X--3)2--(ÿ--3)2)


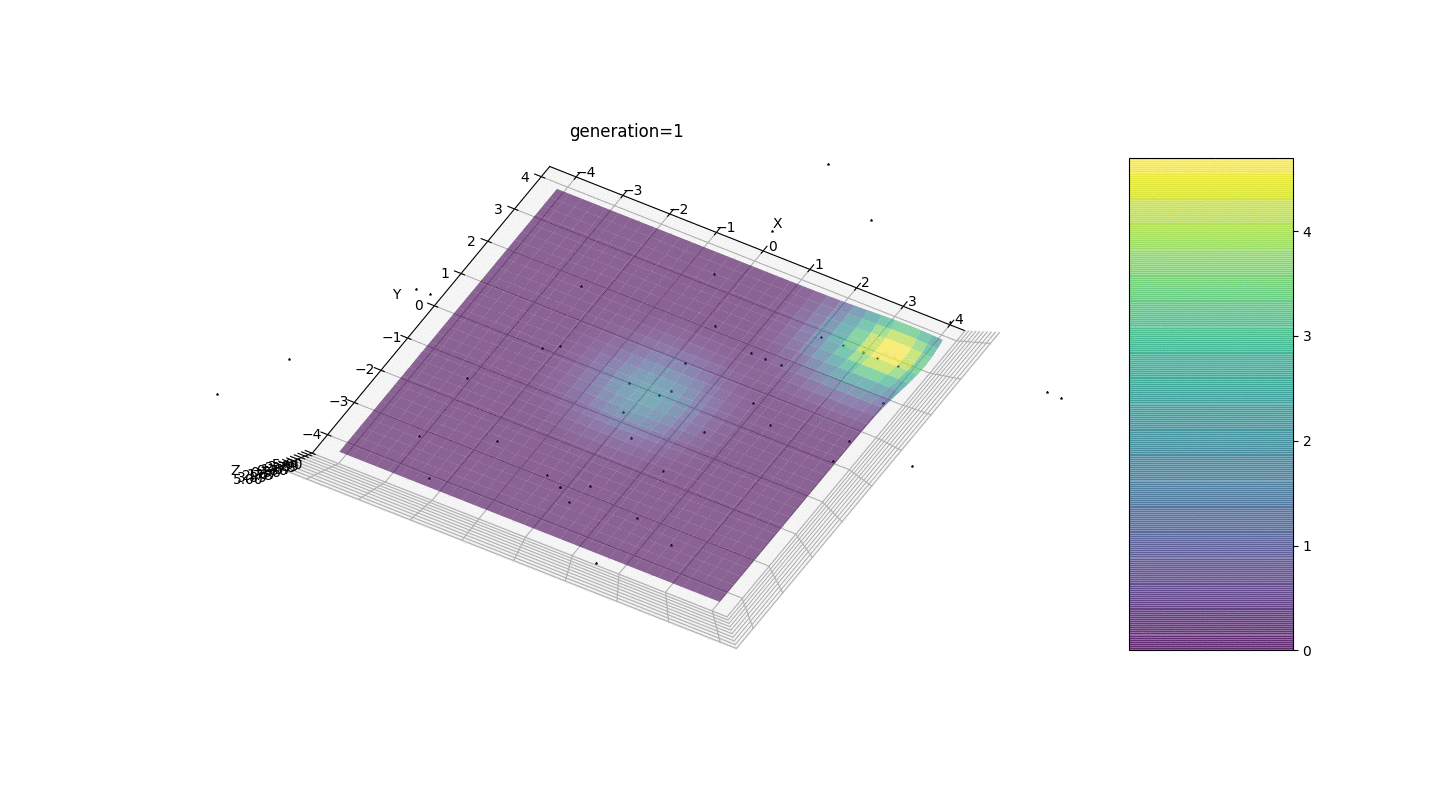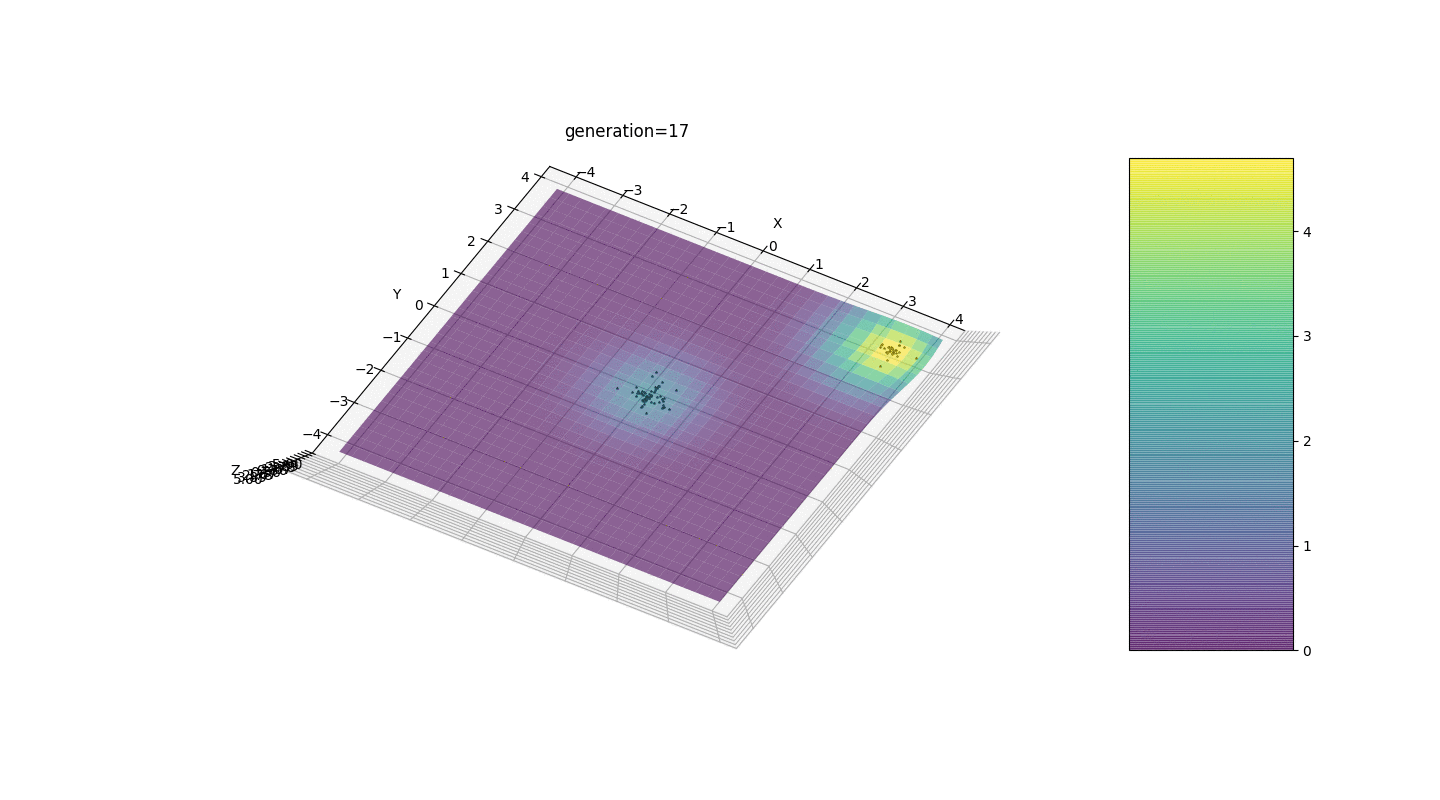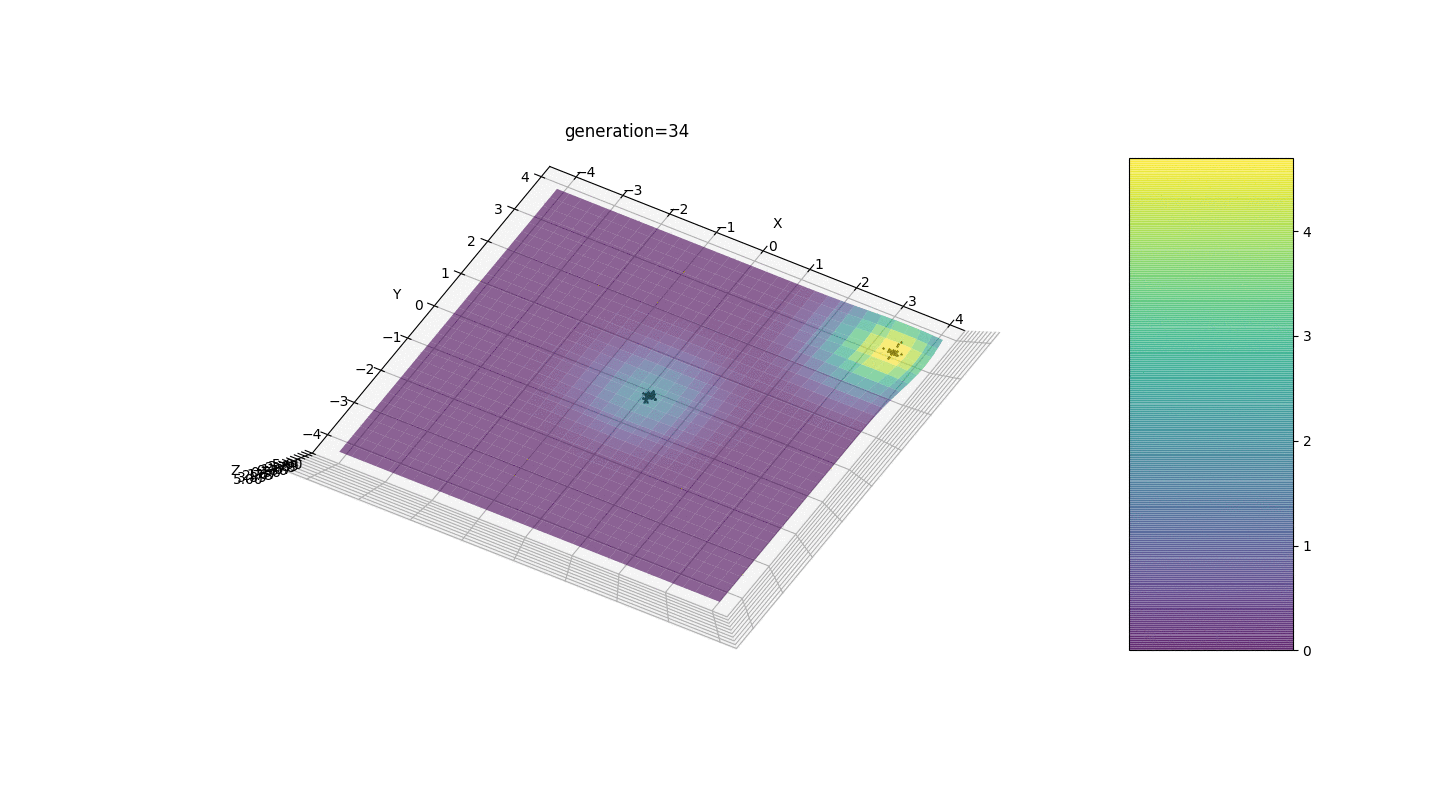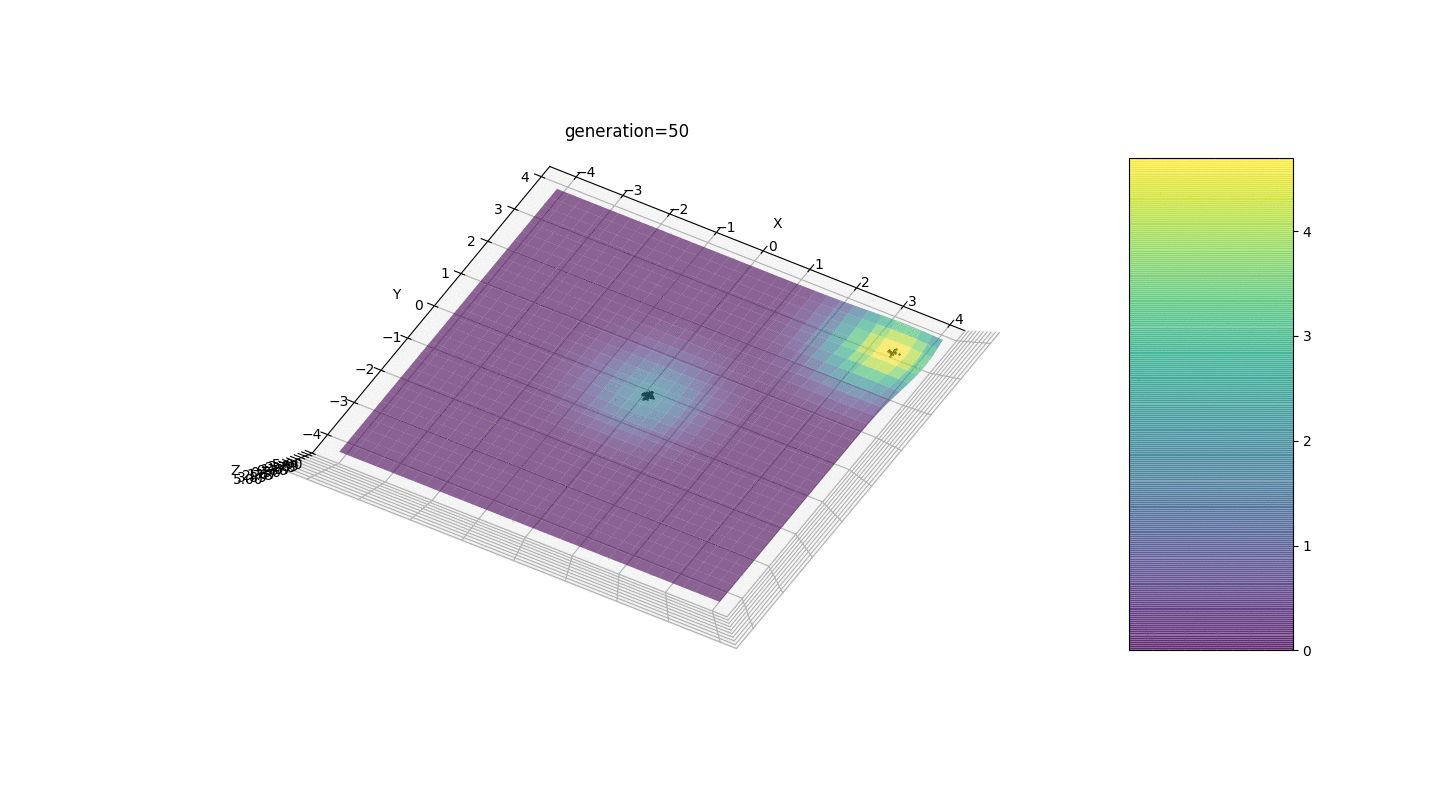
 我们看到现在将人口分成几部分的想法按预期工作了。如果没有这种划分,早期的个体可能会在局部极值处显示出错误的显性基因型,这将导致任务中的错误答案。同样值得注意的是,由于引入了突变对世代数的依赖性,答案的准确性得到了质的提高。
我们看到现在将人口分成几部分的想法按预期工作了。如果没有这种划分,早期的个体可能会在局部极值处显示出错误的显性基因型,这将导致任务中的错误答案。同样值得注意的是,由于引入了突变对世代数的依赖性,答案的准确性得到了质的提高。摘要
我总结一下结果:- 正确的参数集可让您准确地找到两个变量的函数的全局极值
- ,
- ,
...