🤬 👃🏼 👩🏾 前8个JavaScript数据结构 🏗️ 🌤️ 🤰

这听起来是否很熟悉：“我在学习课程后开始进行Web开发”？

也许您想通过数据结构和算法来提高对计算机科学基础知识的了解。今天，我们将使用JS示例讨论一些最常见的数据结构。

1.堆栈（调用）（堆栈）

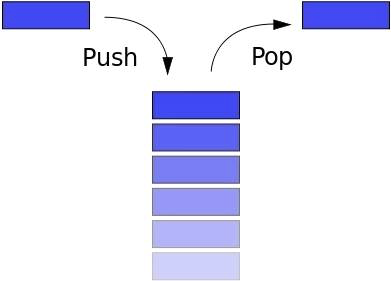堆栈遵循LIFO原则（后进先出-后进先出）。如果您将书本彼此叠放并想拿下最低的书，则先拿上一本，再拿下一本，依此类推。浏览器中的“后退”按钮使您可以（返回）上一页。

堆栈具有以下方法：

推送：添加新项目
弹出：删除顶部元素，将其返回
窥视：返回顶部元素
length：返回堆栈中元素的数量

JS中的数组具有堆栈属性，但是我们将使用功能Stack（）从头开始构建它：

function Stack() {
    this.count = 0
    this.storage = {}

    this.push = function(value) {
        this.storage[this.count] = value
        this.count++
    }

    this.pop = function() {
        if (this.count === 0) return undefined
        this.count--
        let result = this.storage[this.count]
        delete this.storage[this.count]
        return result
    }

    this.peek = function() {
        return this.storage[this.count - 1]
    }

    this.size = function() {
        return this.count
    }
}

2.队列（Queue）

队列类似于堆栈。区别在于队列遵循FIFO原则（先进先出-先进先出）。当您排队时，其中的第一个始终将是第一个。

队列具有以下方法：

排队：进入队列，在末尾添加一个项目
出队：离开队列，删除第一个元素并返回
前：获取第一个元素
isEmpty：检查队列是否为空
size：获取队列中的项目数

JS中的数组具有一些队列属性，因此我们可以将其用于演示：

function Queue() {
    let collection = []

    this.print = function() {
        console.log(collection)
    }

    this.enqueue = function(element) {
        collection.push(element)
    }

    this.dequeue = function() {
        return collection.shift()
    }

    this.front = function() {
        return collection[0]
    }

    this.isEmpty = function() {
        return collection.length === 0
    }

    this.size = function() {
        return collection.length
    }
}

优先顺序（priority）

队列具有高级版本。为每个项目分配优先级，这些项目将进行相应的排序：

function PriorityQueue() {
    ...
    this.enqueue = function(element) {
        if (this.isEmpty()) {
            collection.push(element)
        } else {
            let added = false
            for (let i = 0; i < collection.length; i++) {
                if (element[1] < collection[i][1]) {
                    collection.splice(i, 0, element)
                    added = true
                    break;
                }
            }
            if (!added) {
                collection.push(element)
            }
        }
    }
}

测试：

let pQ = new PriorityQueue()
pQ.enqueue([gannicus, 3])
pQ.enqueue([spartacus, 1])
pQ.enqueue([crixus, 2])
pQ.enqueue([oenomaus, 4])
pQ.print()

结果：

[
    [spartacus, 1],
    [crixus, 2],
    [gannicus, 3],
    [oenomaus, 4]
]

3.链表（节点和链接或指针的链表）（链表）

从字面上看，链表是一个链式数据结构，其中每个节点由两部分组成：节点数据和指向下一个节点的指针。链表和条件数组是带有序列化存储的线性数据结构。区别如下：

标准	数组	清单
内存分配	静态的，在编译时顺序发生	动态，在启动（运行）过程中异步发生
获取物品	索引搜索，高速	搜索所有队列节点，速度不太高
添加/删除项目	由于顺序和静态内存分配，速度较低	由于动态内存分配，速度更高
结构体	一个或多个方向	单向，双向或循环

单链列表具有以下方法：

size：返回节点数
head：返回第一个元素（head-head）
添加：在末尾添加一个元素（尾-尾）
删除：删除多个节点
indexOf：返回节点索引
elementAt：按索引返回节点
addAt：在特定位置插入一个节点（按索引）
removeAt：删除特定节点（按索引）

// 
function Node(element) {
    // 
    this.element = element
    //    
    this.next = null
}

function LinkedList() {
    let length = 0
    let head = null
    this.size = function() {
        return length
    }

    this.head = function() {
        return head
    }

    this.add = function(element) {
        let node = new Node(element)
        if (head === null) {
            head = node
        } else {
            let currentNode = head
            while (currentNode.next) {
                currentNode = currentNode.next
            }
            currentNode.next = node
        }
        length++
    }

    this.remove = function(element) {
        let currentNode = head
        let previousNode
        if (currentNode.element !== element) {
            head = currentNode.next
        } else {
            while (currentNode.element !== element) {
                previousNode = currentNode
                currentNode = currentNode.next
            }
            previousNode.next = currentNode.next
        }
        length--
    }

    this.isEmpty = function() {
        return length === 0
    }

    this.indexOf = function(element) {
        let currentNode = head
        let index = -1
        while (currentNode) {
            index++
            if (currentNode.element === element) {
                return index
            }
            currentNode = currentNode.next
        }
        return -1
    }

    this.elementAt = function(index) {
        let currentNode = head
        let count = 0
        while (count < index) {
            count++
            currentNode = currentNode.next
        }
        return currentNode.element
    }

    this.addAt = function(index, element) {
        let node = new Node(element)
        let currentNode = head
        let previousNode
        let currentIndex = 0
        if (index > length) return false
        if (index === 0) {
            node.next = currentNode
            head = node
        } else {
            while (currentIndex < index) {
                currentIndex++
                previousNode = currentNode
                currentNode = currentNode.next
            }
            node.next = currentNode
            previousNode.next = node
        }
        length++
    }

    this.removeAt = function(index) {
        let currentNode = head
        let previousNode
        let currentIndex = 0
        if (index < 0 || index >= length) return null
        if (index === 0) {
            head = currentIndex.next
        } else {
            while (currentIndex < index) {
                currentIndex++
                previousNode = currentNode
                currentNode = currentNode.next
            }
            previousNode.next = currentNode.next
        }
        length--
        return currentNode.element
    }
}

4.收集（值）（设置）

集合（许多）是数学的基本概念之一：一组定义明确且孤立的对象。ES6引入了一个与数组有些相似的集合。但是，该集合不允许包含重复的元素，并且不包含索引。

标准集合具有以下方法：

值：返回集合中的所有项目
size：返回元素数
具有：检查项目是否在集合中
添加：添加项目
删除：删除一个项目
并集：返回两个集合的交集区域
差异：返回两个集合之间的差异
子集：检查一个集合是否是另一个集合的子集

//   Set  JS
function MySet() {
    let collection = []
    this.has = function(element) {
        return (collection.indexOf(element) !== -1)
    }

    this.values = function() {
        return collection
    }

    this.size = function() {
        return collection.length
    }

    this.add = function(element) {
        if (!this.has(element)) {
            collection.push(element)
            return true
        }
        return false
    }

    this.remove = function(element) {
        if (this.has(element)) {
            index = collection.indexOf(element)
            collection.splice(index, 1)
            return true
        }
        return false
    }

    this.union = function(otherSet) {
        let unionSet = new MySet()
        let firstSet = this.values()
        let secondSet = otherSet.values()
        firstSet.forEach(i => unionSet.add(i))
        secondSet.forEach(i => unionSet.add(i))
    }

    this.intersection = function(otherSet) {
        let intersectionSet = new MySet()
        let firstSet = this.values()
        firstSet.forEach(function(e) {
            if (otherSet.has(e)) {
                intersectionSet.add(e)
            }
        })
        return intersectionSet
    }

    this.difference = function(otherSet) {
        let differenceSet = new MySet()
        let firstSet = this.values()
        firstSet.forEach(function(e) {
            if (!otherSet.has(e)) {
                differenceSet.add(e)
            }
        })
        return differenceSet
    }

    this.subset = function(otherSet) {
        lat firstSet = this.values()
        return firstSet.every(value => otherSet.has(value))
    }
}

5.哈希表（Hash Table）

哈希表是一种基于键值构建的数据结构。由于通过键搜索值的速度很高，因此它用于诸如Map，Dictionary和Object的结构中。如图所示，哈希表具有哈希函数，该哈希函数将键转换为用作键的名称（值）的数字列表。键值搜索时间可以达到O（1）。相同的键必须返回相同的值-这是哈希函数的本质。

哈希表具有以下方法：

添加：添加键/值对
删除：删除一对
查找：按键查找值

function hash(string, max) {
    let hash = 0
    for (let i = 0; i < string.length; i++) {
        hash += string.charCodeAt(i)
    }
    return hash % max
}

function HashTable() {
    let storage = []
    const storageLimit = 4

    this.add = function(key, value) {
        let index = hash(key, storageLimit)
        if (storage[index] === undefined) {
            storage[index] = [
                [key, value]
            ]
        } else {
            let inserted = false
            for (let i = 0; i < storage[index].len; i++) {
                if (storage[index][i][0] === key) {
                    storage[index][i][1] = value
                    inserted = true
                }
            }
            if (inserted === false) {
                storage[index].push([key, value])
            }
        }
    }

    this.remove = function(key) {
        let index = hash(key, storageLimit)
        if (storage[index].length === 1 && storage[index][0][0] === key) {
            delete storage[index]
        } else {
            for (let i = 0; i < storage[index]; i++) {
                if (storage[index][i][0] === key) {
                    delete storage[index][i]
                }
            }
        }
    }

    this.lookup = function(key) {
        let index = hash(key, storageLimit)
        if (storage[index] === undefined) {
            return undefined
        } else {
            for (let i = 0; i < storage[index].length; i++) {
                if (storage[index][i][0] === key) {
                    return storage[index][i][1]
                }
            }
        }
    }
}

6.树

树结构是多层（多级）结构。它也是一种非线性结构，与数组，堆栈和队列不同。就添加和搜索元素而言，此结构非常有效。这是树结构的一些概念：

root：根元素，没有父元素
父节点：顶层（级别）的直接节点，只能有一个
子节点：较低级别的直接节点，可能有几个
兄弟姐妹：一个父节点的子节点
叶：没有“孩子”的结
边缘：节点之间的分支或链接（链接）
路径：从起始节点到目标元素的路径（链接集）
树的高度：从特定元素到没有子节点的最长路径的链接数
节点深度：从根节点到特定元素的链接数。
节点度：后代数

这是二叉搜索树（BST）的示例。每个节点只有两个后代，左（子）节点小于当前（父）节点，右（子）节点较大：该

树的方法如下：

添加：添加节点
findMin：获取最小节点
findMax：获取最大节点
查找：查找特定节点
isPresent：检查特定节点
删除：删除节点

class Node {
    constructor(data, left = null, right = null) {
        this.data = data
        this.left = left
        this.right = right
    }
}

class BST {
    constructor() {
        this.root = null
    }

    add(data) {
        const node = this.root
        if (node === null) {
            this.root = new Node(data)
            return
        } else {
            const searchTree = function(node) {
                if (data < node.data) {
                    if (node.left === null) {
                        node.left = new Node(data)
                        return
                    } else if (node.left !== null) {
                        return searchTree(node.left)
                    }
                } else if (data > node.data) {
                    if (node.right === null) {
                        node.right = new Node(data)
                        return
                    } else if (node.right !== null) {
                        return searchTree(node.right)
                    }
                } else {
                    return null
                }
            }
            return searchTree(node)
        }
    }

    findMin() {
        let current = this.root
        while (current.left !== null) {
            current = current.left
        }
        return current.data
    }

    findMax() {
        let current = this.root
        while (current.right !== null) {
            current = current.right
        }
        return current.data
    }

    find(data) {
        let current = this.root
        while (current.data !== data) {
            if (data < current.data) {
                current = current.left
            } else {
                current = current.right
            }
            if (current === null) {
                return null
            }
        }
        return current
    }

    isPresent(data) {
        let current = this.root
        while (current) {
            if (data === current.data) {
                return true
            }
            data < current.data ? current = current.left : current = current.right
        }
        return false
    }

    remove(data) {
        const removeNode = function(node, data) {
            if (node === null) return null
            if (data === node.data) {
                //  
                if (node.left === null && node.right === null) return null
                //   
                if (node.left === null) return node.right
                //   
                if (node.right === null) return node.left
                //   
                let tempNode = node.right
                while (tempNode.left !== null) {
                    tempNode = tempNode.left
                }
                node.data = tempNode.data
                node.right = removeNode(node.right, tempNode.data)
                return node
            } else if (data < node.data) {
                node.left = removeNode(node.right, data)
                return node
            } else {
                node.right = removeNode(node.right, data)
                return node
            }
        }
        this.root = removeNode(this.root, data)
    }
}

测试：

const bst = new BST()
bst.add(4)
bst.add(2)
bst.add(6)
bst.add(1)
bst.add(3)
bst.add(5)
bst.add(7)
bst.remove(4)
console.log(bst.findMin())
console.log(bst.findMax())
bst.remove(7)
console.log(bst.findMax())
console.log(bst.isPresent(4))

结果：

1
7
6
false

7.加载的（前缀）树（Trie，读为“ try”）

前缀树是搜索树的一种。其中的数据按顺序存储（逐步）-每个树节点代表一个步骤。字典中使用了前缀树，因为它大大加快了搜索速度。

每个树节点都是字母的一个字母，跟随一个分支会导致一个单词的形成。它还包含一个“布尔指示器”，用于确定当前节点是最后一个字母。

前缀树具有以下方法：

添加：在字典中添加一个单词
isWord：检查一个单词
打印：返回所有单词

//  
function Node() {
    this.keys = new Map()
    this.end = false
    this.setEnd = function() {
        this.end = true
    }
    this.isEnd = function() {
        return this.end
    }
}

function Trie() {
    this.root = new Node()
    this.add = function(input, node = this.root) {
        if (input.length === 0) {
            node.setEnd()
            return
        } else if (!node.keys.has(input[0])) {
            node.keys.set(input[0], new Node())
            return this.add(input.substr(1), node.key.get(input[0]))
        } else {
            return this.add(input.substr(1), node.keys.get(input[0]))
        }
    }

    this.isWord = function(word) {
        let node = this.root
        while (word.length > 1) {
            if (node.keys.has(word[0])) {
                return false
            } else {
                node = node.keys.get(word[0])
                word = word.substr(1)
            }
        }
        return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false
    }

    this.print = function() {
        let words = new Array()
        let search = function(node = this.root, string) {
            if (node.keys.size !== 0) {
                for (let letter of node.keys.keys()) {
                    search(node.keys.get(letter), string.concat(letter))
                }
                if (node.isEnd()) {
                    words.push(string)
                }
            } else {
                string.length > 0 ? words.push(string) : undefined
                return
            }
        }
        search(this.root, new String())
        return words.length > 0 ? words : null
    }
}

8.图（graph）（图）

图（也称为网络）是互连节点的集合。根据链接是否有方向，有两种图形-定向图和非定向图。图形可在任何地方使用，例如，以计算导航应用程序中的最佳路线或在社交网络上创建推荐列表。

图形可以列表或矩阵的形式呈现。

清单

在这种情况下，所有父节点都位于左侧，而其子节点位于右侧。

矩阵

在这种情况下，节点按行和列分布，行和列的交点表示节点之间的关系：0表示未连接节点，1表示已连接节点。

通过两种方法搜索图形-广度优先搜索（Breath-First-Search，BFS）和深度深度搜索（Depth-First-Search，DFS）。

考虑BFS：

function bfs(graph, root) {
    let nodesLen = {}
    for (let i = 0; i < graph.length; i++) {
        nodesLen[i] = Infinity
    }
    nodesLen[root] = 0
    let queue = [root]
    let current
    while (queue.length !== 0) {
        current = queue.shift()

        let curConnected = graph[current]
        let neighborIdx = []
        let idx = curConnected.indexOf(1)
        while (idx !== -1) {
            neighborIdx.push(idx)
            idx = curConnected.indexOf(1, idx + 1)
        }
        for (let i = 0; i < neighborIdx.length; i++) {
            if (nodesLen[neighborIdx[i]] === Infinity) {
                nodesLen[neighborIdx[i]] = nodesLen[current] + 1
                queue.push(neighborIdx[i])
            }
        }
    }
    return nodesLen
}

测试：

let graph = [
    [0, 1, 1, 1, 0],
    [0, 0, 1, 0, 0],
    [1, 1, 0, 0, 0],
    [0, 0, 0, 1, 0],
    [0, 1, 0, 0, 0]
]
console.log(bfs(graph, 1))

结果：

{
    0: 2,
    1: 0,
    2: 1,
    3: 3,
    4: Infinity
}

这就是我的全部。希望您找到对自己有用的东西。编码愉快！

前8个JavaScript数据结构