Get best of the week

Python的一般财务分析（第3部分）

所有提出的计算后，这和本刊物，我们可以深入研究的统计分析，并考虑最小二乘法。statsmodels库用于此目的，它允许用户检查数据，评估统计模型并执行统计测试。本文和本文均以此为依据。以下链接提供了英语使用功能的说明。

首先，有一点理论：

关于线性回归


当假设因变量（我们正在尝试预测的变量）和自变量（用于预测的变量和/或变量）之间存在线性关系时，将线性回归用作预测模型。

在最简单的情况下，考虑时，将使用一个变量来尝试预测另一个变量。在这种情况下的公式如下：

Y = C + M * X

  • Y =因变量（结果/预测/估计）
  • C =常数（Y截距）
  • M =回归线的斜率（估计线的斜率或斜率；如果X增加一个单位，则Y平均增加的量）
  • X =自变量（预测Y中使用的预测变量）

实际上，因变量和几个自变量之间也可能存在关系。对于这些类型的模型（假设线性），我们可以使用以下形式的多元线性回归：

Y = C + M1X1 + M2X2 + ...

Beta比率


例如，在此页面上已经有很多关于此系数的文章，

简要地讲，如果您不进行详细介绍，则可以按以下方式对其进行表征：

具有beta系数的股票：

  • 零表示股票与指数之间没有相关性
  • 单位表示股票与指数具有相同的波动性
  • 大于一个-表示该股票的获利能力（以及因此的风险）高于该指数
  • 少于一只-波动性股票少于指数

换句话说，如果股票增加14％，而市场仅增加10％，那么股票的beta系数将为1.4。通常，具有较高beta的市场可以提供更好的回报条件（并因此带来风险）。

图片

实践


以下Python代码包含一个线性回归示例，其中输入变量是Moscow Exchange Index的收益率，估计变量是Aeroflot股票的收益率。

为了避免记住如何下载数据并将数据带到计算所必需的形式，从下载数据的那一刻起一直给出代码，直到获得结果为止。这是使用statsmodels在Python中进行线性回归的完整语法：

# 
import pandas as pd
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

# 
ticker = ['AFLT.ME','IMOEX.ME']
stock = yf.download(ticker)

#    
all_adj_close = stock[['Adj Close']]

#   
all_returns = np.log(all_adj_close / all_adj_close.shift(1))

#      
aflt_returns = all_returns['Adj Close'][['AFLT.ME']].fillna(0)

#      
moex_returns = all_returns['Adj Close'][['IMOEX.ME']].fillna(0)


#   DataFrame

return_data = pd.concat([aflt_returns, moex_returns], axis=1)[1:]
return_data.columns = ['AFLT.ME', 'IMOEX.ME']


#      X  y
X = sm.add_constant(return_data['IMOEX.ME'])
y = return_data['AFLT.ME']


#  
model_moex = sm.OLS(y,X).fit()

#  
print(model_moex.summary())

图片

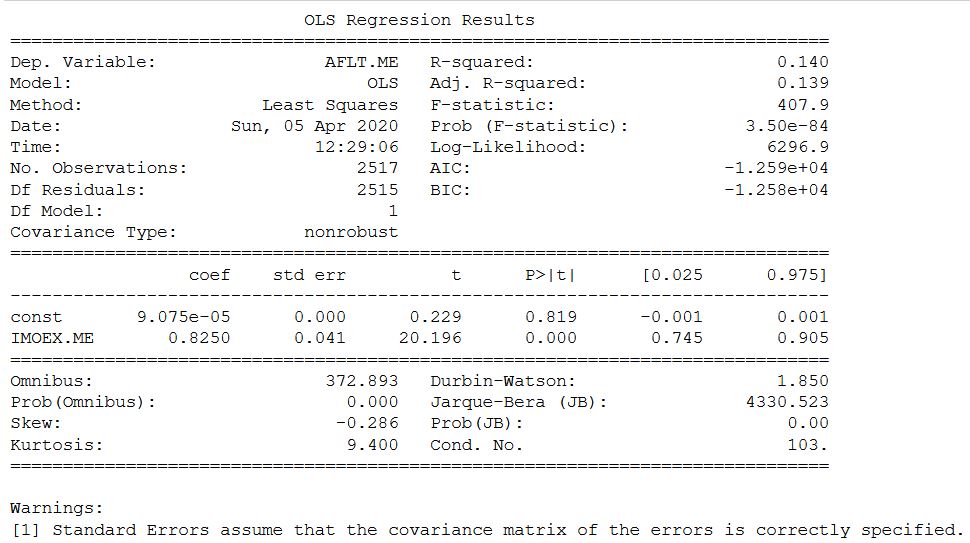在yahoo网站上，Mosbirzhi的beta系数略有不同。但老实说，我必须承认，来自俄罗斯证券交易所的其他一些股票的计算结果显示出更大的差异，但在此区间内。

图片

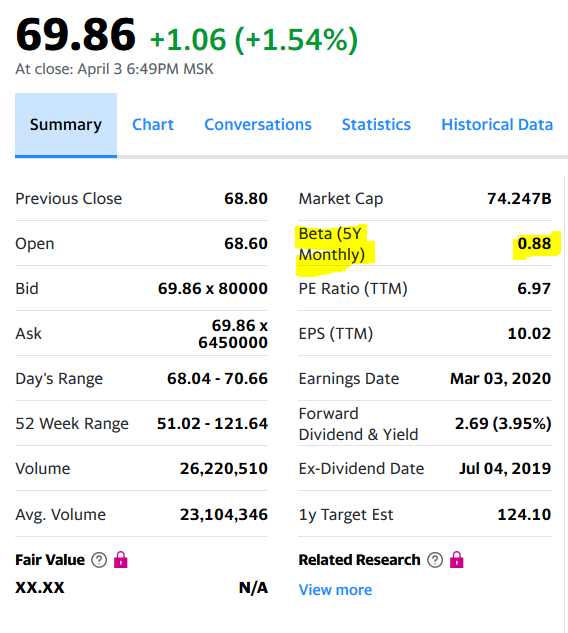FB股票和SP500指数的分析相同。在这里，与原始计算一样，是通过月收益率进行的。

sp_500 = yf.download('^GSPC')
fb = yf.download('FB')

#    
fb = fb.resample('BM').apply(lambda x: x[-1])
sp_500 = sp_500.resample('BM').apply(lambda x: x[-1])

monthly_prices = pd.concat([fb['Close'], sp_500['Close']], axis=1)
monthly_prices.columns = ['FB', '^GSPC']

monthly_returns = monthly_prices.pct_change(1)
clean_monthly_returns = monthly_returns.dropna(axis=0)  

X = clean_monthly_returns['^GSPC']
y = clean_monthly_returns['FB']

X1 = sm.add_constant(X)

model_fb_sp_500 = sm.OLS(y, X1)

results_fb_sp_500 = model_fb_sp_500.fit()
print(results_fb_sp_500.summary())

图片

图片

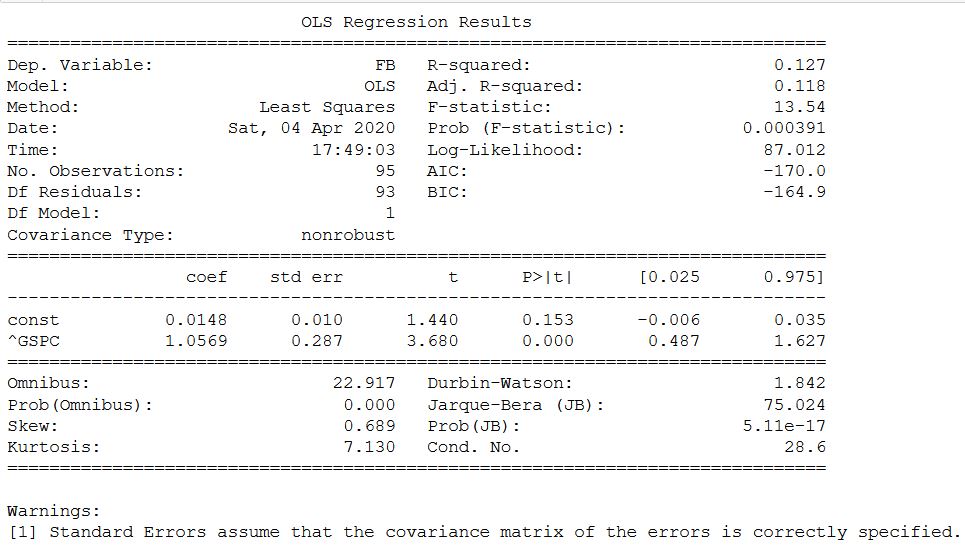
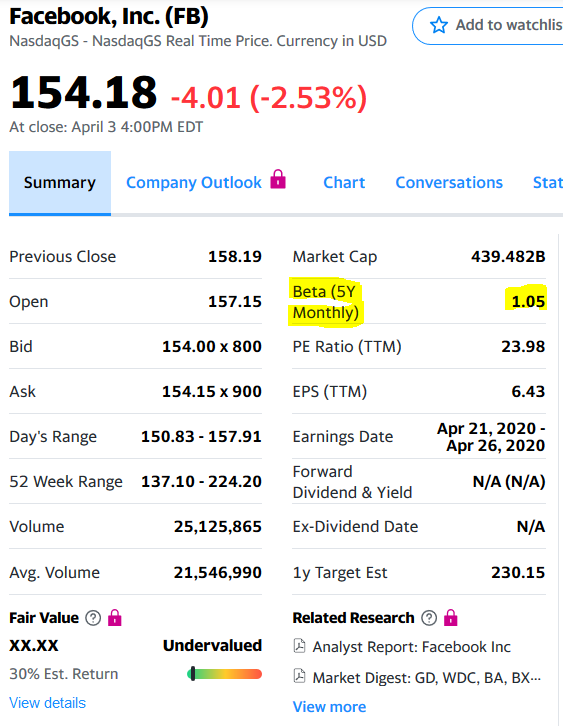在这种情况下，一切都重合了，并确认了使用statsmodels确定beta系数的可能性。

好吧，作为一项奖励-如果您只想获取beta-您想将系数和其他统计信息放在一边，那么建议使用另一代码来计算它：

from scipy import stats
slope, intercept, r_value, p_value, std_err = stats.linregress(X, y)

print(slope)

1.0568997978702754

没错，这并不意味着应该忽略所有其他获得的值，但是需要掌握统计信息才能理解它们。我将从获得的值中摘录一小段：

  • R平方，它是确定系数，取值从0到1.系数的值越接近1，则相关性越强;
  • 调整 R平方-根据观察次数和自由度数调整R平方;
  • std err-系数估计的标准误差；
  • P> | t | -p值小于0.05的值被认为具有统计学意义；
  • 0.025和0.975是置信区间的下限值和上限值。
  • 等等

目前为止就这样了。当然，寻找不同价值之间的关系以通过一个预测另一个并获得利润是很有意义的。在国外来源之一中，该指数是通过利率和失业率来预测的。但是，如果可以从中央银行的网站获取俄罗斯利率的变化，那么我会继续寻找其他利率。不幸的是，罗斯达斯特（Rosstat）网站找不到相关的网站。这是一般财务分析文章中的最终出版物。

More articles:


All Articles