Get best of the week

三元计算机编程：玩模拟器

就像我说的那样，我正在缓慢地构建一个基于平衡三进制数系统的非常简单但功能强大且毫不妥协的三进制计算器。在本文中，我将介绍计算器的仿真器，这将有助于调试铁。如果您有兴趣，请不要犹豫为其编写程序，我一定会在准备好后立即在真实硬件上启动它们！这很简单，Triador理解通常的非常原始的命令式语言，类似于汇编器或Brainfuck ：）



-噩梦！零和一无处不在。看来我看到了一个平局。
“这只是一个梦想，班德。” 没有二。

, ! - , , !




, -13 +13. R1-R4 R5-R13. , R13 — , ( ). , 13 [-13..+13]. , / . 27 27 . , 729 . :





, , ( ).


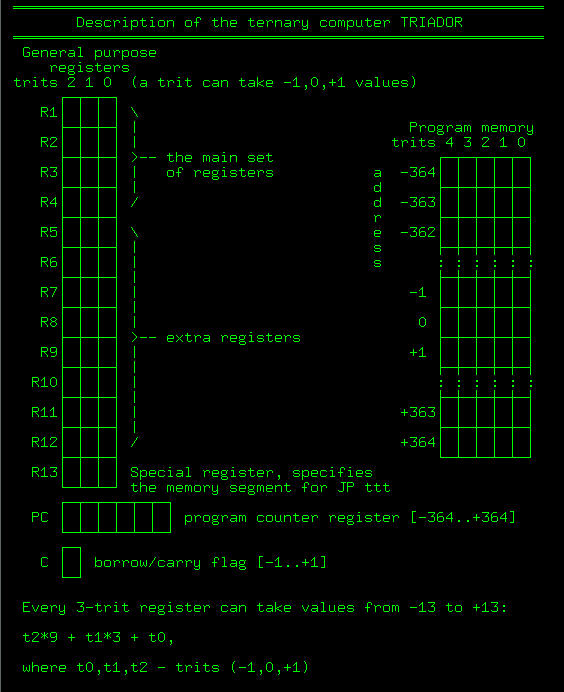
9 , . , EX ttt halt and catch fire. :





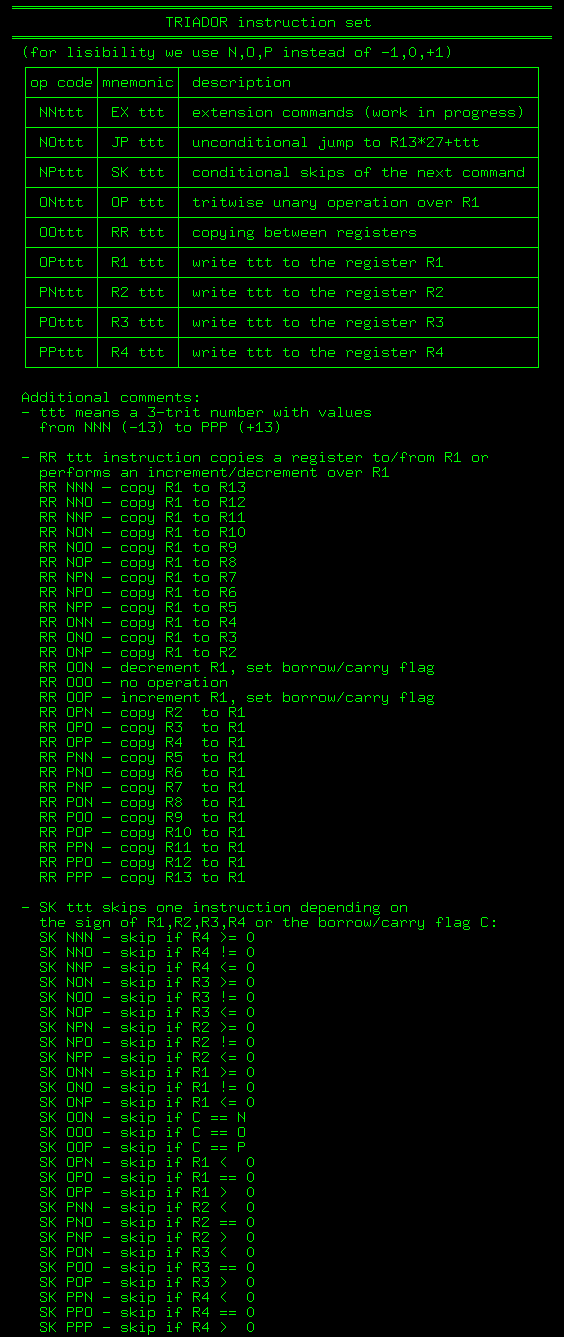
git clone https://github.com/ssloy/triador.git
cd triador
mkdir build
cd build
cmake ..
make
./triador ../prog/add.txt

:


在gitpod中打开


, . ( ).




. . . , , ttt NNN (-13) PPP (+13):


  • EX ttt
  • JP ttt
  • SK ttt
  • OP ttt
  • RR ttt
  • R1 ttt
  • R2 ttt
  • R3 ttt
  • R4 ttt

.




, . , , R1-R4.



, , R2 R3. ! /. ? !


. , R2 R3 . /, R2 R3 , R2 :


int main() {
    unsigned int R2 = 2;
    unsigned int R3 = 11;
    while (R2!=0) {
        R3++;
        R2--;
    }
    return R3;
}

, ? , , R2 :


int main() {
    int R2 = -2;
    int R3 = 13;
    while (R2!=0) {
        if (R2>0) R3++;
        if (R2<0) R3--;
        if (R2>0) R2--;
        if (R2<0) R2++;
    }
    return R3;
}

, , . . : / R1. , R3 , R1, , R1 R3!


, R2 R3 . R3:



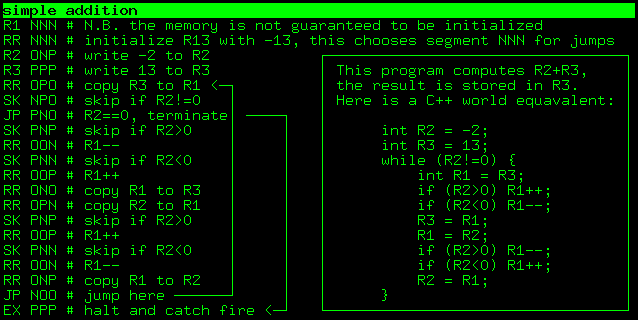
( ) — . NNN NNN, -364 . , , , .


:


$ ./triador ../prog/add.txt | tail -n 3
 R1  R2  R3  R4  R5  R6  R7  R8  R9 R10 R11 R12 R13  C   PC
 11   0  11   5   0   6 -12  -2  11   8  11 -10 -13  0  -345

, R3 11, -2 + 13.


, while , , JP, SK, .


: , JP ttt ttt, . ? R13! JP ttt 27*R13 + ttt. , ttt , R13. NNN (-13),


R1 NNN # write -13 to R1
RR NNN # copy R1 to R13

, R13, NNN.




, . , , . R2 R3, R3 R4: R3 + R4*27, , R4 -1, 0 or 1.



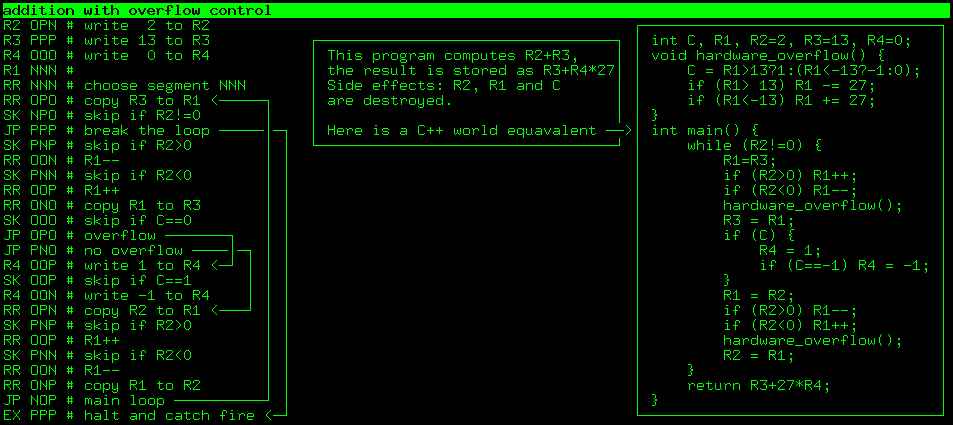
$ ./triador ../prog/add-with-overflow-control.txt |tail -n 3
 R1  R2  R3  R4  R5  R6  R7  R8  R9 R10 R11 R12 R13  C   PC
-12   0 -12   1  -9   2 -12  -6   4   5   6   7 -13  0  -338

, R3 + 27 * R4 15, 2+13. - R4 C:


[...]
SK OOO # skip if C==0        
JP OPO # overflow ───────┐   
JP PNO # no overflow ────│─┐ 
R4 OOP # write 1 to R4 <─┘ │ 
SK OOP # skip if C==1      │ 
R4 OON # write -1 to R4    │ 
RR OPN # copy R2 to R1 <───┘ 
[...]



, [-13..+13] ? , word ( , ). R1,R2 R3,R4. , R4,R5.



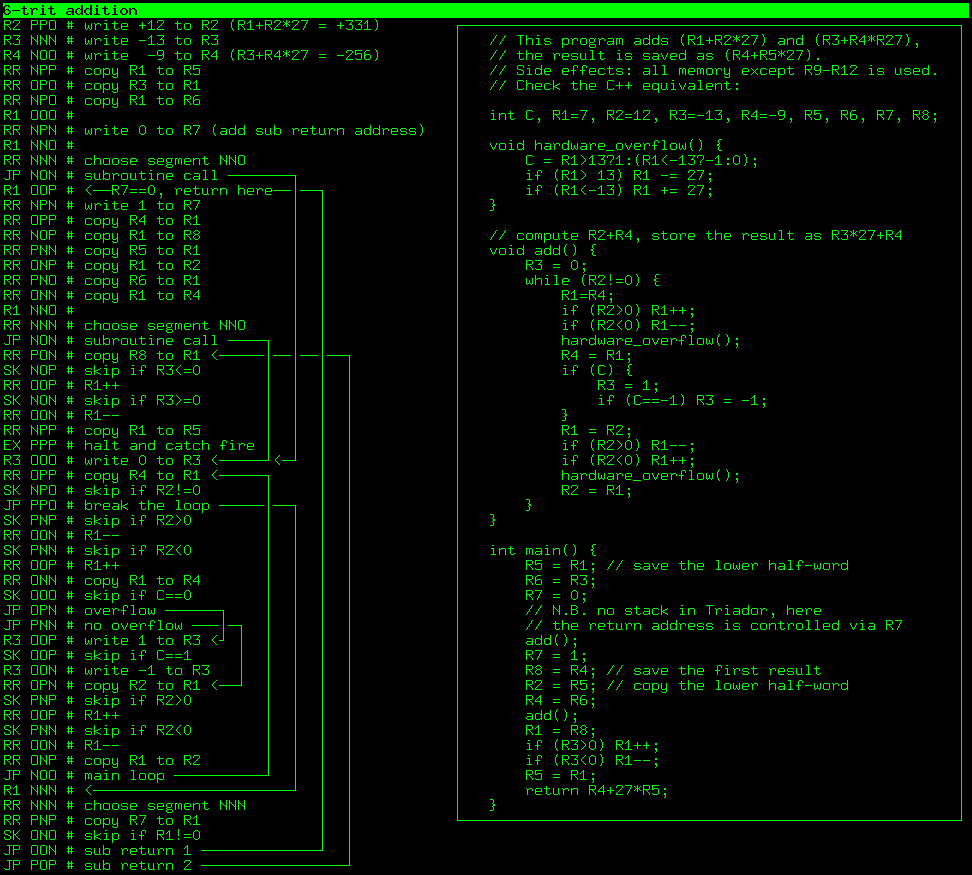
$ ./triador ../prog/long-add.txt |tail -n 3
 R1  R2  R3  R4  R5  R6  R7  R8  R9 R10 R11 R12 R13  C   PC
  3   0   0  -6   3 -13   1   3   6   5  13  -2 -13  0  -335

, R4+27 * R5 = 75, 331-256. , ? , , . , . , . , C++ :)


: , . , . ! R7 , -. , R7 :


[...]
SK ONO # skip if R1!=0
JP OON # sub return 1
JP POP # sub return 2



, . , R2 R3. R2.


, , C++. , R2 R3 , :


int main() {
    int R2 = 12, R3 = 8;

    while (true) {
        if (R2==R3) break;
        if (R2>R3)
            R2 = R2 - R3;
        else
            R3 = R3 - R2;
    }

    return R2;
}

, ? , : R2, R3; , . m R2 R3, , , R2-R3. , R2 = a m, R3 = b m , R2-R3 = (a-b) m. - .


, ? :) : , . , !


int main() {
    int R2 = 12, R3 = -8;

    while (true) {
        if (R2<0) R2 = -R2;
        if (R3>0) R3 = -R3;

        if (R2==-R3) break;

        int R4 = R2 + R3;
        if (R4>0)
            R2 = R4;
        else
            R3 = R4;
    }

    return R2;
}

:



:


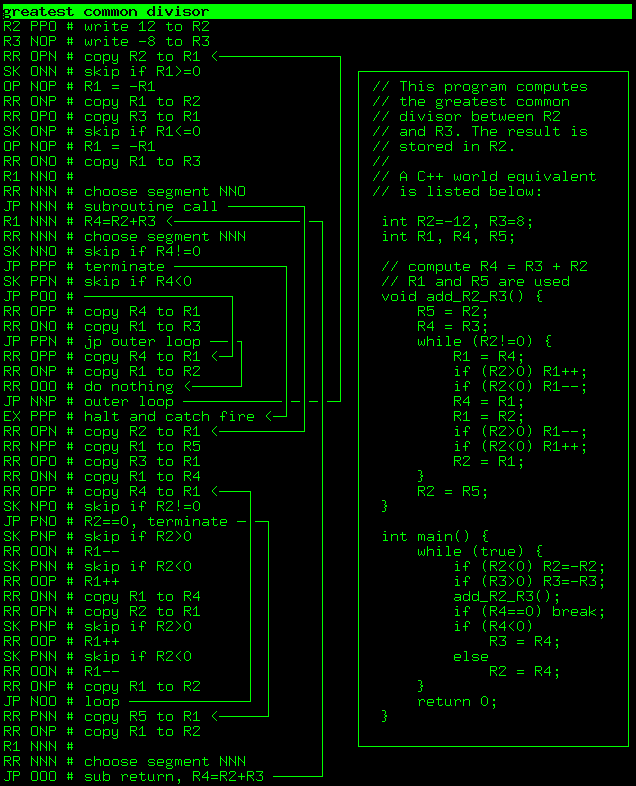
$ ./triador ../prog/gcd.txt |tail -n 3
 R1  R2  R3  R4  R5  R6  R7  R8  R9 R10 R11 R12 R13  C   PC
-13   4  -4   0   4  12  13   1  -7  -9   3   4 -13  0  -338

请注意，R2存储4，最大公因数是12和-8。



结论


对我的三元计算器进行编程并不比任何计算器（例如MK-61）困难，而且三位一体不会影响构建程序的原理。我的微型系列小说的第二季将专门研究算术逻辑设备的构造。同时，动荡不安使您无法用铁运动，可以用模拟器摆脱灵魂。提供解决上述任务的选项，提供有趣的新任务，让我们玩得开心！




敬请关注。

More articles:


All Articles