由于在寻找所需的错误的反向传播机制的解释时遇到了很大的困难,因此,我决定使用Word2Vec算法撰写有关错误的反向传播的文章。我的目标是使用简单但非平凡的神经网络来解释算法的本质。另外,word2vec在NLP社区中变得如此流行,以至于关注它会很有用。
这篇文章与我建议阅读的另一篇更实用的文章有关,它讨论了在Python中直接实现word2vec的方法。在这篇文章中,我们将主要集中在理论部分。
让我们从真正了解反向传播所需的东西开始。除了来自机器学习的概念(例如损失函数和梯度下降)之外,数学中的另外两个组件也派上用场:
如果您熟悉这些概念,那么进一步的考虑将很简单。如果尚未掌握它们,您仍然可以了解反向传播的基础知识。
首先,我要定义反向传播的概念,如果含义不够清楚,则将在以下段落中更详细地公开它。
1.什么是反向传播算法?
在神经网络的框架内,训练网络(即最小化损失函数)所涉及的唯一参数是权重(这里我指的是广义上的权重,指代权重和偏差)。权重在每次迭代中都会变化,直到我们达到损失函数的最小值为止。
, — , , .
, , .
, , , , w1 w2.

1. .
, w1 w2 .
, . , ∂ 大号/ ∂ 瓦特1 ∂ 大号/ ∂ 瓦特2, , . η, .
2. Word2Vec
word2vec, , , . , word2vec, NLP.
, word2vec [N, 3], N - , . , , '', , ( ), , ''. , word2vec .
word2vec : (CBOW) (skip-gram). , CBOW, , skip-gram.
. , woed2vec .
3. CBOW
CBOW . , :
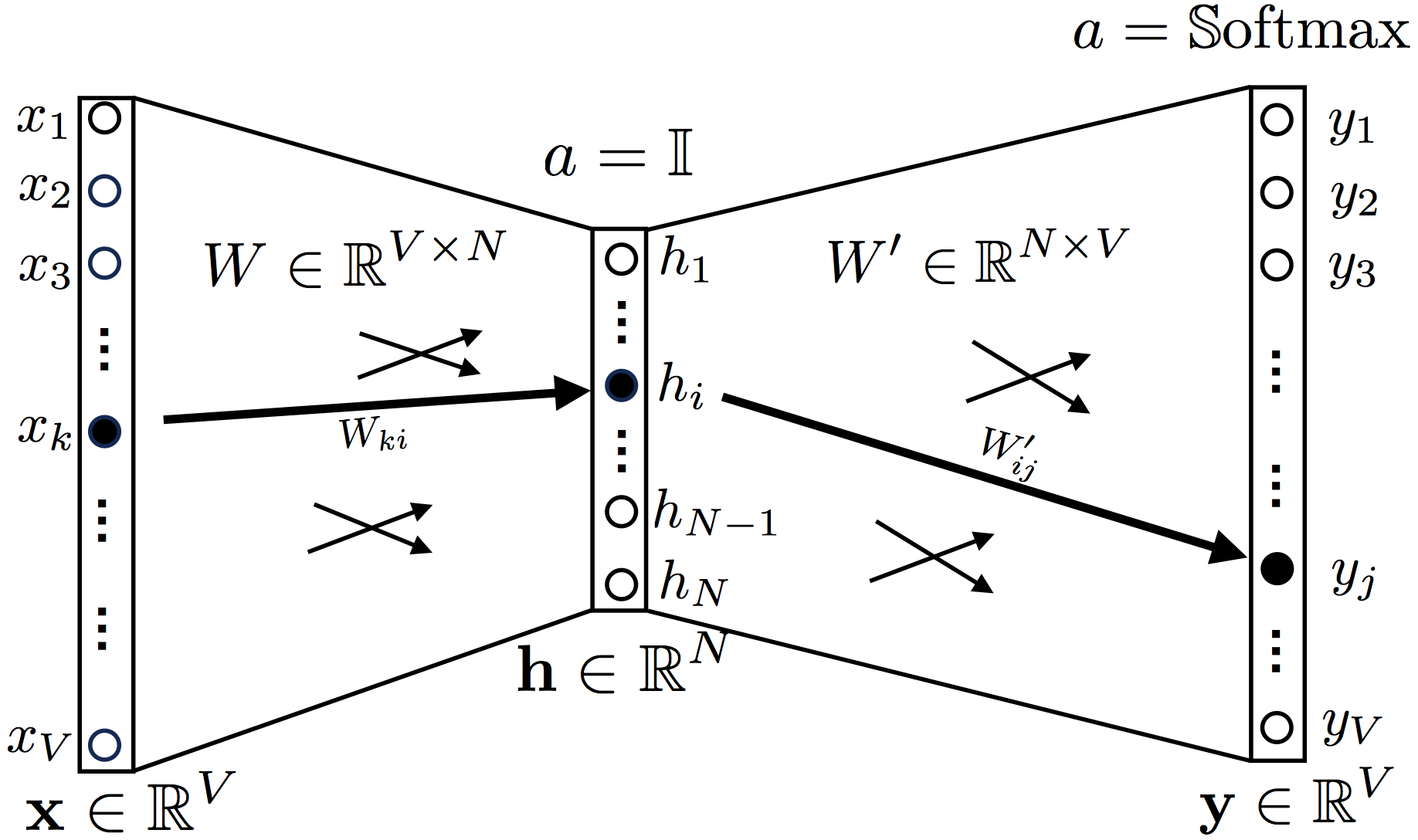
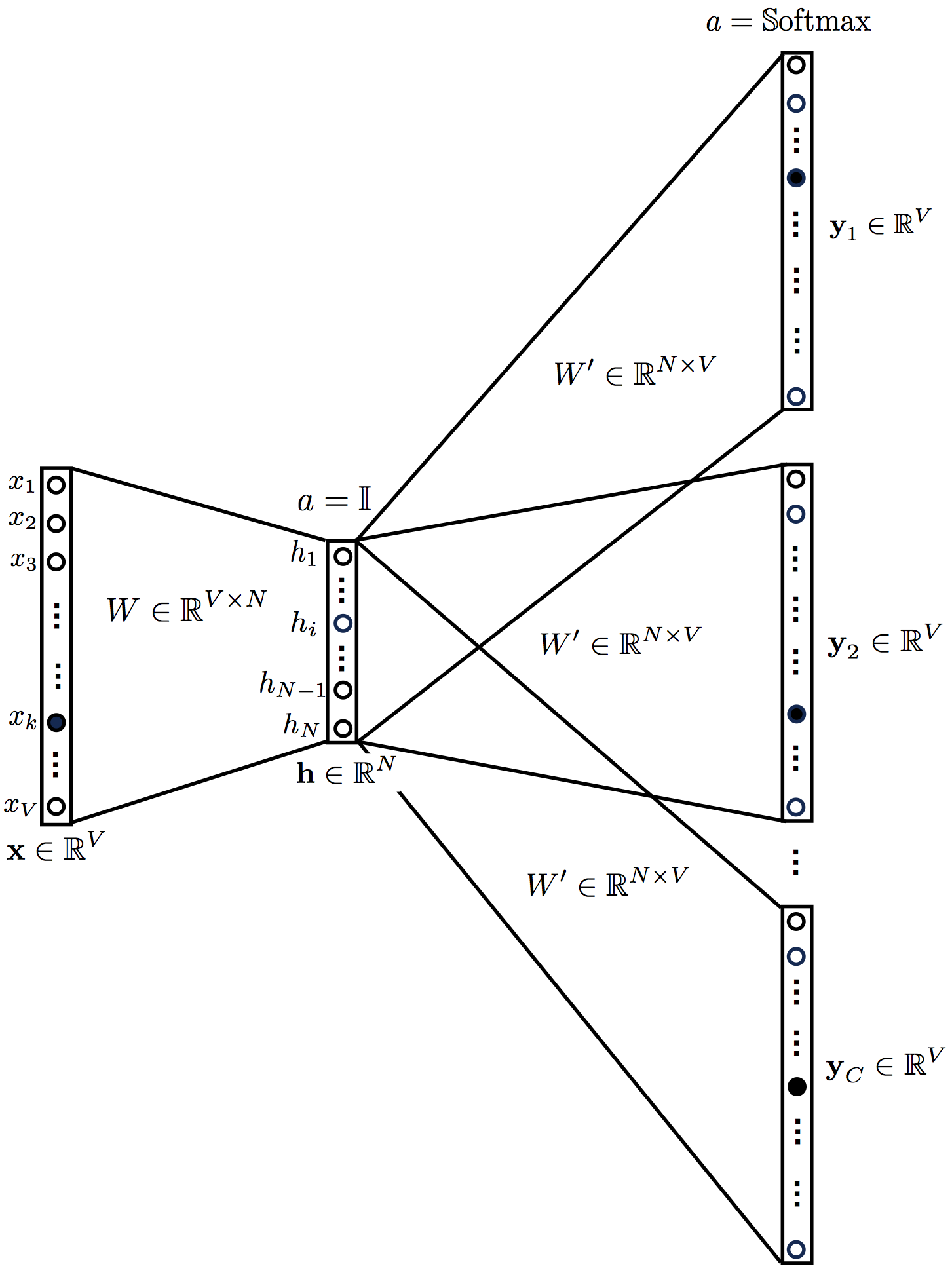
2. Continuous Bag-of-Words
, ,
a = 1 (identity function, , ).
Softmax.
one hot encoding , , , , , 1.
: ['', '', '', '', '', '']
OneHot('') = [0, 0, 0, 1, 0, 0]
OneHot(['', '']) = [1, 0, 0, 1, 0, 0]
OneHot(['', '', '']) = [1, 0, 0, 0, 1, 1]
, W V × Ñ, W ′ N × V, V — , N — ( , word2vec)
y t, , , , , .
, .
, word2vec :
"I like playing football"
CBOW (2) .
, 4 , V=4, , N=2, :
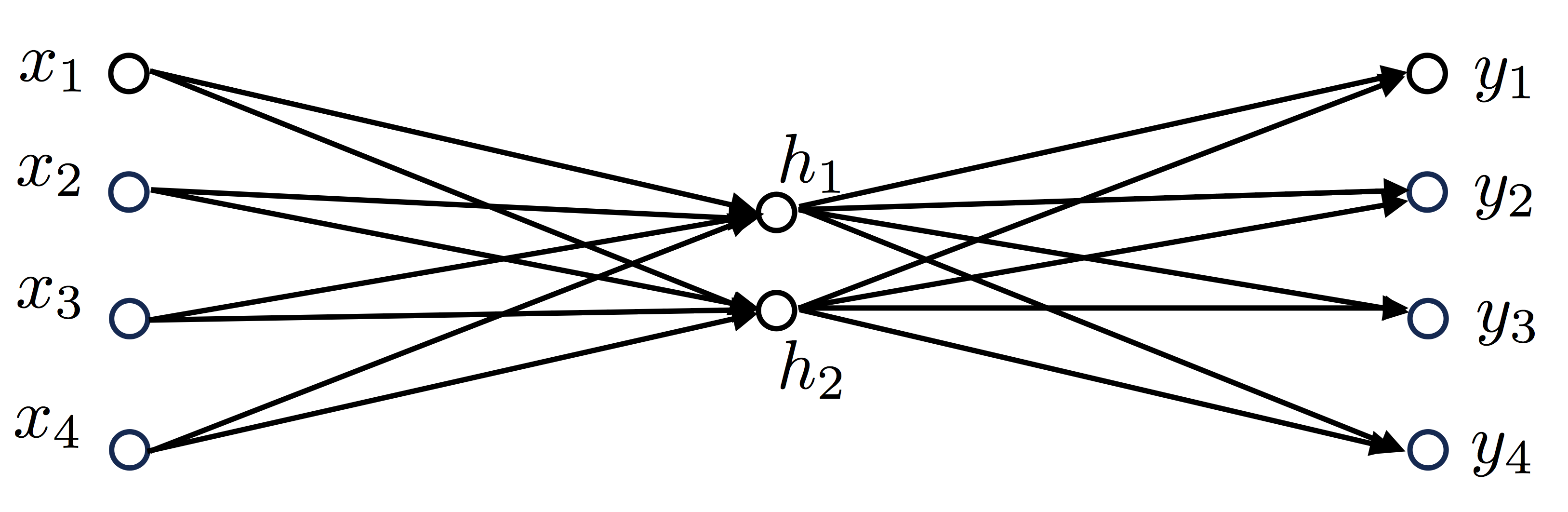
:
Vocabulary=[“I”,“like”,“playing”,“football”]
'' '' , . :

:
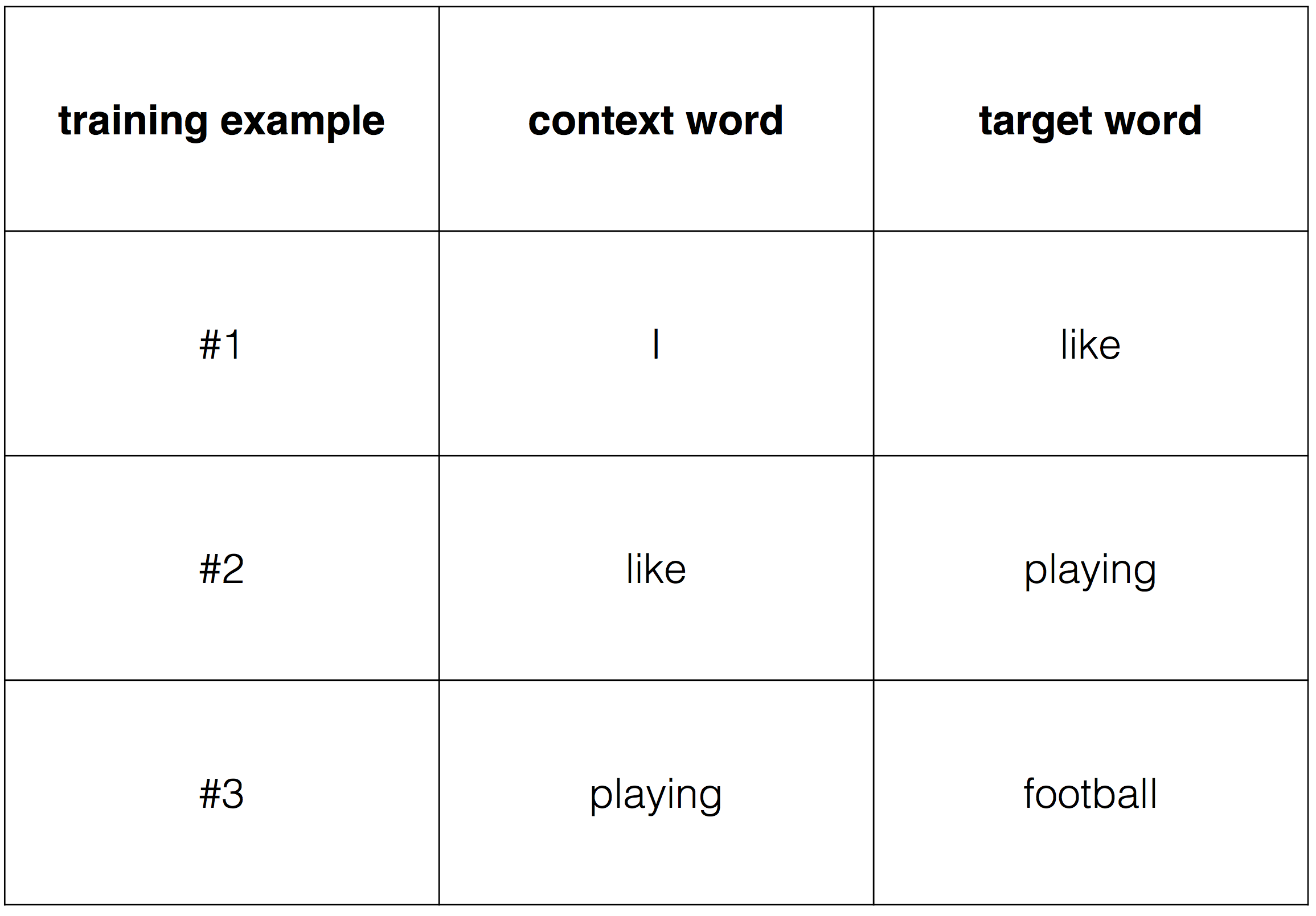
, one-hot encoding.
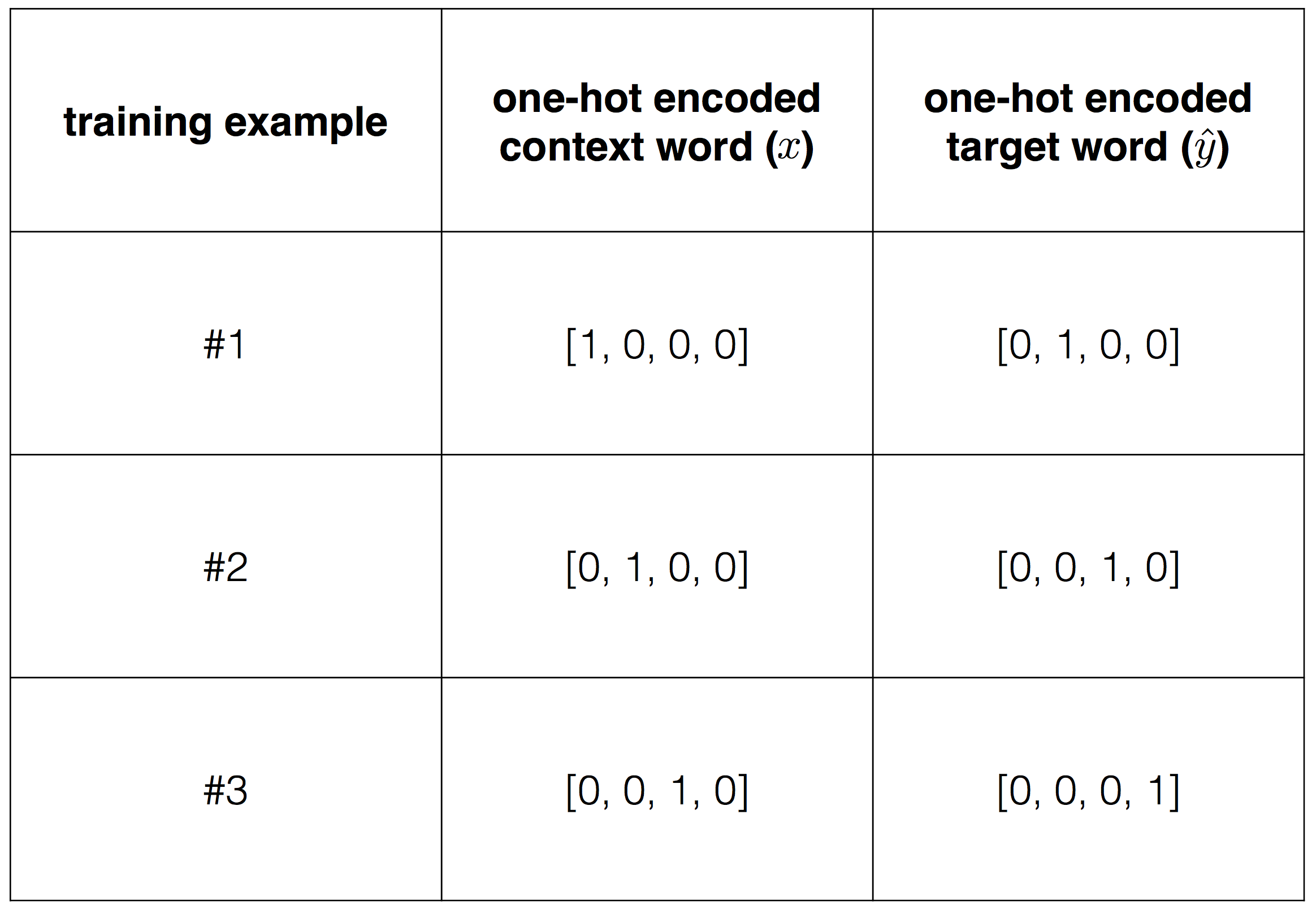
, , , . , , .
3.1 (Loss function)
1, , x:
h = W T xû = w ^ ' Ť ħ = w ^ ' Ť W¯¯ Ť Xÿ = š oftmax(Û)= 小号oftmax(w ^ ' Ť W¯¯ Ť X)
, h — , u — , y — .
, , , (wt, wc). , onehot encoding .
, onehot wt ( ).
softmax , :
, j* — .
. (1):
.
"I like play football", , "I" "like", , X=(1个,0,0,0) — "I", ˆÿ=(0,1个,0,0), "like".
word2vec, . W 4×2
w ^=(--1.381187280.548493730.39389902--1.1501331--1.169676280.360780220.06676289--0.14292845)
w ^′ 2×4
w ^′=(1.39420129--0.894417570.998696670.444470370.69671796--0.233643410.21975196--0.0022673)
"I like" :
H=w ^ŤX=(--1.381187280.54849373)
ü=w ^′ŤH=(--1.543507651.10720623--1.25885456--0.61514042)
ÿ=小号最大流量(ü)=(0.052565670.74454790.069875590.13301083)
ÿ,
大号=--日志P(“喜欢”|“一世”)=--日志ÿ3=--日志(0.7445479)=0.2949781。
, (1):
大号=--ü2+日志4∑一世=1个ü一世=--1.10720623+日志[经验值(--1.54350765)+经验值(1.10720623)+经验值(--1.25885456)+经验值(--0.61514042)]=0.2949781。
, "like play", , .
3.2 CBOW
, , W W` . , .
. (1) W W`. ∂L/∂W ∂L/∂W′
, . (1) W W`, u=[u1, ...., uV],
:
, (2) (3) .
(2), Wij, W, i j , uj ( yj).
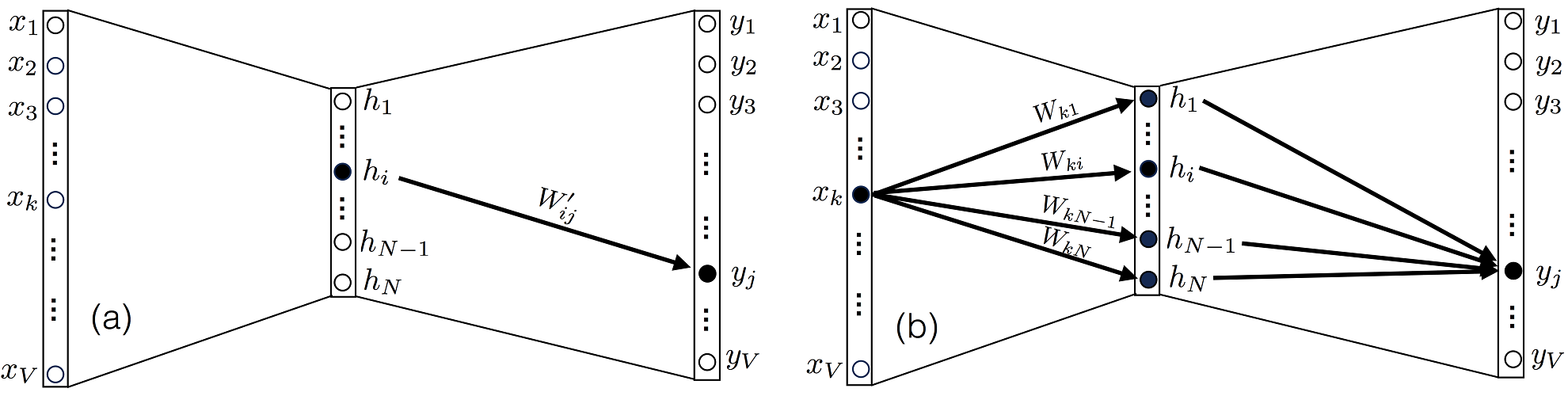
3. (a) yj hi W′ij W′. (b) , xk N Wk1…WkN W.
, ∂uk/∂W′ij, , k=j, 0.
(4):
∂L/∂uj, (5):
, δjj∗ — , , 1, , 0 .
(5) e N ( ), , , .
(4) (6):
(5) (6) (4) (7):
∂L/∂Wij, Xk, yj j W , 3(b). . ∂uk/∂Wij, uk u :
∂uk/∂Wij, l=i m=j, (8):
(5) (8) , (9):
. (7) (9) . (7)
⊗ .
(9) :
3.3
, (7) (9), , . . η>0, :
Wnew=Wold−η∂L∂WW′new=W′old−η∂L∂W′
3.4
. , . , . , . , , , .
4. CBOW
CBOW . . (4) . OneHot Encoded . word2vec. .

4. CBOW
CBOW CBOW .
h=1CWTC∑c=1x(c)=WT¯xu=W′Th=1CC∑c=1W′TWTx(c)=W′TWT¯xy= Softmax(u)=Softmax(W′TWT¯x)
, '' ¯x=∑Cc=1x(c)/C
, . :
, :
CBOW , , . W′ij
Wij:
:
(17) (18) .
(17) :
(18):
, CBOW .
⊗ .
5. Skip-gram
CBOW, , . :
5. Skip-gram .
skip-gram :
h=WTxuc=W′Th=W′TWTxc=1,…,Cyc= Softmax(u)=Softmax(W′TWTx)c=1,…,C
( uc) , y1=y2⋯=yC. :
L=−logP(wc,1,wc,2,…,wc,C|wo)=−logC∏c=1P(wc,i|wo)=−logC∏c=1exp(uc,j∗)∑Vj=1exp(uc,j)=−C∑c=1uc,j∗+C∑c=1logV∑j=1exp(uc,j)
skip-gram C×V
:
:
∂L/∂uc,j, :
CBOW :
Wij , :
, skip-gram :
(21):
(22):
6.
word2vec. . [2] ( softmax, negative sampling), . [1].
, word2vec.
下一步是用您喜欢的编程语言实现这些方程式。如果您喜欢Python,我已经在下一篇文章中实现了这些等式。
希望在那里见到你!
网站连结
[1] X. Rong,《word2vec参数学习解释》,arXiv:1411.2738(2014)。
[2] T. Mikolov,K。Chen,G。Corrado,J。Dean,向量空间中单词表示的有效估计,arXiv:1301.3781(2013年)。