Coderik曾经指出:“永远不会有很多卡尔曼滤波器。” 贝叶斯定理也可以这样说,因为一方面它是如此简单,另一方面却很难理解其深度。

YouTube拥有一个很棒的Student Dave频道,但是最后一个视频是六年前发布的。该频道包含教育视频,其中的作者以非常简单的语言讲述了复杂的事情:贝叶斯定理,卡尔曼滤波器等。学生戴夫(Student Dave)用matlab中的计算示例来补充他的故事。
他的视频课程“迭代贝叶斯评估”确实对我有很大帮助(在频道上,它对应于播放列表“迭代贝叶斯评估:使用MATLAB”)我希望每个人都熟悉Dave的解释,但不幸的是该项目不受支持。戴夫本人没有联系。您无法将翻译添加到视频中,因为作者本人必须将其启动。与youtube联系并没有得到结果,因此我决定在一篇俄语文章中描述该材料,并在最受关注的地方发布。由于经历了我的主观理解,因此对该材料进行了大量的修订和补充,因此将其作为翻译将是不合适的。但是我非常听从Dave的解释。我用python重写了它的代码,因为我自己在其中工作,并认为它是数学软件包的良好替代品。
因此,如果您想对贝叶斯定理的主题有更深入的了解,欢迎您。
问题的提法
, “ ”. .

-, . , . , . . , . . - .
- . . . .

( ) () .
.
, .
fposterior(x)— ;
fprior(x)— ;
fmes(x)— ( Lx(sample)).
. , ( , ):
fmes(x)=pdf(x=y,μ=x,σ=σ)=12πσe−(y−x)22σ2,
pdf— ;
μ— ;
σ— ;
y— .
(N), , .
.

.
σ, 99,7 %.
. -.
(3,5). ( ) .
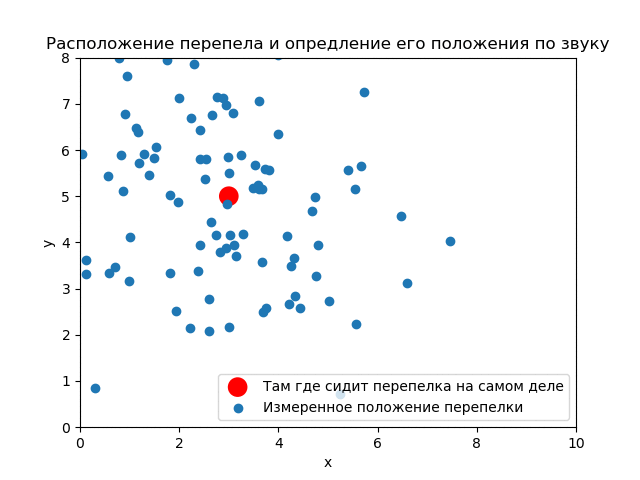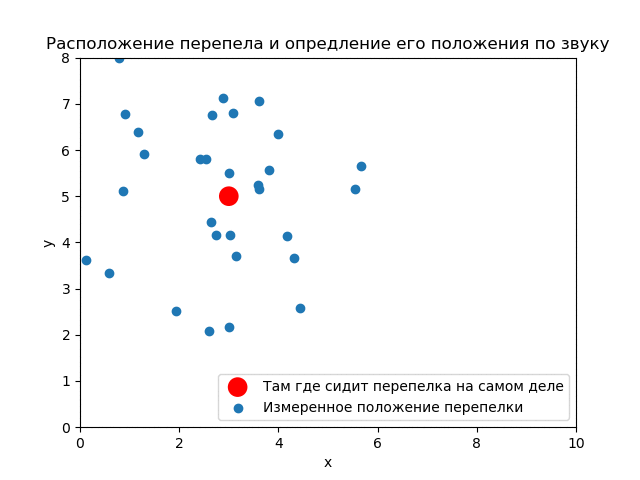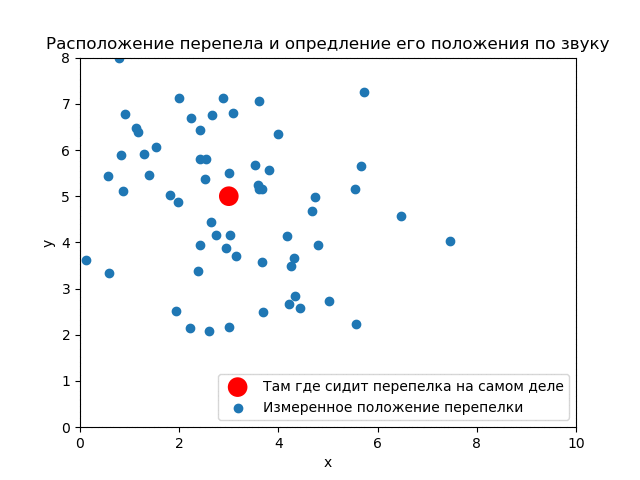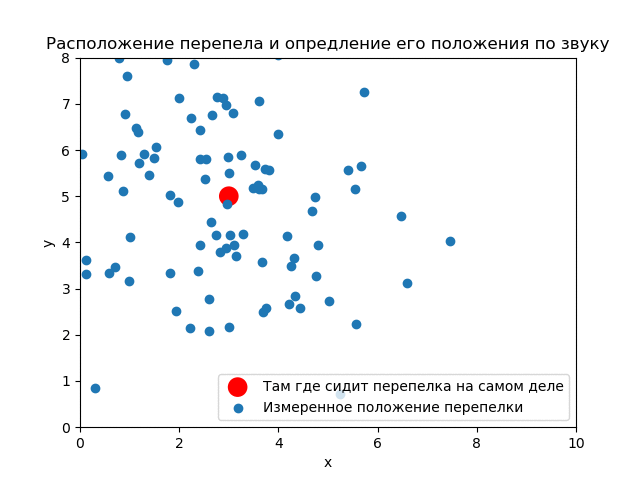
() , . .
:
fposterior(X)=fprior(X)⋅f(X)∫fprior(X)⋅fmes(X)dX,
X— (xy);
fposterior(X)— ;
fprior(X)— ;
fmes(X)— .
:
fmes(X)=1(2π)2detKe12(Y−X)TK−1(Y−X),
K— ;
Y— (xy).
, .
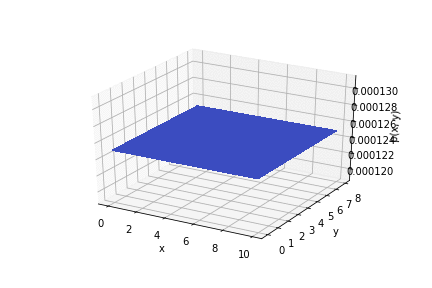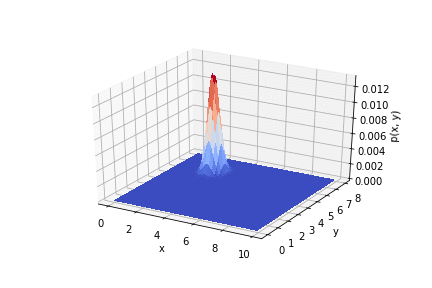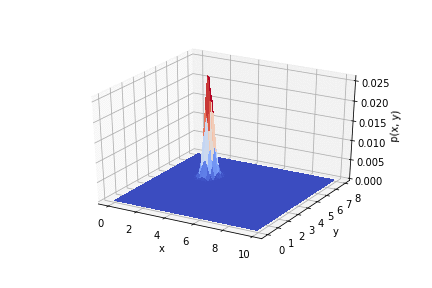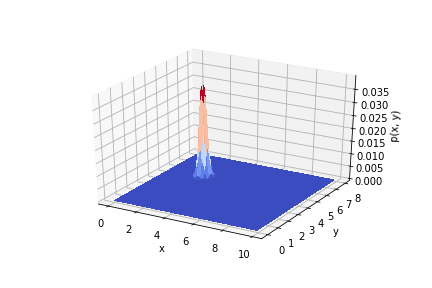
.
因此,可以看到实验结果如何影响先验分布。如果正确使用测量值,则可以得到良好的精度。
但是,仅查找所有测量值的平均值来评估鹌鹑的位置,难道不是很容易吗?当然。这个例子只是连续随机变量的贝叶斯定理的一个很好的例子。本文旨在解决这一理论。
在这几周的自我隔离中,请在戴夫海峡(Dave Channel)停留。对所有人都好。