👴🏾 🤽🏿 ♐️ 朱莉娅与量子计算 🐖 🌗 ⛹🏼

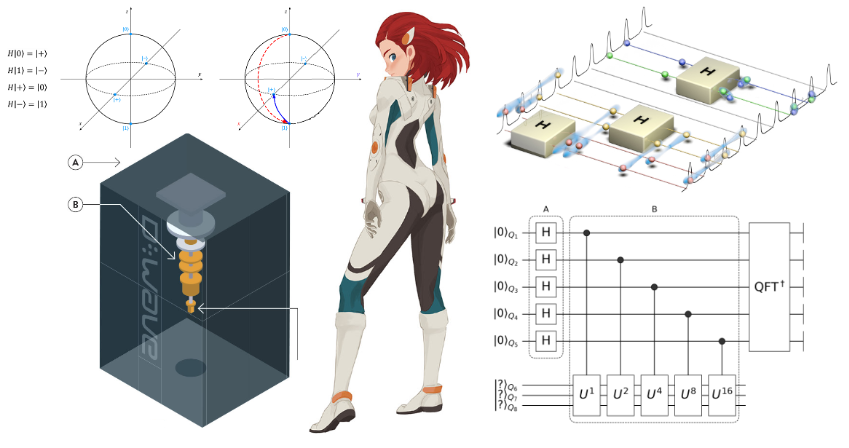
我们提出了Yao（文章），它是一个开放源码的Julia软件包，用于解决量子计算研究中的实际问题。姚（Yao）这个名字来自第一个汉字，表示统一性（幺正）。

Yao? , , , Julia. , :

Julia ( Zygote), , , . , , .. , !

(AD) : - . AD , – , .

Yao - (AD), . . AD

n, d = 16, 100
circuit = dispatch!(variational_circuit(n, d),:random);
h = heisenberg(n)

@time for i in 1:100
     _, grad = expect'(h, zero_state(n) => circuit)
     dispatch!(-, circuit, 1e-1 * grad)
     println("Step $i, energy = $(real.(expect(h, zero_state(n)=>circuit)))")
end

100- (4816 ), 16- . AD , Zygote, (). , . .

. . , , .

-, - ( , QBIR) . Yao , , . , , , CUDA CuYao , Julia CUDAnative. Yao SymEngine, .

-, Julia, Yao . Yao ( CUDA- CuYao) — -, . .

, , . , , .

, , Yao .

?

, .
(, OpenQASM), (YaoIR), , ( ) !

- , , . , , !

Julia.

] dev https://github.com/QuantumBFS/QuAlgorithmZoo.jl.git

using Pkg
pkgs = ["Plots", "Flux", "Yao", "YaoExtensions", "StatsBase", "BitBasis", "FFTW", "SymEngine"]

for p in pkgs
    Pkg.add(p)
end

using Yao, YaoExtensions, Plots, StatsBase

--

GHZ — , ( ). , :

—
: 2 — ( )
— , , Q#

— . - , , , , . : , , — , .
. , . — . , , , , . , , , , , , - .
. . . — ( ).
Quirk —

: , , . , IBM , , , .

, , , ! , - :

| G H Z ⟩ = \frac{1}{\sqrt{d}} \sum_{i = 0}^{d - 1} | i ⟩ \otimes \dots \otimes | i ⟩ = \frac{1}{\sqrt{d}} (| 0 ⟩ \otimes \dots \otimes | 0 ⟩ + \dots + | d - 1 ⟩ \otimes \dots \otimes | d - 1 ⟩)

$|\mathrm {GHZ} \rangle ={\frac {1}{\sqrt {d}}}\sum _{i=0}^{d-1}|i\rangle \otimes \cdots \otimes |i\rangle ={\frac {1}{\sqrt {d}}}(|0\rangle \otimes \cdots \otimes |0\rangle +\cdots +|d-1\rangle \otimes \cdots \otimes |d-1\rangle )$

Yao:

circuit = chain(
    4,
    put(1=>X),
    repeat(H, 2:4),
    control(2, 1=>X),
    control(4, 3=>X),
    control(3, 1=>X),
    control(4, 3=>X),
    repeat(H, 1:4),
)

nqubits: 4
chain
├─ put on (1)
│  └─ X gate
├─ repeat on (2, 3, 4)
│  └─ H gate
├─ control(2)
│  └─ (1,) X gate
├─ control(4)
│  └─ (3,) X gate
├─ control(3)
│  └─ (1,) X gate
├─ control(4)
│  └─ (3,) X gate
└─ repeat on (1, 2, 3, 4)
   └─ H gate

, : X, not-gate ( ), , cnot-.
(, )

results = ArrayReg(bit"0101") |> circuit |> r->measure(r, nshots=1000)

hist = fit(Histogram, Int.(results), 0:16)
bar(hist.edges[1] .- 0.5, hist.weights, legend=:none)

, - $\mid 0100 \rangle$ $\mid 1011 \rangle$ .

— :

N = 2^{n} Q F T ∣ x ⟩ = \frac{∥ x ∥}{2^{n / 2}} \sum_{y = 0}^{2^{n} - 1} \exp (2 π i \frac{x y}{N}) ∣ y ⟩

$N = 2^n \\ QFT\mid x \rangle = \frac{\parallel x \parallel }{2^{n/2}}\sum_{y=0}^{2^n-1} \exp\left( 2\pi i \frac{xy}{N} \right) \mid y \rangle$

R_{k} = (\begin{matrix} 1 & 0 \\ 0 & e^{2 π i} / 2^{k} \end{matrix})

$R_k = \begin{pmatrix} 1 & 0\\ 0 & e^{2\pi i}/2^k \end{pmatrix}$

, .

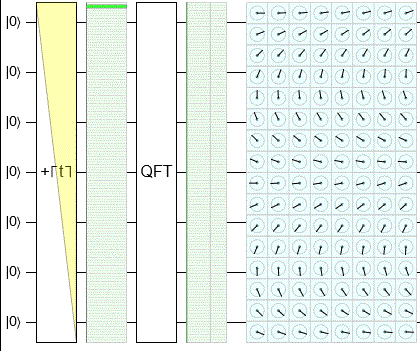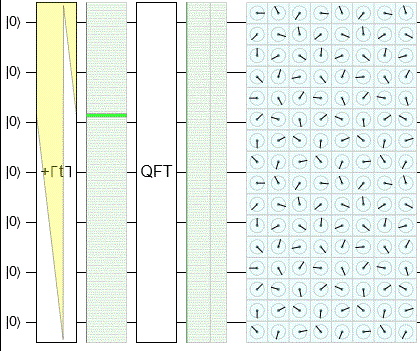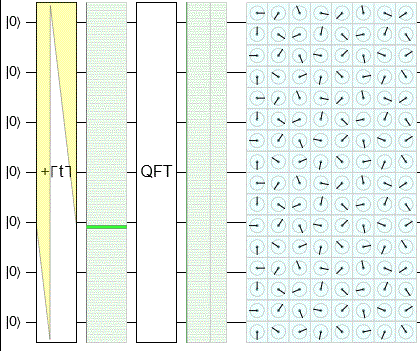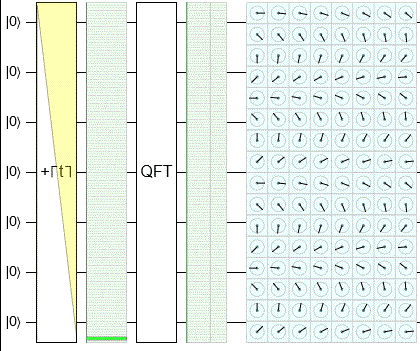
(QFT) , :

B (A ):

A(i, j) = control(i, j=>shift(2π/(1<<(i-j+1))))
R4 = A(4, 1)

# (n -> control(n, 4, 1 => shift(0.39269908169872414)))

, , mat. A $R_4$ :

R4(5)

#nqubits: 5
#control(4)
#└─ (1,) shift(0.39269908169872414)

mat(R4(5))

32×32 LinearAlgebra.Diagonal{Complex{Float64},Array{Complex{Float64},1}}:
 1.0+0.0im      ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅      1.0+0.0im      ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅      1.0+0.0im      ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅      1.0+0.0im         ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
    ⋮                                        ⋱     ⋮                         
     ⋅          ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅      …      ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅              ⋅         
     ⋅          ⋅          ⋅          ⋅      …  1.0+0.0im          ⋅         
     ⋅          ⋅          ⋅          ⋅             ⋅      0.92388+0.382683im

i- , i- B. , n, k- .

, B

B(n, k) = chain(n, j==k ? put(k=>H) : A(j, k) for j in k:n)

qft(n) = chain(B(n, k) for k in 1:n)
qft(4)

nqubits: 4
chain
├─ chain
│  ├─ put on (1)
│  │  └─ H
│  ├─ control(2)
│  │  └─ (1,) shift(1.5707963267948966)
│  ├─ control(3)
│  │  └─ (1,) shift(0.7853981633974483)
│  └─ control(4)
│     └─ (1,) shift(0.39269908169872414)
├─ chain
│  ├─ put on (2)
│  │  └─ H
│  ├─ control(3)
│  │  └─ (2,) shift(1.5707963267948966)
│  └─ control(4)
│     └─ (2,) shift(0.7853981633974483)
├─ chain
│  ├─ put on (3)
│  │  └─ H
│  └─ control(4)
│     └─ (3,) shift(1.5707963267948966)
└─ chain
   └─ put on (4)
      └─ H

, A B , , , , .

-, PrimitiveBlock, QFT. , CompositeBlock.

struct QFT{N} <: PrimitiveBlock{N} end
QFT(n::Int) = QFT{n}()
#  
circuit2(::QFT{N}) where N = qft(N)
#     
YaoBlocks.mat(::Type{T}, x::QFT) where T = mat(T, circuit2(x))
YaoBlocks.print_block(io::IO, x::QFT{N}) where N = print(io, "QFT($N)")

using FFTW, LinearAlgebra

function YaoBlocks.apply!(r::ArrayReg, x::QFT)
    α = sqrt(length(statevec(r)))
    invorder!(r)
    lmul!(α, ifft!(statevec(r)))
    return r
end

print_block , QFT . , ,

r = rand_state(5)
r1 = r |> copy |> QFT(5)
r2 = r |> copy |> circuit2(QFT(5))
r1 ≈ r2

# true

, , .

. , , ( ). L . , ver Val(:quantum) Val(:classical), .

using Yao, BitBasis
using YaoExtensions: KMod, QFTCircuit
using QuAlgorithmZoo: NumberTheory

function shor(L::Int, ver=Val(:quantum); maxtry=100)
    L%2 == 0 && return 2

    # find short cut solutions like `a^b`
    res = NumberTheory.factor_a_power_b(L)
    res !== nothing && return res[1]

    for i in 1:maxtry
        # step 1
        x = NumberTheory.rand_primeto(L)

        # step 2
        r = get_order(ver, x, L; )
        if r%2 == 0 && powermod(x, r÷2, L) != L-1
            # step 3
            f1, f2 = gcd(powermod(x, r÷2, L)-1, L), gcd(powermod(x, r÷2, L)+1, L)
            if f1!=1
                return f1
            elseif f2!=1
                return f2
            else
                error("Algorithm Fail!")
            end
        end
    end
end

, :

, L, . . gcd(x, L) == 1. .
x, . . r, mod(x^r, L) == 1. r , x^(r÷2) , , . , L-1 (mod L).
5.2 ,
- gcd(x^(r÷2)-1, L) gcd (x^(r÷2)+1, L) (!=1) L. , powermod(x, r÷2, L) -1, 1, r/2 .

— . NumberTheory, .

,
s / r. , , .

- nshot, nbit ( ) ncbit ( ). nbit , ncbit

"""    ."""
estimate_ncbit(nbit::Int, ϵ::Real) = 2*nbit + 1 + ceil(Int,log2(2+1/2ϵ))

get_order(::Val{:classical}, x::Int, L::Int; kwargs...) = NumberTheory.find_order(x, L)
function get_order(::Val{:quantum}, x::Int, L::Int; nshots::Int=10,
            nbit::Int=bit_length(L-1), ncbit::Int=estimate_ncbit(nbit, 0.25))
    c = order_finding_circuit(x, L; nbit=nbit, ncbit=ncbit)
    reg = join(product_state(nbit, 1), zero_state(ncbit))

    res = measure(copy(reg) |> c; nshots=nshots)
    for r in res
        # split bit string b into lower bits `k` and higher bits `r`.
        mask = bmask(1:ncbit)
        k,i = r&mask, r>>ncbit
        # get s/r
        ϕ = bfloat(k)  #
        ϕ == 0 && continue

        # order_from_float: given a floating point number,
        # return the closest rational number with bounded number of continued fraction steps.
        order = NumberTheory.order_from_float(ϕ, x, L)
        if order === nothing
            continue
        else
            return order
        end
    end
    return nothing
end

order_finding_circuit(x::Int, L::Int; nbit::Int=bit_length(L-1), ncbit::Int=estimate_ncbit(nbit, 0.25)) -> AbstractBlock

x L,
|1>⊗|0> "" .

function order_finding_circuit(x::Int, L::Int; nbit::Int, ncbit::Int)
    N = nbit+ncbit
    chain(N, repeat(N, H, 1:ncbit), KMod{N, ncbit}(x, L),
        subroutine(N, qft_circuit(ncbit)', 1:ncbit))
end

KMod mod(a^k*x, L).
k — , k ( ncbit) , N-K a. , , , Yao. , , .
.

, - - :

@time shor(35, Val(:quantum))

# 2.287219 seconds (14.37 k allocations: 113.341 MiB, 1.38% gc time)
# 5

@time shor(35, Val(:classical))
# 0.000208 seconds (6 allocations: 224 bytes)
# 5

, . : , , .. , , .

, , .

朱莉娅与量子计算

?

--

More articles: