Get best of the week

以Sberbank的优先股和普通股为例比较python中两只股票的报价动态

您好，今天我想谈谈我在分析Sberbank股票方面的经验。有时它们显示出稍微不同的动态-分析它们的报价变化对我来说变得很有趣。

在此示例中，我们将从Finam网站下载报价。链接下载常规的Sberbank。

对于列操作，我将使用pandas进行matplotlib可视化。

我们导入：

import pandas as pd
import matplotlib.pyplot as plt

为防止表缩小，您必须删除限制：

pd.set_option('display.max_columns', None)
pd.set_option('display.expand_frame_repr', False)
pd.set_option('max_colwidth', 80)
pd.set_option('max_rows', 6000)

读取库存数据


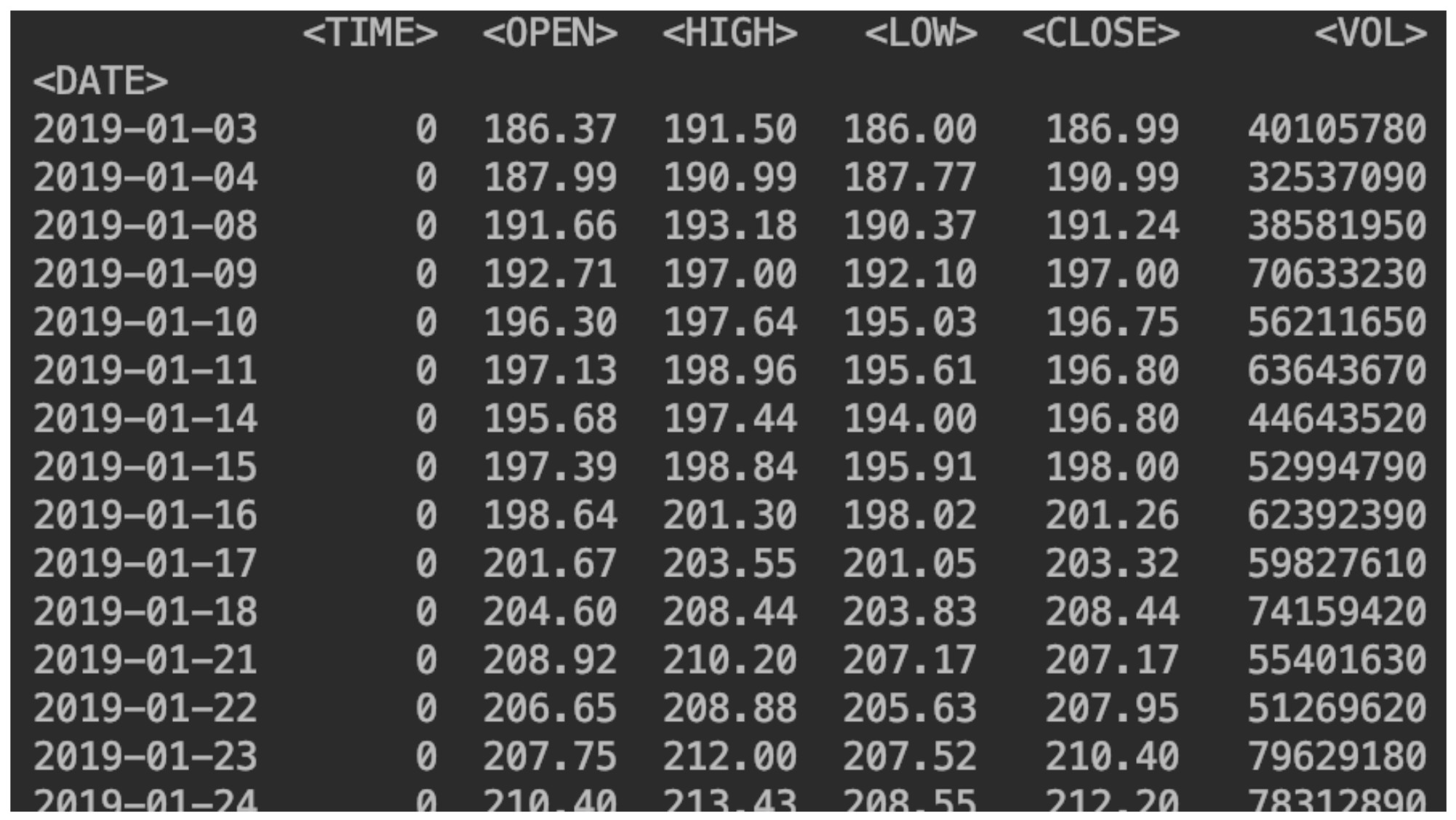
df = pd.read_csv("SBER_190101_200105.csv",sep=';', header=0, index_col='<DATE>', parse_dates=True)

（指定分隔符，列名位于此位置，哪一列将作为索引，启用日期解析）。

同时指出排序方式：

df = df.sort_values(by='<DATE>')

我们显示我们的数据：

print(df)



添加价格变动的列

df['returns']=(df['<CLOSE>']/df['<CLOSE>'].shift(1))-1

因此可以精确得出百分比：

df['returns_pers']=((df['<CLOSE>']/df['<CLOSE>'].shift(1))-1)*100



添加第二个份额


完全一样地做。

df2 = pd.read_csv("SBERP_190101_200105.csv",sep=';', header=0, index_col='<DATE>', parse_dates=True)

df = df.sort_values(by='<DATE>')

df2['returns_pers']=((df2['<CLOSE>']/df2['<CLOSE>'].shift(1))-1)*100
df2['returns']=(df2['<CLOSE>']/df2['<CLOSE>'].shift(1))-1
print(df2)

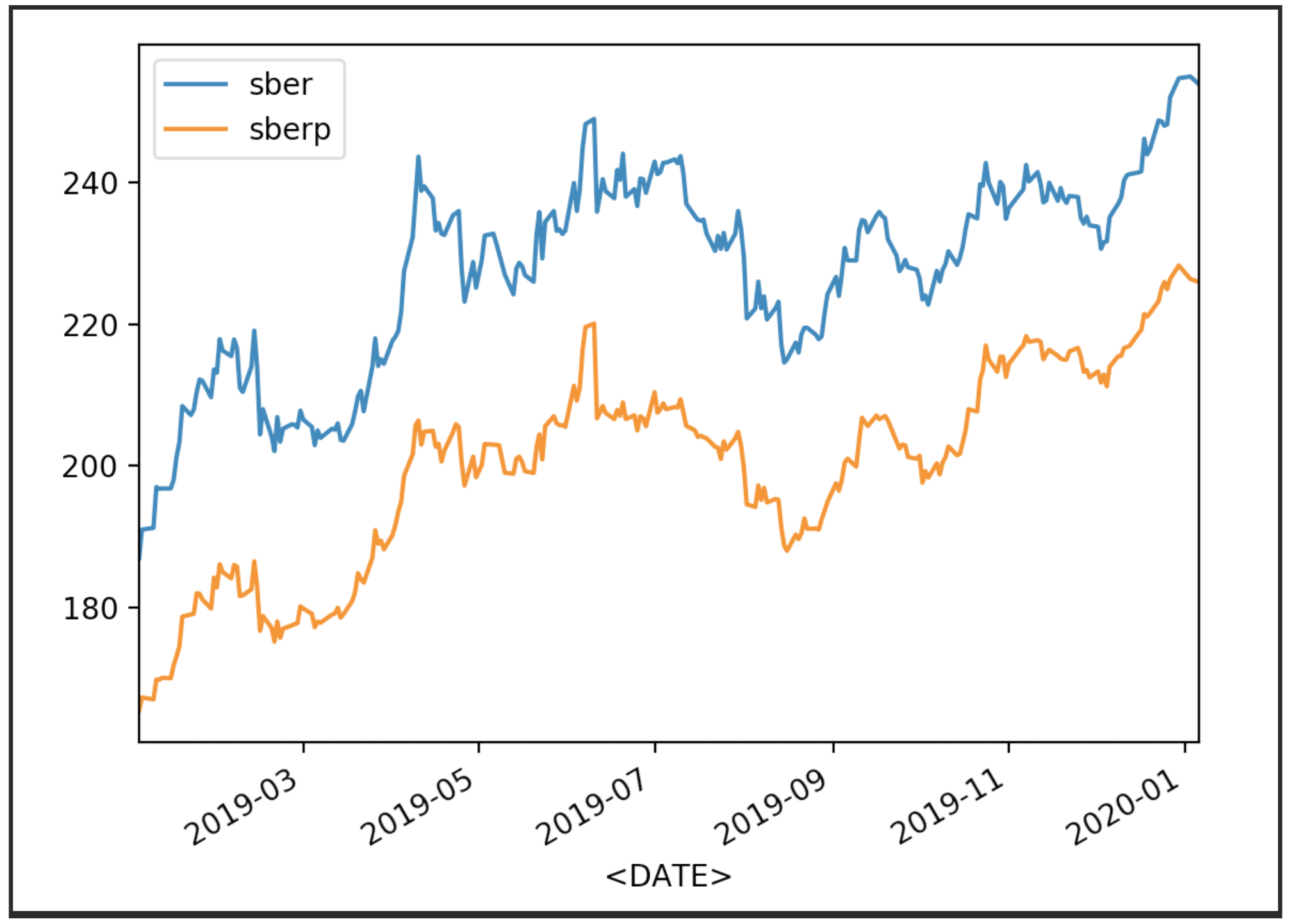
我们可视化我们的股票报价


df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
plt.legend()
plt.show()



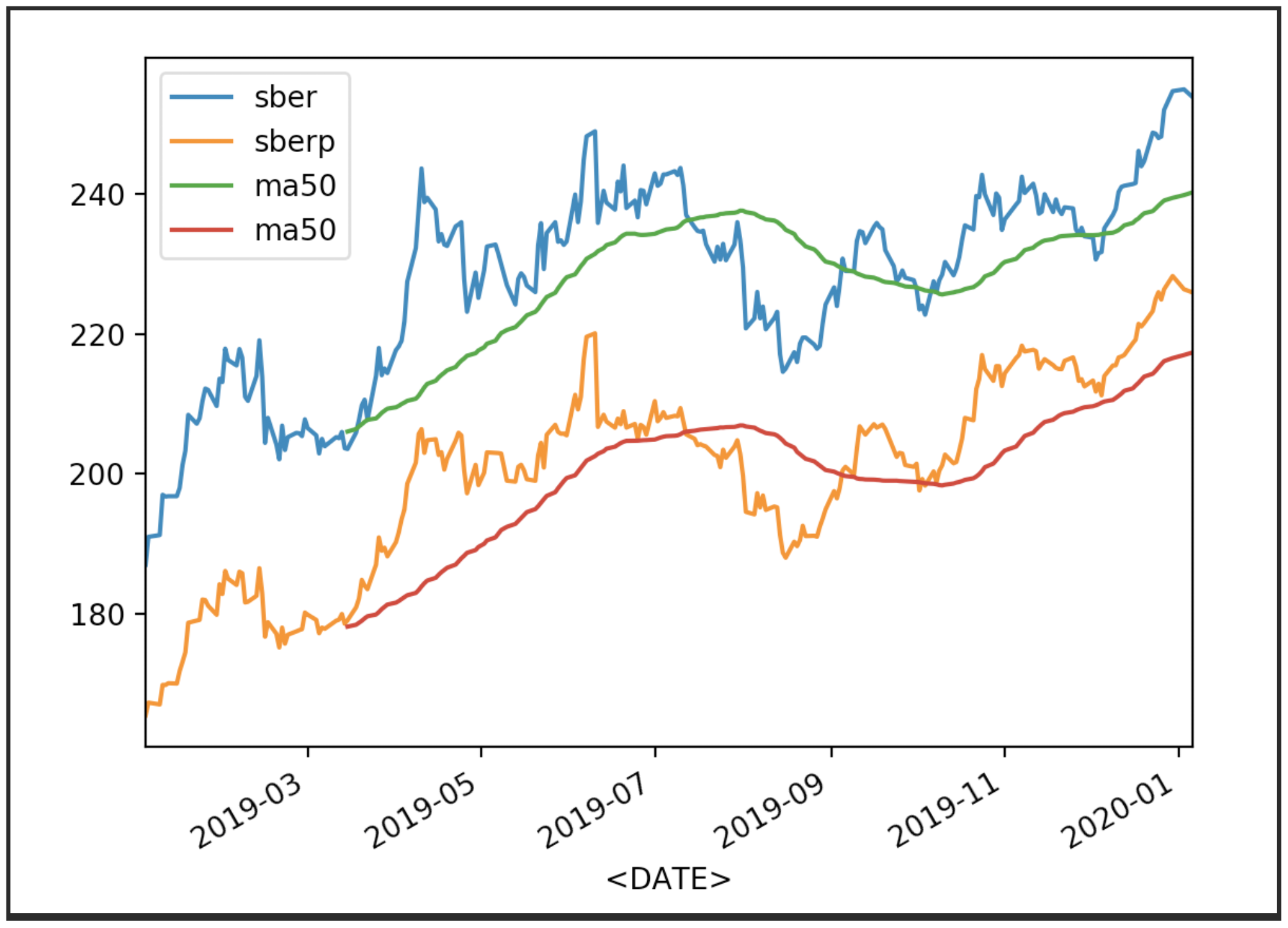
现在显示报价及其平均值（MA 50）：

df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
df['ma50'] = df['<OPEN>'].rolling(50).mean().plot(label='ma50')
df2['ma50'] = df2['<OPEN>'].rolling(50).mean().plot(label='ma50')
plt.legend()
plt.show()



其他平均值也可以显示。

df['<CLOSE>'].plot(label='sber')
df2['<CLOSE>'].plot(label='sberp')
df['ma100'] = df['<OPEN>'].rolling(100).mean().plot(label='ma100')
df2['ma100'] = df2['<OPEN>'].rolling(100).mean().plot(label='ma100')
plt.legend()
plt.show()



现在，我们将显示股票的成交额：
还添加Y轴的名称
和画布的大小

df['total_trade'] = df['<OPEN>']*df['<VOL>']
df2['total_trade'] = df2['<OPEN>']*df2['<VOL>']
df['total_trade'].plot(label='sber',figsize=(16,8))
df2['total_trade'].plot(label='sberp',figsize=(16,8))
plt.legend()
plt.ylabel('Total Traded')
plt.show()



相关分析


现在，让我们仔细看看相关性。矩阵图

将帮助我们解决此问题，创建一个包含两个股票的列的新表并为其命名。

all_sber = pd.concat([df['<OPEN>'],df2['<OPEN>']],axis=1)
all_sber.columns = ['sber_open','sberp_open']
print(all_sber)



现在我们导入必要的时间表

from pandas.plotting import scatter_matrix

并输出：

scatter_matrix(all_sber,figsize=(8,8),alpha=0.2,hist_kwds={'bins':100});
plt.show()

需要澄清的是，我们需要增加透明度（alpha = 0.2）才能看到点的重叠，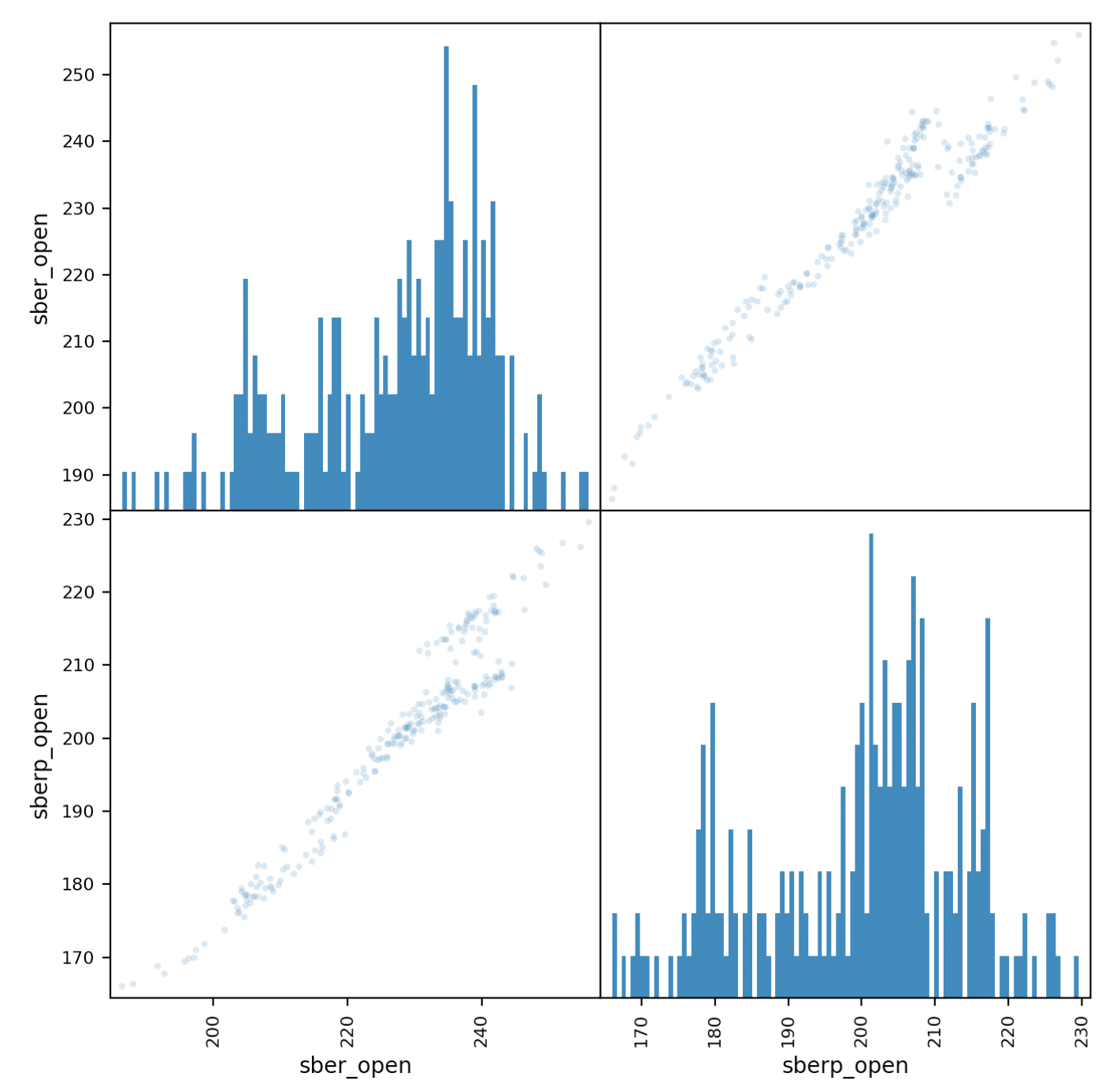



如果点沿对角线“走”了，就会发现相关性。

证券波动率评估


df['returns_pers'].plot(label='sber')
df2['returns_pers'].plot(label='sberp')
plt.legend()
plt.show()



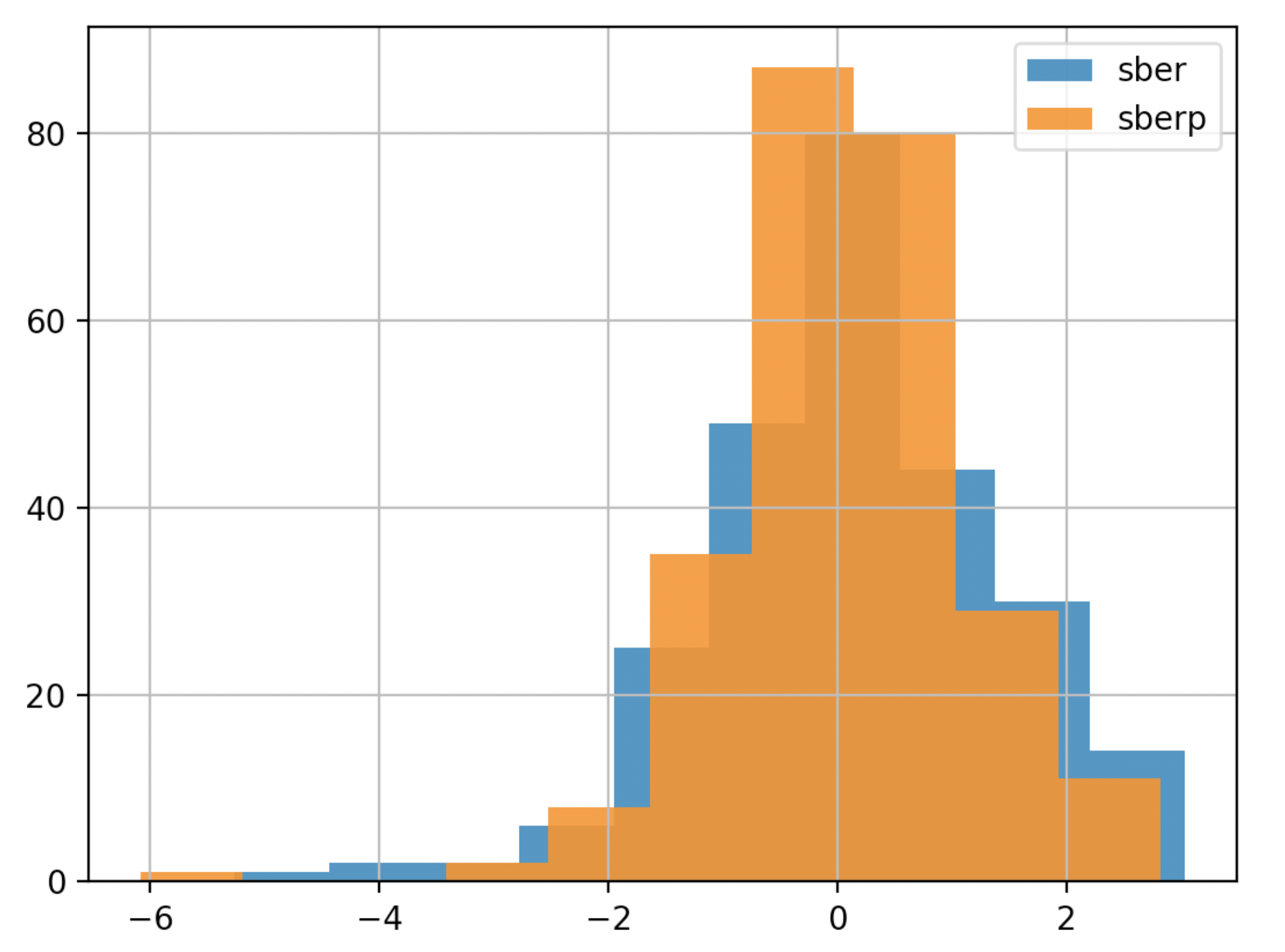
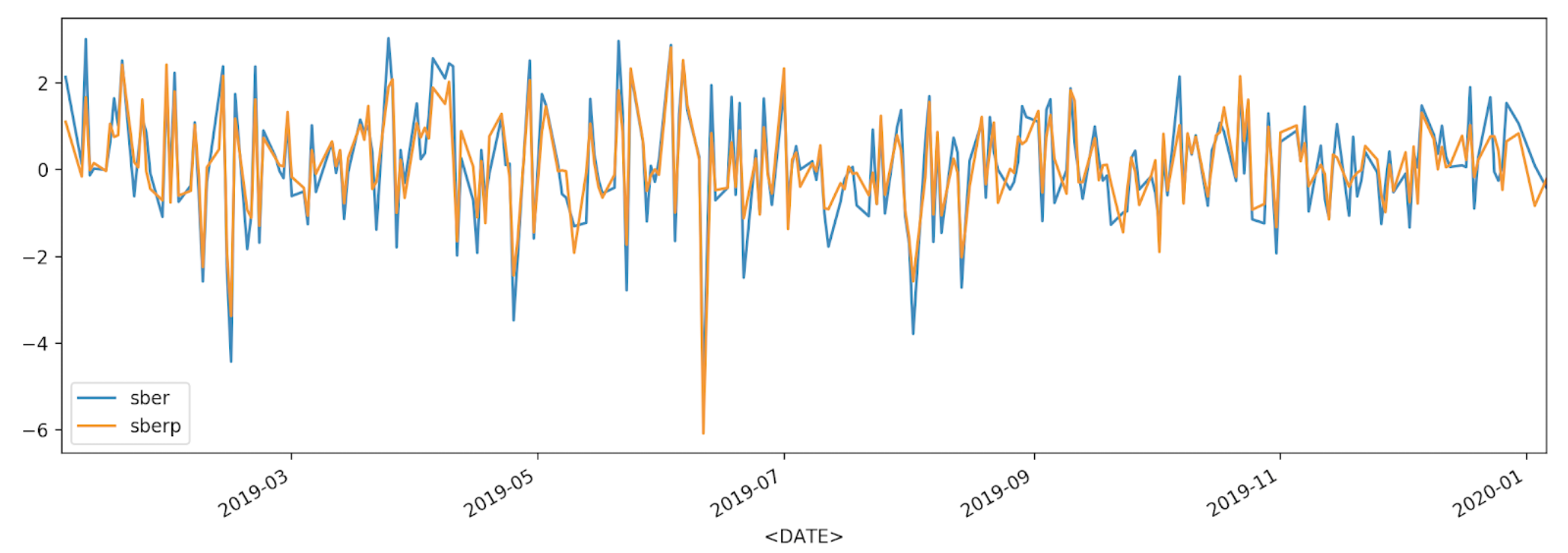为了更好地理解，我们将在另一张图表上显示波动率-直方图

df['returns_pers'].hist(bins=100,label='sber',alpha=0.5)
df2['returns_pers'].hist(bins=100,label='sberp',alpha=0.5)
plt.legend()
plt.show()



为了更快地得出结论，您可以简化时间表（我们将使图表更详细，更不透明）：

df['returns_pers'].hist(bins=10,label='sber',alpha=0.9)
df2['returns_pers'].hist(bins=10,label='sberp',alpha=0.9)
plt.legend()
plt.show()



累计收入分析


现在输出股份价值的百分比变化。

为此，请输入累积收入列。

df['Cumulative Return'] = (1+ df['returns']).cumprod()
df2['Cumulative Return'] = (1+ df2['returns']).cumprod()
print(df)
print(df2)

df['Cumulative Return'].plot(label='sber')
df2['Cumulative Return'].plot(label='sberp')
plt.legend()
plt.show()



在图表上，我们可以看到一只股票相对于另一只股票被低估或重估的时间间隔。在当前情况下（请注意黄蜂），这将有助于我们在Sberbank的资本总额下降时选择要平均的股票。

More articles:


All Articles