哈Ha！我们提醒您，我们早些时候宣布了“ 没有多余单词的机器学习 ”这本书，现在已经开始销售。尽管对于MO的初学者来说，这本书确实可以变成台式机，但其中的某些主题仍然没有被触及。因此，我们为所有感兴趣的人提供了Simon Kerstens撰写的有关MCMC算法本质的文章的翻译，以及该算法在Python中的实现。马尔可夫链的蒙特卡洛方法（MCMC）是一类功能强大的方法，用于从仅直到某个（未知）归一化常数已知的概率分布中进行采样。但是，在研究MCMC之前，让我们讨论为什么您可能甚至需要进行这样的选择。答案是：您可能对样本本身感兴趣（例如，使用贝叶斯推导方法确定未知参数），或对函数相对于概率分布的期望值进行近似估计（例如，根据统计物理学中的状态分布来计算热力学量）。有时我们只对概率分布模式感兴趣。在这种情况下，我们通过数值优化的方法获得它，因此没有必要进行完全选择。结果表明，除了最原始的概率分布之外，从任何概率分布中采样都是一项艰巨的任务。逆变换方法是一种用于从概率分布中采样的基本技术，但是，这需要使用累积分布函数，而要使用该函数，则需要知道通常不知道的归一化常数。原则上，可以通过数值积分获得归一化常数，但是随着尺寸数量的增加，该方法很快变得不可行。偏差采样它不需要规范化的分布，但是为了有效地实现它，需要花很多时间来了解我们感兴趣的分布。此外，此方法还存在严重的尺寸诅咒问题-这意味着其有效性随着变量数量的增加而迅速降低。这就是为什么您需要智能地组织来自分销的代表性样品的接收-无需知道标准化常数。MCMC算法是专门为此设计的一类方法。他们回到大都市和其他城市的标志性文章 ; Metropolis开发了第一个以他命名的MCMC算法并用于计算二维硬球系统的平衡状态。实际上，研究人员正在寻找一种通用的方法，该方法可以让我们计算统计物理学中发现的期望值。本文将介绍MCMC采样的基础知识。马可夫链现在，我们了解了为什么需要采样，让我们继续进入MCMC的核心：马尔可夫链。什么是马尔可夫链？无需赘述技术细节，我们可以说马尔可夫链是某个状态空间中状态的随机序列，其中选择某个状态的概率仅取决于链的当前状态，而不取决于其过去的历史：该链没有内存。在某些条件下，马尔可夫链具有唯一的稳态分布，会收敛到该状态，从而克服了一定数量的状态。在马尔可夫链中有如此多的状态之后，获得不变分布。为了从分布中采样，
MCMC算法创建并模拟了一个马尔可夫链，其静态分布为;这意味着在最初的“种子”阶段之后，这种马尔可夫链的状态将根据原理进行分配。因此，我们仅需保存状态即可从中获取样本。出于教育目的，让我们考虑离散的状态空间和离散的“时间”。表征马尔可夫链的密钥数量是过渡操作者
指示的存在的状态下的概率
在时间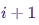
，只要该链处于这样的状态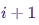在时间i。现在只是为了好玩（并作为演示），让我们快速编织具有唯一固定分布的Markov链。让我们从图表的一些导入和设置开始：%matplotlib notebook
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 6]
np.random.seed(42)
马尔可夫链将绕过由三种天气情况形成的离散状态空间：state_space = ("sunny", "cloudy", "rainy")
在离散状态空间中，过渡算子只是一个矩阵。在我们的情况下，列和行对应于晴天，多云和多雨的天气。让我们为所有过渡的概率选择相对合理的值：transition_matrix = np.array(((0.6, 0.3, 0.1),
(0.3, 0.4, 0.3),
(0.2, 0.3, 0.5)))
行指示电路当前可能位于的状态，而列指示电路可以进入的状态。如果我们在一个小时内走完马尔可夫链的“时间”步骤，那么，假设现在天气晴朗，那么下一个小时就有60％的机会继续晴天。接下来的一个小时还有30％的可能性会出现多云天气，晴天之后会立即下雨的可能性是10％。这也意味着每行中的值加起来为1。让我们稍微推动一下我们的马尔可夫链：n_steps = 20000
states = [0]
for i in range(n_steps):
states.append(np.random.choice((0, 1, 2), p=transition_matrix[states[-1]]))
states = np.array(states)
我们可以观察马尔可夫链如何收敛到平稳分布，并根据链长来计算每个状态的经验概率：def despine(ax, spines=('top', 'left', 'right')):
for spine in spines:
ax.spines[spine].set_visible(False)
fig, ax = plt.subplots()
width = 1000
offsets = range(1, n_steps, 5)
for i, label in enumerate(state_space):
ax.plot(offsets, [np.sum(states[:offset] == i) / offset
for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
despine(ax, ('top', 'right'))
plt.show()
所有MCMC的荣誉：都市圈算法当然，所有这些都非常有趣，但要回到任意概率分布的采样过程
。它可以是离散的（在这种情况下我们将继续讨论过渡矩阵）
，也可以是连续的（在这种情况下它将是过渡核心）。在下文中，我们将讨论连续分布，但是我们在这里考虑的所有概念也适用于离散情况。如果我们可以这样设计过渡核心，使得已经从中推导出下一个状态，那么这将是有限的，因为我们的马尔可夫链...将直接从中采样。不幸的是，要实现这一目标，我们需要能够从我们无法做的-否则您不会阅读，对不对？解决方法是将过渡核心
分为两个部分：提议步骤和接受/拒绝步骤。辅助分布出现在采样步骤
从中选择链的可能的下一状态。我们不仅可以从该分布中进行选择，而且可以随意选择分布本身。但是，在设计时，应该努力实现一种配置，在这种配置中，将从这种分布中获取的样本与当前状态的关联性降到最低，同时有很好的机会经历接收阶段。上述接收/丢弃步骤是过渡核心的第二部分；在此阶段，将从中选择的试用状态中包含的错误进行更正
。在此，计算成功接收的概率，
并以概率作为链中的下一个状态进行采样。从中获取下一个状态然后执行以下操作：首先，从中获取试用状态。然后将其作为具有概率的下一个状态，或以概率丢弃
，在后一种情况下，将当前状态复制并用作下一个状态。因此，
对于马尔可夫链，我们具有充分的条件，因为其稳态分布如下：过渡核必须提交详细的平衡，或者如物理文献中所述，微观可逆性：
。这意味着处于状态
并从那里移动到
必须等于逆过程的概率，即能够进入某种状态。大多数MCMC算法的过渡内核都满足此条件。为了使两部分过渡核心服从详细的均衡，必须正确选择
，即确保它允许您校正从/到或的概率流中的任何不对称性。都市黑斯廷斯算法使用受理标准都市报：
。魔术开始了：我们只知道一个常数，但这并不重要，因为这个未知常数会使...的表达式无效！正是paccpacc属性确保了基于Metropolis-Hastings算法的算法在非规范分布上的运行。通常使用对称辅助分布c 
，在这种情况下，Metropolis-Hastings算法简化为1953年开发的原始（较不通用）Metropolis算法。在原始算法中
。在这种情况下，Metropolis-Hastings的完整过渡核心可以写为
。我们在PYTHON实施了都市警戒算法好了，既然我们已经弄清楚了Metropolis-Hastings算法是如何工作的，那么让我们继续执行它。首先，我们确定要从中进行选择的分布的对数概率-没有归一化常数；假定我们不认识他们。接下来，我们使用标准正态分布：def log_prob(x):
return -0.5 * np.sum(x ** 2)
接下来，我们选择对称辅助分布。通常，如果您包含要从中进行选择的已知分布信息，则可以改善Metropolis-Hastings算法的性能。一种简化的方法是这样的：我们获取当前状态x并从中选择一个样本，即设置一个特定的步长，Δ并从当前状态向左或向右移动不超过
：def proposal(x, stepsize):
return np.random.uniform(low=x - 0.5 * stepsize,
high=x + 0.5 * stepsize,
size=x.shape)
最后，我们计算提案被接受的可能性：def p_acc_MH(x_new, x_old, log_prob):
return min(1, np.exp(log_prob(x_new) - log_prob(x_old)))
现在，我们将所有这些放到Metropolis-Hastings算法的采样阶段的真正简短实现中：def sample_MH(x_old, log_prob, stepsize):
x_new = proposal(x_old, stepsize)
accept = np.random.random() < p_acc(x_new, x_old, log_prob)
if accept:
return accept, x_new
else:
return accept, x_old
除了在马尔科夫链中的下一个状态，x_new或者x_old，我们也返回有关MCMC步是否被采纳的信息。这将使我们能够跟踪样品收集的动态。在此实现的最后，我们编写了一个函数，该函数将迭代调用sample_MH并因此构建马尔可夫链：def build_MH_chain(init, stepsize, n_total, log_prob):
n_accepted = 0
chain = [init]
for _ in range(n_total):
accept, state = sample_MH(chain[-1], log_prob, stepsize)
chain.append(state)
n_accepted += accept
acceptance_rate = n_accepted / float(n_total)
return chain, acceptance_rate
测试我们的都市行为算法并研究其行为也许，现在您迫不及待想要看到所有这些都在起作用。我们将这样做，我们将对参数stepsize和做出一些明智的决定n_total：chain, acceptance_rate = build_MH_chain(np.array([2.0]), 3.0, 10000, log_prob)
chain = [state for state, in chain]
print("Acceptance rate: {:.3f}".format(acceptance_rate))
last_states = ", ".join("{:.5f}".format(state)
for state in chain[-10:])
print("Last ten states of chain: " + last_states)
Acceptance rate: 0.722
Last ten states of chain: -0.84962, -0.84962, -0.84962, -0.08692, 0.92728, -0.46215, 0.08655, -0.33841, -0.33841, -0.33841
事情很好。那么，行得通吗？在大约71％的案例中，我们成功地进行了抽样，并且拥有一系列的州。链还没有收敛到其静态分布的前几个州应该被丢弃。让我们检查一下我们选择的条件是否实际上具有正态分布：def plot_samples(chain, log_prob, ax, orientation='vertical', normalize=True,
xlims=(-5, 5), legend=True):
from scipy.integrate import quad
ax.hist(chain, bins=50, density=True, label="MCMC samples",
orientation=orientation)
if normalize:
Z, _ = quad(lambda x: np.exp(log_prob(x)), -np.inf, np.inf)
else:
Z = 1.0
xses = np.linspace(xlims[0], xlims[1], 1000)
yses = [np.exp(log_prob(x)) / Z for x in xses]
if orientation == 'horizontal':
(yses, xses) = (xses, yses)
ax.plot(xses, yses, label="true distribution")
if legend:
ax.legend(frameon=False)
fig, ax = plt.subplots()
plot_samples(chain[500:], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
看起来不错！参数stepsize和n_total呢？我们首先讨论步长：它决定了可以从电路的当前状态中去除试验状态的距离。因此，这是一个辅助分布参数q，用于控制马尔可夫链所采取的随机步长。如果步长太大，则试验状态通常会落在分布的尾部，那里的概率值很低。 Metropolis-Hastings采样机制放弃了这些步骤中的大多数步骤，从而降低了接收速率，并且收敛速度大大降低。你自己看：def sample_and_display(init_state, stepsize, n_total, n_burnin, log_prob):
chain, acceptance_rate = build_MH_chain(init_state, stepsize, n_total, log_prob)
print("Acceptance rate: {:.3f}".format(acceptance_rate))
fig, ax = plt.subplots()
plot_samples([state for state, in chain[n_burnin:]], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
sample_and_display(np.array([2.0]), 30, 10000, 500, log_prob)
Acceptance rate: 0.116
不是很酷吧？现在看来，最好设置一个很小的步长。事实证明，这也不是明智的决定，因为马尔可夫链将非常缓慢地研究概率分布，因此也不会像选择好的步长那样快收敛：sample_and_display(np.array([2.0]), 0.1, 10000, 500, log_prob)
Acceptance rate: 0.992
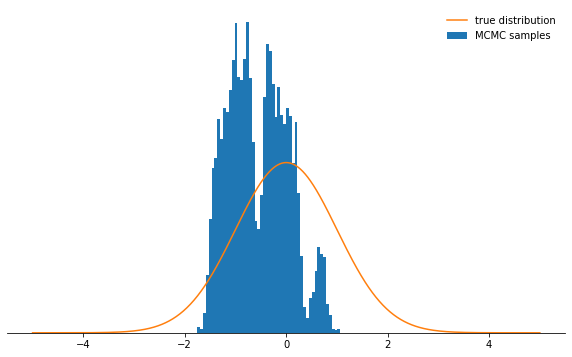无论您如何选择步长参数，马尔可夫链最终都会收敛到平稳分布。但这可能会花费很多时间。我们将模拟马尔可夫链的时间由参数n_total决定-它仅确定我们最终将拥有多少个马尔可夫链状态（并因此选择了样本）。如果链收敛缓慢，则需要增加n_total该链，以使马尔可夫链有时间“忘记”初始状态。因此，我们将使步长很小，并通过增加参数来增加样本数量n_total：sample_and_display(np.array([2.0]), 0.1, 500000, 25000, log_prob)
Acceptance rate: 0.990
Meeeedenly我们正朝着目标......结论考虑到上述所有的，我希望现在你已经直观地掌握都市-黑斯廷斯算法，其参数的本质，明白这是为什么从非标准概率分布的选择，你可以在实践中遇到的一个非常有用的工具。我强烈建议您尝试使用此处给出的代码。-这样您就可以习惯各种情况下的算法行为并更深入地了解它。尝试非对称辅助分配！如果您没有正确配置接受标准，将会发生什么？如果您尝试从双峰分布中采样，会发生什么？您能提出一种自动调整步长的方法吗？这里有什么陷阱？自己回答这些问题！