哈Ha！我向您介绍华盛顿大学塔科马分校Erik R. Tou 撰写的文章“数学起源：逻辑思想”的译文。

译者的话：

在美国数学协会杂志上发表了有关数学起源以及特别是符号的一系列文章。在我看来，到目前为止发表的五篇文章中的最后两篇对我来说似乎是最有趣的，所以我发表了其中第一篇的译本-“数学起源：逻辑思想”。

数学专业的学生一旦掌握了数学分析和统计学的知识，就会出现数学的逻辑上层结构出现的时刻。这可能以明显的问题或至少对所谓的数学真理的可靠性感到某种不适的形式表现出来。我们如何确定经典结果的准确性-例如拉格朗日定理或中心极限定理？在这一点上，许多数学本科课程开始包括数学逻辑和思想课程。

根据作者的经验[ Eric Tou-大约 反式]，这通常包括观念顺序的改变，从解决问题中常见的“发现顺序”到“逻辑顺序”，后者构成了数学证明的基础。很快变得很明显，为了阐明所考虑的数学陈述和逻辑关系，必须使用新的术语和符号。诸如合取与析取，隐含与等价，普遍性和存在性之类的概念必须仔细分开。如今，逻辑理论及其固有符号已被不可分割地考虑：一个逻辑并不独立存在。然而，情况并非总是如此！在本文中，我们将探讨一些较早尝试以系统的方式组织逻辑理论的方法，以及有关符号的一些决定。走着瞧，17世纪和18世纪的作者基本上对描述逻辑思维方式感兴趣，通常是通过与已经存在的数学或哲学概念进行类比。在本系列的下一篇文章中，我们将继续在19世纪和20世纪进行叙述，以探索提议用来描述逻辑的许多符号系统。

约翰·拉恩（Johann Rahn）的早期角色

对于许多学生来说，部分逻辑符号出现在数学学习的开始，通常是缩写或缩写，以简化思维过程。一个很好的例子是使用符号“$$$\therefore$

图。1。约翰·拉恩（Johann Rahn）在“ Teutsche代数”中的代数证据$$$\therefore$ 对于“因此”和 $$$\ast$. Google Books , .

«$$$\therefore$» , ergo. , : $$$18\sqrt{dd-cc} : (c+d)\sqrt{dd-cc} :: 18 : c+d$2 3 $$$(18c + 18d)\sqrt{dd - cc} = (18c + 18d)\sqrt{dd - cc}$. . [Caj, . 212], «$$$\therefore$» «». , .

; 20 , .

. 2. «Teutsche Algebra» . Google Books , .

: $$$D$$$$F$$$$a$$$$b$, $$$D$$$$F$, . 3, $$$*$4 , «», 6. $$$a-b$, $$$a+b=D$, . — , , .

- , , , , , . ( — , ). , , , . , , : , . , . « », :

1. , ;
2. , ;
3. , .

1666 , «Dissertatio de Arte Combinatoria» (« ») [Lei]. , , (1) -, (2) «» ( ) . , .

, , . , . 1679 , -, , . , «Regulæ ex quibus de bonitate consquentiarum formisque et modis syllogismorum categoryoricorum judicari potest per per numberros» («, , »). « » :

, ,



$$$+20−33+10−3$

$$$+cdh-ef+cd-e$

— , (, $$$+20$$$$-33$) (.. , ) , ($$$+20$ $$$+10$, $$$−33$$$$−3$). , $$$+20$$$$+10$, $$$2$, $$$-33$$$$−3$, $$$11$. , , . [Par, . 26]

. -, , . , , « , , ; ». «» «» «», «». [Tho, . 20], - . -, . . , . , . , « » , .

: «Algebræ Philosophicæ»

1761 , «Algebræ philosophicæ in usum artis inveniendi» (« , ») . , .

3. «Algebræ Philosphicæ» (1761). Archive.org , , .

, . , , $$$\omega$, , , . : , , , , . , (aliquid) (nihil) ($$$\cup$) ($$$\cap$), . , .

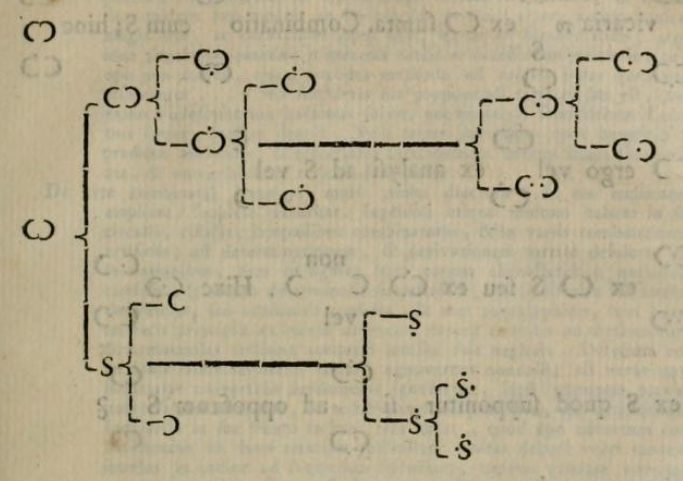
. 4. «Algebræ Philosphicæ» (1761). Archive.org , , London.

— , , ! , :

• (, $$$\omega$), (, $$$\omega$);
• ($$$\omega$), (, ), (, );

, , , , . , (), (). «Algebræ Philosphicæ» 16 , . , ! : «Dissertatio de Arte Combinatoria». , , - «Algebræ Philosphicæ».

Zeichenkunst in der Vernunftlehre

, , 1782 «Sechs Versuche einer Zeichenkunst in der Vernunftlehre» (« »). 5:

. 5. «Sechs Versuche einer Zeichenkunst in der Vernunftlehre» (1782). Google Books , .

, , . , ; , ($$$=$), ($$$+$), ($$$-$), ($$$\times$), ($$$>$) ($$$<$). , . , . ( , ).

, [Lam, . 11]. $$$a$$$$b$, $$$ab$, , , $$$a-ab$$$$a$, $$$b$. , «eigene Merkmale», « », «eigen-» . , $$$b-ab$$$$b$, $$$a$. , $$$a+b-ab-ab$$$$a$$$$b$, , . , , $$$+$, ( ) $$$a$$$$b$. , , $$$a∣b$$$$a$, $$$b$, . $$$a∣b + b∣a + ab + ab = a + b$, , $$$a$$$$b$, $$$a$$$$b$.

…

, , . — — , , , . , , . , , , , , .

, ! 60 , « » ( « ») , . 1847 , , , «» «» « » . , «» , .

. 6. « » (1847). Archive.org , .

, «» « » . « », , . , 19- 20- , « » . , , . !

[Caj] Cajori, Florian. A History of Mathematical Notations, Volume II. Chicago: Open Court Publishing Co., 1928.

[DeM] De Morgan, Augustus. Formal Logic: or, the Calculus of Inference, Necessary and Probable. London: Taylor and Walton, 1847.

[Lam] Lambert, Johann. Sechs Versuche einer Zeichenkunst in der Vernunftlehre. Berlin, 1782.

[Lei] Leibniz, Gottfried Wilhelm, Dissertatio de arte combinatoria. Leipzig, 1666. «Philosophical Papers and Letters» (Leroy E. Loemker, , 2- ) 1969 . « ».

[Par] Parkinson, G. H. R., ed. Leibniz Logical Papers. Oxford: Clarendon Press, 1966. .

[Rah] Rahn，约翰。Teutsche代数。苏黎世：JJ Bodmer，1659年。

[Ric] Richeri，Ludovico。“惯用的代数哲学。” 都灵皇家哲学与数学混合。1（1760-61），46-63。

[Tho]汤姆森，加勒特。在莱布尼兹。康涅狄格州斯坦福德：Thomson Learning，2001年。