对准确性的过分渴望开始产生抵消控制理论和系统理论的作用,因为这导致以下事实:该领域的研究只关注那些问题,而仅关注那些可以精确解决的问题。许多类别的重要问题中,数据,目标和约束过于复杂或定义不充分,以至于无法进行精确的数学分析,仅是因为无法用数学方式解释它们,这些问题仍然存在。扎德
定义和特征
在世界上,很多东西不仅仅被分为白色和黑色,还包括真相和真相。一个人使用许多模糊的概念,以近似,定性的水平评估和比较物理量,物体和系统的状态。因此,我们每个人都可以在不诉诸温度计的情况下估算窗外的温度,并且仅以我们自己的感受和近似估算的标尺(“阴天足以打伞”)为指导。
但是定性评估不具有我们通常数字固有的可加性。也就是说,与自然数(2 + 2)相比,我们无法确定近似估算值(“少量金额” +“少量金额”)的运算结果。我们无法确定,因为定性评估在很大程度上取决于决策者,具体情况和在特定案例中投入的意义。
但是,在世界上,有足够的数量由于某种原因我们无法准确评估:房间的秩序程度,汽车的“声望”,人的美貌,事物的“相似性”……但是我想像平常一样使用它们将用于自动化任务。
这种估计的形式化可以基于模糊集的理论。模糊集的概念在1964年出现,这要感谢起源于阿塞拜疆的美国科学家Lutfi Zadeh。
我们从基本概念开始考虑他的理论。
模糊集(模糊集合) 中的通用集(宇宙)U是一组对
中的通用集(宇宙)U是一组对)%20) ,其中
,其中 ,和
,和
%20) - 的隶属函数一个模糊集合
- 的隶属函数一个模糊集合 ,
,![\ mu_A(u):U→[0; 1]](https://tex.s2cms.ru/svg/%20%5Cmu_A%20(u)%3AU%20%E2%86%92%5B0%3B1%5D%20) 。模糊集也可以写成
。模糊集也可以写成%7D(%5Cmu_A%20(u)%20%2F%20u)%20%3D%20%5Cleft%5C%7B%20%20(%5Cmu_A(u)%20%2F%20u)%20%5Cright%5C%7D%20%20) 。
。
U %20) ( ) u (-)
( ) u (-)  . , . - .
. , . - .
%20) ( . ), – . – U
( . ), – . – U  . , , .
. , , .
, %20%3D%20%5Cbegin%7Bcases%7D1%20%26%20u%20%5Csubseteq%20A%20%5C%5C0%20%26%20u%20%5Cnsubseteq%20A%20%5Cend%7Bcases%7D%20) , .
, .
, %20) :
:
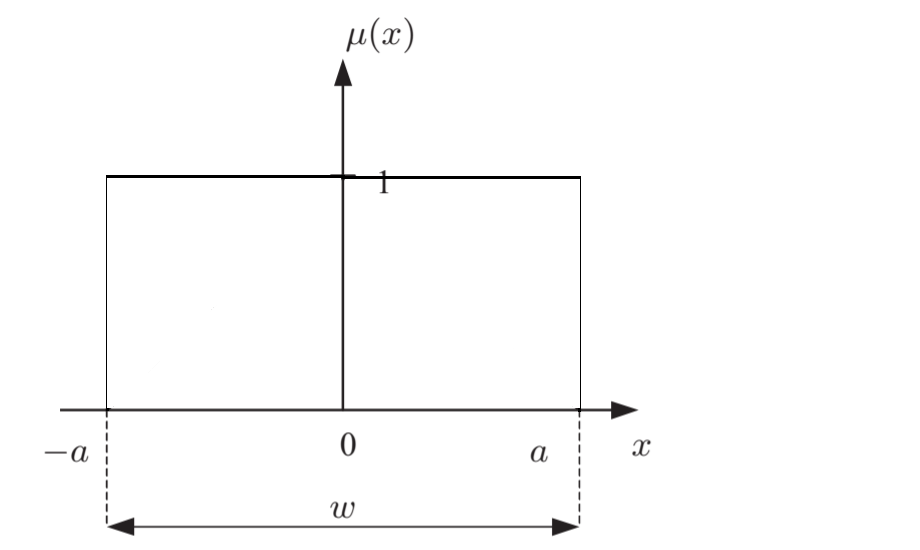
-a≤x≤a.
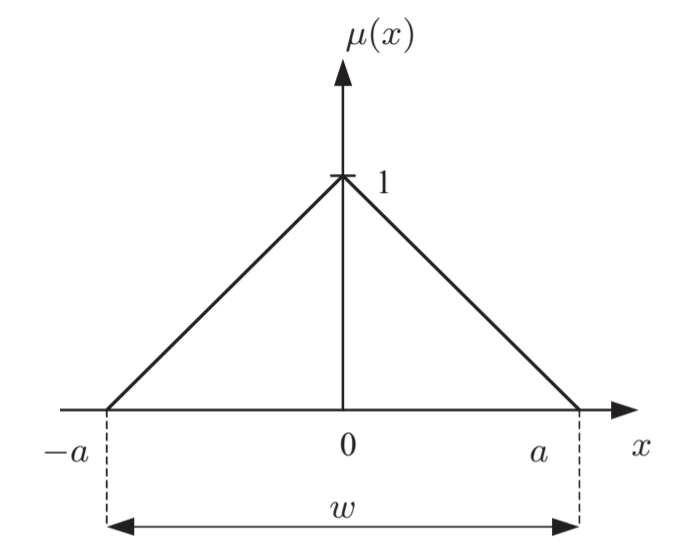
“ ”.
%3D%20%5Cfrac%7B(a-%7Cx%7C)%7D%7Ba%7D%2C%20%20-a%20%5Cleq%20x%20%5Cleq%20a%20)
 .
.
.
– , 1. 0.
, %20) 0.5, . -a/2 a/2.
0.5, . -a/2 a/2.
)%2Cu%20%5Csubseteq%20U%20) .
.
, 1, . – .
, , 0, .
, 1 .
2 %20)
%3E0%2C%20%20x%20%5Csubseteq%20X%20%5Cright%5C%7D%20) –
–  .
. 
 .
.
, x, %3D0%20) ; –
; – %7D%3D0%20) .
.
, , . :
- , ;
- , ;
- , , .
:  — U,
— U,  . , .
. , .
 ,
, %3D%20%5Cmu_B(x)%20) .
.
 ,
, %20%5Cleq%20%0A%20%5Cmu_B%20(x)%20) x.
x.
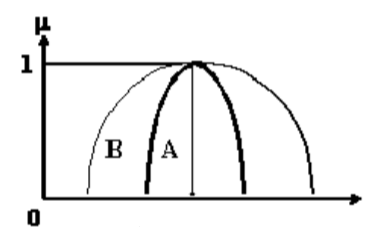
 ,
, %20%3D%20max%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cvee%20%5Cmu_B%20(x)%20) . (t– s–)
. (t– s–)
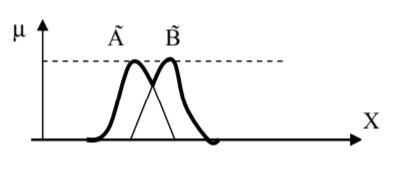
 ,
, %20%3D%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cwedge%20%5Cmu_B%20(x)%20) . (t-)
. (t-)
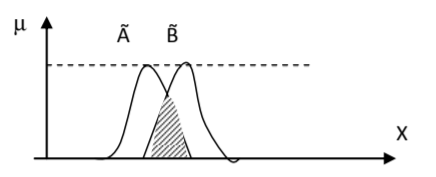
:
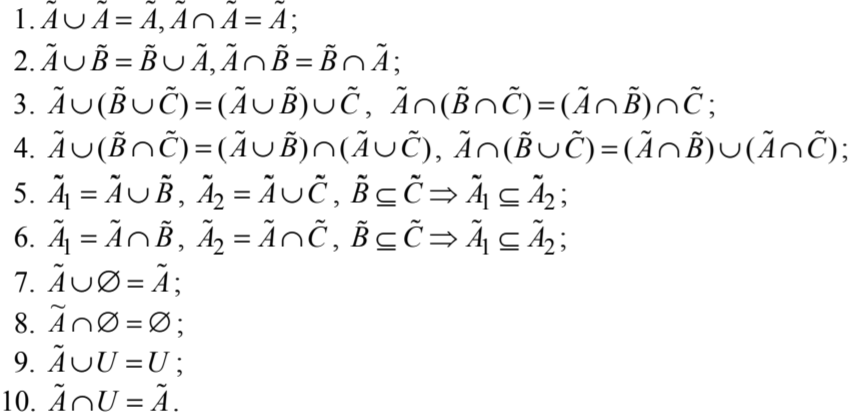
. , , . , min max .
 ,
, %20%3D%20%5Cmu_A(x)%20-%20%5Cmu_%7BA%20%5Ccap%20B%7D(x)%20%3D%20%5Cmu_A(x)%20-%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20%3D%20max(0%3B%20%5Cmu_A(x)%20-%20%5Cmu_B(x))%20) .
.

 . ,
. , %20%3D%201-%20%5Cmu_%7B%5Coverline%7BA%7D%7D(x)%20) .
.
. , , , (,  ). :
). :
α- . α-  ,
, %20%5Cgeq%20%5Calpha%20) .
.
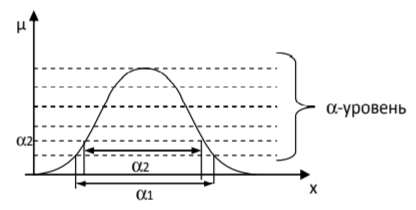
.  , M — .
, M — .
 ,
, %3D%20%5Cmu_A%5E%7B%5Cbeta%7D(x)%20) . :
. :
- β = 2 ( CON(A) ). , . , “ ” ;
- β = 0.5 ( DIL(A) ). , . “ ”.
.
%20%3D%20%5Cmu_A(x)%20*%20%5Cmu_B%20(x)%20) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cvee%200%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%201%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%201%5C%5C0%20%26%20%5Cend%7Bcases%7D%20) .
.
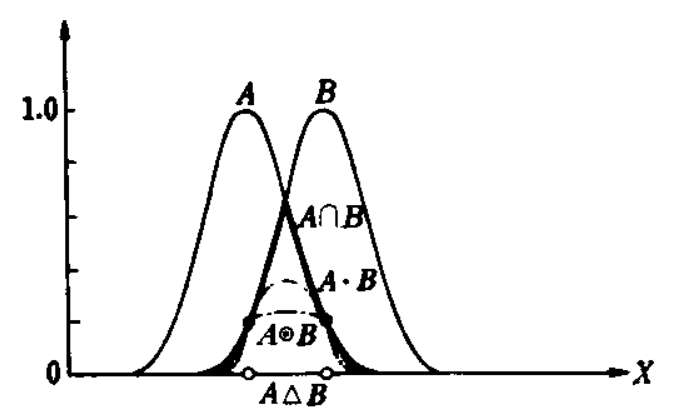
%20%3D%20%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%20%5Cmu_A(x)*%5Cmu_B(x)) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cwedge%201%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%200%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%200%5C%5C1%20%26%20%5Cend%7Bcases%7D%20) .
.
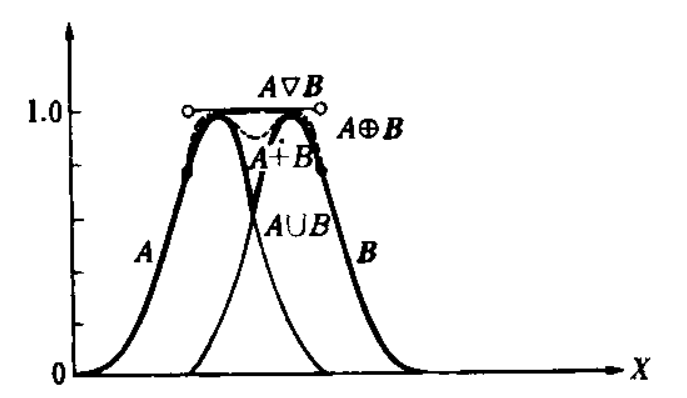
- – A B λ (1 — λ) ( A B). %20%3D%20%5Clambda%20*%20%5Cmu_A(x)%20%2B%20(1%20-%20%5Clambda)%20*%20%5Cmu_B(x)%20) .
.
, λ- :

?
, , . . , ( , ). 2 – .
, . , , , . : , .
, , . , .
, , , , , :
- 0 <= μ(x) <= 1;
- ( );
- 该功能和一组定义的功能必须自然区分由相邻集合代表的概念;
- 没有关联的通用集(不应考虑限制)上不应有任何差距;
- 对于相邻集合,其中一个的最大值必须与另一个的最小值重合,并且它们的图的交点必须与过渡点相对应。
- 以及其他一些特定于任务的任务。
尽管在某些特殊情况下,必须根据上下文确定功能。这些功能的构造是一个单独且相当复杂的主题。
今天就这些。