本文的翻译是专门为Python开发人员课程的学生准备的。
当您使用C之类的低级语言编写代码时，您担心会为整数选择正确的数据类型和限定符，在每一步中，您都需要分析简单地使用它int是否足够或者是否需要添加long或什至long double。但是，在用Python编写代码时，您无需担心这些“次要”的事情，因为Python可以处理integer任何大小类型的数字。在C语言中，如果尝试使用内置函数计算2 20000powl，则将获得输出inf。
int main(void) {
printf("%Lf\n", powl(2, 20000));
return 0;
}
$ ./a.out
inf
但是在Python中，使此过程比以往更容易：>>> 2 ** 20000
39802768403379665923543072061912024537047727804924259387134 ...
...
... 6021 digits long ...
...
6309376
Python确实必须做的非常漂亮，今天，我们将了解它如何处理任意大小的整数！介绍和定义
Integer 在Python中，这是一个C结构，定义如下：struct _longobject {
PyObject_VAR_HEAD
digit ob_digit[1];
};
PyObject_VAR_HEAD是一个宏，它扩展为PyVarObject，其结构如下：typedef struct {
PyObject ob_base;
Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;
其他具有的类型PyObject_VAR_HEAD：- PyBytesObject
- PyTupleObject
- PyListObject
这意味着整数（如元组或列表）具有可变长度，这是了解Python如何支持使用巨型数字的第一步。展开后，该宏_longobject可以视为：struct _longobject {
PyObject ob_base;
Py_ssize_t ob_size; /* Number of items in variable part */
digit ob_digit[1];
};
结构中有PyObject一些元字段用于引用计数（垃圾收集），但是为了讨论这一点，我们需要另外一篇文章。现场上，我们将重点这ob_digit和在一个位ob_size。解密 ob_digit
ob_digit是类型为的单位长度的静态分配的数组digit (typedef uint32_t)。由于这是一个数组，因此它ob_digit主要是指向数字的指针，因此，如有必要，可以使用malloc函数将其增加为任意长度。这样，python可以表示和处理非常长的数字。通常，在C之类的低级语言中，整数的精度限于64位，但是Python支持任意精度的整数。从Python 3开始，所有数字均以表格形式显示bignum，并且仅受可用系统内存的限制。解密 ob_size
ob_size将项目数存储在中ob_digit。Python重写，然后使用该值ob_size确定数组中包含的元素的实际数量，以提高为数组分配内存的效率ob_digit。存储
最简单的整数存储方式是在数组的一个元素中存储一个十进制数字，然后可以根据小学的数学规则执行加减运算。使用这种方法时，将这样保存数字5238：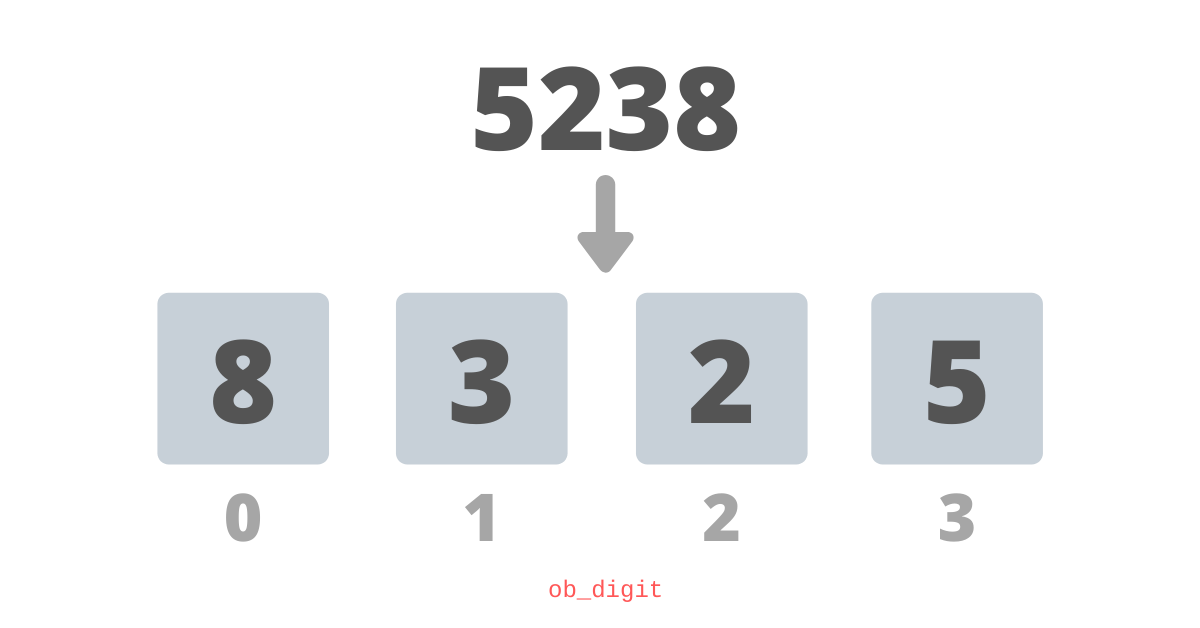
这种方法效率低下，因为我们最多使用32位数字（uint32_t）存储一个十进制数字，实际上，其范围是0到9，并且很容易用4位表示，对于编写像python这样通用的东西，内核开发人员应该更具创造力。那么，我们可以做得更好吗？当然，否则我不会发布这篇文章。让我们仔细看看Python如何存储一个超长整数。Python路径
而不是存储在数组中的每个元素中只有一个十进制数字的ob_digit，Python的转换从数字系统编号为10至数为2的基座中的基座中的系统30和调用每个元件作为数字，其值范围为0〜2 30 - 1在十六进制系统中，基数16〜2 4表示十六进制数字中的每个“数字”范围从0到15。在Python，类似地，一个“数字”为2的基部30，这意味着数量将变化从0到2 30 -十进制1 = 1073741823。这样，Python可以有效地使用几乎所有分配的空间（每位32位），节省资源，并且仍然可以在小学数学级别执行简单的操作，例如加减法。根据平台的不同，Python使用32位无符号整数数组或15位数字的16位无符号整数数组。要执行稍后将要讨论的操作，您只需要一点点。例如：1152921504606846976如已经提到的，用于Python，数字在为2的基础的系统中表示的30，即，是如果转换1152921504606846976成多个系统的2的基底30，将得到1001152921504606846976 = 1 *（2 30）2 + 0 *（2 30）1 + 0 *（2 30）0由于ob_digit最低有效位先被存储，因此它另存为001作为三位。该_longobject值的结构将包含：ob_size 像3ob_digit 像[0，0，1]
我创建了一个演示REPL，将显示的Python如何存储整数内部本身，也指结构成员，如ob_size，ob_refcount等。整数长运算
现在我们对Python如何实现任意精度的整数有了一个清晰的认识，是时候了解如何使用它们执行各种数学运算了。加成
整数以“数字”形式存储，这意味着加法就像在小学一样简单，Python源代码向我们展示了这是实现加法的方式。x_add在文件中具有名称的函数longobject.c将两个数字相加。...
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
z->ob_digit[i] = carry;
...
上面的代码段来自一个函数x_add。如您所见，它会按数字迭代数字并执行数字加法，计算结果并添加连字符。当加法的结果为负数时，它将变得更加有趣。该符号ob_size是一个整数符号，也就是说，如果您有一个负数，那么它将ob_size是一个负号。取ob_size模的值将确定中的位数ob_digit。减法
正如加法一样，减法也一样。x_sub在文件中具有名称的函数longobject.c将从另一个数字中减去一个数字。...
for (i = 0; i < size_b; ++i) {
borrow = a->ob_digit[i] - b->ob_digit[i] - borrow;
z->ob_digit[i] = borrow & PyLong_MASK;
borrow >>= PyLong_SHIFT;
borrow &= 1; /* Keep only one sign bit */
}
for (; i < size_a; ++i) {
borrow = a->ob_digit[i] - borrow;
z->ob_digit[i] = borrow & PyLong_MASK;
borrow >>= PyLong_SHIFT;
borrow &= 1; /* Keep only one sign bit */
}
...
上面的代码段来自一个函数x_sub。在其中，您将看到如何进行数字枚举并执行减法，计算结果并分配转移。确实，它与加法非常相似。乘法
再说一次，乘法将以我们从小学数学课中学到的相同的幼稚方式实现，但是效率不是很高。为了保持效率，Python实现了Karatsuba算法，该算法将两个n位数字乘以O（n log 2 3）个简单步骤。该算法并不简单，其实现超出了本文的范围，但是您可以在函数k_mul 和k_lopsided_mul文件中找到其实现longobject.c。除法及其他业务
所有对整数的操作都在文件中定义longobject.c，它们非常容易找到和跟踪每个工作。注意： 详细了解每个人的工作需要时间，因此请预先储存爆米花。Python 在内存中预分配了少量的整数，范围从-5到256。这种分配发生在初始化期间，并且由于我们不能更改整数（不变性），因此这些预分配的数字是单例的，直接被引用而不是被分配。这意味着每次我们使用/创建一个较小的数字时，Python不会出售它，而是简单地返回对先前分配的数字的引用。可以在宏IS_SMALL_INT和函数get_small_intc中跟踪这种优化longobject.c。因此，Python在计算常用的整数时节省了大量空间和时间。这是Python Internals系列的第二篇文章。第一篇文章是关于我如何更改Python版本以使其实现的big昧。它将帮助您迈出了解Python源代码的第一步，并继续成为Python内核开发人员的道路。如果您想查看更多类似的文章，请订阅我的新闻通讯并直接在收件箱中接收它们。我每个星期五写有关工程学，系统工程学和一些编程的文章。给我发电子邮件@arpit_bhayani。您可以在@ arpitbhayani.me/blog中找到我以前的文章。就这样。在课程中见！