人们满足推荐系统。因式分解

机器学习已经渗透到我们的日常生活中。当有人告诉他们有关智能手机中的神经网络时，不再感到惊讶。推荐系统是该科学领域的一大领域。它们无处不在：当您听音乐，看书，看电视节目或视频时。这种科学的发展发生在YouTube，Spotify和Netfilx等大型公司中。当然，该领域的所有科学成就都在著名的NeurIPS或ICML会议以及不太知名的RecSys上发表。在这个问题上更加敏锐。在本文中，我们将讨论这种科学的发展方式，现在和现在所采用的推荐方法以及所有这些方法背后的数学原理。

我的灵感来自于工作，写这篇文章StatML实验室在Skoltech与推荐系统。

为什么和为谁

为什么这对我们每个人都很重要？看一下下面的列表：

• 影片推荐： YouTube，Netlix，HBO，Amazon Prime，迪士尼+，Hulu，Okko
• 音频建议： Spotify，Yandex.Music，Yandex.Radio，Apple Music
• 产品推荐： Amazon，Avito，LitRes，MyBook
• 搜索建议： Google，Yandex，Bing，Yahoo，Mail
• : Booking, Twitter, Instagram, ., , GitHub

, . , . , , YouTube.

( ), . , , . , ( ). -, . , -, , - . , . , , , , .

, , , , - . , (, , , ..). , .

, . : $$$U$ $$$I$ — . $$$r_{ui}$ $$$u$ $$$i$. , , , , . :

$$

$$\mathcal{D} = \{ (u, i) |\text{ if } \exists r_{ui}, u \in U, i \in I\}$$

$$$f$:

$$

$$f(u, i) = \hat{r}_{ui}\approx r_{ui}$$

, $$$r_{ui}$ 1 5 ( ) : 1 -1 ( / )

3 :

• Content-based (CB)
• Collaborative filtering (CF)
• Hybrid recommendations

. — , . : — , — , . . , : , ..

, . - , .

. , , , .

, , . . , , . .

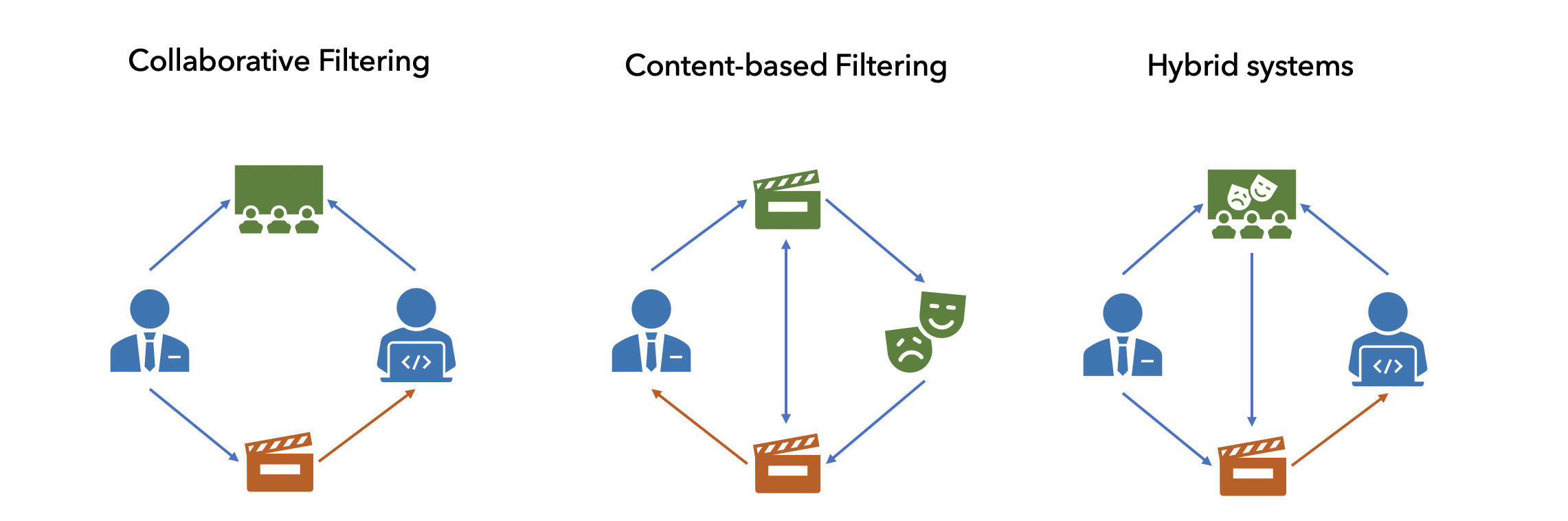
Matrix Factorization

, . : . .

• :
  
  • Singular Value Decomposition (SVD)
  • Singular Value Decomposition with implicit feedback (SVD++)
  • Collaborative Filtering with Temporal Dynamics (TimeSVD++)
  • Weighted Matrix Factorization (WMF or ALS)
  • Sparse Linear Methods (SLIM)
  • Factorization Machines (FM)
• :
  
  • Probabilistic Matrix Factorization (PMF)
  • Bayesian Probabilistic Matrix Factorization (BPMF)
  • Bayesian Factorization Machines (BFM)
  • Gaussian Process Factorization Machines (GPFM)

Singular Value Decomposition (SVD)

— SVD. $$$A$ $$$n \times m$, $$$n = |U|$, $$$m = |I|$. $$$\mathcal{D}$ $$$A_{ui} = r_{ui}$, . SVD , $$$A$ : $$$U,~\Sigma,~V$. $$$k$ , $$$A$.

$$

$$A = U \Sigma V^T, \quad\quad\quad\quad A \approx \hat{A} = \hat{U} \hat{ \Sigma } \hat{V}^T .$$

$$$Q$ $$$P$ . $$$A$ :

$$

$$P = (\hat{U} \hat{ \Sigma })^T, \quad\quad Q = \hat{V}^T, \quad\quad\quad\quad A \approx P^T \cdot Q .$$

:

$$

$$r_{ui} \approx \hat{r}_{ui} = p^T_u q_i .$$

, $$$p_u$ $$$q_i$ — $$$u$ $$$i$ - $$$k$. . . :

$$

$$\Theta = \{ p_u, q_i| u \in U, i \in I\} .$$

c :

$$

$$\sum_{(u, i) \in \mathcal{D}} (r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 = \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p^T_u q_i)^2 + \lambda\sum_{u \in U}\|p_u\|^2 + \lambda\sum_{i \in I}\|q_i\|^2 .$$

, , , , . $$$\hat{r}_{ui}$. (GD) (ALS). Habr- , . , , .

( SVD, SVD$$$_{bias}$). , , . . SVD . (bias):

$$

$$\hat{r}_{ui} =\mu + b_u + b_i + p^T_u q_i ,$$

$$$b_u$ — , $$$b_i$ — , $$$\mu$ — . :

$$

$$\Theta = \{ \mu, b_u, b_i, p_u, q_i| u \in U, i \in I\} .$$

SVD++

Factorization Meets the Neighborhood SVD . (explicit and implicit user feedback). $$$r_{ui}$, . . : $$$R(u)$ — ( ) $$$N(u)$ — ( ).

SVD++ :

$$

$$\hat{r}_{ui} =\mu + b_u + b_i + q^T_i \left( p_u + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) .$$

:

$$

$$\Theta = \{ \mu, b_u, b_i, p_u, q_i, y_i| u \in U, i \in I\} .$$

, $$$N(u)$ $$$R(u)$, .. $$$R(u) \subset N(u)$. (item-item recommendation).

Asymmetric-SVD

SVD++ . . :

$$

$$\hat{r}_{ui} = b_{ui} + q^T_i \left( |R(u)|^{-1/2} \sum_{j \in R(u)} (r_{uj} - b_{uj})x_j + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) ,$$

$$$b_{ui} = \mu + b_u + b_i$

TimeSVD++

TimeSVD++. (MovieLens, Netflix) , . , . Collaborative Filtering with Temporal Dynamics SVD++ :

$$

$$\hat{r}_{ui}(t) =\mu + b_u(t) + b_i(t) + q^T_i \left( p_u(t) + |R(u)|^{-1/2} \sum_{j \in R(u)} y_j \right) .$$

让我们弄清楚时间对每个术语有何影响：
项目偏差：如果您将评分分为几段的时间间隔（工作中建议了30个部分）并添加自己的参数$$$b_{i,\text{Bin}(t)}$ 对于每种产品，根据变量的间隔来选择 $$$t$：

$$

$$b_i(t) = b_i + b_{i, \text{Bin}(t)}$$

用户偏见：在分析Neflix数据时，我们注意到，平均每个用户的排名只有40天。因此，我们将充当商品并添加我们自己的参数$$$b_{u, t}$对于每个用户。我们增加了对时间的线性依赖性-我们引入了另一个术语$$$\alpha_u$ 折旧率：

$$

$$b_i(t) = b_i + \alpha_u \cdot \text{dev}_u(t) + b_{u, t} \quad\quad\quad\quad \text{dev}_u(t) = \text{sign}(t - t_u) \cdot |t - t_u|^{\beta}$$

。
关于如何向用户添加时间依赖项，还有其他选项：
用户嵌入一文中有更详细的描述：我们将为潜在表示的每个组件添加一个类似的技巧。$$$p_u(t) = (p_{u1}(t), \dots, p_{uf}(t))^T$：

$$

$$p_{uk}(t) = p_{uk} + \alpha_{uk} \cdot \text{dev}_u(t) + p_{uk, t}.$$

加权矩阵分解（WMF）和交替最小二乘（ALS）

SVD的主要问题之一是仅使用来自用户的明确响应。这个问题在SVD ++中得到了部分解决。但是还有另一种方式-加权矩阵分解（WMF）。在本文中，他们建议几乎不要更改模型（$$$\hat{r}_{ui} = p^T_u q_i$），并更改学习过程。分配评分$$$r_{ui}$我们不知道的（即夫妻） $$$(u, i) \notin \mathcal{D}$）的值是0。然后每对 $$$(u, i)$ 输入参数 $$$c_{ui}$, $$$r_{ui}$. , . - . YouTube , . , , , . , , , :

$$

$$\sum_{(u, i)} c_{ui}(r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 .$$

: $$$c_{ui} = 1 + \alpha r_{ui}$. : $$$r_{ui}>0$ $$$r_{ui} = 0$. $$$\alpha$ $$$\alpha = 40$ .

, (ALS) . WMF, ALS, .

Fast Alternating Least Squares

ALS , eALS . , . , . .

, $$$c_{ui}$ ALS :

$$

$$c_{ui} = c_i + \alpha r_{ui}, \quad\quad\quad\quad c_i = c_0 \frac{f_i^{\beta}}{\sum_{j \in I} f_j^{\beta}} ,$$

$$$c_0$ $$$\beta$, .

Sparse Linear Methods (SLIM)

Sparse Linear Methods (SLIM) . , SVD . . SLIM :

$$

$$\hat{a}_{ui} = a^T_u w_i \quad\quad\quad\quad \hat{A} = AW$$

$$$W \in \mathbb{R}^{m \times m}$. : $$$W \geq 0$ $$$\text{diag}(W) = 0$. :

$$

$$\frac{1}{2}\|A - AW\|^2_F + \frac{\beta}{2}\|W\|^2_F + \lambda\|W\|_1$$

$$$W$ .

Factorization Machines (FM)

, Factorization Machines (FM). , ( 2- ). :

$$

$$\hat{r}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{i=j+1}^{n} v^T_i v_j ~ x_i x_j, \quad\quad\quad\quad w_0 \in \mathbb{R} ~~~ w \in \mathbb{R}^n ~~~ V \in \mathbb{R}^{n \times k} .$$

(SGD) ( ). , $$$x$ $$$(u, i)$. . , — . — ( ). ( ).

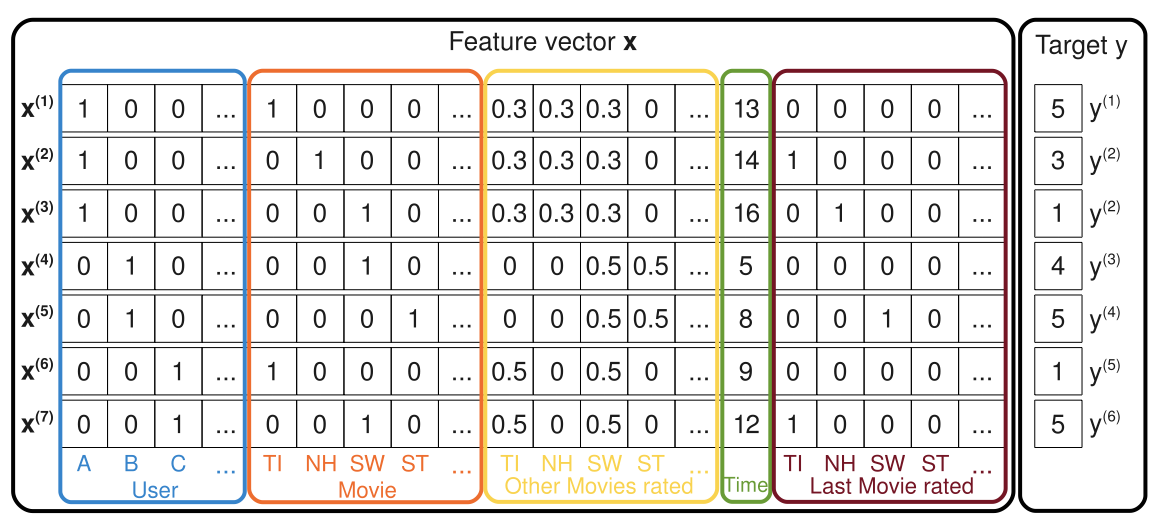
, SVD, SVD++ — FM. SVD , :

$$

$$n = | U \cup I |, \quad\quad\quad x_j = \delta (j = u ~\lor~ j = i) .$$

$$$\delta$ — . .. $$$x$ $$$u$ $$$i$. FM :

$$

$$\hat{r}(x) = w_0 + w_u + w_i + v^T_u v_i .$$

, $$$x$: , . , , , , , , . .

Probabilistic Matrix Factorization (PMF)

, , , .

(PMF), . , SVD: $$$p_u$ $$$q_i$ — . , :

$$

$$p(r | P, Q, \sigma) = \prod_{(u, i) \in \mathcal{D}}\mathcal{N}(r_{ui}| g(p_u^Tq_i), \sigma^2) ,$$

$$$\mathcal{N}$ — , a $$$g(x) = \frac{1}{1 + e^{-x}}$ — (). , , :

$$

$$p(P| \sigma_p) = \prod_{u \in U} p(p_u| 0, \sigma^2_p \mathbf{I}), \quad\quad\quad\quad p(Q| \sigma^2_q) = \prod_{i \in I} p(q_i| 0, \sigma_q^2 \mathbf{I}) .$$

( ) , :

$$

$$\frac{1}{2} \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p_u^T q_i)^2 + \frac{\lambda_p}{2} \sum_{u \in U} \|p_u\|^2 + \frac{\lambda_q}{2} \sum_{i \in I} \|q_i\|^2 ,$$

$$$\lambda_p = \frac{\sigma_p}{\sigma}$ $$$\lambda_q = \frac{\sigma_q}{\sigma}$ — . , SVD , .

Constrained PMF

PMF Constrained PMF. , SVD SVD++. , , $$$p_u$ :

$$

$$p_u + \frac{\sum_{i \in R(u)} y_i}{|R(u)|} ,$$

$$$R(u)$ — , $$$u$.

Bayesian Probabilistic Matrix Factorization (BPMF)

PMF BPMF. PMF , , . :

$$

$$p(P| \mu_p, \Lambda_p) = \prod_{u \in U} p(p_u| \mu_p, \Lambda_p) ,\quad\quad\quad\quad p(Q| \mu_q, \Lambda_q) = \prod_{i \in I} p(q_i| \mu_q, \Lambda_q) .$$

$$$\Theta_p = \{ \mu_p, \Lambda_p \}$ $$$\Theta_q = \{ \mu_q, \Lambda_q \}$ - $$$\Theta_0 = \{ \mu_0, \nu_0, W_0 \}$. , .

Bayesian Factorization Machines (BFM)

, Bayesian, . , $$$\Theta = \{ w_0, w_i, v_i\} .$ , - . : $$$\Theta_H = \{ \lambda_{\theta}, \mu_{\theta} | \theta \in \Theta \}$. .

Gaussian Process Factorization Machines (GPFM)

GPFM . $$$f$ $$$\theta$. $$$\theta_u$ , , :

$$

$$\hat{r}_{ui} = f(q_i, \theta_u)$$

, . , $$$f$ , . , , , .

.

: Bayesian Personalized Ranking (BPR)

BPR , "". , BPR — , , Bayesian Personalized Ranking. . , , $$$i$ $$$j$ $$$u$. $$$(u, i)$ $$$r_{ui}$ $$$(u, i, j)$ $$$i$ $$$j$ ((+) $$$i$ , $$$j$ (-) ). $$$\mathcal{D}_S$. . ( personalized ):

$$

$$p(i <_u j | \Theta) = \sigma(\hat{r}_{uij}(\Theta)) ,$$

$$$\sigma$ — , a $$$\hat{r}_{uij}$ — . (MLE), , :

$$

$$\min_{\Theta} \sum_{(u, i, j) \in \mathcal{D}_S}\ln{\sigma(\hat{r}_{uij})} - \lambda \|\Theta\|^2$$

(SGD):

$$

$$\Theta \leftarrow \Theta + \alpha\left(\frac{e^{-\hat{r}_{uij}}}{1 + e^{-\hat{r}_{uij}}} \cdot \frac{\partial}{\partial \Theta}\hat{r}_{uij} + \lambda \Theta \right)$$

, . , , . SVD:

$$

$$\hat{r}_{uij} = \hat{r}_{ui} - \hat{r}_{uj} \quad\quad\quad\quad \hat{r}_{ui} = p_u^T q_i$$

:

$$

$$\frac{\partial}{\partial \Theta}\hat{r}_{uij} =\begin{cases} (q_{ik} - q_{jk})~~~\text{if } \theta = p_{uk}\\ p_{uk}~~~~~~~~~~~~~~~\text{if } \theta = q_{ik}\\ -p_{uk}~~~~~~~~~~~~\text{if } \theta = q_{jk} \end{cases}$$

BPR ( ) , . , . . , (pairwise approach) (pointwise approach). . , 5 , . , , . — BPR - , . , .

Show must go on

这次我们讨论了推荐系统中的许多分解方法，但是图和神经网络（还有很多有趣的东西）仍然没有被改动。