Dia bom.Apresento a você a tradução do artigo “Algoritmos em gráficos: vamos falar de pesquisa de profundidade (DFS) e pesquisa de profundidade (BFS)” de Try Khov.O que é uma travessia de gráfico?
Em palavras simples, uma travessia de gráfico é uma transição de um de seus vértices para outro em busca das propriedades de conexão desses vértices. Links (linhas que conectam vértices) são chamados de direções, caminhos, faces ou arestas de um gráfico. Os vértices do gráfico também são chamados de nós.Os dois principais algoritmos de passagem de gráfico são Pesquisa Profundidade-Primeira, DFS e Pesquisa Largura-Primeira, BFS.Apesar de os dois algoritmos serem usados para percorrer o gráfico, eles têm algumas diferenças. Vamos começar com o DFS.Pesquisa em profundidade
O DFS segue o conceito de "aprofundar, de cabeça primeiro". A idéia é que nos movamos do pico inicial (ponto, lugar) em uma determinada direção (ao longo de um determinado caminho) até chegarmos ao final do caminho ou destino (pico desejado). Se chegamos ao final do caminho, mas não é um destino, voltamos (ao ponto de caminhos ramificados ou divergentes) e seguimos por um caminho diferente.Vejamos um exemplo. Suponha que tenhamos um gráfico direcionado parecido com o seguinte:
Estamos no ponto "s" e precisamos encontrar o vértice "t". Usando o DFS, investigamos um dos caminhos possíveis, avançamos até o final e, se não encontrarmos t, voltamos e exploramos outro caminho. Aqui está a aparência do processo:
Aqui nos movemos ao longo do caminho (p1) até o pico mais próximo e vemos que esse não é o fim do caminho. Portanto, passamos para o próximo pico.
Chegamos ao final de p1, mas não encontramos t, então voltamos para s e seguimos pelo segundo caminho.
Tendo atingido o topo do caminho “p2” mais próximo do ponto “s”, vemos três direções possíveis para mais movimentos. Como já visitamos o pico que coroa a primeira direção, estamos nos movendo pela segunda.
Chegamos novamente ao final do caminho, mas não encontramos t, então voltamos. Seguimos o terceiro caminho e, finalmente, atingimos o pico desejado "t".
É assim que o DFS funciona. Seguimos um certo caminho até o fim. Se o final do caminho é o pico desejado, estamos prontos. Caso contrário, volte e siga um caminho diferente até explorarmos todas as opções.Seguimos esse algoritmo para todos os vértices visitados.A necessidade de repetição repetida do procedimento indica a necessidade de recursão para implementar o algoritmo.Aqui está o código JavaScript:
function dfs(adj, v, t) {
if(v === t) return true
if(v.visited) return false
v.visited = true
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
let reached = dfs(adj, neighbor, t)
if(reached) return true
}
}
return false
}
Nota: Esse algoritmo DFS especial permite verificar se é possível ir de um lugar para outro. O DFS pode ser usado para vários propósitos. Esses objetivos determinarão a aparência do algoritmo. No entanto, o conceito geral se parece exatamente com isso.Análise DFS
Vamos analisar esse algoritmo. Como contornamos cada "vizinho" de cada nó, ignorando aqueles que visitamos anteriormente, temos um tempo de execução igual a O (V + E).Uma breve explicação do que V + E significa:V é o número total de vértices. E é o número total de faces (arestas).Pode parecer mais apropriado usar V * E, mas vamos pensar no que significa V * E.V * E significa que, com relação a cada vértice, devemos investigar todas as faces do gráfico, independentemente de essas faces pertencerem a um determinado vértice.Por outro lado, V + E significa que para cada vértice avaliamos apenas as arestas adjacentes a ele. Voltando ao exemplo, cada vértice tem um certo número de faces e, na pior das hipóteses, contornamos todos os vértices (O (V)) e examinamos todas as faces (O (E)). Temos vértices V e faces E, então obtemos V + E.Além disso, como usamos recursão para percorrer cada vértice, isso significa que uma pilha é usada (recursão infinita leva a um erro de estouro de pilha). Portanto, a complexidade espacial é O (V).Agora considere o BFS.Pesquisa ampla
O BFS segue o conceito de "expandir amplamente, elevando-se à altura do voo de um pássaro" ("amplie, vista aérea"). Em vez de seguir um determinado caminho até o fim, o BFS envolve avançar um vizinho de cada vez. Isso significa o seguinte:Em vez de seguir o caminho, BFS significa visitar os vizinhos mais próximos de s em uma única ação (etapa), depois visitar os vizinhos dos vizinhos e assim por diante até que t seja detectado.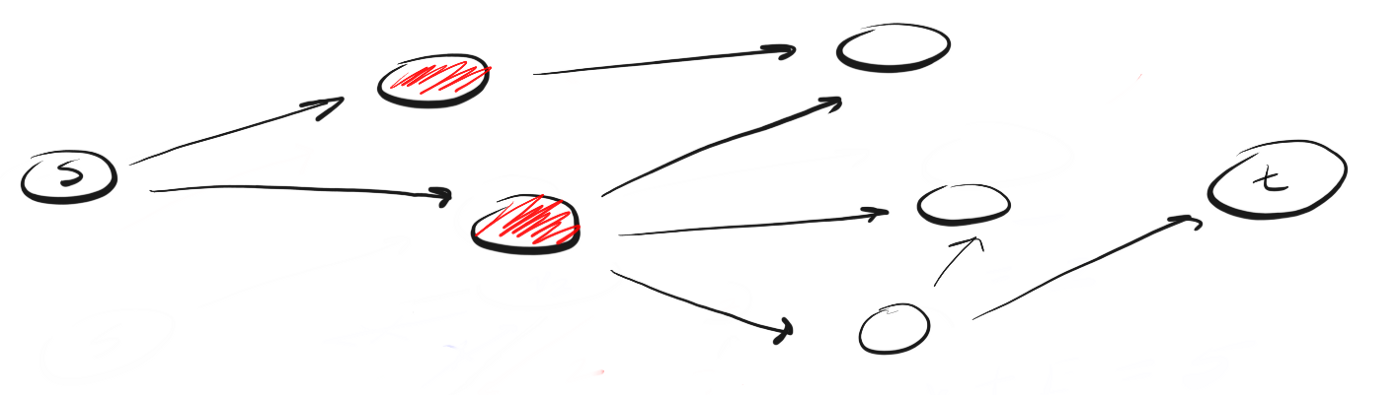
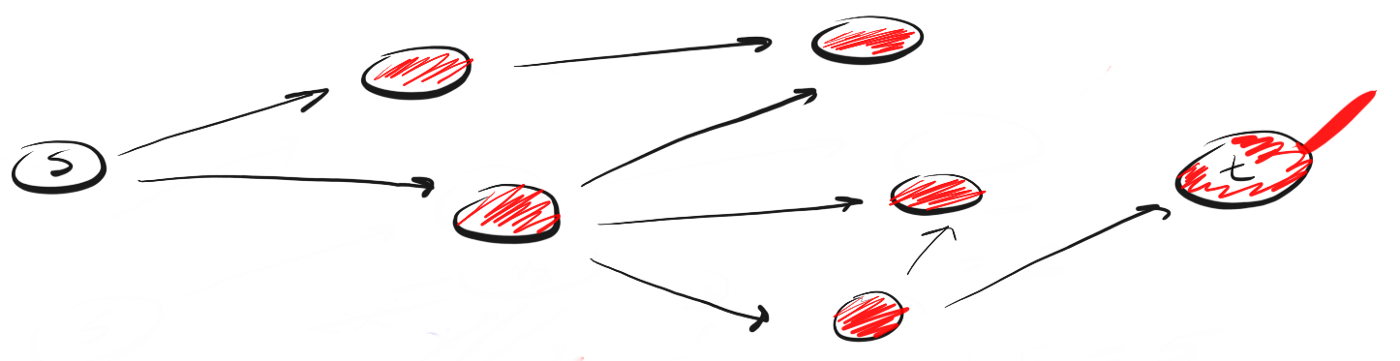Como o DFS é diferente do BFS? Eu gosto de pensar que o DFS segue em frente e o BFS não tem pressa, mas estuda tudo em uma única etapa.Surge então a pergunta: como você sabe quais vizinhos devem ser visitados primeiro?Para fazer isso, podemos usar o conceito de "primeiro a entrar, primeiro a sair" (FIFO), primeiro a entrar, primeiro a sair, na fila. Primeiro, colocamos na fila o pico mais próximo de nós, depois seus vizinhos não visitados, e continuamos esse processo até que a fila esteja vazia ou até encontrarmos o vértice que estamos procurando.Aqui está o código:
function bfs(adj, s, t) {
let queue = []
queue.push(s)
s.visited = true
while(queue.length > 0) {
let v = queue.shift()
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
queue.push(neighbor)
neighbor.visited = true
if(neighbor === t) return true
}
}
}
return false
}
Análise BFS
Pode parecer que o BFS é mais lento. No entanto, se você observar atentamente as visualizações, poderá ver que elas têm o mesmo tempo de execução.Uma fila envolve o processamento de cada vértice antes de chegar a um destino. Isso significa que, na pior das hipóteses, o BFS explora todos os vértices e faces.Apesar do BFS parecer mais lento, na verdade é mais rápido, porque ao trabalhar com gráficos grandes, verifica-se que o DFS passa muito tempo seguindo caminhos que acabam sendo falsos. O BFS é frequentemente usado para encontrar o caminho mais curto entre dois picos.Assim, o tempo de execução do BFS também é O (V + E) e, como usamos uma fila contendo todos os vértices, sua complexidade espacial é O (V).Analogias da vida real
Se você der analogias da vida real, é assim que imagino o trabalho do DFS e BFS.Quando penso no DFS, imagino um rato em um labirinto em busca de comida. Para chegar ao alvo, o mouse é forçado a chegar a um beco sem saída muitas vezes, retornar e se mover de uma maneira diferente, e assim por diante até encontrar uma saída do labirinto ou comida.
Uma versão simplificada é assim:
Por outro lado, quando penso em BFS, imagino círculos na água. A queda de uma pedra na água leva à propagação de distúrbios (círculos) em todas as direções a partir do centro.
Uma versão simplificada é assim:
achados
- Pesquisas de profundidade e largura são usadas para percorrer o gráfico.
- O DFS se move pelas bordas para frente e para trás, e o BFS se espalha pelos vizinhos em busca de um destino.
- O DFS usa a pilha e o BFS a fila.
- O tempo de execução de ambos é O (V + E) e a complexidade espacial é O (V).
- Esses algoritmos têm uma filosofia diferente, mas são igualmente importantes para trabalhar com gráficos.
Nota Por.: Eu não sou especialista em algoritmos e estruturas de dados; portanto, se forem encontrados erros, imprecisões ou formulações incorretas, escreva em uma carta pessoal para correção e esclarecimento. Eu serei grato.Obrigado pela atenção.