O guilloché é um padrão característico do papel-moeda e de outros títulos. Uma história detalhada sobre eles com uma digressão na história pode ser encontrada no artigo anterior . Um algoritmo de desenho que constrói guilhotinas por pontos também foi dado lá.Bastante inútil, deve-se notar se os desenharmos não apenas por diversão, mas para fins práticos - por exemplo, para adicionar esses mesmos valores ao design. Milhares de pontos apenas desacelerarão o editor, mas ele não poderá exibir o resultado de qualquer maneira - em vez de linhas contínuas reais, haverá algum tipo de resultado da média dos pontos, feito como Deus colocaria uma alma.Portanto, chegou a hora de pensar em outro algoritmo - que daria imediatamente vetores. Como os editores comuns de linhas curvas oferecem apenas interpolação pelas curvas de Bezier, focaremos nelas.O algoritmo, de fato, é simples - e muito mais simples do que o descrito na primeira parte. Tomamos duas curvas de envelope, definimos o número de ondas que devem caber em 360 graus, estimamos em que ângulo e com que curvatura o guilhoché real deve ir do ponto atual para o próximo e interpola-o com quatro curvas de Bezier.Aqui está um programa no Asymptote, que é extremamente conveniente para essas coisas.import graph;
size(1000,1000);
xaxis(ticks=Ticks);
yaxis(ticks=Ticks);
defaultpen(2);
var zero = (0,0);
real tens(bool at_top, real angle)
{
return angle/180;
}
guide wave(path top, path bottom, int parts, real offset)
{
guide w;
real step = 1/parts;
real half = step/2;
pair[] top_pt;
pair[] bot_pt;
pair[] top_dir;
pair[] bot_dir;
real[] top_angle;
real[] bot_angle;
for(int i: sequence(0,parts-1))
{
real rel = i*step + step*offset;
real top_time = reltime(top, rel);
real bot_time = reltime(bottom, rel+half);
top_pt[i] = point(top, top_time);
bot_pt[i] = point(bottom, bot_time);
top_dir[i] = dir(top, top_time);
bot_dir[i] = dir(bottom, bot_time);
}
for(int i: sequence(0,parts-1))
{
int prev = i == 0 ? parts-1 : i-1;
int next = i == parts-1 ? 0 : i+1;
var v1 = bot_pt[i] - top_pt[i];
var v2 = bot_pt[prev] - top_pt[i];
var a = degrees(v2) - degrees(v1);
top_angle[i] = a<0 ? 360+a : a;
v1 = top_pt[i] - bot_pt[i];
v2 = top_pt[next] - bot_pt[i];
a = degrees(v2) - degrees(v1);
bot_angle[i] = a<0 ? 360+a : a;
}
for(int i: sequence(0,parts-1))
{
int next = i == parts-1 ? 0 : i+1;
var l1 = length(top_pt[i]--bot_pt[i]);
pair ctl1 = top_pt[i] + top_dir[i] * tens(true, top_angle[i]) * l1;
pair ctl2 = bot_pt[i] - bot_dir[i] * tens(false, bot_angle[i]) * l1;
w = w .. top_pt[i] .. controls ctl1 and ctl2 .. bot_pt[i];
var l2 = length(bot_pt[i]--top_pt[next]);
ctl1 = bot_pt[i] + bot_dir[i] * tens(false, bot_angle[i]) * l2;
ctl2 = top_pt[next] - top_dir[next] * tens(true, top_angle[next]) * l2;
w = w .. bot_pt[i] .. controls ctl1 and ctl2 .. top_pt[next];
}
return w;
}
void repeat(int count, path top, path bottom, int parts)
{
real step = 1/count;
for(int i: sequence(0, count-1))
{
draw(wave(top, bottom, parts, step*i));
}
}
path normalize(path p)
{
var min = min(p);
var max = max(p);
var top_center = min + ((max.x-min.x)/2, (max.y-min.y)/2);
return scale(20*1/(max-min).x)*shift(zero - top_center)*p;
}
path top = (338.499521684,-159.274266483)
..controls (327.252951684,-158.148796483) and (323.448961684,-145.618286483) .. (318.743661684,-137.260595483)
..controls (309.897671684,-123.808725483) and (292.025851684,-123.657732483) .. (278.251471684,-118.807470483)
..controls (272.669581684,-117.510629483) and (268.731931684,-109.221757483) .. (274.571781684,-105.645360483)
..controls (281.545351684,-101.031122483) and (290.488261684,-97.7906864833) .. (293.317871684,-89.0437964838)
..controls (296.611021684,-81.8498064838) and (293.894071684,-73.5853264838) .. (295.556161684,-66.3445764838)
..controls (299.563831684,-59.7686064838) and (308.181311684,-64.5344964838) .. (312.903811684,-67.4344264838)
..controls (325.368171684,-74.9872364838) and (341.157891684,-80.6126364838) .. (355.257331684,-73.9383264838)
..controls (363.506651684,-70.9246164838) and (370.115991684,-63.9703964838) .. (378.731941684,-62.0926264838)
..controls (384.688491684,-61.4010364838) and (389.980631684,-67.6129964838) .. (387.306161684,-73.3211464838)
..controls (385.256921684,-82.8346964838) and (388.441441684,-93.9447564833) .. (397.757331684,-98.3016064833)
..controls (403.144721684,-101.085582483) and (412.671611684,-104.606352483) .. (410.331551684,-112.414892483)
..controls (406.654931684,-119.718595483) and (396.921641684,-119.937732483) .. (390.144051684,-122.524267483)
..controls (378.065751684,-125.483516483) and (364.313841684,-130.717262483) .. (359.884541684,-143.562216483)
..controls (356.731021684,-151.157386483) and (350.818391684,-160.192046483) .. (341.435061684,-159.293796483)
..controls (340.456461684,-159.306096483) and (339.478031684,-159.281196483) .. (338.499521684,-159.274296483)
--cycle;
top = normalize(top);
bottom = scale(0.5)*top;
top = ellipse(zero, 4, 6);
bottom = ellipse(zero, 2, 3);
top = circle(zero, 5);
bottom = circle(zero, 3);
repeat(12, top, bottom, 8);
O caso mais compreensível é quando os sinusóides estão localizados entre dois círculos.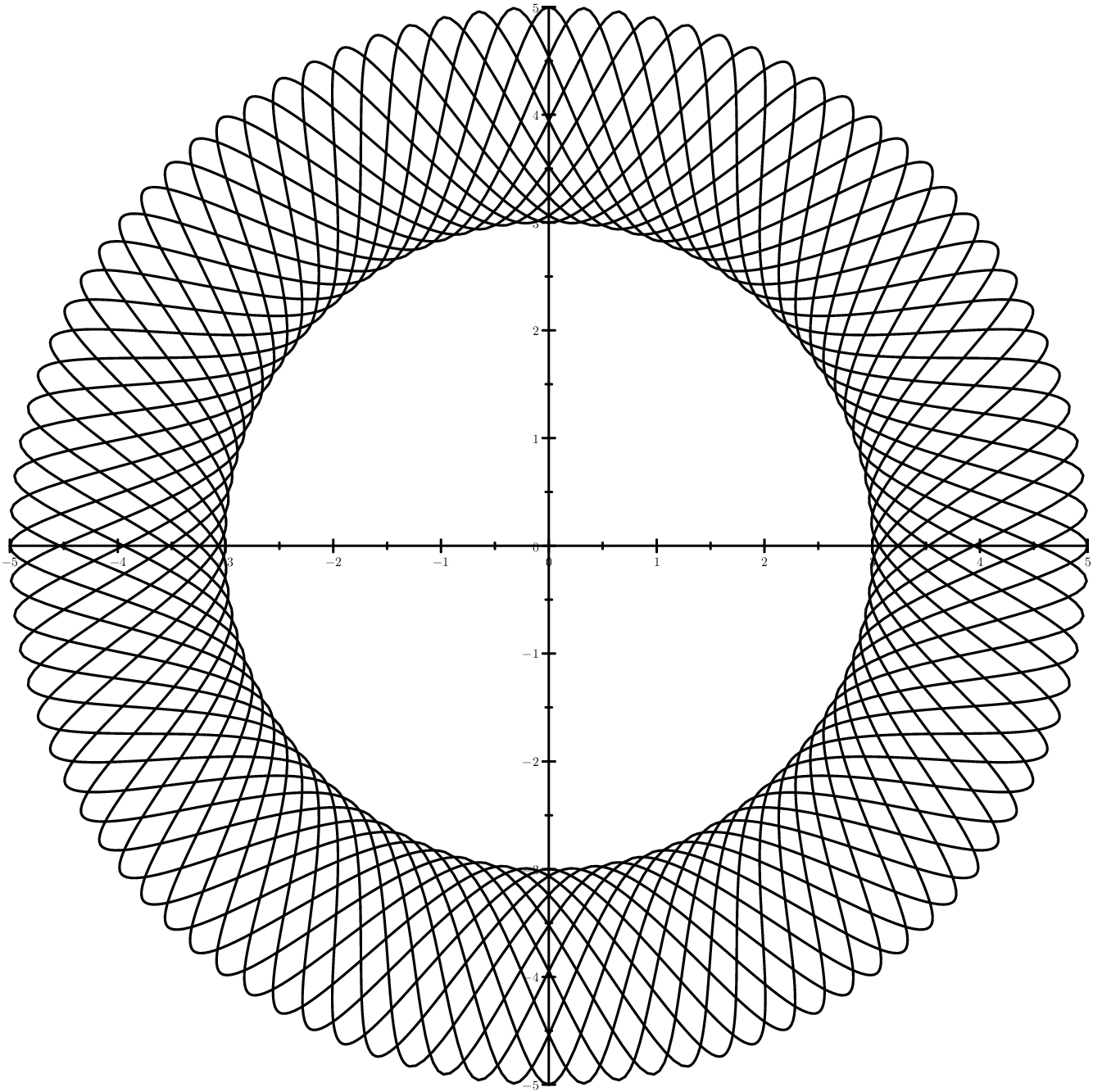
O caso é mais astuto - elipses em vez de círculos.
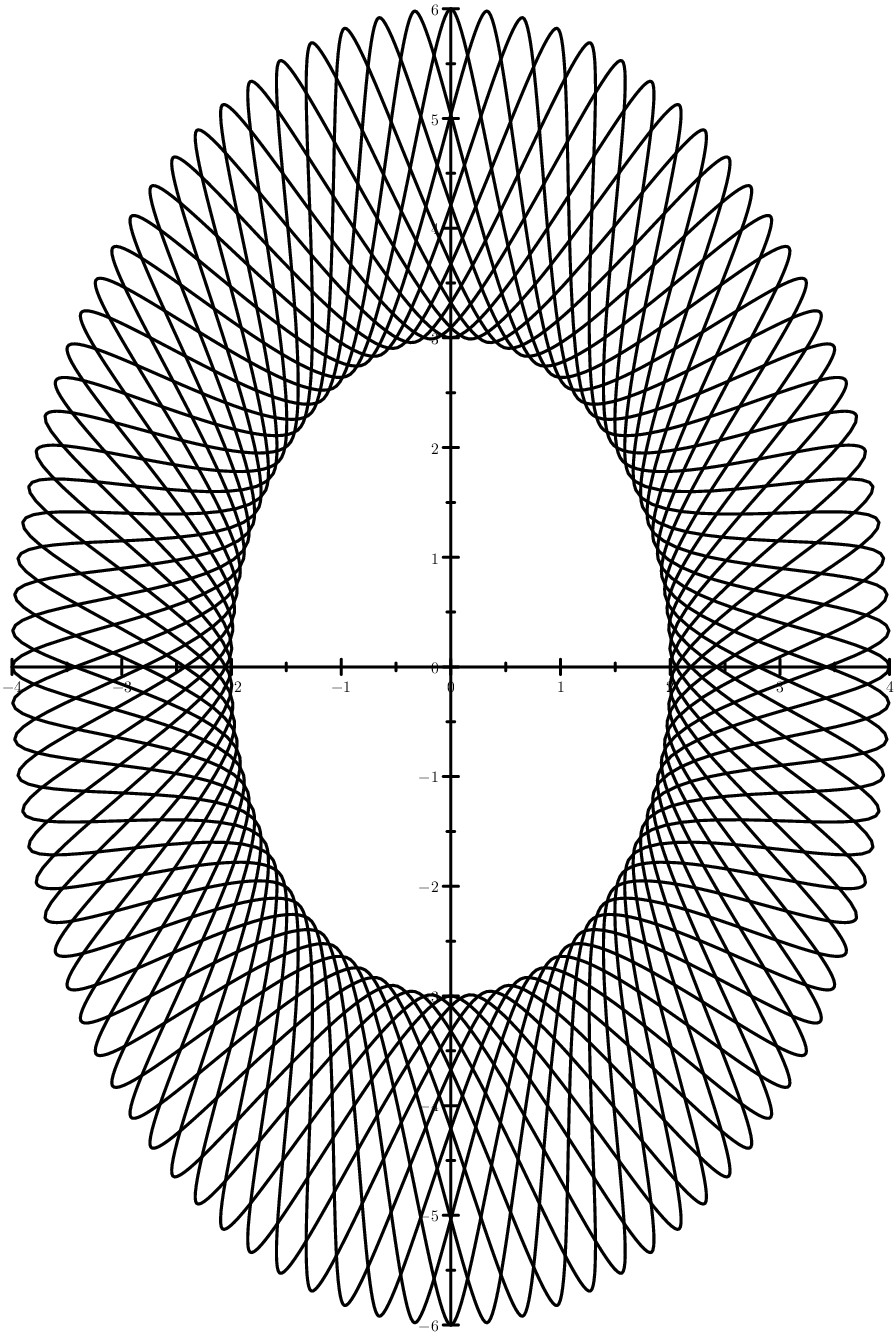E uma imagem próxima ao uso industrial: guilhoché, formando uma espécie de saída artística.
Aqui o resultado, no entanto, não é perfeito. Primeiro, a função dezenas teve que ser ajustada para que sempre retornasse uma “tensão” constante de 0,5. E segundo, as curvas não são muito simétricas e, na parte esquerda, perto do eixo X, elas são de alguma forma confusas. Claro, tudo isso pode ser corrigido manualmente, especialmente se você fizer notas para o estado e tiver artistas muito qualificados, mas você pode tentar aumentar a precisão dos cálculos, porque eles obviamente se perdem em alguns pontos em que a curvatura do envelope muda acentuadamente.Como os guilochés são interpolados, surge a pergunta: eles coincidem com, por assim dizer, "real", isto é, atraídos por pontos. Sendo novo na geometria diferencial, acho difícil dizer, mas sim "não" do que "sim".Mas quem realmente vê a diferença?E o benefício prático é inegável - com algumas dezenas de curvas de Bezier, o trabalho é muito mais fácil do que com mil pontos e eles abrem muito mais possibilidades de design.Além disso, esse algoritmo também pode ser aprimorado. Duas opções sugerem-se imediatamente:a) especificar um número diferente de pontos na curva externa e interna; assim, o efeito de triturar o padrão mais próximo do centro não será criado, como nos exemplos com um círculo e uma elipse.b) coloque os pontos nos envelopes de maneira não uniforme, mas, por exemplo, tornando-os mais frequentemente e com menos frequência, o que adicionará uma nova dimensão ao padrão.