Como eu parei de ter medo e escrevi um bot de jogo

Ou a boa e velha programação dinâmica sem essas redes neurais.

Há um ano e meio, participei de uma competição corporativa (para fins de entretenimento) ao escrever um bot para o jogo Lode Runner. Há 20 anos, resolvi diligentemente todos os problemas de programação dinâmica no curso correspondente, mas praticamente esqueci tudo e não tinha experiência em programar bots de jogos. Pouco tempo foi alocado, eu tinha que lembrar, experimentar em movimento e pisar independentemente no rake. Mas, de repente, tudo deu muito certo, então decidi sistematizar o material e não afogar o leitor com matan.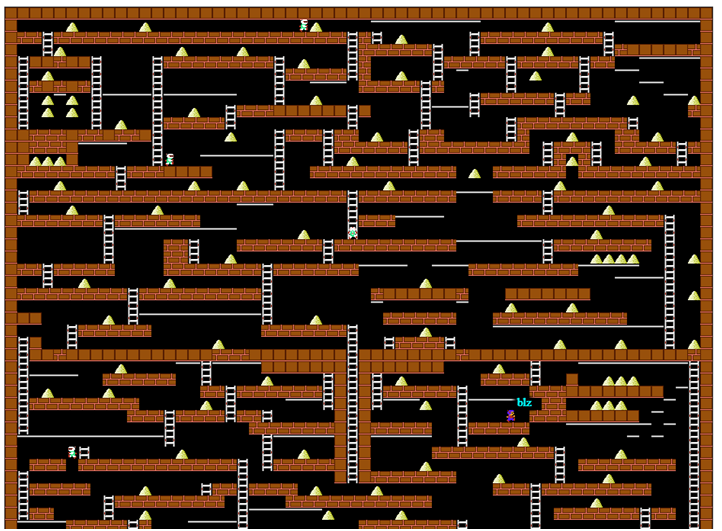


Tela do jogo do servidor do projeto Codenjoy

Para começar, descreveremos um pouco as regras do jogo : o jogador se move horizontalmente ao longo do chão ou através de canos, sabe subir e descer escadas, cai se não houver chão embaixo dele. Ele também pode fazer um furo para a esquerda ou para a direita, mas nem todas as superfícies podem ser cortadas - condicionalmente é possível um piso de “madeira” e concreto - não.

Monstros correm atrás do jogador, caem nos buracos e morrem neles. Mas o mais importante é que o jogador deve coletar ouro; no primeiro ouro coletado, ele recebe 1 ponto de lucro; no N-ésimo, recebe N pontos. Após a morte, o lucro total permanece, mas, pelo primeiro ouro, eles novamente dão 1 ponto. Isso sugere que o principal é permanecer vivo o maior tempo possível, e coletar ouro é de alguma forma secundária.

Como existem lugares no mapa que o jogador não pode sair de si mesmo, um suicídio gratuito foi introduzido no jogo, o que colocou o jogador aleatoriamente em algum lugar, mas na verdade interrompeu o jogo todo - o suicídio não interrompeu o crescimento no valor do ouro encontrado. Mas não abusaremos desse recurso.

Todos os exemplos do jogo serão apresentados em uma exibição simplificada, usada nos logs do programa: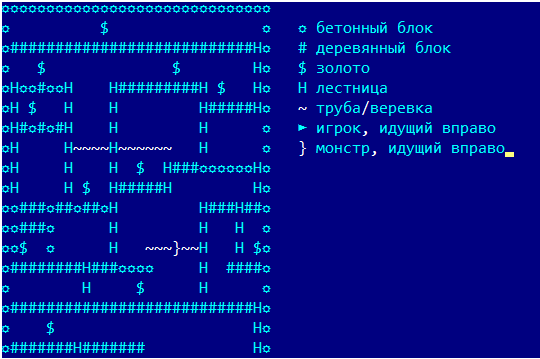

Pouco de teoria

Para implementar o bot usando algum tipo de matemática, precisamos definir alguma função objetiva que descreva as realizações do bot e encontrar ações para maximizá-lo. Por exemplo, para coletar ouro, obtemos +100, para morte -100500, portanto, nenhuma coleção de ouro mata a possível morte.

Uma pergunta separada e sobre o que exatamente determinamos a função objetivo, ou seja, Qual é o estado do jogo? No caso mais simples, as coordenadas do jogador são suficientes, mas no nosso tudo é muito mais complicado:

• coordenadas do jogador
• as coordenadas de todos os buracos perfurados por todos os jogadores
• as coordenadas de todo o ouro no mapa (ou as coordenadas de ouro comido recentemente)
• coordenadas de todos os outros jogadores

Parece assustador. Portanto, vamos simplificar um pouco a tarefa e até lembrarmos do ouro que comemos (voltaremos a isso mais tarde), também não lembraremos as coordenadas de outros jogadores e monstros.

Assim, o estado atual do jogo é:

• coordenadas do jogador
• coordenadas de todos os poços

As ações do jogador mudam de estado de maneira compreensível:

• Os comandos de movimento alteram uma das coordenadas correspondentes
• A equipe de escavação do poço adiciona um novo poço
• A queda de um jogador sem suporte reduz a coordenada vertical
• A inação do jogador em pé no suporte não altera o estado

Agora precisamos entender como maximizar a própria função. Um dos métodos clássicos veneráveis ​​para calcular o jogo N avança é a programação dinâmica. É impossível prescindir de fórmulas, portanto, eu as darei de forma simplificada. Você precisará introduzir muitas notações primeiro.

Para simplificar, manteremos o relatório de horário da movimentação atual, ou seja, o movimento atual é t = 0.
Denotamos o estado do jogo durante o curso de t por$$$x^t$.
Vários$$ denotará todas as ações válidas do bot (em um estado específico, mas, por simplicidade, não escreveremos o índice do estado), por meio de $$denotamos uma ação específica no curso t (omitimos o índice).
doença$$$x^t$ Sob a influência $$entra em estado $$$x^{t+1}_a$.

Ganhar quando a ação a estiver no estado$$$x^t$ nós o denotamos como $$$P(x^t, x^{t+1}_a)$. Ao calcular, assumimos que, se comemos ouro, é igual a G = 100, se eles morreram, então D = -100500, caso contrário, 0.

Deixe$$$F(x^t)$esta é a função de recompensa para o jogo ideal de um bot que está no estado x no momento t. Só precisamos encontrar uma ação que maximize$$$F(x^0)$.

Agora, escrevemos a primeira fórmula, que é muito importante e ao mesmo tempo quase correta:

$$

$$F(x^0) = \max_{a \in A} F(x^1_a) + P(x^0, x^1_a)$$

Ou para um ponto arbitrário no tempo

$$

$$F(x^t) = \max_{a \in A} F(x^{t+1}_a) + P(x^t, x^{t+1}_a)$$

Parece bastante desajeitado, mas o significado é simples - a solução ideal para o movimento atual consiste na solução ideal para o próximo movimento e no ganho no movimento atual. Esse é o princípio de otimidade tortuosamente formulado por Bellman. Não sabemos nada sobre os valores ótimos na etapa 1, mas se os conhecêssemos, encontraríamos uma ação que maximiza a função simplesmente iterando todas as ações do bot. A beleza das relações de recorrência é que podemos encontrar$$$F(x^1)$, aplicando o princípio de otimalidade, expressando-o exatamente na mesma fórmula através de $$$F(x^2)$. Também podemos expressar facilmente a função de pagamento em qualquer etapa.

Parece que o problema está resolvido, mas aqui estamos diante do problema de que, em cada etapa, tivemos que classificar as ações de 6 jogadores, na etapa N da recursão, teríamos que classificar as opções de 6 ^ N, que para N = 8 já é um número bastante decente ~ 1,6 milhões de casos. Por outro lado, temos microprocessadores gigahertz que não têm nada para fazer, e parece que eles vão lidar completamente com a tarefa, e limitaremos a profundidade da pesquisa a eles com exatamente 8 movimentos.

E assim, nosso horizonte de planejamento é de 8 movimentos, mas onde obter os valores$$$F(x^9)$? E aqui chegamos à ideia de que somos capazes de analisar de alguma forma as perspectivas da posição e atribuímos a ela algum valor com base em suas considerações mais altas. Deixe ser$$$F(x^9)=S(x^9)$Onde $$$S(x)$isso é uma função da estratégia, na versão mais simples é apenas uma matriz a partir da qual selecionamos o valor de acordo com as coordenadas geométricas do bot. Podemos dizer que os 8 primeiros movimentos foram uma tática, e então a estratégia começa. De fato, ninguém nos restringe na escolha de uma estratégia, e trataremos disso mais tarde, mas, por enquanto, para não nos tornarmos uma coruja de uma piada sobre lebres e ouriços, passaremos à tática.

Esquema geral

E assim, decidimos o algoritmo. Em cada etapa, resolvemos o problema de otimização, encontramos a ação ideal para a etapa, concluímos e depois o jogo prossegue para a próxima etapa.

É necessário resolver um novo problema a cada passo, porque a cada curso do jogo a tarefa muda um pouco, aparece novo ouro, alguém come alguém, os jogadores se mexem ...
Mas não pense que nosso engenhoso algoritmo pode fornecer tudo. Depois de resolver o problema de otimização, você deve definitivamente adicionar um manipulador que verificará situações desagradáveis:

• Permanente bot no lugar por um longo tempo
• Caminhada contínua esquerda-direita
• Falta de renda por muito tempo

Tudo isso pode exigir uma mudança radical de estratégia, suicídio ou alguma outra ação fora da estrutura do algoritmo de otimização. A natureza dessas situações pode ser diferente. Às vezes, as contradições entre estratégia e tática levam ao congelamento do bot em um ponto que lhe parece estrategicamente importante, que foi descoberto por botânicos antigos chamados Buridanov Donkey.



Seus oponentes podem congelar e fechar seu caminho curto até o cobiçado ouro - trataremos de tudo isso mais tarde.

A luta contra a procrastinação

Considere o caso simples quando um ouro está localizado à direita do bot e não há mais células de ouro em um raio de 8. Que passo o bot dará, guiado por nossa fórmula? De fato - absolutamente qualquer. Por exemplo, todas essas soluções oferecem exatamente o mesmo resultado, mesmo para três movimentos:

• passo à esquerda - passo à direita - passo à direita
• passo para a direita - inação - inação
• inação - inação - passo à direita

Todas as três opções dão uma vitória igual a 100, o bot pode escolher a opção com inação, na próxima etapa resolver o mesmo problema novamente, escolher a inação novamente ... E ficar parado para sempre. Precisamos modificar a fórmula para calcular os ganhos, a fim de estimular o bot a agir o mais cedo possível:

$$

$$F(x^0) = \max_{a \in A} F(x^1_a)*E + P(x^0, x^1_a)$$

multiplicamos o ganho futuro no próximo passo pelo "coeficiente de inflação" E, que deve ser escolhido menor que 1. Podemos experimentar com segurança valores de 0,95 ou 0,9. Mas não o escolha muito pequeno, por exemplo, com um valor de E = 0,5, o ouro consumido no 8º movimento trará apenas 0,39 pontos.

E assim, redescobrimos o princípio de "Não adie até amanhã o que você pode comer hoje".

Segurança

Coletar ouro certamente é bom, mas você ainda precisa pensar em segurança. Temos duas tarefas:

• Ensine o bot a cavar buracos se o monstro estiver em uma posição adequada
• Ensine o bot a fugir dos monstros

Mas não dizemos ao bot o que fazer, definimos o valor da função de lucro e o algoritmo de otimização escolherá as etapas apropriadas. Um problema separado é que não calculamos exatamente onde um monstro pode estar em um movimento específico. Portanto, por simplicidade, assumimos que os monstros estão no lugar e simplesmente não precisamos nos aproximar deles.

Se eles começarem a se aproximar de nós, o bot começará a fugir deles, porque será multado por estar muito perto deles (tipo de auto-isolamento). E assim, introduzimos duas regras:

• Se chegarmos ao monstro à distância d e d <= 3, uma multa de 100.500 * (4-d) / 4 é imposta a nós
• Se o monstro chegar perto o suficiente, estiver na mesma linha conosco e houver um buraco entre nós, obteremos algum lucro P

O conceito de "abordou o monstro à distância d" abriremos um pouco mais tarde, mas, por enquanto, vamos seguir para a estratégia.

Percorremos os gráficos

Matematicamente, o problema da evasão ideal do ouro é um problema resolvido há muito tempo de um vendedor ambulante, cuja solução não é um prazer. Mas antes de resolver esses problemas, você precisa pensar em uma pergunta simples - mas como você encontra a distância entre dois pontos no jogo? Ou de uma forma um pouco mais útil: para um determinado ouro e para qualquer ponto do mapa, encontre o número mínimo de movimentos pelos quais o jogador alcançará o ponto a partir do ouro. Por algum tempo, esqueceremos de cavar buracos e pular neles, deixaremos apenas movimentos naturais por 1 célula. Somente caminharemos na direção oposta - do ouro e do outro lado do mapa.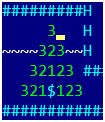



Na primeira etapa, selecionamos todas as células das quais podemos entrar em ouro em um movimento e as atribuímos a 1. Na segunda etapa, selecionamos todas as células das quais caímos em uma em uma etapa e as atribuímos a 2. A imagem mostra o caso por 3 etapas. Agora vamos tentar escrever tudo formalmente, em um formato adequado para programação.

Nós vamos precisar:

• A distância numérica bidimensional da matriz [x, y], na qual armazenaremos o resultado. Inicialmente, para coordenadas douradas, contém 0, para os pontos restantes -1.
• A matriz oldBorder, na qual armazenaremos os pontos dos quais nos moveremos, inicialmente ela possui um ponto com coordenadas douradas
• Matriz newBorder, na qual armazenaremos os pontos encontrados na etapa atual

1. Para cada ponto p de oldBorder, encontramos todos os pontos p_a dos quais podemos alcançar p em uma etapa (mais precisamente, apenas damos todos os passos possíveis de p na direção oposta, por exemplo, voando para cima na ausência de suporte) e distância [p_a] = - 1
2. Colocamos cada um desses pontos p_a na matriz newBorder, à distância [p_a] escrevemos o número da iteração
3. Após a conclusão de todos os pontos:
4. Troque as matrizes oldBorder e newBorder, após o que limpamos newBorder
5. Se oldBorder estiver vazio, termine o algoritmo, caso contrário, vá para a etapa 1.

A mesma coisa no pseudo-código:

iter=1;
newBorder.clear();
distance.fill(-1);
distance[gold]=0;
oldBorder.push(gold);

while(oldBorder.isNotEmpty()) {
  for (p: oldBorder){
    for (p_a: backMove(p)) {
      if (distance[p_a]==-1) {
         newBorder.push(p_a);
         distance[p_a]=iter;
      }
    }
  }
  Swap(newBorder, oldBorder);
  newBorder.clear();
  iter++;
}

Na saída do algoritmo, teremos um mapa de distância com o valor da distância de cada ponto de todo o campo do jogo ao ouro. Além disso, para pontos dos quais o ouro é inatingível, o valor da distância é -1. Os matemáticos chamam esse passeio pelo campo de jogo (que forma um gráfico com vértices nos pontos do campo e arestas que conectam os vértices acessíveis em um movimento) como "caminhar o gráfico na largura". Se implementássemos a recursão, em vez de duas matrizes de bordas, isso seria chamado de "percorrer o gráfico em profundidade", mas como a profundidade pode ser bastante grande (várias centenas), aconselho a evitar algoritmos recursivos ao percorrer gráficos.

O algoritmo real será um pouco mais complicado devido a cavar um buraco e pular nele - acontece que em 4 movimentos movemos uma célula para o lado e duas para baixo (desde que movemos na direção oposta e depois para cima), mas uma ligeira modificação do algoritmo resolve o problema.

Eu completei a figura com números, inclusive levando em consideração cavar um buraco e pular nele: o



que isso nos lembra?



O cheiro de ouro! E nosso bot vai buscar esse cheiro, como Rocky para queijo (mas, ao mesmo tempo, não perde o cérebro e se esquiva de monstros, e até faz buracos para eles). Vamos fazer dele uma estratégia simples e gananciosa:

1. Para cada ouro, construímos um mapa de distância e encontramos a distância para o jogador.
2. Escolha o ouro mais próximo do jogador e pegue sua carta para calcular a estratégia
3. Para cada célula do mapa, denote por d sua distância ao ouro, o valor estratégico
   

   $$

   $$S(x) = \begin{cases} 0 & \text{ $d < 0$,}\\ G_s E_s^d & \text{ $d \geq0$ } \end{cases}$$

Onde $$$G_s$se esse valor é imaginário do ouro, é desejável que ele seja avaliado várias vezes menos que o presente, e $$$E_s$este é um coeficiente de inflação <1, porque quanto mais o ouro imaginário é, mais barato é. A razão dos coeficientes E e$$$E_s$constitui um problema não resolvido do milênio e deixa espaço para a criatividade.

Não pense que nosso bot sempre será executado no ouro mais próximo. Suponha que tenhamos um ouro à esquerda a uma distância de 5 células e depois nulos, e à direita dois ouro a uma distância de 6 e 7. Como o ouro real é mais valioso do que se imaginava, o bot irá para a direita.

Antes de avançarmos para estratégias mais interessantes, faremos outra melhoria. No jogo, a gravidade puxa o jogador para baixo e ele só pode subir as escadas. Portanto, o ouro que é mais alto deve ser mais valorizado. Se a altura for relatada da linha superior para baixo, você poderá multiplicar o valor do ouro (com coordenadas verticais y) por$$$E_h^y$. Para coeficiente$$$E_h$ o novo termo “taxa de inflação vertical” foi cunhado, pelo menos não é usado pelos economistas e reflete bem a essência.

Estratégias complicadas

Com um ouro resolvido, você precisa fazer algo com todo o ouro, e eu não gostaria de atrair matemática pesada. Existe uma solução muito elegante, simples e incorreta (no sentido estrito) - se um ouro cria um "campo" de valor em torno de si, basta adicionar todos os campos de valor de todas as células com ouro em uma matriz e usá-lo como estratégia. Sim, essa não é uma solução ideal, mas várias unidades de ouro na distância média podem ser mais valiosas do que uma próxima.

No entanto, uma nova solução cria novos problemas - uma nova matriz de valor pode conter máximos locais, perto dos quais não há ouro. Como nosso bot pode entrar neles e não quer sair, isso significa que precisamos adicionar um manipulador que verifique se o bot está no máximo local da estratégia e permanece no lugar de acordo com os resultados da mudança. E agora temos uma ferramenta para combater os congelamentos - cancele essa estratégia com N movimentos e retorne temporariamente à estratégia do ouro mais próximo.

É muito engraçado ver como um bot preso muda sua estratégia e começa a cair continuamente, comendo todo o ouro mais próximo. Nos andares inferiores do mapa, o bot recupera os sentidos e tenta subir. Uma espécie de Dr. Jekyll e Sr. Hyde.

Estratégia discorda de táticas

Aqui, nosso bot chega ao ouro debaixo do chão:



ele já cai no algoritmo de otimização, resta dar três passos para a direita, abrir um buraco à direita e pular nele, e então a gravidade fará tudo sozinha. Algo assim:



Mas o bot congela no lugar. A depuração mostrou que não havia erro: o bot decidiu que a estratégia ideal era esperar um movimento e seguir a rota especificada e pegar ouro na última etapa analisada. No primeiro caso, ele recebe um ganho do ouro recebido e um ganho do ouro imaginário (na última iteração analisada, é apenas na célula onde o ouro estava), e no segundo - apenas do ouro real (embora uma vez antes), mas o ganho não há mais estratégia, porque o lugar embaixo do ouro está podre e não é promissor. Bem, no próximo passo, ele novamente decide fazer uma pausa um passo, já resolvemos esses problemas.

Eu tive que modificar a estratégia - já que memorizamos todo o ouro consumido na fase de análise, subtraindo as cartas de valor do ouro consumido da matriz total de valor estratégico, portanto, a estratégia levou em consideração a obtenção de táticas (era possível calcular o valor de maneira diferente - adicionando matrizes apenas para ouro inteiro, mas é computacionalmente mais complicado, porque há muito mais ouro no mapa do que podemos comer em 8 movimentos).

Mas isso não acabou com o nosso tormento. Suponha que a matriz de valor estratégico tenha um máximo local e o bot aproximou-se dela por 7 movimentos. O bot irá congelar? Não, porque para qualquer rota em que o bot atinja o máximo local em 8 jogadas, a vitória será a mesma. Boa e velha procrastinação. A razão pela qual é que o ganho estratégico não depende do momento em que nos encontramos na célula. A primeira coisa que vem à mente é multar o bot por um simples, mas isso não ajuda em nada de andar sem sentido para a esquerda / direita. É necessário tratar a causa raiz - levar em consideração o ganho estratégico a cada turno (como a diferença entre o valor estratégico dos estados novo e atual), reduzindo-o ao longo do tempo por um fator.
Essa. introduza um termo adicional na expressão para ganhar:

$$

$$p_{new}(x^0,x^1_a) = p(x^0,x^1_a) + (S(x^1_a) – S(x^0)).$$

o valor da função objetivo nesta última é geralmente considerado zero: $$$F(x^9) =0$. Como o ganho é depreciado a cada movimento, multiplicando por um coeficiente, isso fará com que o nosso bot obtenha um ganho estratégico mais rápido e elimine o problema observado.

Estratégia não testada

Não testei essa estratégia na prática, mas parece promissora.

1. Como sabemos todas as distâncias entre os pontos de ouro e as distâncias entre o ouro e o jogador, podemos encontrar a cadeia jogador-N de células de ouro (onde N é pequeno, por exemplo, 5 ou 6) com o menor comprimento. Até a busca mais simples do tempo é suficiente.
2. Selecione o primeiro ouro nesta cadeia e use seu campo de valor como uma matriz de estratégia.

Nesse caso, é desejável reduzir o custo real e o custo do ouro imaginário para que o bot não corra para o porão até o ouro mais próximo.

Melhorias finais

Depois que aprendemos a "espalhar-se" no mapa, vamos fazer uma "propagação" semelhante de cada monstro por vários movimentos e encontrar todas as células nas quais o monstro pode terminar, juntamente com o número de movimentos pelos quais ele será executado. Isso permitirá que o jogador rasteje pelo cano sobre a cabeça do monstro com total segurança.

E o último momento - ao calcular a estratégia e o valor imaginário do ouro, não levamos em conta a posição dos outros jogadores, simplesmente "os apagando" ao analisar o mapa. Acontece que conchas suspensas individuais podem bloquear o acesso a regiões inteiras; portanto, um manipulador adicional foi adicionado - para rastrear oponentes congelados e substituí-los por blocos de concreto durante a análise.

Recursos de implementação

Como o algoritmo principal é recursivo, devemos ser capazes de alterar rapidamente os objetos de estado e devolvê-los aos seus originais para modificações adicionais. Eu usei o java, uma linguagem com coleta de lixo, experimentar milhões de alterações relacionadas à criação de objetos de vida curta pode causar várias coleta de lixo em um turno do jogo, o que pode ser fatal em termos de velocidade. Portanto, é preciso ter muito cuidado nas estruturas de dados utilizadas, usei apenas matrizes e listas. Bem, ou use o projeto Valgala por sua própria conta e risco :)

Código Fonte e Servidor de Jogo

O código fonte pode ser encontrado aqui no github . Não julgue estritamente, muito foi feito às pressas. O servidor de jogos codenjoy fornecerá a infraestrutura para o lançamento de bots e o monitoramento do jogo. No momento da criação, a revisão era relevante, a revisão 1.0.26 foi usada.

Você pode iniciar o servidor com a seguinte linha:

call mvn -DMAVEN_OPTS=-Xmx1024m -Dmaven.test.skip=true clean jetty:run-war -Dcontext=another-context -Ploderunner

O projeto em si é extremamente curioso, oferece jogos para todos os gostos.

Conclusão

Se você leu tudo isso até o fim, sem preparação preliminar e entendeu tudo, então você é um sujeito raro.