🍃 👙 👩🏽‍🎓 A que prestamos atenção ao calcular a significância estatística do teste A / B 🏽 🔭 🚵🏻

No Uchi.ru, tentamos implementar até pequenas melhorias com o teste A / B, houve mais de 250 durante este ano acadêmico.O teste A / B é uma poderosa ferramenta de teste de alterações, sem a qual é difícil imaginar o desenvolvimento normal de um produto da Internet. Ao mesmo tempo, apesar da aparente simplicidade, ao realizar um teste A / B, erros graves podem ser cometidos tanto na fase de design do experimento quanto na soma dos resultados. Neste artigo, falarei sobre alguns dos aspectos técnicos do teste: como determinamos o período do teste, resumimos e como evitar resultados errôneos quando os testes são concluídos antes do previsto e ao testar várias hipóteses ao mesmo tempo.

Um esquema de teste A / B típico para nós (e para muitos) é assim:

Estamos desenvolvendo um recurso, mas antes de lançá-lo para todo o público, queremos garantir que ele melhore a métrica de destino, por exemplo, o envolvimento.
Determinamos o período para o qual o teste é iniciado.
Dividimos aleatoriamente os usuários em dois grupos.
Mostramos a um grupo a versão do produto com recursos (grupo experimental), o outro - o antigo (controle).
No processo, monitoramos a métrica para interromper um teste particularmente malsucedido no tempo.
Após o término do teste, comparamos a métrica nos grupos experimental e controle.
Se a métrica no grupo experimental for estatisticamente significativamente melhor do que no grupo controle, lançamos o recurso testado. Se não houver significância estatística, finalizamos o teste com um resultado negativo.

Tudo parece lógico e simples, o diabo, como sempre, nos detalhes.

Significância estatística, critérios e erros

Existe um elemento aleatório em qualquer teste A / B: as métricas de grupo dependem não apenas de sua funcionalidade, mas também do que os usuários entraram nelas e como se comportam. Para tirar conclusões confiáveis sobre a superioridade de um grupo, você precisa coletar observações suficientes no teste, mas mesmo assim você não está imune a erros. Eles são diferenciados por dois tipos:

Um erro do primeiro tipo ocorre se resolvermos a diferença entre os grupos, embora, na realidade, ela não exista. O texto também conterá um termo equivalente - um resultado falso positivo. O artigo é dedicado a esses erros.
Um erro do segundo tipo ocorre se corrigirmos a ausência de uma diferença, embora de fato seja.

Com um grande número de experimentos, é importante que a probabilidade de um erro do primeiro tipo seja pequena. Pode ser controlado usando métodos estatísticos. Por exemplo, queremos que a probabilidade de um erro do primeiro tipo em cada experimento não exceda 5% (esse é apenas um valor conveniente, você pode usar outro para suas próprias necessidades). Em seguida, realizaremos experimentos com um nível de significância de 0,05:

Existe um teste A / B com o grupo controle A e o grupo experimental B. O objetivo é verificar se o grupo B difere do grupo A em alguma métrica.
Formulamos a hipótese estatística nula: os grupos A e B não diferem, e as diferenças observadas são explicadas pelo ruído. Por padrão, sempre pensamos que não há diferença até que o contrário seja provado.
Verificamos a hipótese com uma regra matemática estrita - um critério estatístico, por exemplo, o critério do aluno.
Como resultado, obtemos o valor p. Está no intervalo de 0 a 1 e significa a probabilidade de ver a diferença atual ou mais extrema entre os grupos, desde que a hipótese nula seja verdadeira, ou seja, na ausência de diferença entre os grupos.
O valor de p é comparado com um nível de significância de 0,05. Se for maior, aceitamos a hipótese nula de que não há diferenças; caso contrário, acreditamos que haja uma diferença estatisticamente significante entre os grupos.

Uma hipótese pode ser testada com um critério paramétrico ou não paramétrico. Os paramétricos baseiam-se nos parâmetros da distribuição amostral de uma variável aleatória e têm mais poder (cometem erros do segundo tipo com menos frequência), mas impõem requisitos à distribuição da variável aleatória em estudo.

O teste paramétrico mais comum é o teste de Student. Para duas amostras independentes (caso de teste A / B), às vezes é chamado de critério de Welch. Este critério funciona corretamente se as quantidades estudadas forem distribuídas normalmente. Pode parecer que em dados reais esse requisito quase nunca é atendido, mas, na verdade, o teste exige uma distribuição normal das médias das amostras, não das próprias amostras. Na prática, isso significa que o critério pode ser aplicado se você tiver muitas observações em seu teste (dezenas a centenas) e não houver caudas muito longas nas distribuições. A natureza da distribuição das observações iniciais não é importante. O leitor pode verificar independentemente se o critério Student funciona corretamente, mesmo em amostras geradas a partir de Bernoulli ou em distribuições exponenciais.

Dos critérios não paramétricos, o critério de Mann-Whitney é popular. Deve ser usado se suas amostras forem muito pequenas ou apresentarem valores discrepantes grandes (o método compara as medianas, portanto, é resistente a discrepantes). Além disso, para que o critério funcione corretamente, as amostras devem ter poucos valores correspondentes. Na prática, nunca tivemos que aplicar critérios não paramétricos, em nossos testes sempre usamos o critério do aluno.

O problema do teste de múltiplas hipóteses

O problema mais óbvio e mais simples: se no teste houver vários grupos experimentais além do grupo controle, a soma dos resultados com um nível de significância de 0,05 levará a um aumento múltiplo na proporção de erros do primeiro tipo. Isso ocorre porque, com cada aplicação do critério estatístico, a probabilidade de um erro do primeiro tipo será de 5%. Com o número de grupos

n g r o u p s

$ngroups$ e nível de significância

α

$\alpha$ a probabilidade de algum grupo experimental vencer por acaso é:

P (a n y f a l s e p o s i t i v e) = 1 - (1 - α)^{n g r o u p s}

$P(any\ false\ positive) = 1 − (1 − \alpha) ^ {ngroups}$

Por exemplo, para os três grupos experimentais, obtemos 14,3% em vez dos 5% esperados. O problema é resolvido pela correção de Bonferroni para o teste de múltiplas hipóteses: você só precisa dividir o nível de significância pelo número de comparações (ou seja, grupos) e trabalhar com ele. Para o exemplo acima, o nível de significância, considerando a alteração, será de 0,05 / 3 = 0,0167 e a probabilidade de pelo menos um erro do primeiro tipo será aceitável 4,9%.

Método Hill - Bonferroni

— , , , .

n g r o u p s

$ngroups$ p-value ,

s t e p_n u m b e r

$step\_number$ :

α_{s t e p} = \frac{α}{n g r o u p s - s t e p_n u m b e r + 1}

$\alpha_{step} = \frac {\alpha} {ngroups − step\_number + 1}$

P-value

α / n g r o u p s

$\alpha/ngroups$ . , p-value

α / (n g r o u p s - 1)

$\alpha/(ngroups − 1)$ , . - , . ( , ) p-value, . A/B- — , — .

A rigor, as comparações de grupos por diferentes métricas ou seções da audiência também estão sujeitas ao problema de vários testes. Formalmente, é bastante difícil levar em consideração todas as verificações, porque é difícil prever com antecedência o número delas e, às vezes, elas não são independentes (principalmente quando se trata de métricas diferentes, não de fatias). Não existe uma receita universal, confie no bom senso e lembre-se de que, se você verificar várias fatias usando métricas diferentes, em qualquer teste poderá ver um resultado supostamente estatisticamente significativo. Portanto, é preciso ter cuidado, por exemplo, com o aumento significativo na retenção do quinto dia de novos usuários móveis das grandes cidades.

Peeping problem

Um caso particular de teste de múltiplas hipóteses é o problema de espreitar. O ponto é que o valor de p durante o teste pode cair acidentalmente abaixo do nível de significância aceito. Se você monitorar cuidadosamente o experimento, poderá capturar esse momento e cometer um erro sobre a significância estatística.

Suponha que nos afastamos da configuração de teste descrita no início do post e decidimos fazer um balanço com um nível de significância de 5% todos os dias (ou apenas mais de uma vez durante o teste). Resumindo, entendo que o teste é positivo se o valor de p estiver abaixo de 0,05 e sua continuação de outra forma. Com essa estratégia, a parcela de resultados falso-positivos será proporcional ao número de cheques e, no primeiro mês, alcançará 28%. Uma diferença tão grande parece contra-intuitiva, portanto, nos voltamos para a metodologia de testes A / A, indispensável para o desenvolvimento de esquemas de testes A / B.

A ideia de um teste A / A é simples: simular muitos testes A / B em dados aleatórios com agrupamento aleatório. Obviamente, não há diferença entre os grupos; portanto, você pode estimar com precisão a proporção de erros do primeiro tipo no seu esquema de teste A / B. O gif abaixo mostra como o valor de p muda de dia para quatro desses testes. Um nível de significância igual a 0,05 é indicado por uma linha tracejada. Quando o valor p cai abaixo, colorimos o gráfico de teste em vermelho. Se nesse momento os resultados do teste fossem resumidos, seria considerado bem-sucedido.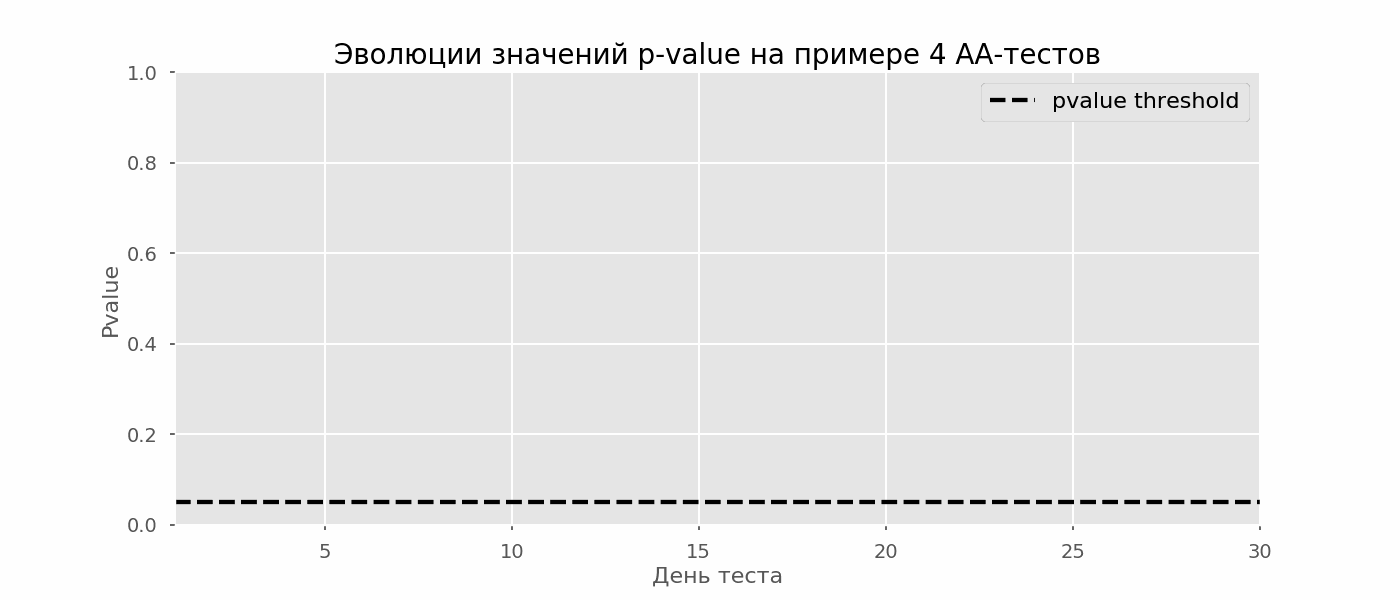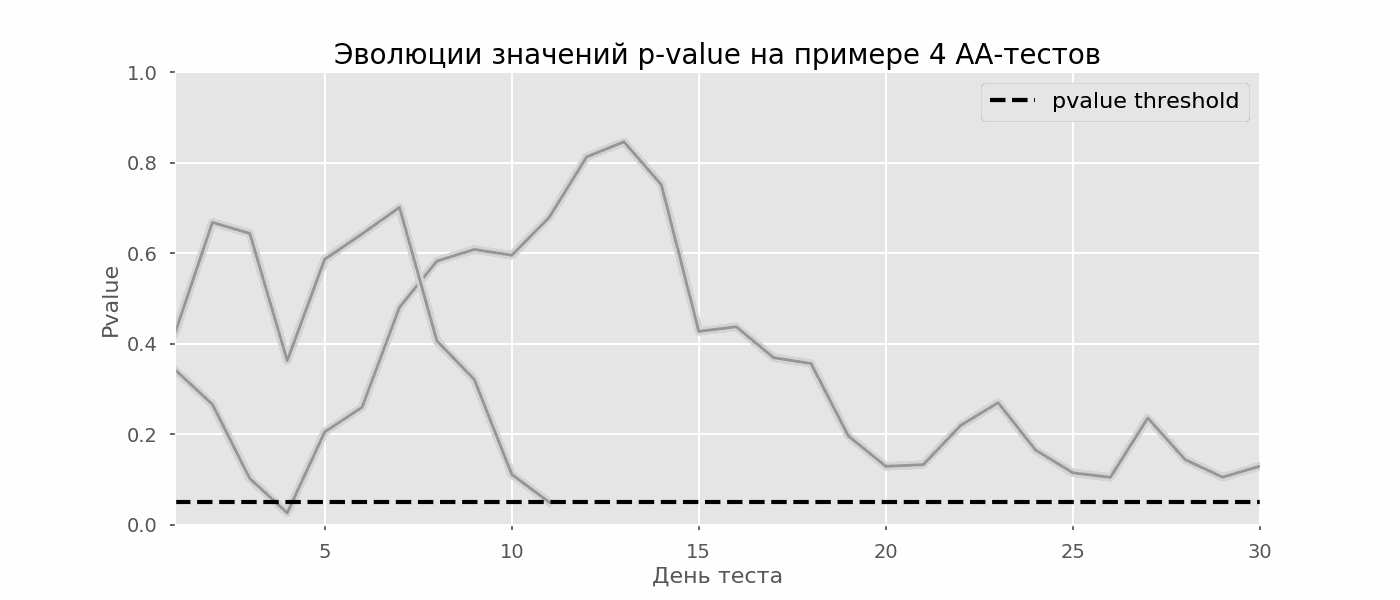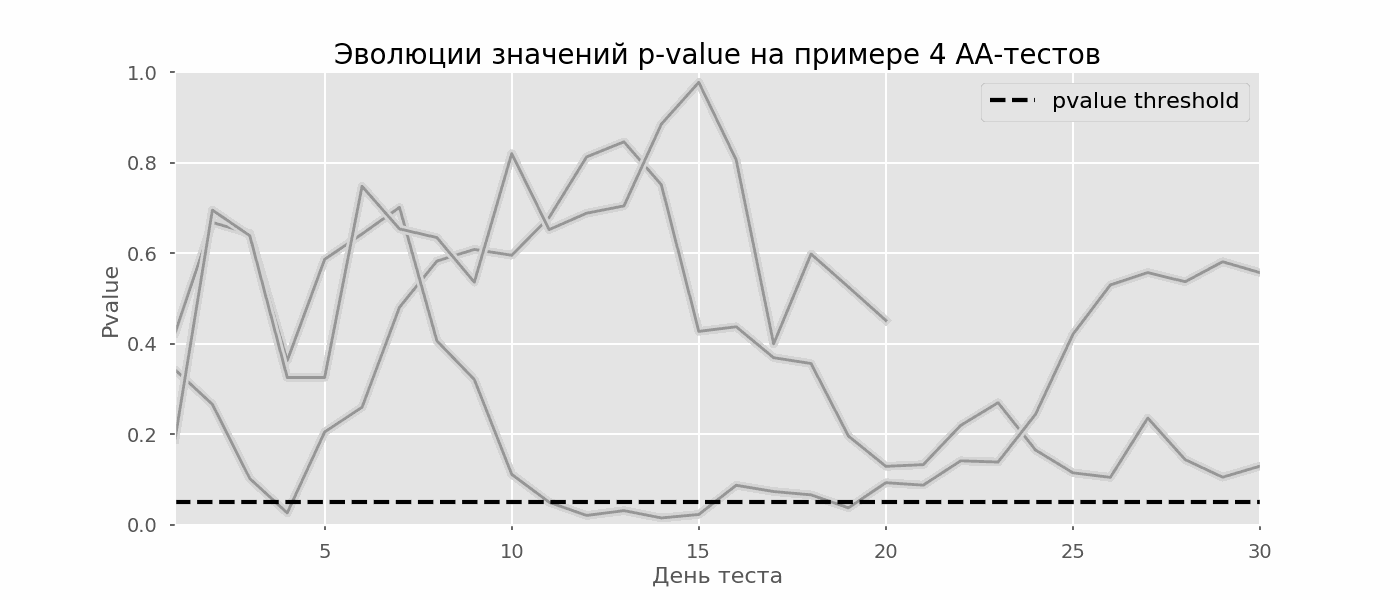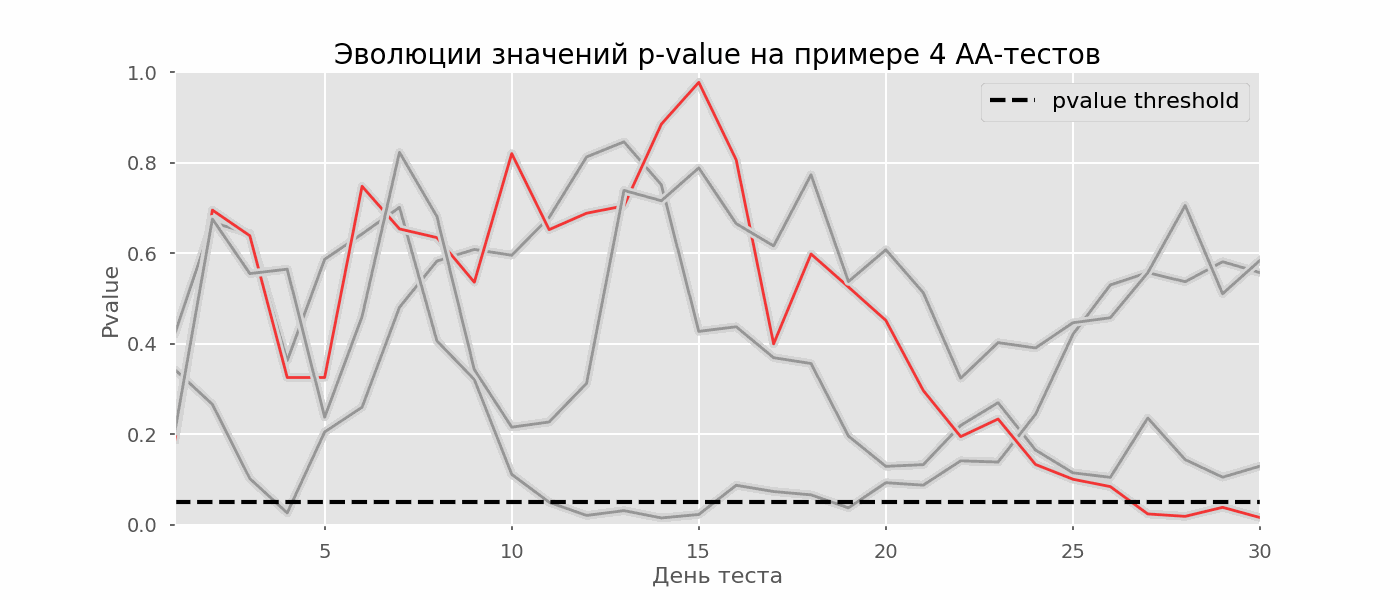

Da mesma forma, calculamos 10 mil testes A / A com duração de um mês e comparamos as frações de resultados falso-positivos no esquema com a soma no final do período e todos os dias. Para maior clareza, aqui estão os horários errantes de valor p por dia para as primeiras 100 simulações. Cada linha é o valor p de um teste, as trajetórias dos testes são destacadas em vermelho, que, como resultado, são erroneamente consideradas bem-sucedidas (quanto menor, melhor), a linha pontilhada é o valor-p necessário para reconhecer o teste como bem-sucedido.

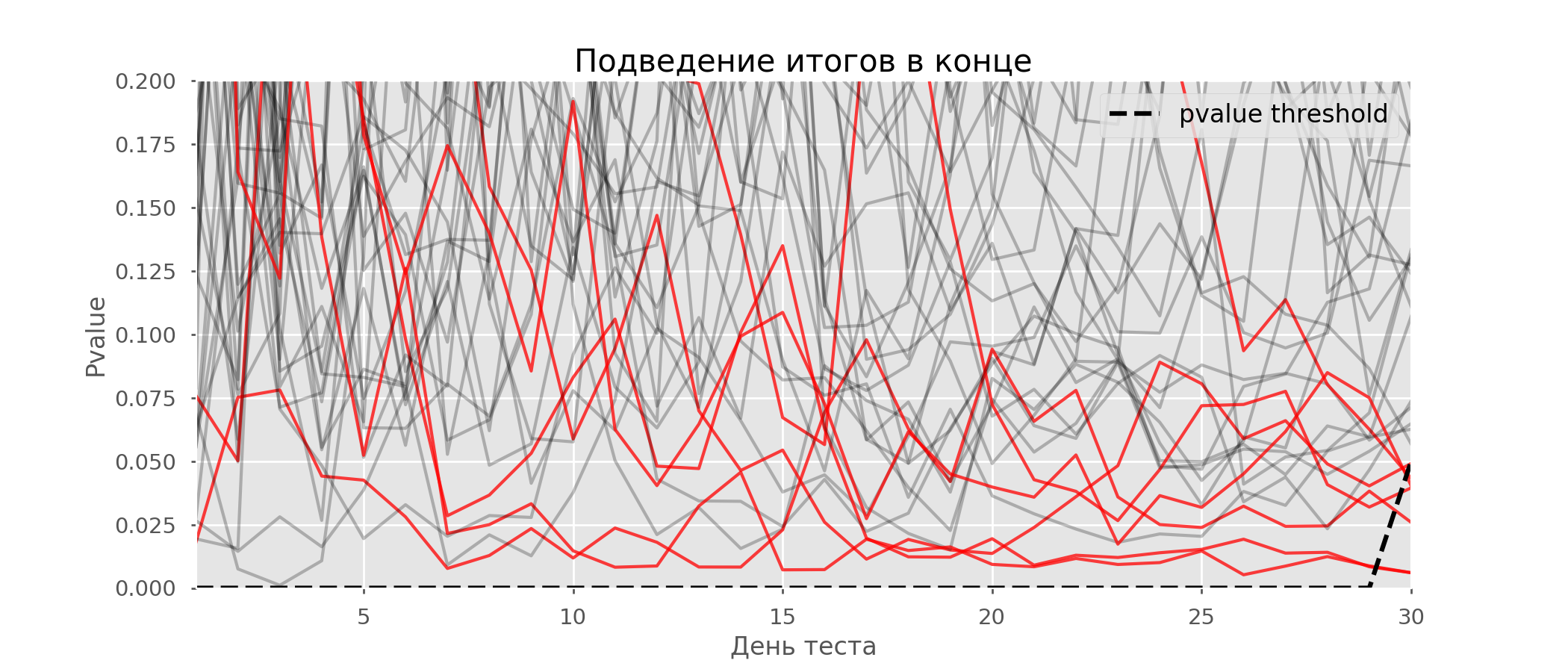No gráfico, você pode contar 7 testes falso-positivos e, no total, entre 10 mil, havia 502, ou 5%. Deve-se notar que o valor p de muitos testes durante o curso das observações caiu abaixo de 0,05, mas ao final das observações foi além do nível de significância. Agora vamos avaliar o esquema de teste com uma interrogação todos os dias:

Existem tantas linhas vermelhas que nada está claro. Vamos redesenhar quebrando as linhas de teste assim que seu valor-p atingir um valor crítico: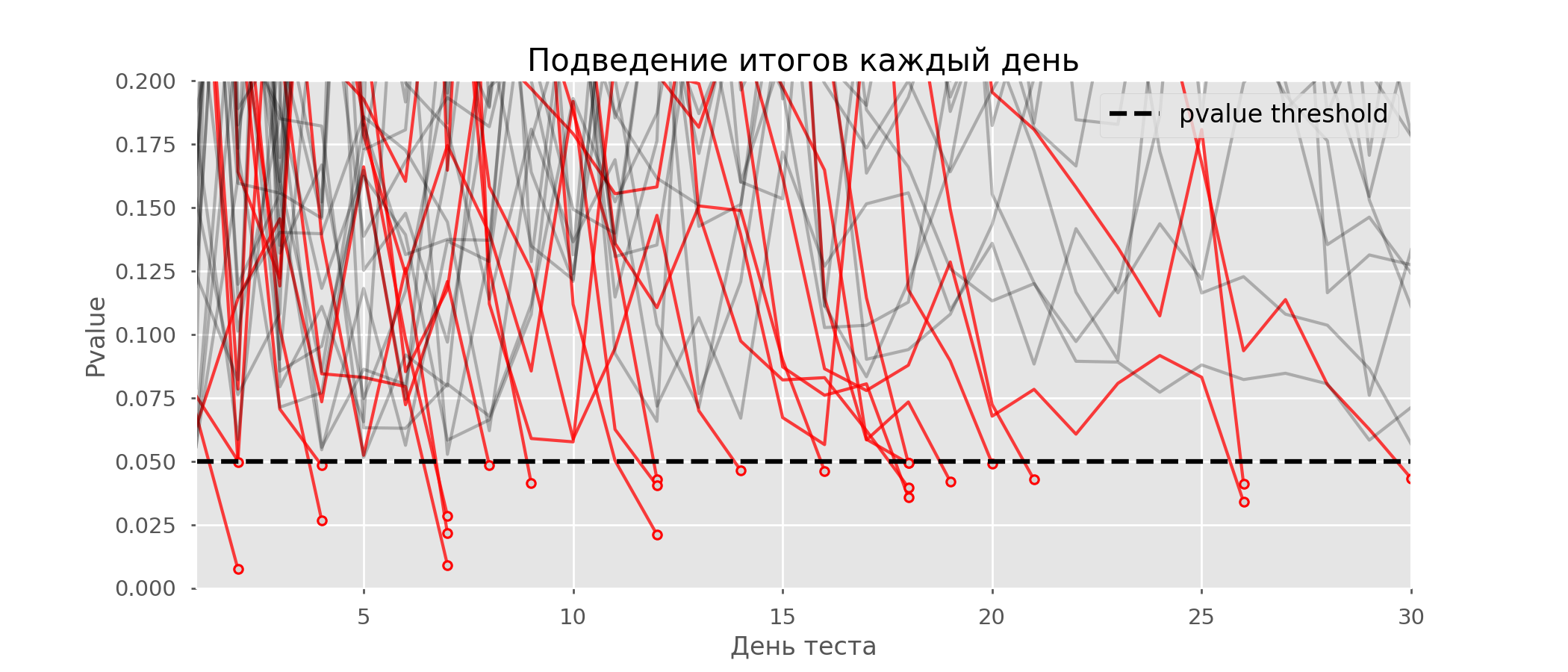

haverá um total de 2813 testes de falsos positivos em 10 mil, ou 28%. É claro que esse esquema não é viável.

Embora o problema de espiar seja um caso especial de vários testes, não vale a pena aplicar correções padrão (Bonferroni e outras), porque elas acabarão sendo excessivamente conservadoras. O gráfico abaixo mostra a porcentagem de resultados positivos falsos, dependendo do número de grupos testados (linha vermelha) e do número de espreitadelas (linha verde).

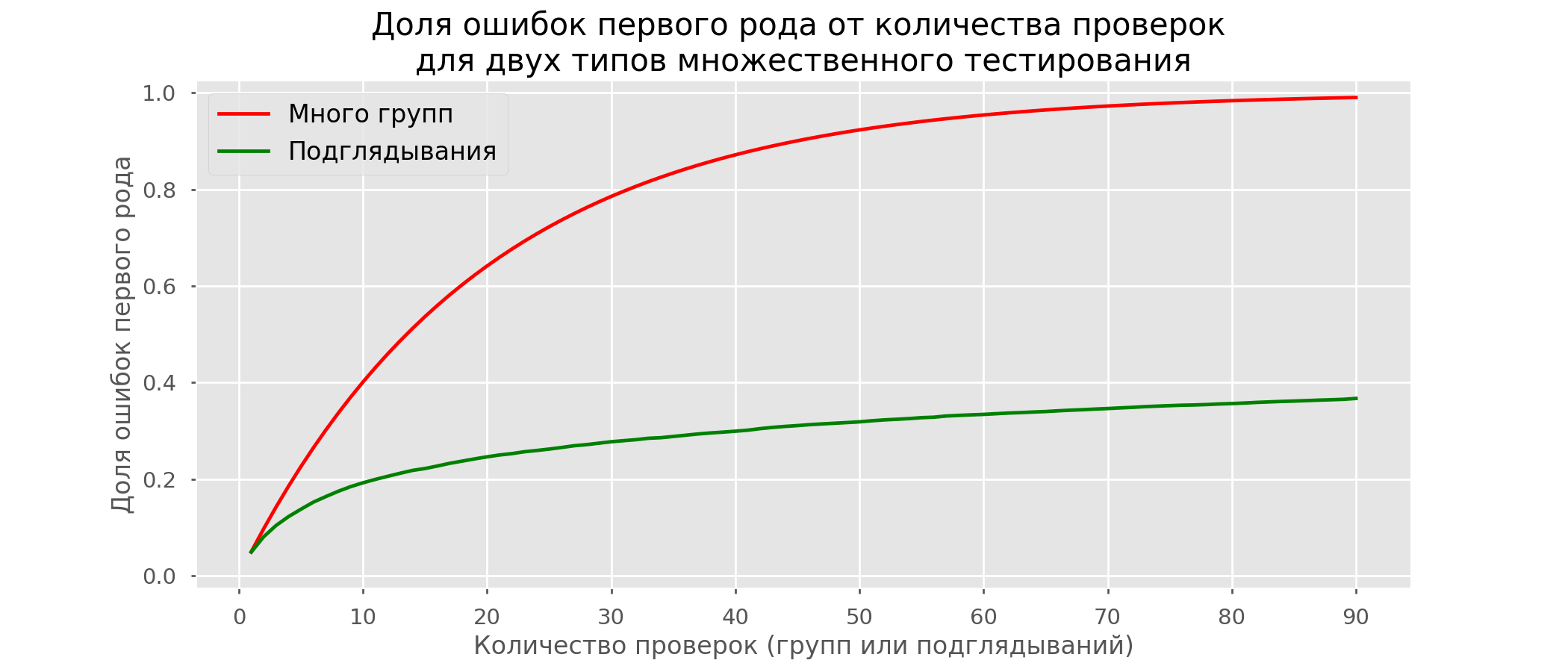Embora no infinito e na espiada cheguemos perto de 1, a proporção de erros cresce muito mais lentamente. Isso ocorre porque as comparações nesse caso não são mais independentes.

Abordagem bayesiana e o problema da espionagem

, A/B- . , . .

Métodos de Teste Inicial

Existem opções de teste que permitem fazer o teste prematuramente. Vou falar sobre dois deles: com um nível constante de significância (correção de Pocock) e dependente do número de espreitadelas (correção de O'Brien-Fleming). A rigor, para as duas correções, é necessário conhecer antecipadamente o período máximo do teste e o número de verificações entre o início e o final do teste. Além disso, as verificações devem ocorrer em intervalos aproximadamente iguais de tempo (ou em quantidades iguais de observações).

Pocock

O método é resumir os resultados dos testes todos os dias, mas com um nível de significância reduzido (mais rigoroso). Por exemplo, se soubermos que não faremos mais de 30 verificações, o nível de significância deve ser definido como 0,006 (selecionado dependendo do número de espreitadelas usando o método de Monte Carlo, ou seja, empiricamente). Em nossa simulação, obtemos 4% de resultados positivos falsos - aparentemente, o limite pode ser aumentado.

Apesar da aparente ingenuidade, algumas grandes empresas usam esse método específico. É muito simples e confiável se você tomar decisões sobre métricas confidenciais e muito tráfego. Por exemplo, no Avito, por padrão , o nível de significância é definido como 0,005 .

O'Brien-Fleming

Nesse método, o nível de significância varia de acordo com o número de verificação. É necessário determinar antecipadamente o número de etapas (ou espreitadelas) no teste e calcular o nível de significância para cada uma delas. Quanto mais cedo tentarmos concluir o teste, mais rigorosos serão os critérios. Limiares de estatísticas do aluno

Z_{s t e p}

$Z_{step}$ (incluindo o valor na última etapa

Z_{l a s t_s t e p}

$Z_{last\_step}$ ) correspondente ao nível de significância desejado depende do número de verificação

s t e p_n u m b e r

$step\_number$ (leva valores de 1 ao número total de verificações

t o t a l_s t e p s

$total\_steps$ inclusive) e são calculados de acordo com a fórmula empiricamente obtida:

Z_{l a s t_s t e p} = 2.2471 + \frac{0.3373}{t o t a l_s t e p s} - \frac{0.6331}{\sqrt{t o t a l_s t e p s}} Z_{s t e p} = Z_{l a s t_s t e p} \sqrt{\frac{t o t a l_s t e p s}{s t e p_n u m b e r}}

$Z_{last\_step} = 2.2471 + \frac {0.3373} {total\_steps} − \frac {0.6331} {\sqrt {total\_steps}} \\ Z_{step} = Z_{last\_step} \ {\sqrt { \frac {total\_steps} {step\_number}}}$

Código de probabilidades

from sklearn.linear_model import LinearRegression
from sklearn.metrics import explained_variance_score
import matplotlib.pyplot as plt

# datapoints from https://www.aarondefazio.com/tangentially/?p=83
total_steps = [
    2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60
]
last_z = [
    1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081, 
    2.107, 2.123, 2.134, 2.143, 2.164, 2.17
]
features = [
    [1/t, 1/t**0.5] for t in total_steps
]
lr = LinearRegression()
lr.fit(features, last_z)
print(lr.coef_)  # [ 0.33729346, -0.63307934]
print(lr.intercept_)  # 2.247105015502784
print(explained_variance_score(lr.predict(features), last_z))  # 0.999894

total_steps_extended = np.arange(2, 80)
features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ]
plt.plot(total_steps_extended, lr.predict(features_extended))
plt.scatter(total_steps, last_z, s=30, color='black')
plt.show()

Os níveis de significância relevantes são calculados através do percentil

p e r c

$perc$ distribuição padrão correspondente ao valor das estatísticas do aluno

Z

$Z$ :

perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2

Nas mesmas simulações, é assim:

os resultados falso-positivos foram 501 em 10 mil, ou os 5% esperados. Observe que o nível de significância não atinge um valor de 5%, mesmo no final, pois esses 5% devem ser "manchados" em todas as verificações. Na empresa, usamos essa mesma correção se fizermos um teste com a possibilidade de uma parada antecipada. Você pode ler sobre a mesma e outras alterações aqui .

Método Optimizely

Optimizely , , . , . , . O'Brien-Fleming’a .

Calculadora de Teste A / B

As especificidades do nosso produto são tais que a distribuição de qualquer métrica varia muito, dependendo do público do teste (por exemplo, número da turma) e da época do ano. Portanto, não será possível aceitar as regras para a data final do teste com o espírito de "o teste terminará quando 1 milhão de usuários forem digitados em cada grupo" ou "o teste terminará quando o número de tarefas resolvidas atingir 100 milhões". Ou seja, funcionará, mas, na prática, para isso, será necessário levar em consideração muitos fatores:

que classes entram no teste;
o teste é distribuído para professores ou alunos;
época do ano acadêmico;
teste para todos os usuários ou apenas para novos.

No entanto, em nossos esquemas de teste A / B, você sempre precisa fixar a data final com antecedência. Para prever a duração do teste, desenvolvemos um aplicativo interno - calculadora de teste A / B. Com base na atividade dos usuários do segmento selecionado no ano passado, o aplicativo calcula o período durante o qual o teste deve ser executado para corrigir significativamente a elevação em X% pela métrica selecionada. A correção para vários testes também é automaticamente levada em consideração e os níveis de significância do limiar são calculados para uma parada inicial do teste.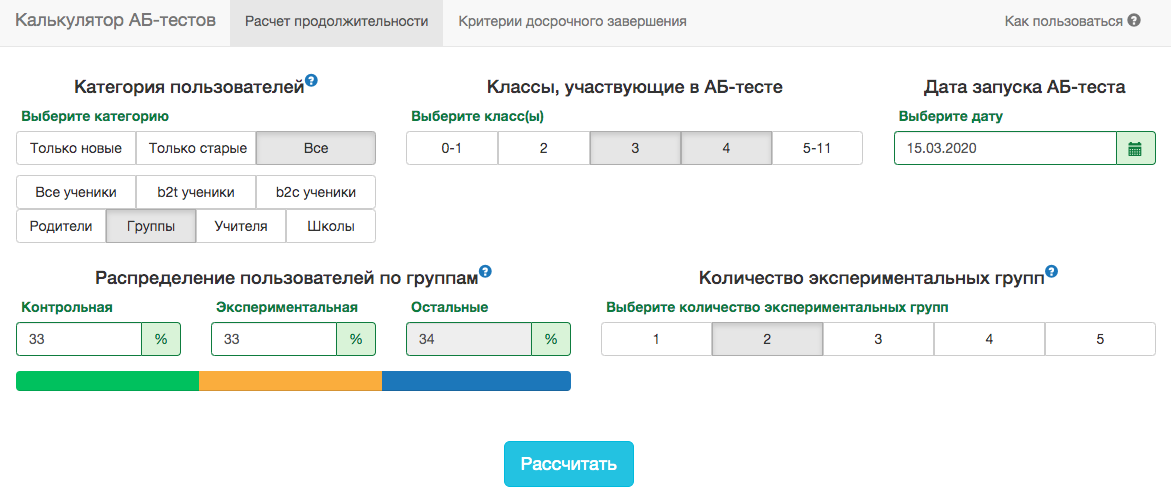

Todas as métricas são calculadas no nível dos objetos de teste. Se a métrica for o número de problemas resolvidos, na prova no nível do professor, essa será a soma dos problemas resolvidos pelos alunos. Como usamos o critério do aluno, podemos pré-calcular os agregados necessários à calculadora para todas as fatias possíveis. Para cada dia desde o início do teste, você precisa saber o número de pessoas no teste

u s e r s_c n t

$users\_cnt$ , o valor médio da métrica

m e t r i c_m e a n

$metric\_mean$ e sua variância

m e t r i c_s t d

$metric\_std$ . Corrigindo os compartilhamentos do grupo de controle

c o n t r o l_g r o u p_s h a r e

$control\_group\_share$ Grupo experimental

e x p_g r o u p_s h a r e

$exp\_group\_share$ e ganho esperado do teste

u p l i f t_e x p e c t e d

$uplift\_expected$ em porcentagem, você pode calcular os valores esperados das estatísticas dos alunos

t t e s t_s t a t_v a l u e

$ttest\_stat\_value$ e o valor p correspondente a cada dia do teste:

t t e s t_s t a t_p r e c u r s o r = \frac{m e t r i c_m e a n \sqrt{u s e r s_c n t}}{m e t r i c_s t d} t t e s t_s t a t_v a l u e = \frac{t t e s t_s t a t_p r e c u r s o r}{\sqrt{\frac{1}{c o n t r o l_g r o u p_s h a r e} + \frac{1}{e x p_g r o u p_s h a r e}}} * u p l i f t_e x p e c t e d / 100

$ttest\_stat\_precursor = \frac{metric\_mean\ \sqrt {users\_cnt}}{metric\_std} \\ ttest\_stat\_value = \frac {ttest\_stat\_precursor} {\sqrt{ \frac{1} {control\_group\_share} + \frac {1} {exp\_group\_share}}} * uplift\_expected / 100$

Em seguida, é fácil obter valores de p para cada dia:

pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2

Conhecendo o valor-p e o nível de significância, levando em consideração todas as correções de cada dia do teste, para qualquer duração do teste, é possível calcular a elevação mínima que pode ser detectada (na literatura inglesa - MDE, efeito detectável mínimo). Depois disso, é fácil resolver o problema inverso - determinar o número de dias necessários para identificar a elevação esperada.

Conclusão

Concluindo, quero lembrar as principais mensagens do artigo:

Se você comparar os valores médios da métrica em grupos, provavelmente, o critério Student será o mais adequado. A exceção são tamanhos de amostra extremamente pequenos (dezenas de observações) ou distribuições métricas anormais (na prática, eu não vi isso).
Se houver vários grupos no teste, use correções para o teste de múltiplas hipóteses. A correção mais simples de Bonferroni servirá.
.
. .
. , , , , O'Brien-Fleming.
A/B-, A/A-.

Apesar de tudo isso, negócios e bom senso não devem sofrer por uma questão de rigor matemático. Às vezes, é possível implementar o funcional para tudo o que não mostrou um aumento significativo no teste; algumas mudanças inevitavelmente ocorrem sem o teste. Mas se você realizar centenas de testes por ano, a análise precisa deles é especialmente importante. Caso contrário, existe o risco de o número de testes falso-positivos ser comparável aos testes realmente úteis.

A que prestamos atenção ao calcular a significância estatística do teste A / B