Lógica difusa e máquinas de estado contra o controlador PID. Vencer os bebês continua

Continuamos a estudar a lógica nebulosa de acordo com o livro de V. Gostev, "Controladores nebulosos em sistemas de controle automático". Depois de apreciar as belas vistas das superfícies de resposta , prosseguimos diretamente para resolver o próximo problema do livro de V. Gostev "Controladores difusos em sistemas de controle automático".

Este texto é uma continuação de publicações anteriores:

1. Um controlador simples baseado em lógica difusa. Criação e customização.
2. Lógica confusa em belas fotos. Superfícies de resposta para diferentes funções de associação.
3. Criando um controlador baseado em lógica nebulosa com configurações multicanais.
4. A lógica difusa simples é moldada “a partir do que era” para um motor de turbina a gás.
5. Lógica difusa contra PID. Atravessamos o ouriço e a cobra. Motor de aeronave e algoritmos de controle da NPP.

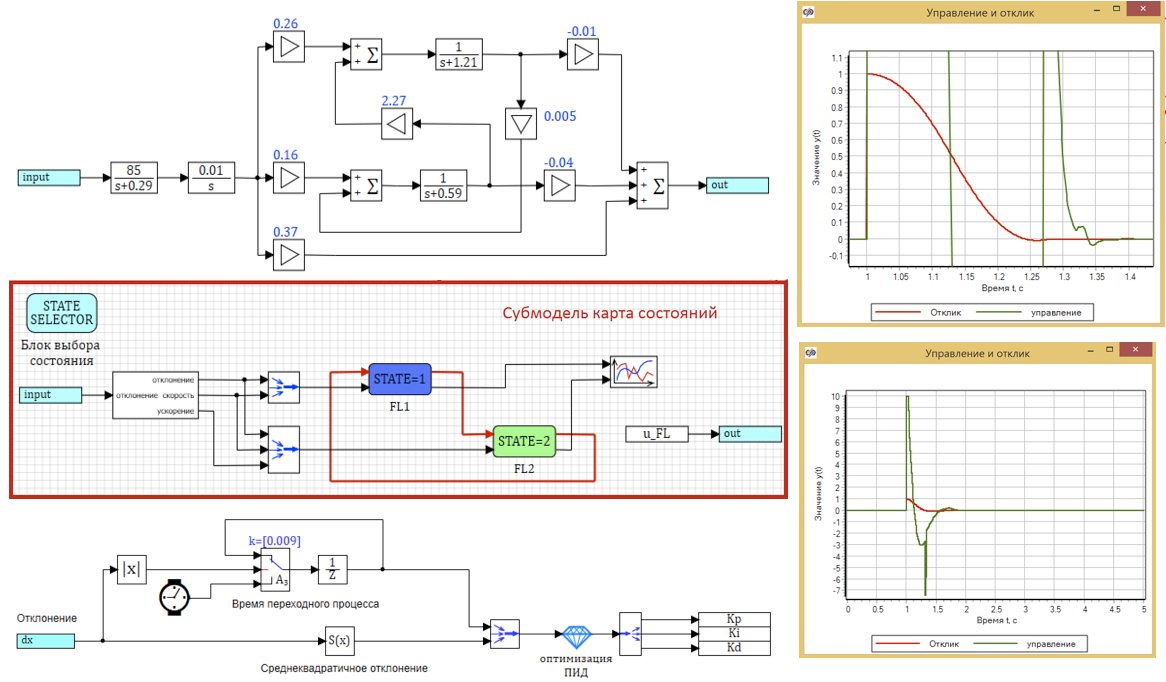
Para aqueles que não estão familiarizados com a lógica difusa, recomendo que você leia primeiro o primeiro texto; depois disso, tudo o que é descrito abaixo será simples e claro.

, - . , . , Fuzzy. , , . , , , , .

, , , .

– -, (). , , « . »

, , , 1 ( ).

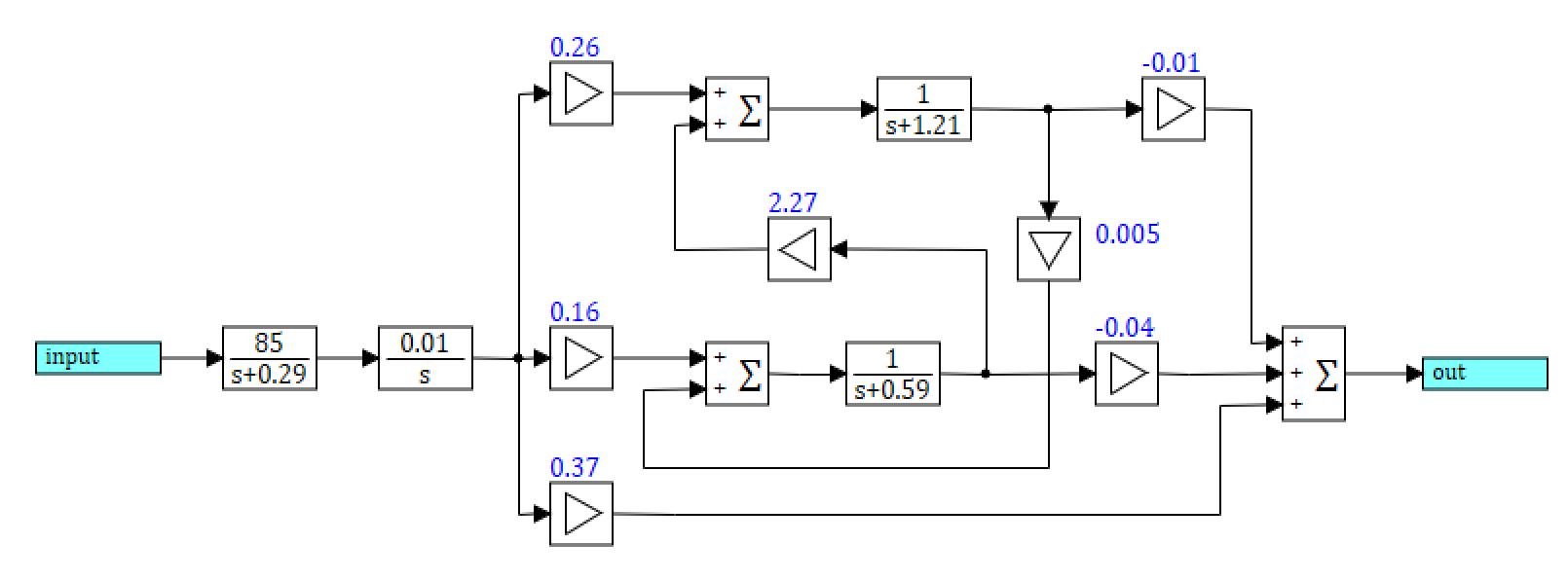
1. .

.
. 1 . , . – , .

: – , – . , 0.009 .

, -.

, 2. – 20, (- «as is» .. ).

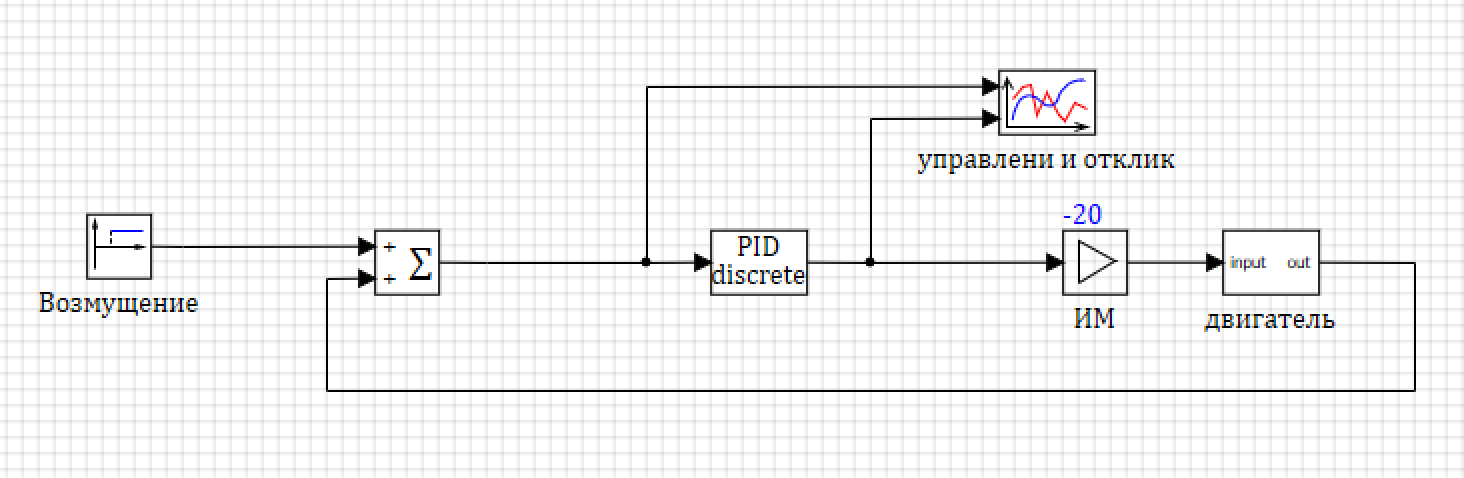
2. .

- 0.001 0.001.

- 1,1,1 . 3.

, , 1 1000, 0,001. , . , -1 1 , 0 7 .

O que você pode dizer olhando para este gráfico? Deixa pra lá. E tudo porque nosso modelo já é apresentado como uma função de transferência em desvios, e não podemos dizer se é rápido ou não. Não podemos dizer nada sobre o mecanismo. Como já mostrei no artigo “Tecnologia para obtenção de equações dinâmicas de TAU. E por que a Identificação do sistema é péssima e a “física honesta” governa : a transformação de um sistema físico paramétrico em um tipo de função de transferência arruina toda a “compreensibilidade” de engenharia do modelo.
Por exemplo, o impacto em um modelo com um valor de 1000 obtido após o PID é possível na vida? Desconhecido Se este for um suprimento de combustível, é óbvio que o sistema de suprimento não poderá fornecer 1000 vezes mais combustível do que no modo ocioso.

, 10, -10. . , . :

4. .

, , ( 5). 1000, , 10.

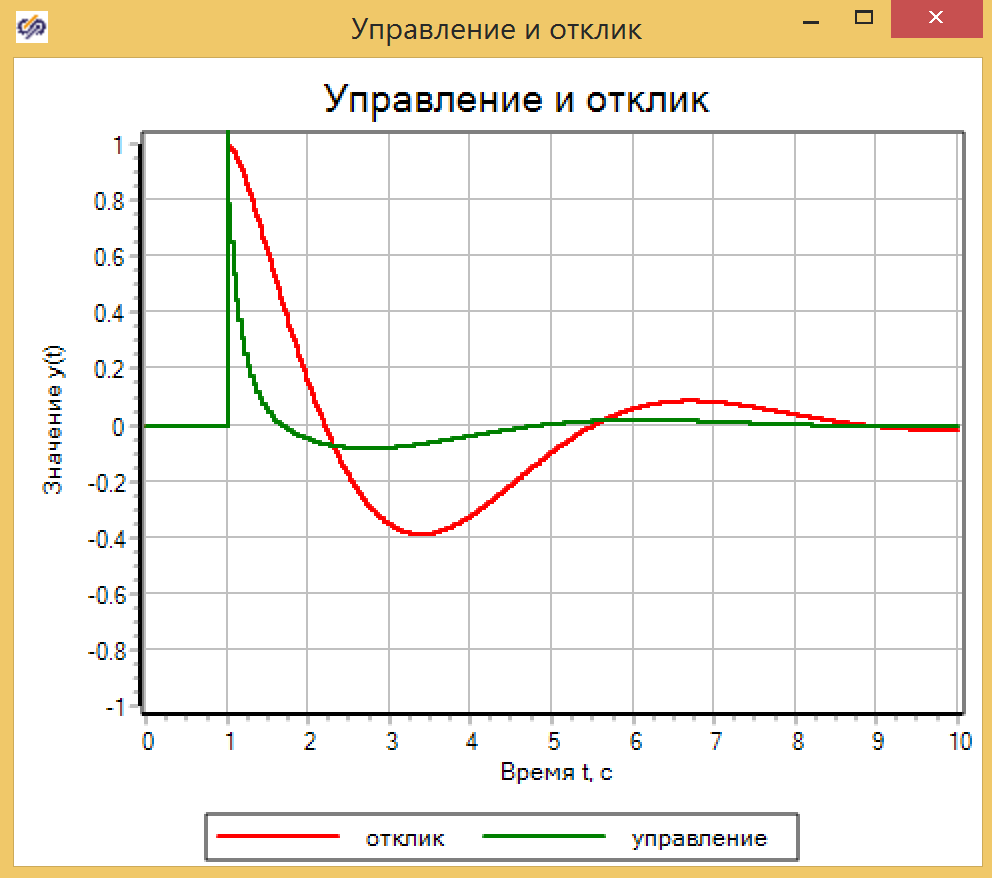
5. .

.
C . 0

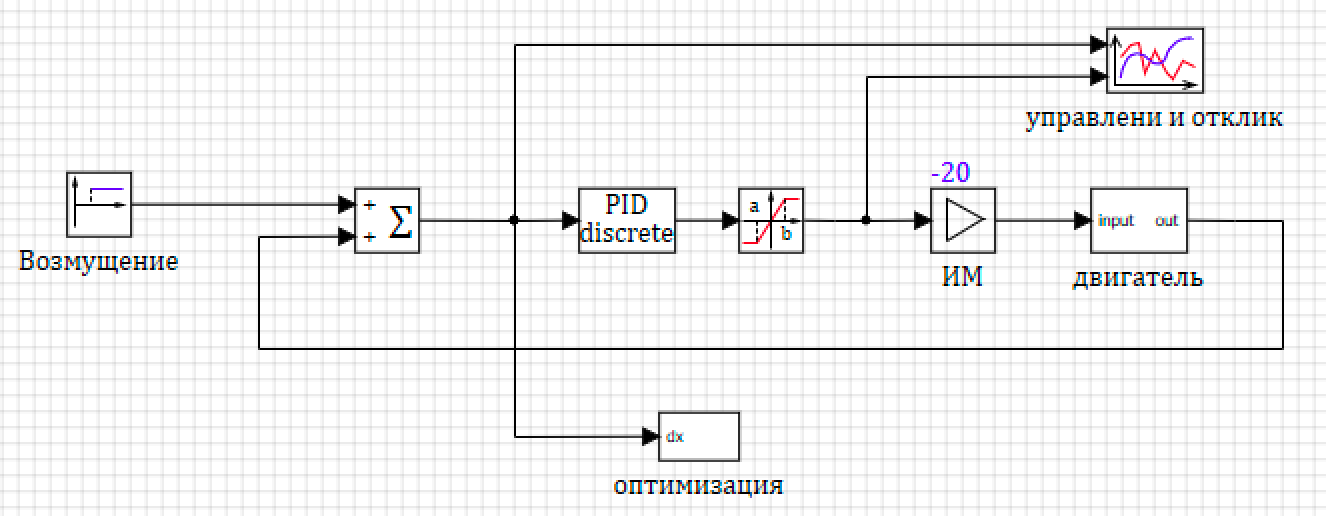
6. .

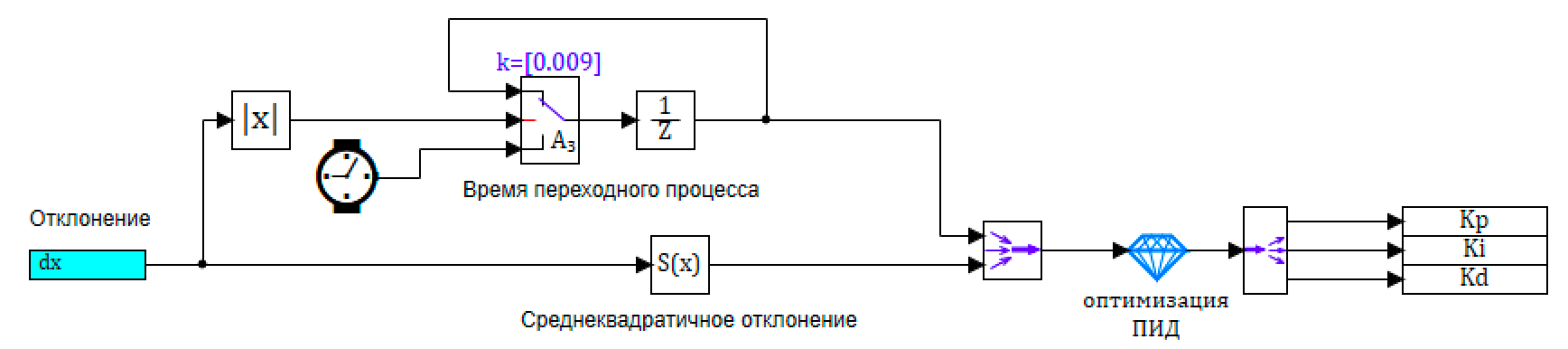7.

7. ..

. :
— – , 0.009.
— .

«-3» . , , , — .

« » .

, , . , .

, « » , , .. .

, , . , .
, . , , , .

8.

8. .

. , , . p, Ki, Kd (. . 7 . 8). -. (. 10.)

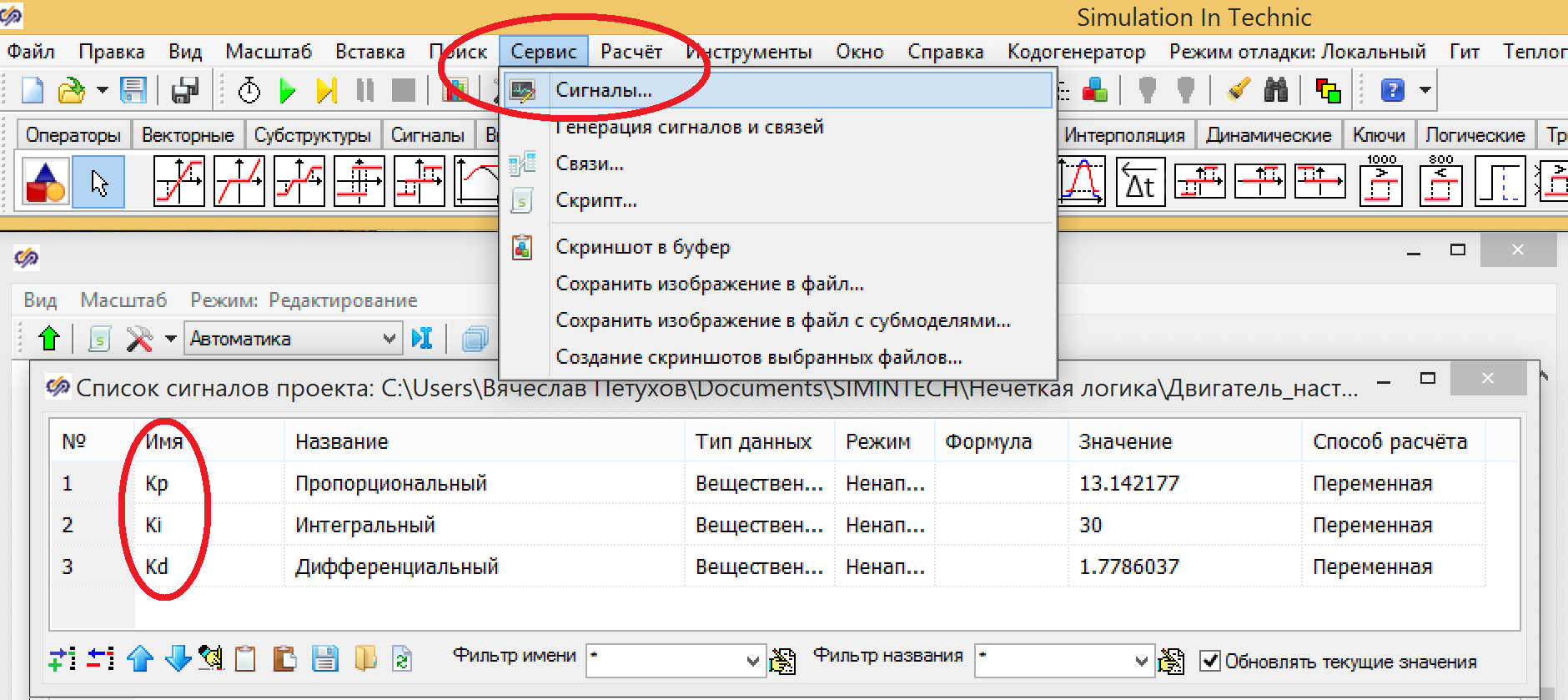
9. .

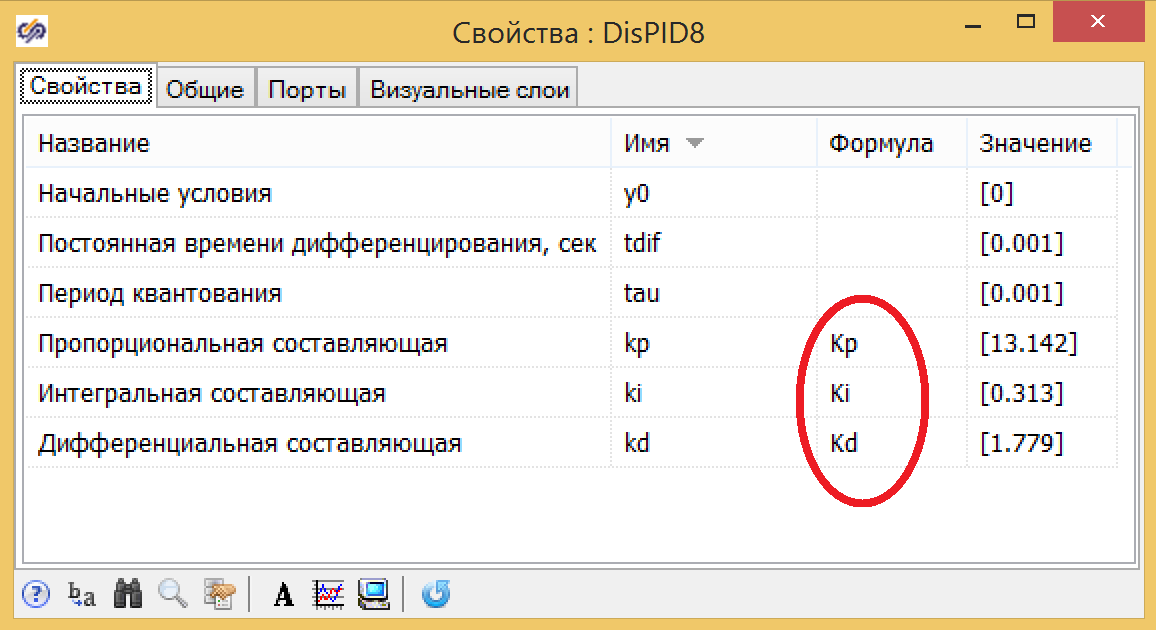
10. -.

:
Kp = 13.142
Ki = 0.313
Kd = 1.779
0.72 . 11.

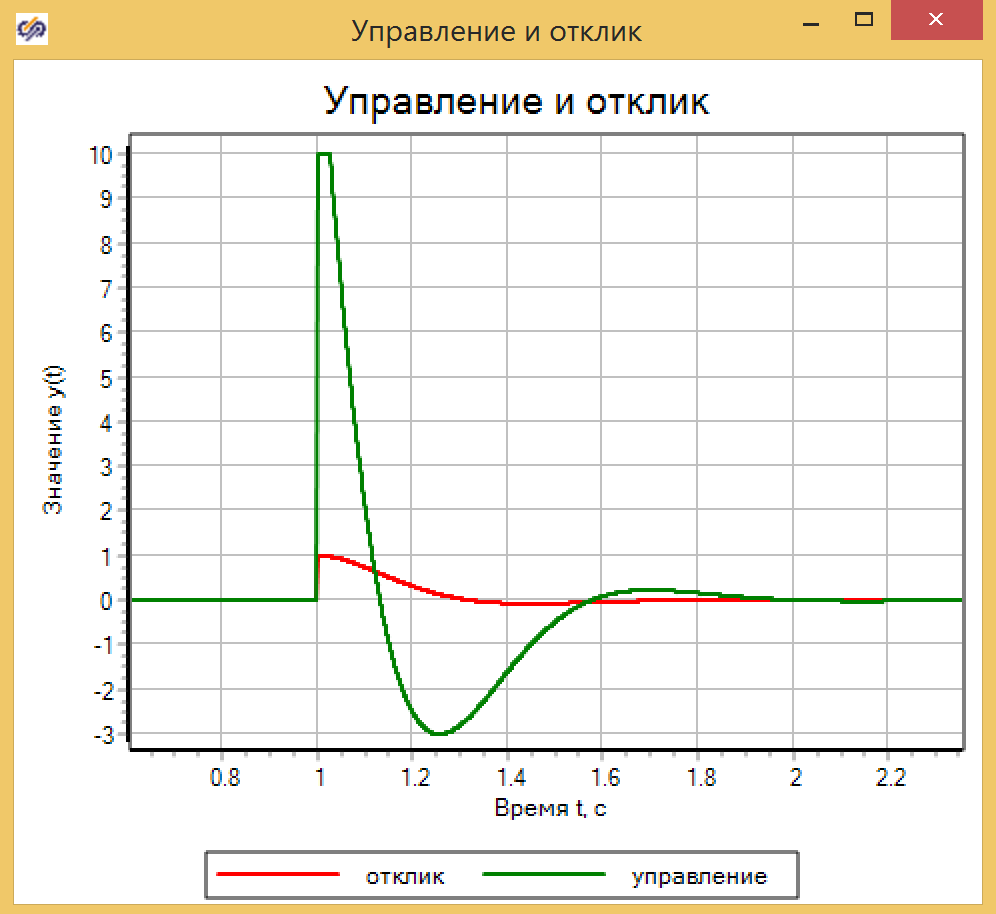
11. -.

, .

1 , . .

Os sinais de desvio recebidos e a taxa de variação do desvio, passando pelas unidades de fase, são decompostos em três termos cada. Usando as funções de associação do Gauss.

Desvio - mais , norma , menos .
A taxa de mudança está crescendo , não está mudando , está caindo .

O regulador produzirá um efeito quando um desvio aparecer, bem como quando a taxa de variação do regulador indicar que o desvio aumentará (mesmo que no momento seja normal). Regras básicas para o regulador:

1. ( (0) ), .
2. , 0.
3. ( (0) ), .

, , 12.

12. Fuzzy Logic.

. , 0, . :

• uMax_1 – ;
• deltaMax_1 – ;
• divMax_1 – .

– . 13.

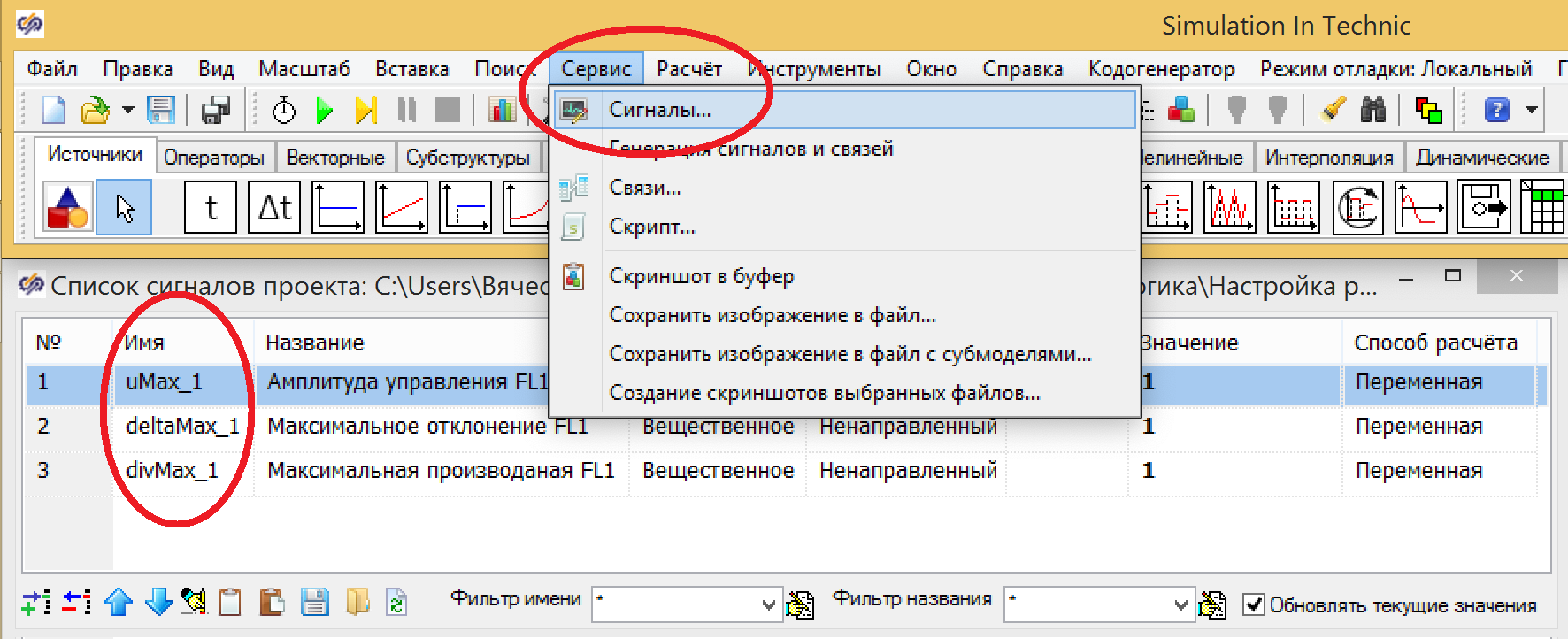
13. .

(–uMax_1… uMax_1) [–uMax_1 ,0, uMax_1], , 2. (. , ).

, :

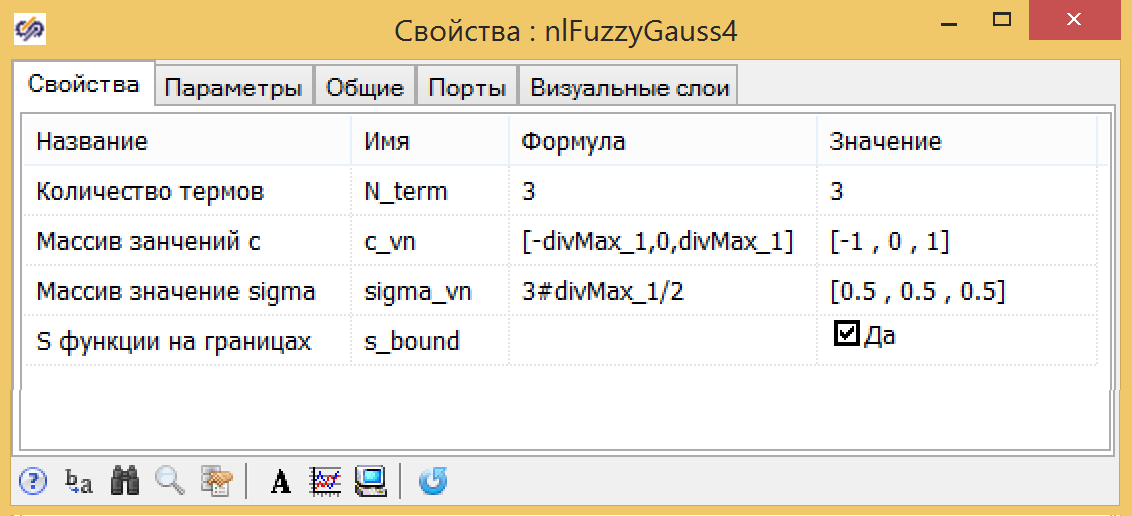14. .

.
, :

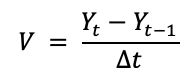onde:
Y _t é o valor atual;
Y _t-1 é o valor na etapa anterior;
Δt = 0,001 - o intervalo de tempo é o mesmo que na amostragem de um controlador PID discreto.

O circuito é mostrado na Figura 15. A divisão por Δt é levada em consideração no bloco de comparação, onde os coeficientes para cada entrada podem ser definidos.

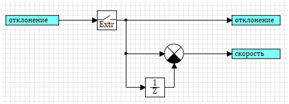
Figura 16. Esquema para calcular a taxa de mudança.

Como todo o circuito está pronto para nós, resta substituir o controlador PID pelo controlador FL (veja a Figura 17) e veja o que acontece.

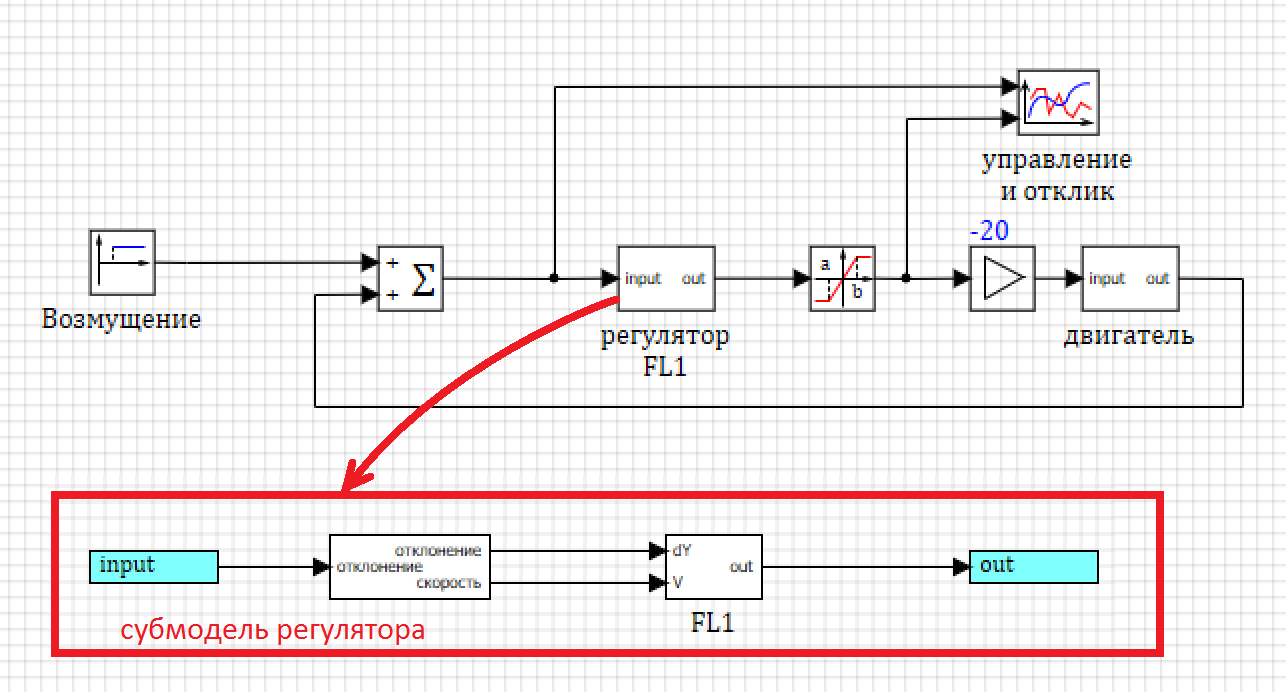
Figura 17. Diagrama de um modelo com um controlador difuso.

E, novamente, para minha surpresa considerável, o controlador difuso se saiu melhor que o PID nas configurações únicas iniciais. É obtido algum tipo de publicidade contínua da lógica difusa.

Além disso, se em casos anteriores isso poderia ser atribuído ao fato de que a segunda derivada é usada no controlador nebuloso, nesse caso, esse controlador nebuloso usa a mesma derivada e o PID também usa o componente integral.

Para que os defensores da diversidade de gênero não me acusem de oprimir os controladores PID tradicionais, o coeficiente do componente integral é anulado e um controlador PD é obtido. O resultado melhorou significativamente, mas o FL ainda é melhor.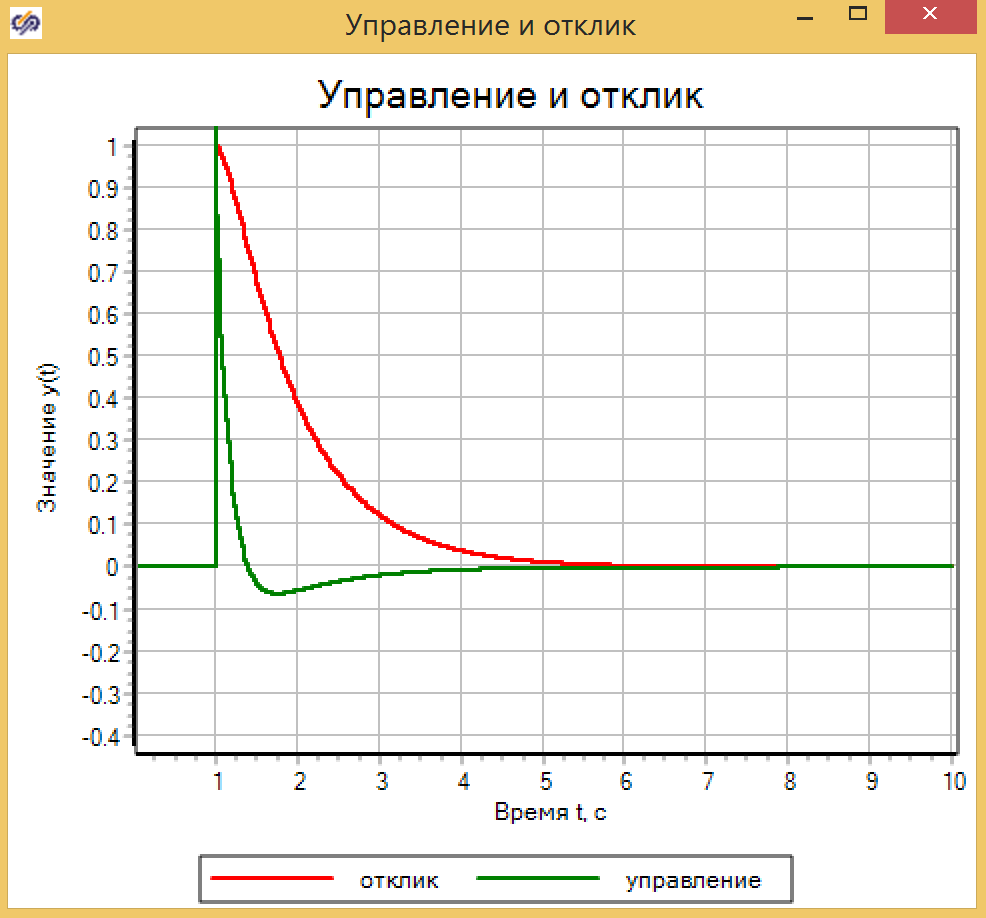

Figura 19. Controlador PD com configurações únicas.

, 0.009. :
– 11.25 .
— 5.25 .
FL – 4.74 .

FL

, - (. 6). :
— uMax_1 – ;
— deltaMax_1 – ;
— divMax_1 – .

1. .

, .

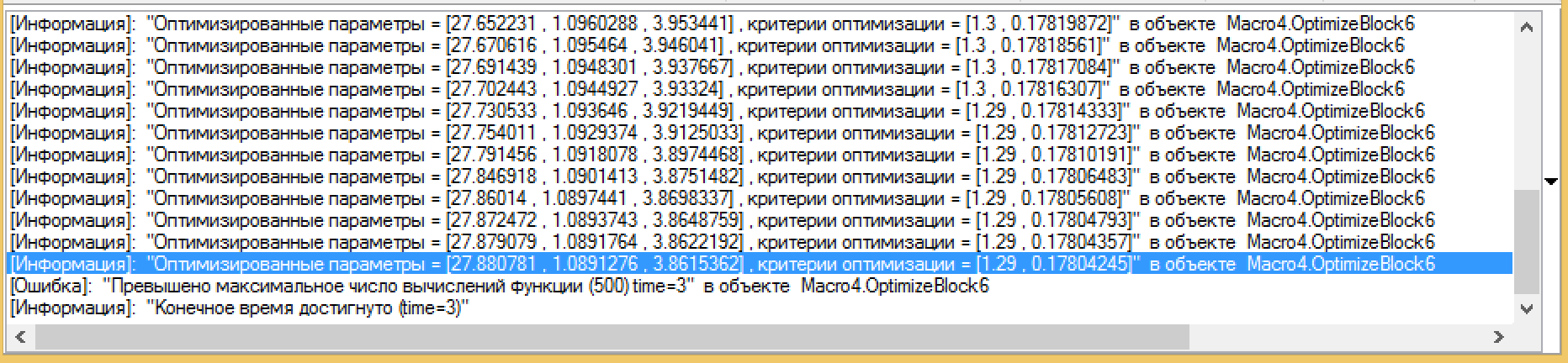
20. .

, , .

. .

21. .

0.24
[]: « = [31.10359, 1.0219553, 2.165446], = [1.24, 0.09879439]» Macro4.OptimizeBlock6

0.23 .
[]: « = [34.954824, 1.0114662, 0.058949452], = [1.23, 0.098544697]» Macro4.OptimizeBlock6

FL 22. , .

, .

, . . , , , .

, , , .

. – SimInTech, - , .

. . – FL1, — FL2. , 23:

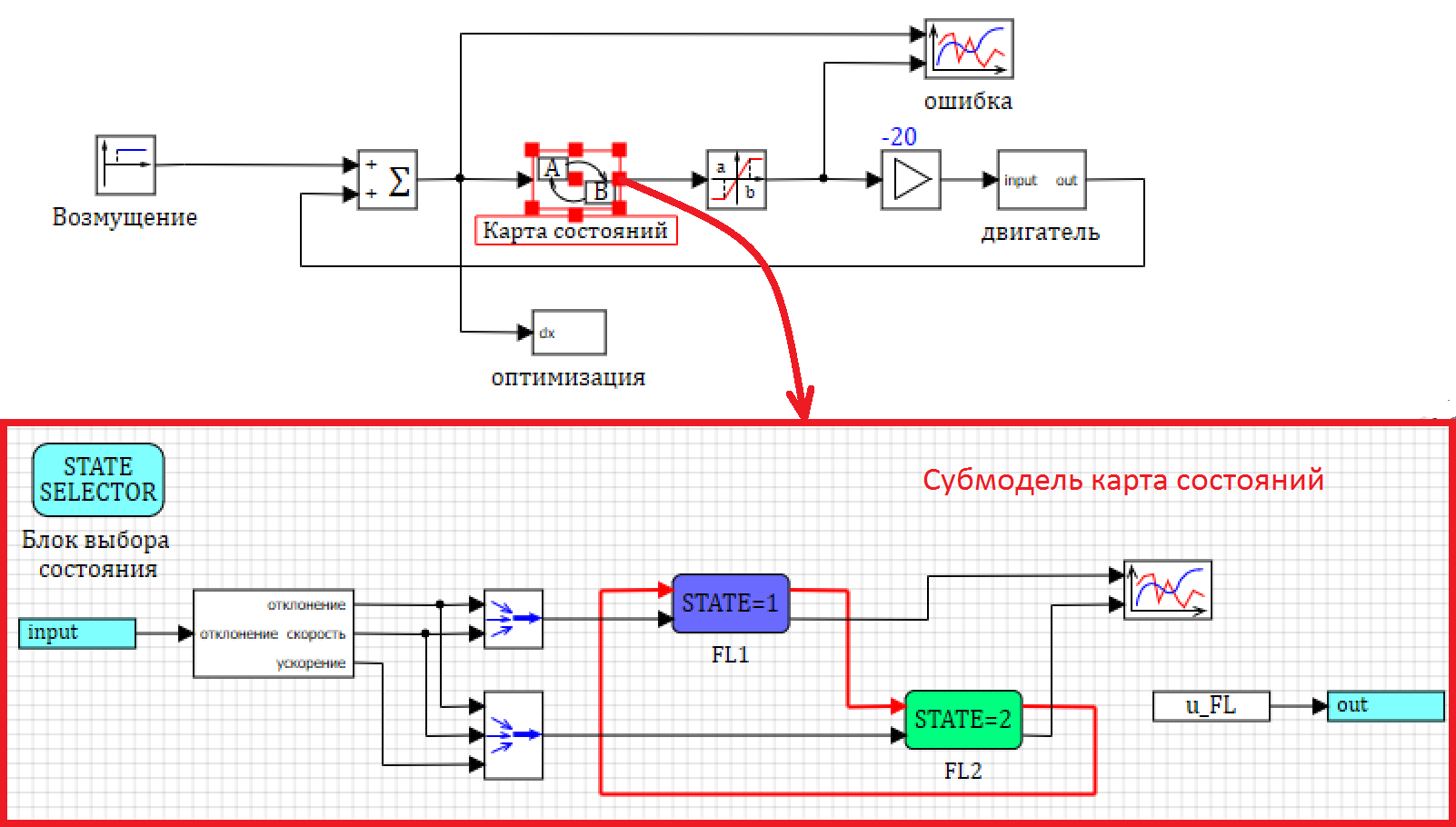
23. .

, , – , .

, .

, , , , . .

, , , «1 », , 0.001 ( ). . — .

, , , (), . , , 1000 , 1 000 000 . . . 24.

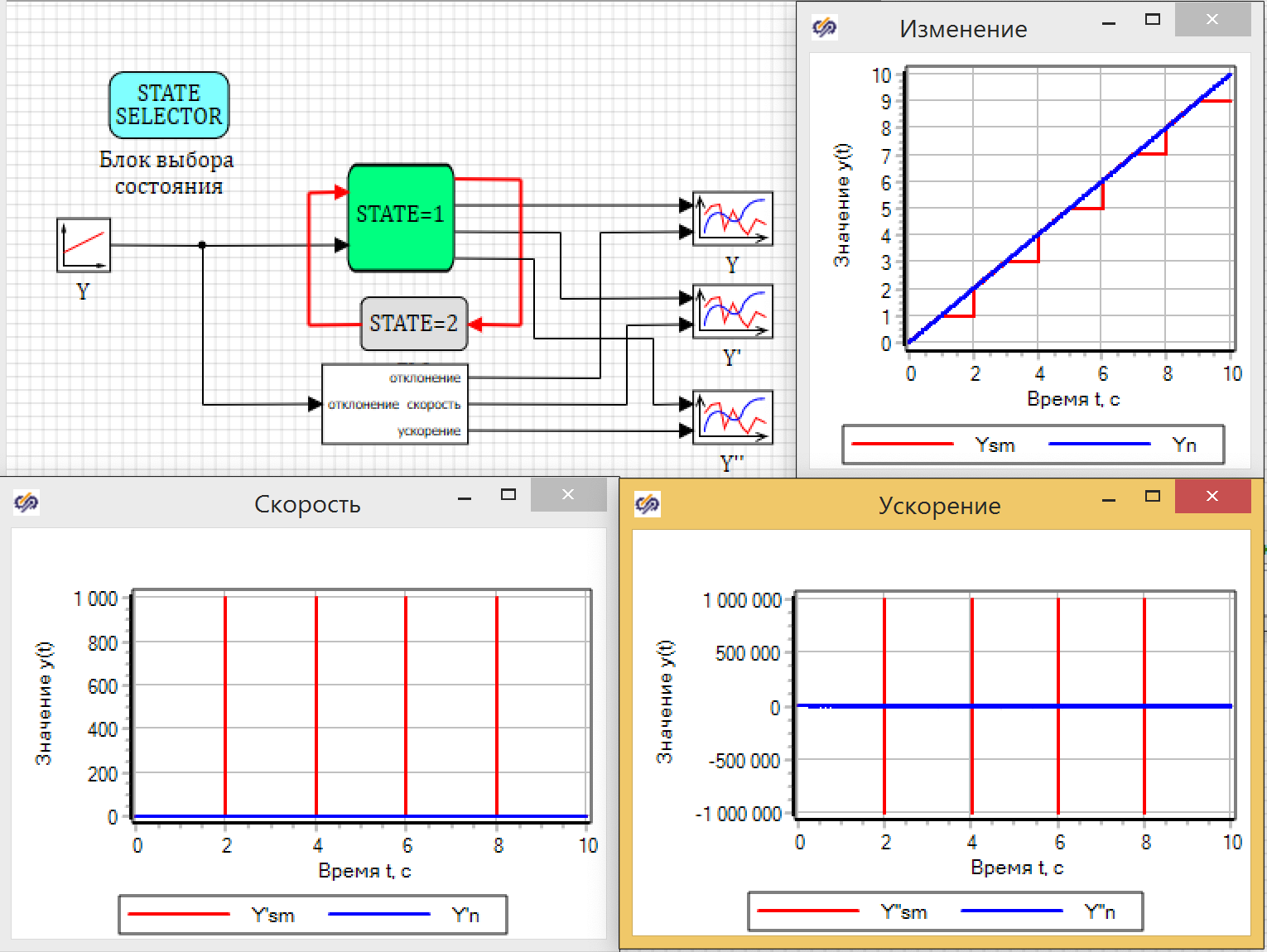
24. .

: , 0.009. , , .

FL1, . , u_FL. , , .

25. 1.

– , 1 , 0.009.

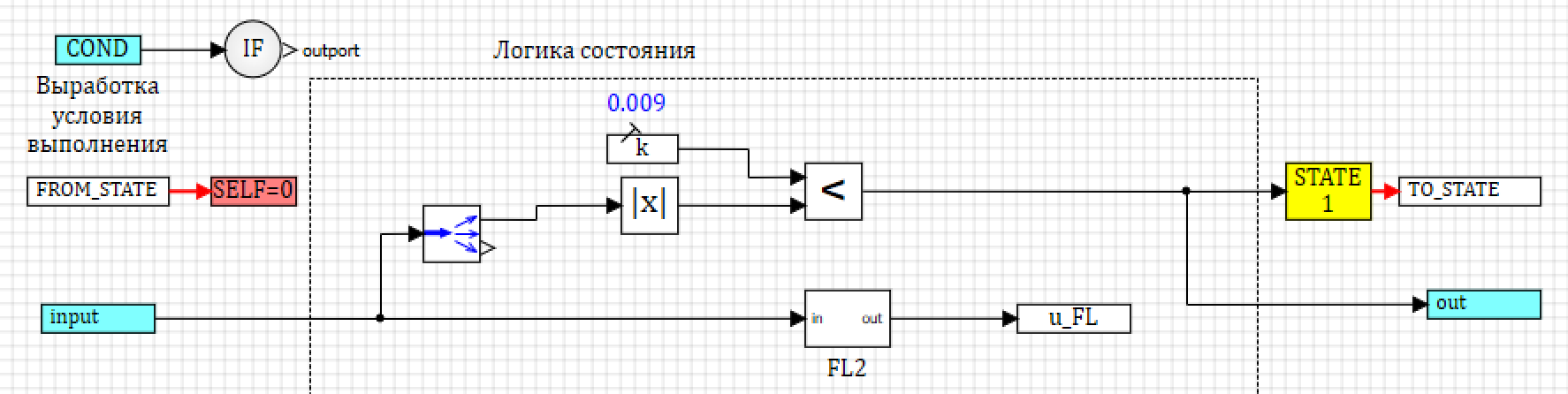26. 2.

( .. ). 24.

, , u_FL FL1, FL2 .

. , . , . , , .

– , , .
– , , .
— , , .

, :

1) se o desvio for maior e a taxa de mudança aumentar e a aceleração da mudança acelerar , o efeito será reduzido .
2) se o desvio é normal e a taxa de mudança é constante e a aceleração da mudança não muda , o efeito não muda .
3) se o desvio for menor e a taxa de mudança diminuir e a aceleração da mudança diminuir , então aumento de impacto .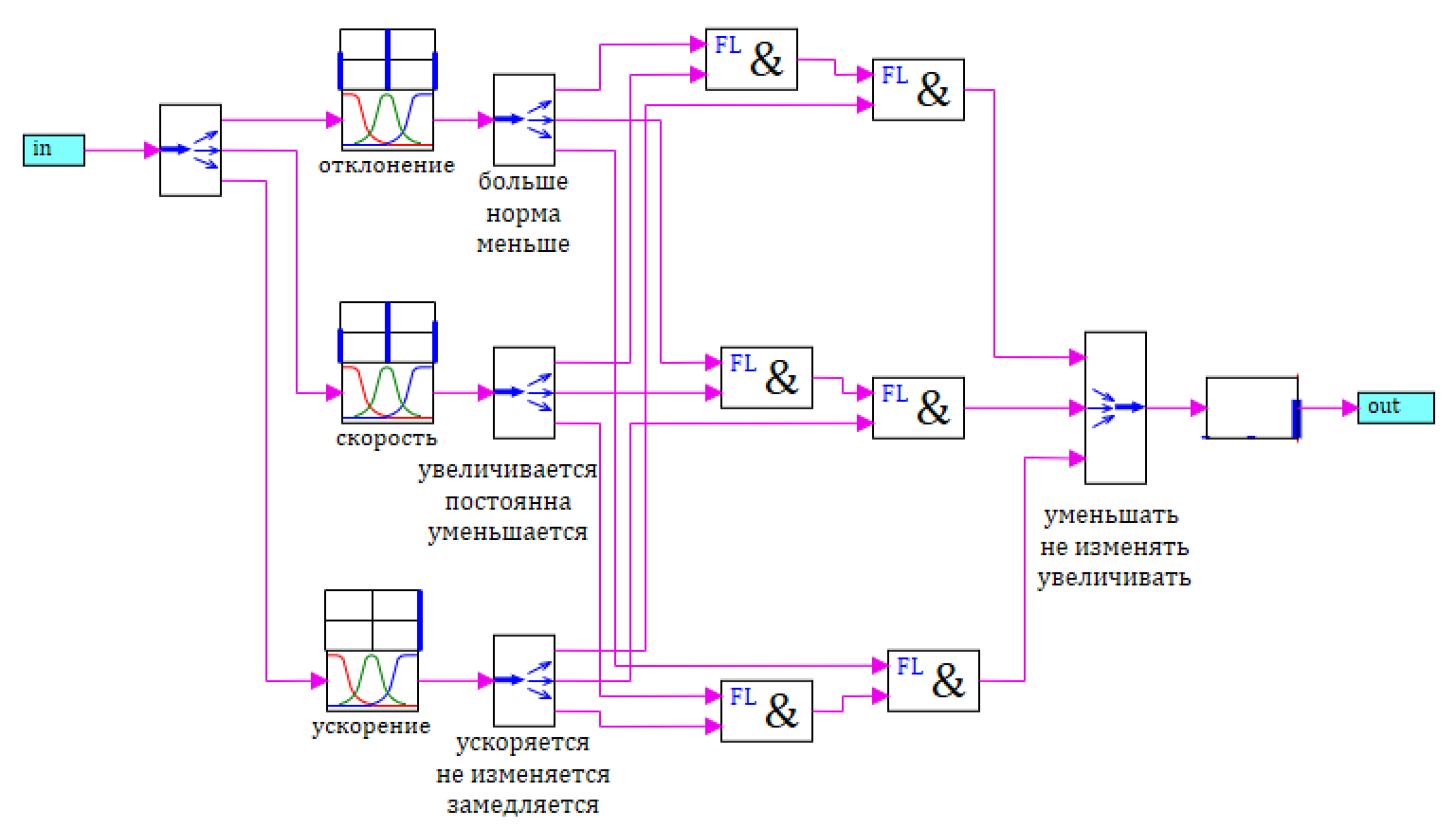

27. FL2.

N , , 0, .
:
— uMax_2 – ;
— deltaMax_2 – ;
— divMax_2 – ;
— div2Max_2 – .

1 (. . 28)
1 , - , , 1 (. . 18 — 19) – , . . (. . 28)

28. .

: , . 29, – 30.

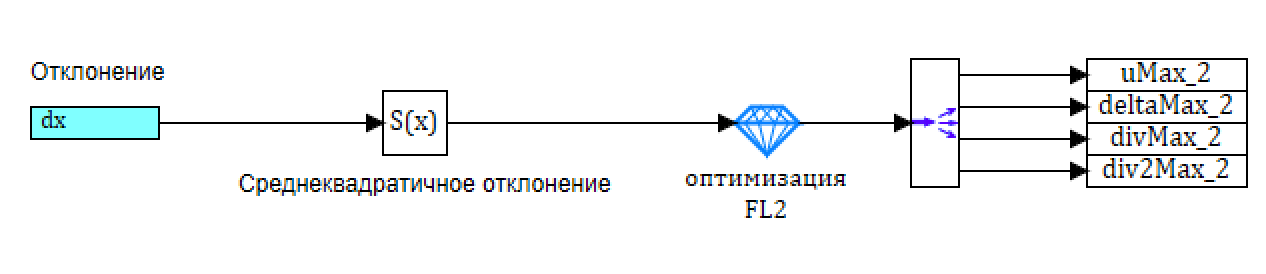
29. .

30. .

, . , . , .

, . .
:
sign, -1,0,1 , « », 1 . , , .
, .

, , 1.2 , .

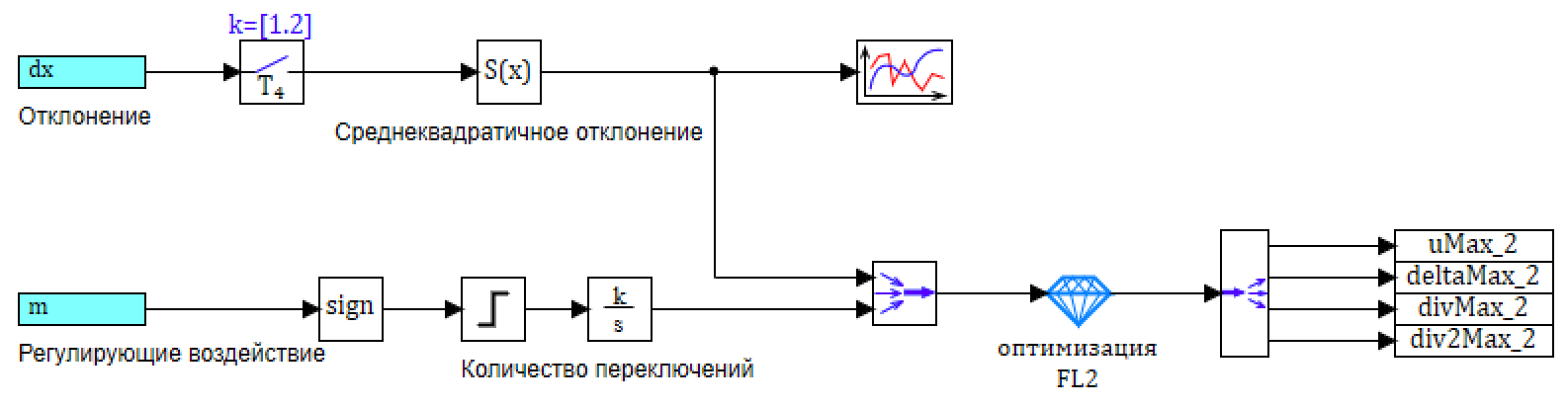
31. ee.

:

[]: « = [16.564415, 0.0027674129, 0.19085771, 50], = [0.0047956855, 11]» Macro5.OptimizeBlock6

, :
— uMax_2 – = 16.564;
— deltaMax_2 – = 0.00277;
— divMax_2 – = 0.191;
— div2Max_2 – = 50.
32.

, , , . 1, 2 , .

33. , , .

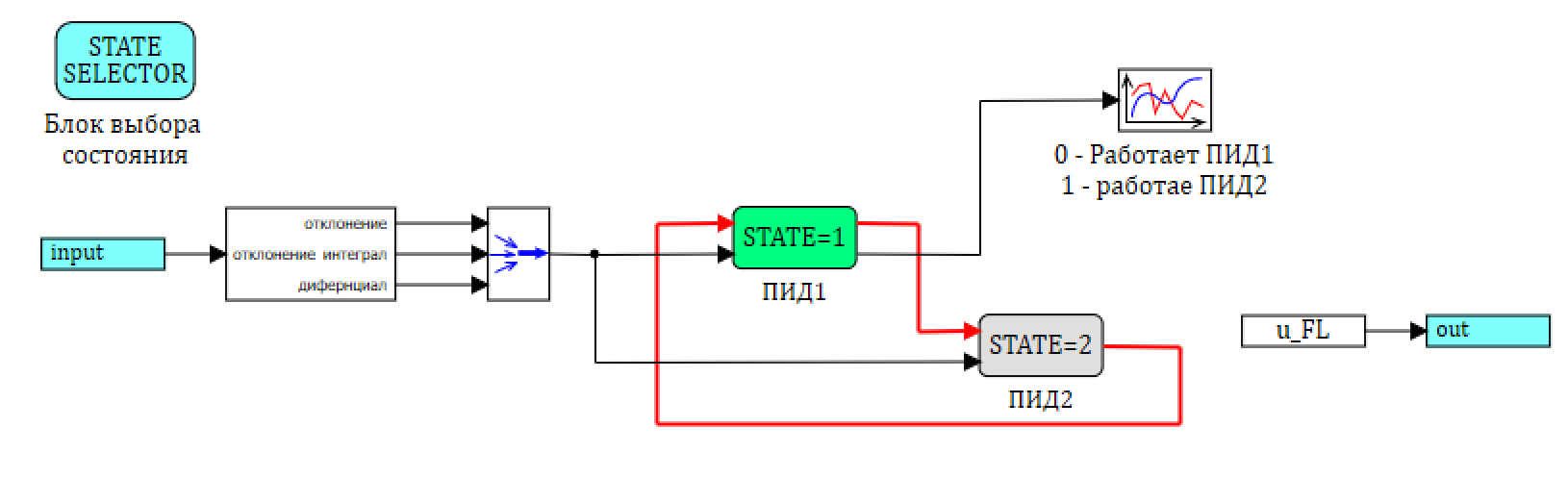33. 1 2.

, , , . . 34.

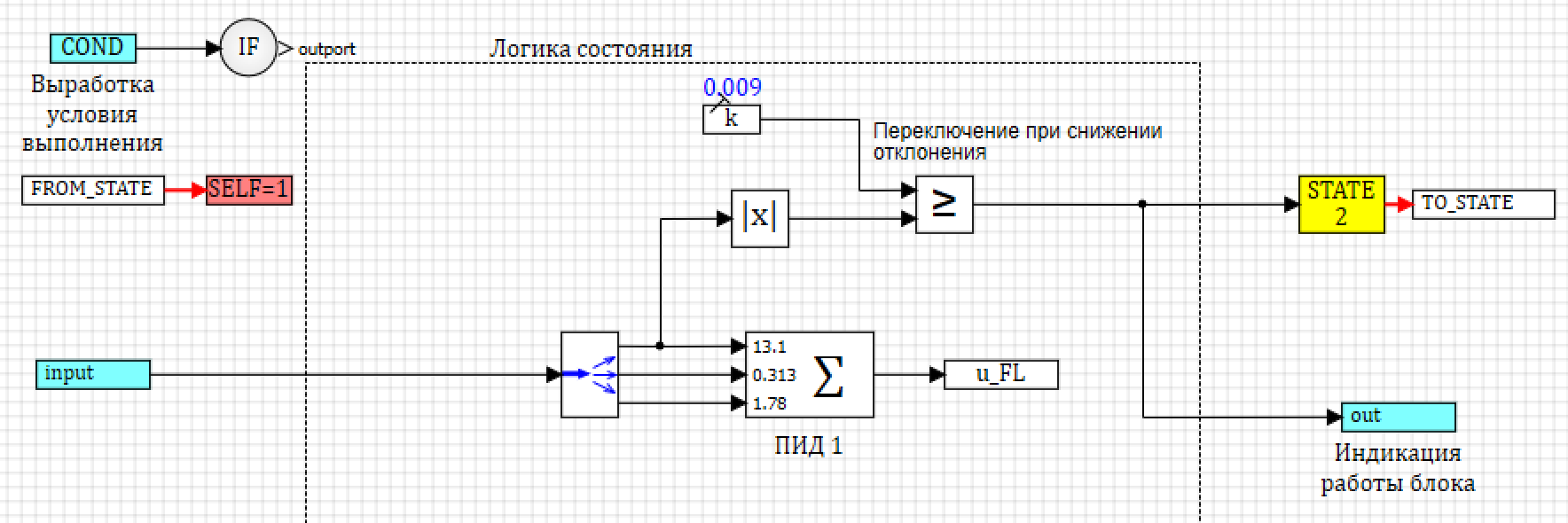
34. -.

2, , . - :

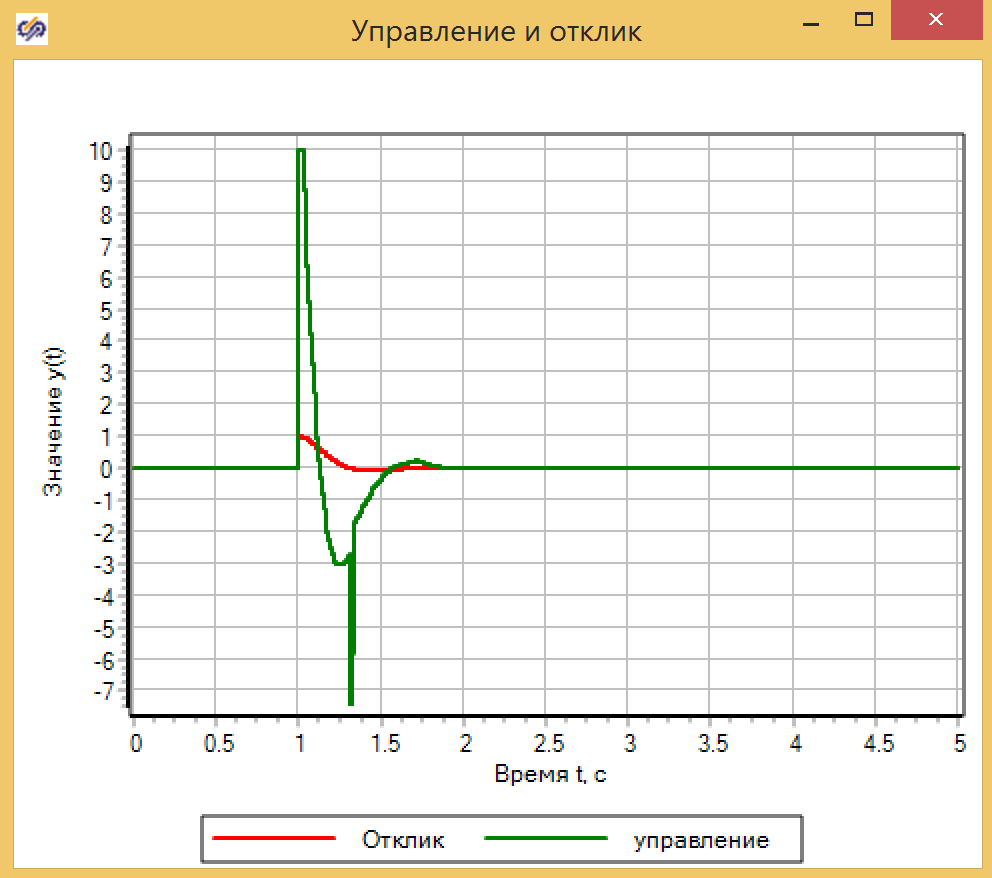
35. -.

:

, , .

...