Na parte anterior, descobrimos como exibir objetos bidimensionais, como um pixel e uma linha (segmento), mas você realmente deseja criar rapidamente algo tridimensional. Neste artigo, pela primeira vez, tentaremos exibir um objeto 3D na tela e nos familiarizar com novos objetos matemáticos, como um vetor e uma matriz, além de algumas operações sobre eles, mas apenas aqueles que são aplicáveis na prática.Na segunda parte, consideraremos:- Sistemas coordenados
- Ponto e vetor
- O Matrix
- Vértices e índices
- Transportador de visualização
Sistemas coordenados
Vale ressaltar que alguns exemplos e operações nos artigos são apresentados de maneira imprecisa e bastante simplificada para melhorar a compreensão do material, compreendendo a essência, você pode encontrar independentemente a melhor solução ou corrigir erros e imprecisões no código de demonstração. Antes de desenharmos algo tridimensional, é importante lembrar que todas as tridimensionais na tela são exibidas em pixels bidimensionais. Para que os objetos desenhados por pixels pareçam tridimensionais, precisamos fazer um pouco de matemática. Não consideraremos fórmulas e objetos sem ver sua aplicação. É por isso que todas as operações matemáticas que você encontrará neste artigo serão colocadas em prática, o que simplificará sua compreensão. A primeira coisa a entender é o sistema de coordenadas. Vamos ver quais sistemas de coordenadas são usados e também escolher qual deles usar para nós.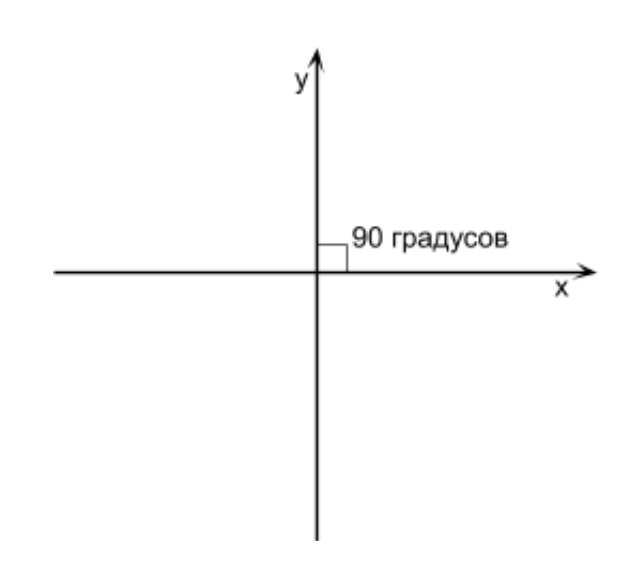
O que é um sistema de coordenadas? Essa é uma maneira de determinar a posição de um ponto ou personagem em um jogo que consiste em pontos usando números. O sistema de coordenadas possui 2 direções dos eixos (nós os designaremos como X, Y) se trabalharmos com gráficos 2D. Se definirmos um objeto 2D com um Y maior e ele se tornar maior do que era antes, isso significa que o eixo Y está para cima. Se atribuirmos ao objeto um X maior e ele se tornar mais à direita, isso significa que o eixo X é direcionado para a direita. Essa é a direção dos eixos e juntos eles são chamados de sistema de coordenadas. Se um ângulo de 90 graus é formado na interseção dos eixos X e Y, esse sistema de coordenadas é chamado de retangular (também chamado de sistema de coordenadas cartesianas) (veja a figura acima).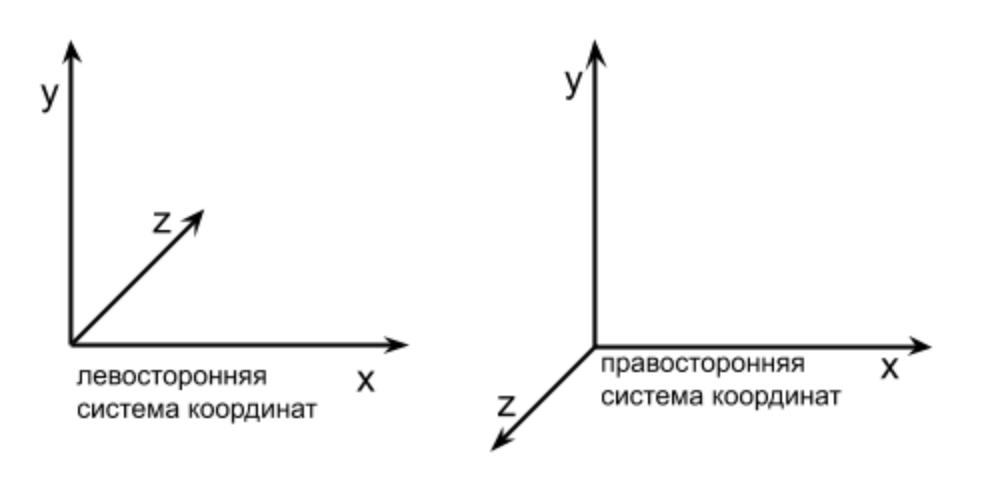
Ponto e vetor
Agora você basicamente sabe o que são sistemas de coordenadas e quais são as direções dos eixos. Em seguida, você precisa analisar o que é um ponto e um vetor, porque precisaremos deles neste artigo para praticar. Um ponto no espaço 3D é um local especificado através de [X, Y, Z]. Por exemplo, queremos colocar nosso personagem na própria origem (talvez no centro da janela), então sua posição será [0, 0, 0], ou podemos dizer que ele está localizado no ponto [0, 0, 0]. Agora, queremos colocar o oponente à esquerda das 20 unidades do jogador (por exemplo, pixels), o que significa que ele estará localizado no ponto [-20, 0, 0]. Trabalharemos constantemente com pontos, para analisá-los com mais detalhes posteriormente. O que é um vetor? Essa é a direção. No espaço 3D, é descrito, como um ponto, por 3 valores [X, Y, Z]. Por exemplo, precisamos mover o personagem para cima 5 unidades a cada segundo, para mudar Y, adicionando 5 a cada segundo, mas não tocaremos em X e Z, esse movimento pode ser escrito como um vetor [0, 5, 0]. Se nosso personagem se move constantemente para baixo em 2 unidades e para a direita em 1, então o vetor de seu movimento ficará assim: [1, -2, 0]. Nós escrevemos -2 porque Y para baixo diminui.O vetor não tem posição e [X, Y, Z] indica a direção. Um vetor pode ser adicionado a um ponto para que um novo ponto seja deslocado por um vetor. Por exemplo, eu já mencionei acima que, se quisermos mover um objeto 3D (por exemplo, um personagem do jogo) a cada 5 unidades, o vetor de deslocamento será assim: [0, 5, 0]. Mas como usá-lo para mover? Suponha que o caractere esteja no ponto [5, 7, 0] e o vetor de deslocamento seja [0, 5, 0]. Se adicionarmos um vetor ao ponto, obteremos uma nova posição de jogador. Você pode adicionar um ponto com um vetor ou um vetor com um vetor de acordo com a regra a seguir.Um exemplo de adição de um ponto e um vetor :[ 5, 7, 0 ] + [ 0, 5, 0 ] = [ 5 + 0, 7 + 5 , 0 + 0 ] = [5, 12, 0] - esta é a nova posição do nosso personagem. Como você pode ver, nosso personagem subiu 5 unidades para cima, a partir daqui um novo conceito aparece - o comprimento do vetor. Cada vetor possui, exceto o vetor [0, 0, 0], que é chamado de vetor zero; esse vetor também não tem direção. Para o vetor [0, 5, 0], o comprimento é 5, porque esse vetor desloca o ponto 5 para cima. O vetor [0, 0, 10] tem um comprimento de 10 porque ele pode mudar o ponto em 10 ao longo do eixo Z. Mas o vetor [12, 3, -4] não informa qual é o comprimento, então usaremos a fórmula para calcular o comprimento do vetor. Surge a pergunta: por que precisamos do comprimento do vetor? Uma aplicação é descobrir até que ponto o personagem se moverá ou comparar a velocidade de caracteres com um vetor de deslocamento maior, que é mais rápido. O comprimento também é usado para algumas operações em vetores.O comprimento do vetor pode ser calculado usando a seguinte fórmula da primeira parte (somente Z foi adicionado):
Vamos calcular o comprimento do vetor usando a fórmula acima [6, 3, -8];
O comprimento do vetor [6, 3, -8] é de aproximadamente 10,44.Já sabemos o que é um ponto, um vetor, como somar um ponto e um vetor (ou 2 vetores) e como calcular o comprimento de um vetor. Vamos adicionar uma classe vetorial e implementar a soma e o cálculo do comprimento nela. Também quero prestar atenção ao fato de que não criaremos uma classe para um ponto, se precisarmos de um ponto, usaremos a classe vetorial, porque o ponto e o vetor armazenam X, Y, Z, apenas para o ponto nesta posição e para o vetor a direção.Adicione a classe vetorial ao projeto do artigo anterior; você pode adicioná-la abaixo da classe Drawer. Chamei Vector de minha classe e adicionei 3 propriedades X, Y, Z:class Vector {
x = 0;
y = 0;
z = 0;
constructor(x, y, z) {
this.x = x;
this.y = y;
this.z = z;
}
}
Observe que os campos x, y, z sem as funções de "acessadores", para que possamos acessar diretamente os dados no objeto, isso é feito para um acesso mais rápido. Mais tarde, otimizaremos ainda mais esse código, mas, por enquanto, deixe-o para melhorar a legibilidade.Agora, implementamos a soma dos vetores. A função terá dois vetores somados, então estou pensando em torná-la estática. O corpo da função funcionará de acordo com a fórmula acima. O resultado do nosso somatório é um novo vetor, com o qual retornaremos:static add(v1, v2) {
return new Vector(
v1.x + v2.x,
v1.y + v2.y,
v1.z + v2.z,
);
}
Resta implementar a função de calcular o comprimento do vetor. Novamente, implementamos tudo de acordo com as fórmulas mais altas:getLength() {
return Math.sqrt(
this.x * this.x + this.y * this.y + this.z * this.z
);
}
Agora, vejamos outra operação no vetor, que será necessária um pouco mais adiante neste e em muitos artigos subsequentes - "normalização do vetor". Suponha que tenhamos um personagem no jogo para quem nos movemos com as setas. Se pressionarmos para cima, ele se moverá para o vetor [0, 1, 0], se estiver para baixo, então [0, -1, 0], para a esquerda [-1, 0, 0] e para a direita [1, 0, 0]. Pode-se ver claramente aqui que os comprimentos de cada um dos vetores são 1, ou seja, a velocidade do personagem é 1. E vamos adicionar um movimento diagonal, se o jogador apertar a seta para cima e para a direita, qual será o vetor de deslocamento? A opção mais óbvia é o vetor [1, 1, 0]. Mas se calcularmos seu comprimento, veremos que ele é aproximadamente igual a 1,414. Acontece que nosso personagem vai mais rápido na diagonal? Essa opção não é adequada, mas, para que nosso personagem vá na diagonal na velocidade de 1, o vetor deve ser:[0,707, 0,707, 0]. Onde consegui esse vetor? Peguei o vetor [1, 1, 0] e o normalizei, após o qual obtive [0,707, 0,707, 0]. Ou seja, normalização é a redução de um vetor para um comprimento de 1 (comprimento unitário) sem alterar sua direção. Observe que os vetores [0,707, 0,707, 0] e [1, 1, 0] apontam na mesma direção, ou seja, o personagem se moverá estritamente para a direita nos dois casos, mas o vetor [0,707, 0,707, 0] é normalizado e a velocidade do caractere Agora será igual a 1, o que elimina o erro com o movimento diagonal acelerado. É sempre recomendável normalizar o vetor antes de qualquer cálculo para evitar vários tipos de erros. Vamos ver como normalizar um vetor. É necessário dividir cada um de seus componentes (X, Y, Z) pelo seu comprimento. A função de encontrar o comprimento já está lá, metade do trabalho está feito,agora escrevemos a função de normalização do vetor (dentro da classe Vector):normalize() {
const length = this.getLength();
this.x /= length;
this.y /= length;
this.z /= length;
return this;
}
O método normalize normaliza o vetor e o retorna (this), isso é necessário para que, no futuro, seja possível usar normalize nas expressões.Agora que sabemos o que é a normalização de um vetor e sabemos que é melhor executá-lo antes de usar o vetor, surge a questão. Se a normalização de um vetor é uma redução no comprimento de uma unidade, ou seja, a velocidade de movimento de um objeto (caractere) será igual a 1, como acelerar o caractere? Por exemplo, ao mover um personagem na diagonal para cima / direita a uma velocidade de 1, seu vetor será [0,707, 0,707, 0], e qual será o vetor se quisermos mover o personagem 6 vezes mais rápido? Para fazer isso, há uma operação chamada "multiplicar um vetor por um escalar". O escalar é o número usual pelo qual o vetor é multiplicado. Se o escalar for igual a 6, o vetor se tornará 6 vezes mais longo e nosso personagem será 6 vezes mais rápido, respectivamente. Como fazer multiplicação escalar? Para isso, é necessário multiplicar cada componente do vetor por um escalar. Por exemplo, resolvemos o problema acima,quando um caractere que se move para um vetor [0,707, 0,707, 0] (velocidade 1) precisa ser acelerado 6 vezes, ou seja, multiplique o vetor pelo escalar 6. A fórmula para multiplicar o vetor "V" pelo escalar "s" é a seguinte:
No nosso caso, será:- um novo vetor de deslocamento cujo comprimento é 6.É importante saber que um escalar positivo escala um vetor sem alterar sua direção; se um escalar é negativo, ele também escala um vetor (aumenta seu comprimento), mas também altera a direção do vetor para o oposto.Vamos implementar a função de multiplyByScalarmultiplicar um vetor por um escalar em nossa classe Vector:multiplyByScalar(s) {
this.x *= s;
this.y *= s;
this.z *= s;
return this;
}
O Matrix
Descobrimos um pouco com vetores e algumas operações neles que serão necessários neste artigo. Em seguida, você precisa lidar com matrizes.Podemos dizer que uma matriz é a matriz bidimensional mais comum. É apenas que na programação eles usam o termo “matriz bidimensional” e, em matemática, eles usam a “matriz”. Por que as matrizes são necessárias na programação 3D? Analisaremos isso assim que aprendermos a trabalhar um pouco com eles. Usaremos apenas matrizes numéricas (uma matriz de números). Cada matriz tem seu próprio tamanho (como qualquer matriz bidimensional). Aqui estão alguns exemplos de matrizes:De todas as operações em matrizes, agora consideramos apenas a multiplicação (o restante posteriormente). Acontece que a multiplicação de matrizes não é a operação mais fácil, ela pode ser facilmente confundida se você não seguir cuidadosamente a ordem de multiplicação. Mas não se preocupe, você terá sucesso, porque aqui apenas multiplicaremos e resumiremos. Para começar, precisamos lembrar alguns recursos de multiplicação que precisamos:- Se tentarmos multiplicar o número A pelo número B, então é o mesmo que B * A. Se reorganizarmos os operandos e o resultado não mudar sob nenhuma ação, eles dizem que a operação é comutativa. Exemplo: a + b = b + a operação é comutativa, a - b ≠ b - a operação não é comutativa, a * b = b * a operação de números multiplicadores é comutativa. Portanto, a operação de multiplicação de matrizes é não comutativa, em contraste com a multiplicação de números. Ou seja, multiplicar a matriz M pela matriz N não será igual à multiplicação da matriz N por M.
- A multiplicação da matriz é possível se o número de colunas da primeira matriz (à esquerda) for igual ao número de linhas na segunda matriz (à direita).
Agora, examinaremos o segundo recurso da multiplicação de matrizes (quando a multiplicação é possível). Aqui estão alguns exemplos que demonstram quando a multiplicação é possível e quando não:Acho que esses exemplos esclareceram um pouco a imagem quando a multiplicação é possível. O resultado da multiplicação de matrizes sempre será uma matriz, cujo número de linhas será igual ao número de linhas da 1ª matriz e o número de colunas é igual ao número de colunas da 2ª. Por exemplo, se multiplicarmos a matriz 2 por 6 e 6 por 8, obteremos uma matriz de tamanho 2 por 8. Agora vamos diretamente para a multiplicação em si.Para multiplicação, é importante lembrar que as colunas e linhas na matriz são numeradas a partir de 1 e na matriz de 0. O primeiro índice no elemento da matriz indica o número da linha e o segundo o número da coluna. Ou seja, se o elemento da matriz (elemento da matriz) for escrito como: m28, isso significa que passamos para a segunda linha e a oitava coluna. Mas, como trabalharemos com matrizes no código, toda a indexação de linhas e colunas começará em 0.Vamos tentar multiplicar 2 matrizes A e B com tamanhos e elementos específicos:
Pode-se observar que a matriz A possui tamanho de 3 por 2 e a matriz B possui tamanho de 2 por 2, e é possível multiplicar:
Como você pode ver, temos uma matriz 3 por 2, a multiplicação é inicialmente confusa, mas se houver um objetivo de aprender a multiplicar “sem estresse”, vários exemplos precisam ser resolvidos. Aqui está outro exemplo de multiplicação das matrizes A e B:
Se a multiplicação não estiver completamente clara, tudo bem, porque não precisamos multiplicar por folha. Escreveremos uma vez a função de multiplicação da matriz e a usaremos. Em geral, todas essas funções já estão escritas, mas fazemos tudo por conta própria.Agora, mais alguns termos que serão usados no futuro:- Uma matriz quadrada é uma matriz na qual o número de linhas é igual ao número de colunas, aqui está um exemplo de matrizes quadradas:
- A diagonal principal de uma matriz quadrada é chamada de todos os elementos da matriz cujo número de linha é igual ao número da coluna. Exemplos de diagonais (neste exemplo, a diagonal principal é preenchida com nove):
- Uma matriz unitária é uma matriz quadrada na qual todos os elementos da diagonal principal são 1 e todos os outros são 0. Exemplos de matrizes unitárias:
Também é importante lembrar dessa propriedade que, se multiplicarmos qualquer matriz M por uma matriz unitária de tamanho adequado, por exemplo, chamá-la I, obteremos a matriz original M, por exemplo: M * I = M ou I * M = M. Ou seja, multiplicar a matriz pela matriz de identidade não afeta o resultado. Voltaremos à matriz de identidade mais tarde. Na programação 3D, geralmente usamos uma matriz quadrada de 4 por 4.Agora, vejamos por que precisaremos de matrizes e por que multiplicá-las? Na programação 3D, existem muitas matrizes 4 por 4 diferentes que, se multiplicadas por um vetor ou ponto, executam as ações que precisamos. Por exemplo, precisamos girar o caractere no espaço tridimensional ao redor do eixo X, como fazer isso? Multiplique o vetor por uma matriz especial, responsável pela rotação em torno do eixo X. Se você precisar mover e girar um ponto em torno da origem, será necessário multiplicar esse ponto por uma matriz especial. As matrizes têm uma excelente propriedade - combinando transformações (consideraremos neste artigo). Suponha que precisamos de um caractere composto de 100 pontos (vértices, mas também será um pouco menor) na aplicação, aumente 5 vezes, gire 90 graus X e mova-o 30 unidades.Como já mencionado, para diferentes ações já existem matrizes especiais que consideraremos. Para concluir a tarefa acima, por exemplo, percorremos todos os 100 pontos e cada um multiplicamos pela primeira matriz para aumentar o caractere, depois multiplicamos pela segunda matriz para girar 90 graus em X, depois multiplicamos por 3 th para mover 30 unidades para cima. No total, para cada ponto, temos 3 multiplicações de matriz e 100 pontos, o que significa que haverá 300 multiplicações, mas se pegarmos e multiplicarmos as matrizes para aumentar 5 vezes, gire 90 graus ao longo de X e mova 30 unidades. , obtemos uma matriz que contém todas essas ações. Multiplicando um ponto por essa matriz, o ponto estará onde é necessário. Agora vamos calcular quantas ações são realizadas: 2 multiplicações para 3 matrizes e 100 multiplicações para 100 pontos,um total de 102 multiplicações é definitivamente melhor do que 300 multiplicações antes disso. O momento em que multiplicamos 3 matrizes para combinar ações diferentes em uma matriz - é chamado de combinação de transformações e certamente o faremos com um exemplo.Como multiplicar a matriz pela matriz, examinamos, mas o parágrafo lido acima fala da multiplicação da matriz por um ponto ou vetor. Para multiplicar um ponto ou vetor, basta representá-los como uma matriz.Por exemplo, temos um vetor [10, 2, 5] e há uma matriz:
Pode-se observar que o vetor pode ser representado por uma matriz de 1 por 3 ou por uma matriz de 3 por 1. Portanto, podemos multiplicar o vetor por uma matriz de 2 maneiras:Como você pode ver, podemos representar o vetor como um vetor de linha e multiplicá-lo por uma matriz ou representar o vetor como um vetor de coluna e multiplicar a matriz por ele. Vamos verificar se o resultado da multiplicação será o mesmo nos dois casos:Multiplique o vetor de linha pela matriz:
Agora, multiplique a matriz pelo vetor da coluna:
Vemos que, multiplicando o vetor de linha pela matriz e a matriz pelo vetor de coluna, obtivemos resultados completamente diferentes (lembramos a comutatividade). Portanto, na programação 3D, existem matrizes projetadas para serem multiplicadas apenas por um vetor de linha ou apenas por um vetor de coluna. Se multiplicarmos a matriz destinada ao vetor de linha pelo vetor de coluna, obteremos um resultado que não nos fornecerá nada. Use a representação vetorial / ponto conveniente para você (linha ou coluna); somente no futuro, use as matrizes apropriadas para sua representação vetorial / ponto. O Direct3D, por exemplo, usa uma representação de seqüência de vetores, e todas as matrizes no Direct3D são projetadas para multiplicar um vetor de linha por uma matriz. O OpenGL usa uma representação de um vetor (ou ponto) como uma coluna,e todas as matrizes são projetadas para multiplicar a matriz por um vetor de coluna. Nos artigos, usaremos o vetor da coluna e multiplicaremos a matriz pelo vetor da coluna.Para resumir o que lemos sobre a matriz.- Para executar uma ação em um vetor (ou ponto), existem matrizes especiais, algumas das quais veremos neste artigo.
- Para combinar a transformação (deslocamento, rotação etc.), podemos multiplicar as matrizes de cada transformação e obter uma matriz que contenha todas as transformações juntas.
- Na programação 3D, usaremos constantemente matrizes de 4 por 4 quadrados.
- Podemos multiplicar a matriz por um vetor (ou ponto), representando-a como uma coluna ou linha. Mas para o vetor de coluna e vetor de linha, você precisa usar matrizes diferentes.
Após uma pequena análise das matrizes, vamos adicionar uma classe de matriz 4 por 4 e implementar métodos para multiplicar a matriz pela matriz e o vetor pela matriz. Usaremos o tamanho da matriz 4 por 4, porque todas as matrizes padrão usadas para várias ações (movimento, rotação, escala, ...) são desse tamanho, não precisamos de matrizes de tamanho diferente. Vamos adicionar a classe Matrix ao projeto. Às vezes, ainda assim, a classe para trabalhar com matrizes 4 por 4 é chamada Matrix4, e esses 4 no título nos dizem sobre o tamanho da matriz (eles também dizem a matriz de 4ª ordem). Todos os dados da matriz serão armazenados em uma matriz bidimensional 4 por 4.Nos voltamos para a implementação de operações de multiplicação. Eu não recomendo usar loops para isso. Para melhorar o desempenho, todos temos que multiplicar linha por linha - isso acontecerá devido ao fato de que todas as multiplicações ocorrerão com matrizes de tamanho fixo. Usarei ciclos para a operação de multiplicação, apenas para economizar a quantidade de código, você pode escrever toda a multiplicação sem ciclos. Meu código de multiplicação fica assim:class Matrix {
static multiply(a, b) {
const m = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
];
for (let i = 0; i < 4; i++) {
for (let j = 0; j < 4; j++) {
m[i][j] = a[i][0] * b[0][j] +
a[i][1] * b[1][j] +
a[i][2] * b[2][j] +
a[i][3] * b[3][j];
}
}
return m;
}
}
Como você pode ver, o método pega as matrizes aeb, multiplica-as e retorna o resultado na mesma matriz 4 por 4. No início do método, criei uma matriz m preenchida com zeros, mas isso não é necessário, então eu queria mostrar qual dimensão o resultado será, você Você pode criar uma matriz 4 por 4 sem nenhum dado.Agora você precisa implementar a multiplicação da matriz pelo vetor da coluna, conforme discutido acima. Mas se você representa o vetor como uma coluna, obtém uma matriz do formulário:pelo qual precisaremos multiplicar por 4 por 4 matrizes para executar várias ações. Mas neste exemplo, é visto claramente que essa multiplicação não pode ser realizada, porque o vetor da coluna possui 3 linhas e a matriz possui 4 colunas. O que fazer então? Algum quarto elemento é necessário, então o vetor terá 4 linhas, que serão iguais ao número de colunas na matriz. Vamos adicionar esse quarto parâmetro ao vetor e chamá-lo de W, agora temos todos os vetores 3D da forma [X, Y, Z, W] e esses vetores já podem ser multiplicados pela matriz 4 por 4. Na verdade, o componente W um propósito mais profundo, mas o conheceremos na próxima parte (não é à toa que temos uma matriz 4 por 4, não matriz 3 por 3). Adicione à classe Vector, que criamos acima do componente w. Agora, o início da classe Vector fica assim:class Vector {
x = 0;
y = 0;
z = 0;
w = 1;
constructor(x, y, z, w = 1) {
this.x = x;
this.y = y;
this.z = z;
this.w = w;
}
Inicializei W em um, mas por que 1? Se observarmos como os componentes da matriz e do vetor são multiplicados (o exemplo de código abaixo), você poderá ver que, se definir W como 0 ou qualquer outro valor que não seja 1, ao multiplicar esse W afetará o resultado, mas não o fazemos. sabemos como usá-lo e, se o fizermos 1, ele estará no vetor, mas o resultado não será alterado de forma alguma. Agora, de volta à matriz e implemente na classe Matrix (você também pode na classe Vector, não há diferença) a matriz é multiplicada por um vetor, o que já é possível, graças a W:static multiplyVector(m, v) {
return new Vector(
m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
)
}
Observe que apresentamos a matriz como uma matriz de 4 por 4 e o vetor como um objeto com as propriedades x, y, z, w. No futuro, alteraremos o vetor e ele também será representado por uma matriz de 1 por 4, porque isso acelerará a multiplicação. Mas agora, para ver melhor como ocorre a multiplicação e melhorar a compreensão do código, não mudaremos o vetor.Escrevemos o código para multiplicação de matrizes entre nós e multiplicação de vetores de matrizes, mas ainda não está claro como isso nos ajudará nos gráficos tridimensionais.Também quero lembrá-lo de que chamo um vetor de ponto (posição no espaço) e de direção, porque ambos os objetos contêm a mesma estrutura de dados x, y, z e o recém-introduzido w. Vejamos algumas das matrizes que executam operações básicas em vetores. A primeira dessas matrizes será a matriz de tradução. Multiplicando a matriz de deslocamento por um vetor (localização), ela mudará de acordo com o número especificado de unidades no espaço. E aqui está a matriz de deslocamento:
Onde dx, dy, dz significam deslocamentos ao longo dos eixos x, y, z, respectivamente, essa matriz é projetada para ser multiplicada por um vetor de coluna. Essas matrizes podem ser encontradas na Internet ou em qualquer literatura sobre programação em 3D, não precisamos criá-las, tomá-las agora, como as fórmulas que você usa da escola que você só precisa saber ou entender por que usá-las. Vamos verificar se, de fato, multiplicando essa matriz por um vetor, ocorrerá um deslocamento. Tome como vetor que vamos mover o vetor [10, 10, 10, 1] (sempre deixamos o 4º parâmetro W sempre 1), suponha que esta seja a posição do nosso personagem no jogo e queremos alterá-lo 10 unidades para cima, 5 unidades à direita e a 1 unidade de distância da tela. Então o vetor de deslocamento será assim [10, 5, -1] (-1 porque temos um sistema de coordenadas para a direita e o Z adicional,quanto menor for). Se calcularmos o resultado sem matrizes, pela soma usual de vetores. Isso resultará no seguinte resultado: [10 + 10, 10 + 5, 10 + -1, 1] = [20, 15, 9, 1] - essas são as novas coordenadas do nosso personagem. Multiplicando a matriz acima pelas coordenadas iniciais [10, 10, 10, 1], devemos obter o mesmo resultado, vamos verificar isso no código, escrever a multiplicação após as classes Drawer, Vector e Matrix:const translationMatrix = [
[1, 0, 0, 10],
[0, 1, 0, 5],
[0, 0, 1, -1],
[0, 0, 0, 1],
]
const characterPosition = new Vector(10, 10, 10)
const newCharacterPosition = Matrix.multiplyVector(
translationMatrix, characterPosition
)
console.log(newCharacterPosition)
Neste exemplo, substituímos o deslocamento de caractere desejado (translationMatrix) na matriz de deslocamento, inicializamos sua posição inicial (characterPosition) e o multiplicamos pela matriz, e o resultado foi gerado pelo console.log (este é o resultado da depuração em JS). Se você usa não-JS, produza X, Y, Z você mesmo usando as ferramentas do seu idioma. O resultado que obtivemos no console: [20, 15, 9, 1], tudo concorda com o resultado que calculamos acima. Você pode ter uma pergunta: por que obter o mesmo resultado multiplicando o vetor por uma matriz especial? Se obtivemos isso muito mais facilmente, somando o vetor com um componente de deslocamento. A resposta não é a mais simples e discutiremos mais detalhadamente, mas agora pode-se notar que, como discutido anteriormente, podemos combinar matrizes com diferentes transformações entre si,reduzindo assim muitos cálculos. No exemplo acima, criamos a matriz translationMatrix como uma matriz manualmente e substituímos o deslocamento necessário lá, mas como frequentemente usamos essa e outras matrizes, vamos colocá-la em um método na classe Matrix e passar o deslocamento para ela com argumentos:static getTranslation(dx, dy, dz) {
return [
[1, 0, 0, dx],
[0, 1, 0, dy],
[0, 0, 1, dz],
[0, 0, 0, 1],
]
}
Dê uma olhada na matriz de deslocamento, você verá que dx, dy, dz estão na última coluna e se observarmos o código para multiplicar a matriz por um vetor, perceberemos que essa coluna é multiplicada pelo componente W do vetor. E se fosse, por exemplo, 0, então dx, dy, dz, multiplicaríamos por 0 e a mudança não funcionaria. Mas podemos fazer W igual a 0 se queremos armazenar a direção na classe Vector, porque é impossível mover a direção, para nos protegermos, e mesmo se multiplicarmos essa direção pela matriz de deslocamento, isso não quebrará o vetor de direção, porque todo o movimento será multiplicado por 0. Nototal, podemos aplicar essa regra, criamos um local como este:new Vector(x, y, z, 1)
E criaremos a direção assim:new Vector(x, y, z, 0)
Assim, podemos distinguir entre localização e direção e, quando multiplicamos a direção pela matriz de deslocamento, não quebramos acidentalmente o vetor de direção.Vértices e índices
Antes de vermos o que são outras matrizes, veremos um pouco como aplicar nosso conhecimento existente para exibir algo tridimensional na tela. Tudo o que deduzimos antes disso são linhas e pixels. Mas agora vamos usar essas ferramentas para derivar, por exemplo, um cubo. Para fazer isso, precisamos descobrir em que consiste um modelo tridimensional. O componente mais básico de qualquer modelo 3D são os pontos (chamaremos os vértices abaixo) ao longo dos quais podemos desenhá-lo; esses são, de fato, muitos vetores de localização, que, se os conectamos corretamente às linhas, obtemos um modelo 3D (grade do modelo ) na tela, ela ficará sem textura e sem muitas outras propriedades, mas tudo terá seu tempo. Dê uma olhada no cubo que queremos gerar e tente entender quantos vértices ele possui: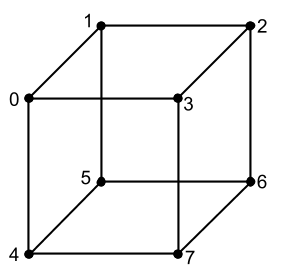
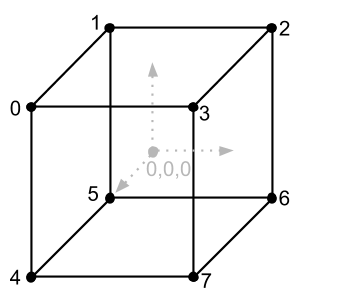
const vertices = [
new Vector(-1, 1, 1),
new Vector(-1, 1, -1),
new Vector(1, 1, -1),
new Vector(1, 1, 1),
new Vector(-1, -1, 1),
new Vector(-1, -1, -1),
new Vector(1, -1, -1),
new Vector(1, -1, 1),
];
Coloquei cada vértice em uma instância da classe Vector, essa não é a melhor opção para desempenho (melhor em uma matriz), mas agora nosso objetivo é descobrir como tudo funciona.Vamos agora pegar as coordenadas dos vértices do cubo como pixels que desenharemos na tela. Nesse caso, vemos que o tamanho do cubo é de 2 por 2 por 2 pixels. Criamos um cubo tão pequeno para que veja o trabalho da matriz de escala, com a qual iremos aumentá-la. No futuro, é uma prática muito boa fazer modelos pequenos, ainda menores que os nossos, para aumentá-los para o tamanho desejado com escalares não muito diferentes.Só que desenhar os pontos do cubo com pixels não é muito claro, porque tudo o que veremos são 8 pixels, um para cada vértice, é muito melhor desenhar um cubo com linhas usando a função drawLine do artigo anterior. Mas, para isso, precisamos entender de quais vértices para quais linhas passamos. Dê uma olhada na imagem do cubo com os índices novamente e veremos que ele consiste em 12 linhas (ou arestas). Também é muito fácil ver que conhecemos as coordenadas do início e do fim de cada linha. Por exemplo, uma das linhas (superior próxima) deve ser desenhada do vértice 0 ao vértice 3 ou das coordenadas [-1, 1, 1] às coordenadas [1, 1, 1]. Teremos que escrever informações sobre cada linha no código, visualizando manualmente a imagem do cubo, mas como fazer isso certo? Se tivermos 12 linhas e cada linha tiver um começo e um fim, ou seja, 2 pontos, então,desenhar um cubo precisamos de 24 pontos? Esta é a resposta correta, mas vamos dar uma olhada na imagem do cubo novamente e prestar atenção ao fato de que cada linha do cubo possui vértices comuns, por exemplo, no vértice 0 3 linhas estão conectadas, e assim por cada vértice. Podemos economizar memória e não anotar as coordenadas do início e do fim de cada linha, basta criar uma matriz e especificar os índices de vértices da matriz de vértices na qual essas linhas começam e terminam. Vamos criar uma matriz desse tipo e descrevê-la apenas com índices de vértices, 2 índices por linha (o início da linha e o final). E um pouco mais adiante, quando desenhamos essas linhas, podemos obter facilmente suas coordenadas a partir da matriz de vértices. Minha matriz de linhas (eu a chamei de bordas, porque essas são as bordas do cubo) Criei uma matriz de vértices abaixo e fica assim:mas vamos dar uma olhada na imagem do cubo novamente e prestar atenção ao fato de que cada linha do cubo possui vértices comuns, por exemplo, no vértice 0 3 linhas estão conectadas, e assim por cada vértice. Podemos economizar memória e não anotar as coordenadas do início e do fim de cada linha, basta criar uma matriz e especificar os índices de vértices da matriz de vértices na qual essas linhas começam e terminam. Vamos criar uma matriz desse tipo e descrevê-la apenas com índices de vértices, 2 índices por linha (o início da linha e o final). E um pouco mais adiante, quando desenhamos essas linhas, podemos obter facilmente suas coordenadas a partir da matriz de vértices. Minha matriz de linhas (eu a chamei de bordas, porque essas são as bordas do cubo) Criei uma matriz de vértices abaixo e fica assim:mas vamos dar uma olhada na imagem do cubo novamente e prestar atenção ao fato de que cada linha do cubo possui vértices comuns, por exemplo, no vértice 0 3 linhas estão conectadas, e assim por cada vértice. Podemos economizar memória e não anotar as coordenadas do início e do fim de cada linha, basta criar uma matriz e especificar os índices de vértices da matriz de vértices na qual essas linhas começam e terminam. Vamos criar uma matriz desse tipo e descrevê-la apenas com índices de vértices, 2 índices por linha (o início da linha e o final). E um pouco mais adiante, quando desenhamos essas linhas, podemos obter facilmente suas coordenadas a partir da matriz de vértices. Minha matriz de linhas (eu a chamei de bordas, porque essas são as bordas do cubo) Criei uma matriz de vértices abaixo e fica assim:e assim com cada vértice. Podemos economizar memória e não anotar as coordenadas do início e do fim de cada linha, basta criar uma matriz e especificar os índices de vértices da matriz de vértices na qual essas linhas começam e terminam. Vamos criar uma matriz desse tipo e descrevê-la apenas com índices de vértices, 2 índices por linha (o início da linha e o final). E um pouco mais adiante, quando desenhamos essas linhas, podemos obter facilmente suas coordenadas a partir da matriz de vértices. Minha matriz de linhas (eu a chamei de bordas, porque essas são as bordas do cubo) Criei uma matriz de vértices abaixo e fica assim:e assim com cada vértice. Podemos economizar memória e não anotar as coordenadas do início e do fim de cada linha, basta criar uma matriz e especificar os índices de vértices da matriz de vértices na qual essas linhas começam e terminam. Vamos criar uma matriz desse tipo e descrevê-la apenas com índices de vértices, 2 índices por linha (o início da linha e o final). E um pouco mais adiante, quando desenhamos essas linhas, podemos obter facilmente suas coordenadas a partir da matriz de vértices. Minha matriz de linhas (eu a chamei de bordas, porque essas são as bordas do cubo) Criei uma matriz de vértices abaixo e fica assim:2 índices em cada linha (o início da linha e o final). E um pouco mais adiante, quando desenhamos essas linhas, podemos obter facilmente suas coordenadas a partir da matriz de vértices. Minha matriz de linhas (eu a chamei de bordas, porque essas são as bordas do cubo) Eu criei uma matriz de vértices abaixo e fica assim:2 índices em cada linha (o início da linha e o final). E um pouco mais adiante, quando desenhamos essas linhas, podemos obter facilmente suas coordenadas a partir da matriz de vértices. Minha matriz de linhas (eu a chamei de bordas, porque essas são as bordas do cubo) Criei uma matriz de vértices abaixo e fica assim:
const edges = [
[0, 1],
[1, 2],
[2, 3],
[3, 0],
[0, 4],
[1, 5],
[2, 6],
[3, 7],
[4, 5],
[5, 6],
[6, 7],
[7, 4],
];
Existem 12 pares de índices nessa matriz, 2 índices de vértice por linha.Vamos nos familiarizar com outra matriz que aumentará nosso cubo e, finalmente, tentar desenhá-lo na tela. A Matriz de Escala fica assim:
Os parâmetros sx, sy, sz na diagonal principal significam quantas vezes queremos aumentar o objeto. Se substituirmos 10, 10, 10 na matriz em vez de sx, sy, sz e multiplicar essa matriz pelos vértices do cubo, isso tornará nosso cubo dez vezes maior e não será mais 2 por 2 por 2, mas 20 por 20 por 20.Para a matriz de escala, bem como para a matriz de deslocamento, implementamos o método na classe Matrix, que retornará a matriz com os argumentos já substituídos:static getScale(sx, sy, sz) {
return [
[sx, 0, 0, 0],
[0, sy, 0, 0],
[0, 0, sz, 0],
[0, 0, 0, 1],
]
}
Transportador de visualização
Se agora tentarmos desenhar um cubo com linhas usando as coordenadas atuais dos vértices, obteremos um cubo muito pequeno de dois pixels no canto superior esquerdo da tela, porque a origem da tela está lá. Vamos percorrer todos os vértices do cubo e multiplicá-los pela matriz de escala para aumentar o cubo e depois pela matriz de deslocamento para ver o cubo não no canto superior esquerdo, mas no meio da tela, tenho o código para enumerar vértices com multiplicação de matrizes abaixo matriz de arestas e fica assim:const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
Matrix.getScale(100, 100, 100),
vertices[i]
);
vertex = Matrix.multiplyVector(
Matrix.getTranslation(400, -300, 0),
vertex
);
sceneVertices.push(vertex);
}
Observe que não alteramos os vértices originais do cubo, mas salvamos o resultado da multiplicação na matriz sceneVertices, porque podemos desenhar vários cubos de tamanhos diferentes em coordenadas diferentes e, se alterarmos as coordenadas originais, não poderemos desenhar o próximo cubo, t .para. não há nada para começar, as coordenadas iniciais serão corrompidas pelo primeiro cubo. No código acima, aumentei o cubo original em 100 vezes em todas as direções, multiplicando todos os vértices pela matriz de escala com argumentos 100, 100, 100 e também movi todos os vértices do cubo para a direita e abaixei em 400 e -300 pixels, respectivamente, pois temos os tamanhos de tela do artigo anterior são de 800 por 600, serão apenas metade da largura e altura da área de desenho, ou seja, o centro.Nós terminamos os vértices até agora, mas ainda precisamos desenhar tudo isso usando drawLine e a matriz de bordas, vamos escrever outro loop abaixo do loop de vértices para iterar sobre as arestas e desenhar todas as linhas:drawer.clearSurface()
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i]
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
)
}
ctx.putImageData(imageData, 0, 0)
Lembre-se de que, no último artigo, começamos todo o desenho limpando a tela do estado anterior, chamando o método clearSurface, iteramos em todas as faces do cubo e desenhei o cubo com linhas azuis (0, 0, 255) e tomo as coordenadas das linhas da matriz sceneVertices, t .para. já existem vértices escalados e movidos no ciclo anterior, mas os índices desses vértices coincidem com os índices dos vértices originais da matriz de vértices, porque Eu os processei e os coloquei na matriz sceneVertices sem alterar a ordem. Se rodarmos o código agora, não veremos nada na tela. Isso ocorre porque, em nosso sistema de coordenadas, Y olha para cima e, no sistema de coordenadas, a tela olha para baixo. Acontece que existe o nosso cubo, mas está fora da tela e, para corrigir isso, precisamos inverter a imagem em Y (espelho) antes de desenhar um pixel na classe Drawer. Até agora, essa opção será suficiente para nós, como resultado, o código para desenhar um pixel para mim é assim:drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
Pode-se ver que na fórmula para obter o deslocamento, Y está agora com um sinal de menos e o eixo agora está na direção que precisamos, também neste método, adicionei uma verificação para ir além dos limites da matriz de pixels. Algumas outras otimizações apareceram na classe Drawer devido aos comentários do artigo anterior, então eu posto a classe Drawer inteira com algumas otimizações e você pode substituir a antiga Drawer por esta:Código de classe de gaveta aprimoradoclass Drawer {
surface = null;
width = 0;
height = 0;
constructor(surface, width, height) {
this.surface = surface;
this.width = width;
this.height = height;
}
drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
const round = Math.trunc;
x1 = round(x1);
y1 = round(y1);
x2 = round(x2);
y2 = round(y2);
const c1 = y2 - y1;
const c2 = x2 - x1;
const length = Math.max(
Math.abs(c1),
Math.abs(c2)
);
const xStep = c2 / length;
const yStep = c1 / length;
for (let i = 0 ; i <= length ; i++) {
this.drawPixel(
Math.trunc(x1 + xStep * i),
Math.trunc(y1 + yStep * i),
r, g, b,
);
}
}
clearSurface() {
const surfaceSize = this.width * this.height * 4;
for (let i = 0; i < surfaceSize; i++) {
this.surface[i] = 0;
}
}
}
const drawer = new Drawer(
imageData.data,
imageData.width,
imageData.height
);
Se você executar o código agora, a seguinte imagem aparecerá na tela:Aqui você pode ver que há um quadrado no centro, embora esperássemos obter um cubo, qual é o problema? De fato - este é o cubo, ele fica perfeitamente perfeitamente alinhado com uma das faces (laterais) em nossa direção, para que não vejamos o resto. Além disso, ainda não nos familiarizamos com as projeções e, portanto, a face traseira do cubo não se torna menor com a distância, como na vida real. Para garantir que este seja realmente um cubo, vamos rotacioná-lo um pouco para que pareça com a imagem que vimos anteriormente quando criamos a matriz de vértices. Para girar a imagem 3D, você pode usar 3 matrizes especiais, porque podemos girar em torno de um dos eixos X, Y ou Z, o que significa que para cada eixo haverá sua própria matriz de rotação (existem outras formas de rotação, mas este é o tópico dos próximos artigos). Aqui está a aparência dessas matrizes:Se multiplicarmos os vértices do cubo por uma dessas matrizes, o cubo girará pelo ângulo especificado (a) ao redor do eixo, a matriz de rotação em torno da qual escolheremos. Existem alguns recursos ao girar vários eixos ao mesmo tempo, e nós os examinaremos abaixo. Como você pode ver no exemplo da matriz, eles usam 2 funções sin e cos, e o JavaScript já possui uma funcionalidade para calcular Math.sin (a) e Math.cos (a), mas eles funcionam com medidas radiais de ângulos, o que pode não parecer o mais conveniente se quisermos girar o modelo. Por exemplo, é muito mais conveniente girar algo em 90 graus (medida em graus), o que em uma medida em radiano significaPi / 2(Também existe um valor Pi aproximado em JS, esta é a constante Math.PI). Vamos adicionar 3 métodos à classe Matrix para obter matrizes de rotação, com um ângulo de rotação aceito em graus, que converteremos em radianos, porque eles são necessários para que as funções sin / cos funcionem:static getRotationX(angle) {
const rad = Math.PI / 180 * angle;
return [
[1, 0, 0, 0],
[0, Math.cos(rad), -Math.sin(rad), 0],
[0, Math.sin(rad), Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationY(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), 0, Math.sin(rad), 0],
[0, 1, 0, 0],
[-Math.sin(rad), 0, Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationZ(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), -Math.sin(rad), 0, 0],
[Math.sin(rad), Math.cos(rad), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
];
}
Todos os três métodos começam com a conversão de graus em radianos, após o que substituímos o ângulo de rotação em radianos na matriz de rotação, passando os ângulos para as funções sin e cos. Por que a matriz é exatamente essa, você pode ler mais no hub nos artigos temáticos, com uma explicação muito detalhada, caso contrário, você pode perceber essas matrizes como fórmulas que foram calculadas para nós e podemos ter certeza de que estão funcionando.Acima no código, implementamos 2 ciclos, o primeiro converte vértices, o segundo desenha linhas por índices de vértices; como resultado, obtemos uma imagem dos vértices na tela e vamos chamar esta seção do código de pipeline de visualização. O transportador porque pegamos o pico e, por sua vez, fazemos operações diferentes com ele, escala, deslocamento, rotação, renderização, como em um transportador industrial normal. Agora, vamos adicionar ao primeiro ciclo no pipeline de visualização, além de escalar, girar em torno dos eixos. Primeiro, vou girar em torno de X, depois em torno de Y, depois aumentar o modelo e movê-lo (as duas últimas ações já estão lá), para que todo o código do loop fique assim:for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
Matrix.getRotationX(20),
vertices[i]
);
vertex = Matrix.multiplyVector(
Matrix.getRotationY(20),
vertex
);
vertex = Matrix.multiplyVector(
Matrix.getScale(100, 100, 100),
vertex
);
vertex = Matrix.multiplyVector(
Matrix.getTranslation(400, -300, 0),
vertex
);
sceneVertices.push(vertex);
}
Neste exemplo, girei todos os vértices ao redor do eixo X em 20 graus, depois em torno de Y em 20 graus e eu já tinha duas transformações restantes. Se você fez tudo corretamente, seu cubo deve agora parecer tridimensional:Girar os eixos tem um recurso, por exemplo, se você girar o cubo primeiro ao redor do eixo Y e depois ao redor do eixo X, os resultados serão diferentes:Existem outros recursos, por exemplo, se você girar o cubo 90 graus no eixo X, depois 90 graus no eixo Y e, finalmente, 90 graus ao redor do eixo Z, a última rotação em torno de Z cancelará a rotação em torno de X e você obterá o mesmo o resultado é como se você tivesse girado a figura 90 graus em torno do eixo Y. Para ver por que isso acontece, pegue qualquer objeto retangular (ou cúbico) em suas mãos (por exemplo, o cubo de Rubik montado), lembre-se da posição inicial do objeto e gire-o 90 graus primeiro em torno do X imaginário e, em seguida, 90 graus em torno de Y e 90 graus em torno de Z e lembre-se de que lado ele se tornou para você, comece da posição inicial que você lembrou anteriormente e faça o mesmo, removendo as curvas de X e Z, gire apenas em torno de Y - você verá que o resultado é o mesmo.Agora, não resolveremos esse problema e entraremos em detalhes, atualmente essa rotação é completamente satisfatória para nós, mas mencionaremos esse problema na terceira parte (se você quiser entender mais agora, tente procurar artigos no hub com a consulta "trava articulada") .Agora vamos otimizar um pouco o nosso código, foi mencionado acima que as transformações de matriz podem ser combinadas entre si multiplicando matrizes de transformação. Vamos tentar não multiplicar cada vetor primeiro pela matriz de rotação em torno de X, depois em torno de Y, depois escalando e no final do movimento, e primeiro, antes do loop, multiplicamos todas as matrizes e, no loop, multiplicaremos cada vértice por apenas uma matriz resultante, tenho o código saiu assim:let matrix = Matrix.getRotationX(20);
matrix = Matrix.multiply(
Matrix.getRotationY(20),
matrix
);
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
);
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
);
const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
);
sceneVertices.push(vertex);
}
Neste exemplo, a combinação de transformações é realizada 1 vez antes do ciclo e, portanto, temos apenas 1 multiplicação de matriz com cada vértice. Se você executar esse código, o padrão do cubo deve permanecer o mesmo.Vamos adicionar a animação mais simples, a saber, alteraremos o ângulo de rotação em torno do eixo Y no intervalo, por exemplo, alteraremos o ângulo de rotação em torno do eixo Y em 1 grau, a cada 100 milissegundos. Para fazer isso, coloque o código do pipeline de visualização na função setInterval, que usamos no primeiro artigo. O código do pipeline de animação fica assim:let angle = 0
setInterval(() => {
let matrix = Matrix.getRotationX(20)
matrix = Matrix.multiply(
Matrix.getRotationY(angle += 1),
matrix
)
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
)
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
)
const sceneVertices = []
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
)
sceneVertices.push(vertex)
}
drawer.clearSurface()
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i]
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
)
}
ctx.putImageData(imageData, 0, 0)
}, 100)
O resultado deve ser assim:A última coisa que faremos nesta parte é exibir os eixos do sistema de coordenadas na tela para que fique visível em torno do qual nosso cubo gira. Desenhamos o eixo Y do centro para cima, 200 pixels de comprimento, o eixo X, para a direita, também 200 pixels de comprimento, e o eixo Z, desenha 150 pixels para baixo e para a esquerda (na diagonal), conforme mostrado no início do artigo na figura do sistema de coordenadas destro . Vamos começar com a parte mais simples, esses são os eixos X, Y, porque sua linha muda em apenas uma direção. Após o loop que desenha o cubo (loop de arestas), adicione a renderização do eixo X, Y:const center = new Vector(400, -300, 0)
drawer.drawLine(
center.x, center.y,
center.x, center.y + 200,
150, 150, 150
)
drawer.drawLine(
center.x, center.y,
center.x + 200, center.y,
150, 150, 150
)
O vetor central é o meio da janela de desenho, porque temos as dimensões atuais de 800 por 600 e -300 para Y, indiquei, porque a função drawPixel vira Y e torna sua direção adequada para a tela (na tela, Y olha para baixo). Em seguida, desenhamos 2 eixos usando drawLine, primeiro deslocando Y 200 pixels para cima (final da linha do eixo Y) e depois X 200 pixels para a direita (final da linha do eixo X). Resultado: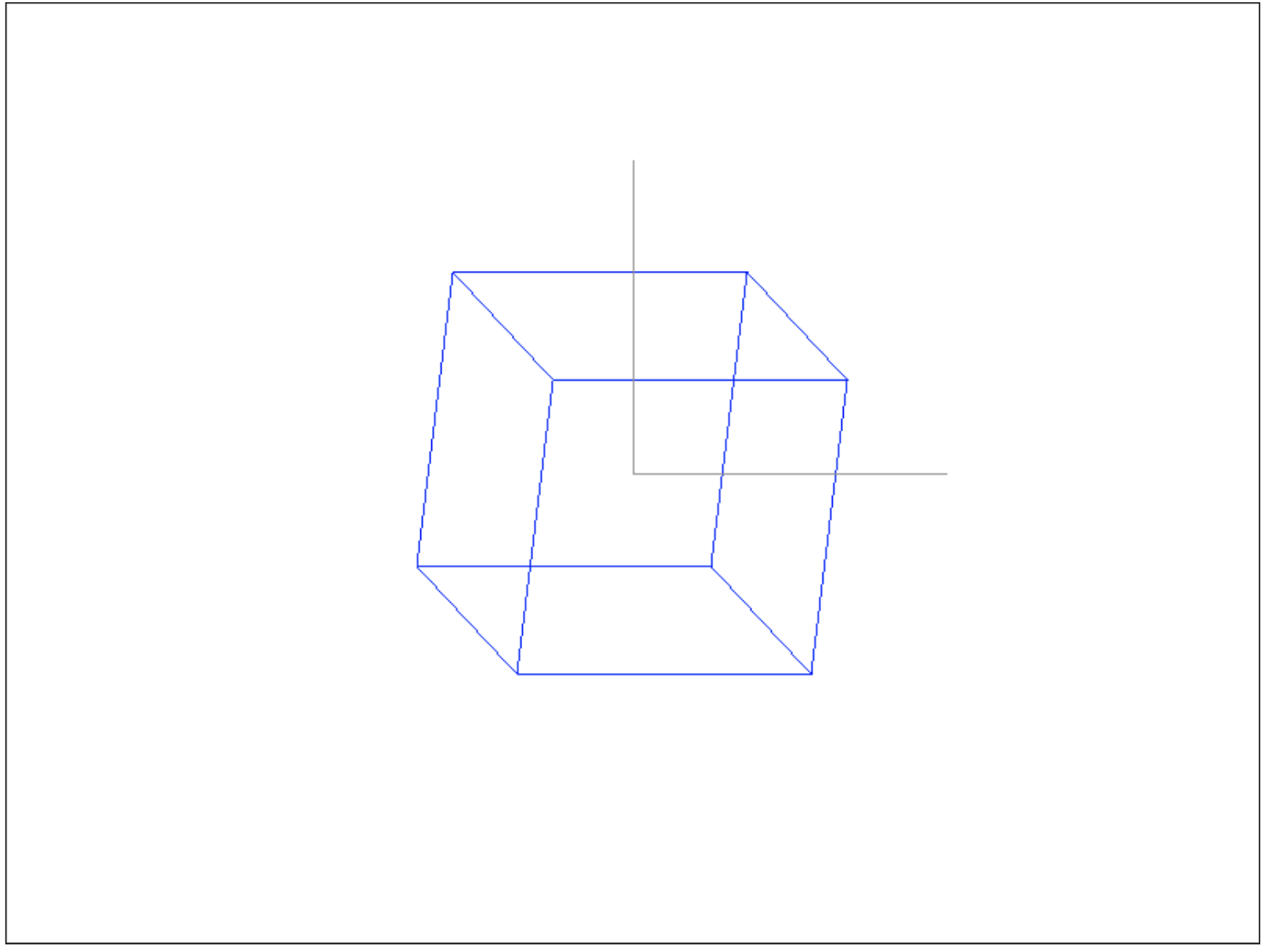
const zVector = new Vector(-1, -1, 0);
const zCoords = Vector.add(
center,
zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
center.x, center.y,
zCoords.x, zCoords.y,
150, 150, 150
);
E, como resultado, você obtém todos os 3 eixos do comprimento desejado:Neste exemplo, o eixo Z mostra apenas qual sistema de coordenadas temos, desenhamos na diagonal para que possa ser visto, porque o eixo Z real é perpendicular ao nosso olhar, e poderíamos desenhá-lo com um ponto na tela, o que não seria bonito.No total, neste artigo, entendemos basicamente os sistemas de coordenadas, vetores e, com algumas operações sobre elas, matrizes e seus papéis nas transformações de coordenadas, classificamos os vértices e escrevemos um transportador simples para visualizar o cubo e os eixos do sistema de coordenadas, fixando a teoria na prática. Todo o código do aplicativo está disponível no spoiler:Código para todo o aplicativoconst ctx = document.getElementById('surface').getContext('2d');
const imageData = ctx.createImageData(800, 600);
class Vector {
x = 0;
y = 0;
z = 0;
w = 1;
constructor(x, y, z, w = 1) {
this.x = x;
this.y = y;
this.z = z;
this.w = w;
}
multiplyByScalar(s) {
this.x *= s;
this.y *= s;
this.z *= s;
return this;
}
static add(v1, v2) {
return new Vector(
v1.x + v2.x,
v1.y + v2.y,
v1.z + v2.z,
);
}
getLength() {
return Math.sqrt(
this.x * this.x + this.y * this.y + this.z * this.z
);
}
normalize() {
const length = this.getLength();
this.x /= length;
this.y /= length;
this.z /= length;
return this;
}
}
class Matrix {
static multiply(a, b) {
const m = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
];
for (let i = 0 ; i < 4 ; i++) {
for(let j = 0 ; j < 4 ; j++) {
m[i][j] = a[i][0] * b[0][j] +
a[i][1] * b[1][j] +
a[i][2] * b[2][j] +
a[i][3] * b[3][j];
}
}
return m;
}
static getRotationX(angle) {
const rad = Math.PI / 180 * angle;
return [
[1, 0, 0, 0],
[0, Math.cos(rad), -Math.sin(rad), 0],
[0, Math.sin(rad), Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationY(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), 0, Math.sin(rad), 0],
[0, 1, 0, 0],
[-Math.sin(rad), 0, Math.cos(rad), 0],
[0, 0, 0, 1],
];
}
static getRotationZ(angle) {
const rad = Math.PI / 180 * angle;
return [
[Math.cos(rad), -Math.sin(rad), 0, 0],
[Math.sin(rad), Math.cos(rad), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
];
}
static getTranslation(dx, dy, dz) {
return [
[1, 0, 0, dx],
[0, 1, 0, dy],
[0, 0, 1, dz],
[0, 0, 0, 1],
];
}
static getScale(sx, sy, sz) {
return [
[sx, 0, 0, 0],
[0, sy, 0, 0],
[0, 0, sz, 0],
[0, 0, 0, 1],
];
}
static multiplyVector(m, v) {
return new Vector(
m[0][0] * v.x + m[0][1] * v.y + m[0][2] * v.z + m[0][3] * v.w,
m[1][0] * v.x + m[1][1] * v.y + m[1][2] * v.z + m[1][3] * v.w,
m[2][0] * v.x + m[2][1] * v.y + m[2][2] * v.z + m[2][3] * v.w,
m[3][0] * v.x + m[3][1] * v.y + m[3][2] * v.z + m[3][3] * v.w,
);
}
}
class Drawer {
surface = null;
width = 0;
height = 0;
constructor(surface, width, height) {
this.surface = surface;
this.width = width;
this.height = height;
}
drawPixel(x, y, r, g, b) {
const offset = (this.width * -y + x) * 4;
if (x >= 0 && x < this.width && -y >= 0 && -y < this.height) {
this.surface[offset] = r;
this.surface[offset + 1] = g;
this.surface[offset + 2] = b;
this.surface[offset + 3] = 255;
}
}
drawLine(x1, y1, x2, y2, r = 0, g = 0, b = 0) {
const round = Math.trunc;
x1 = round(x1);
y1 = round(y1);
x2 = round(x2);
y2 = round(y2);
const c1 = y2 - y1;
const c2 = x2 - x1;
const length = Math.max(
Math.abs(c1),
Math.abs(c2)
);
const xStep = c2 / length;
const yStep = c1 / length;
for (let i = 0 ; i <= length ; i++) {
this.drawPixel(
Math.trunc(x1 + xStep * i),
Math.trunc(y1 + yStep * i),
r, g, b,
);
}
}
clearSurface() {
const surfaceSize = this.width * this.height * 4;
for (let i = 0; i < surfaceSize; i++) {
this.surface[i] = 0;
}
}
}
const drawer = new Drawer(
imageData.data,
imageData.width,
imageData.height
);
const vertices = [
new Vector(-1, 1, 1),
new Vector(-1, 1, -1),
new Vector(1, 1, -1),
new Vector(1, 1, 1),
new Vector(-1, -1, 1),
new Vector(-1, -1, -1),
new Vector(1, -1, -1),
new Vector(1, -1, 1),
];
const edges = [
[0, 1],
[1, 2],
[2, 3],
[3, 0],
[0, 4],
[1, 5],
[2, 6],
[3, 7],
[4, 5],
[5, 6],
[6, 7],
[7, 4],
];
let angle = 0;
setInterval(() => {
let matrix = Matrix.getRotationX(20);
matrix = Matrix.multiply(
Matrix.getRotationY(angle += 1),
matrix
);
matrix = Matrix.multiply(
Matrix.getScale(100, 100, 100),
matrix,
);
matrix = Matrix.multiply(
Matrix.getTranslation(400, -300, 0),
matrix,
);
const sceneVertices = [];
for(let i = 0 ; i < vertices.length ; i++) {
let vertex = Matrix.multiplyVector(
matrix,
vertices[i]
);
sceneVertices.push(vertex);
}
drawer.clearSurface();
for (let i = 0, l = edges.length ; i < l ; i++) {
const e = edges[i];
drawer.drawLine(
sceneVertices[e[0]].x,
sceneVertices[e[0]].y,
sceneVertices[e[1]].x,
sceneVertices[e[1]].y,
0, 0, 255
);
}
const center = new Vector(400, -300, 0)
drawer.drawLine(
center.x, center.y,
center.x, center.y + 200,
150, 150, 150
);
drawer.drawLine(
center.x, center.y,
center.x + 200, center.y,
150, 150, 150
);
const zVector = new Vector(-1, -1, 0, 0);
const zCoords = Vector.add(
center,
zVector.normalize().multiplyByScalar(150)
);
drawer.drawLine(
center.x, center.y,
zCoords.x, zCoords.y,
150, 150, 150
);
ctx.putImageData(imageData, 0, 0);
}, 100);
Qual é o próximo?
Na próxima parte, consideraremos como controlar a câmera e como fazer uma projeção (quanto mais longe o objeto, menor), conhecer os triângulos e descobrir como criar modelos 3D a partir deles, analisar o que são normais e por que são necessários.