Antecipando o início do curso, "Algoritmos para desenvolvedores" preparamos para você uma tradução de outro material útil.
A codificação de Huffman é um algoritmo de compactação de dados que formula a idéia básica da compactação de arquivos. Neste artigo, falaremos sobre codificação de comprimento fixo e variável, códigos decodificados exclusivamente, regras de prefixo e a construção de uma árvore Huffman.Sabemos que cada caractere é armazenado como uma sequência de 0 e 1 e leva 8 bits. Isso é chamado de codificação de comprimento fixo, porque cada caractere usa o mesmo número fixo de bits para armazenar.Digamos que o texto seja dado. Como podemos reduzir a quantidade de espaço necessária para armazenar um personagem?A idéia básica é a codificação de comprimento variável. Podemos usar o fato de que alguns caracteres no texto são mais comuns que outros ( veja aqui ) para desenvolver um algoritmo que representará a mesma sequência de caracteres com menos bits. Ao codificar um comprimento variável, atribuímos um número variável de bits aos caracteres, dependendo da frequência de sua aparência neste texto. Por fim, alguns caracteres podem ocupar apenas 1 bit e outros 2 bits, 3 ou mais. O problema com a codificação de comprimento variável é apenas a decodificação subsequente da sequência.Como, conhecendo a sequência de bits, decodificá-la exclusivamente?Considere a string "aabacdab" . Possui 8 caracteres e, ao codificar um comprimento fixo, serão necessários 64 bits para armazená-lo. Observe que a frequência dos caracteres "a", "b", "c" e "d" é 4, 2, 1, 1, respectivamente. Vamos tentar imaginar "aabacdab" com menos bits, usando o fato de que "a" é mais comum que "b" e "b" é mais comum que "c" e "d" . Para começar, codificamos “a” usando um bit igual a 0, “b” atribuímos um código de dois bits 11 e, usando três bits 100 e 011, codificamos “c” e"D" .Como resultado, teremos sucesso:Assim, codificamos a string "aabacdab" como 00110100011011 (0 | 0 | 11 | 0 | 100 | 011 | 0 | 11) usando os códigos apresentados acima. No entanto, o principal problema será a decodificação. Quando tentamos decodificar a linha 00110100011011 , obtemos um resultado ambíguo, pois pode ser representado como:0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
...etc.Para evitar essa ambiguidade, precisamos garantir que nossa codificação satisfaça um conceito como uma regra de prefixo , o que implica que os códigos podem ser decodificados de uma única maneira. Uma regra de prefixo garante que nenhum código seja um prefixo de outro. Por código, queremos dizer bits usados para representar um caractere específico. No exemplo acima, 0 é o prefixo 011 , que viola a regra do prefixo. Portanto, se nossos códigos atenderem à regra do prefixo, poderemos decodificar exclusivamente (e vice-versa).Vamos revisar o exemplo acima. Desta vez, atribuiremos os caracteres "a", "b", "c" e "d" Códigos que atendem à regra de prefixo.Usando essa codificação, a cadeia “aabacdab” será codificada como 00100100011010 (0 | 0 | 10 | 0 | 100 | 011 | 0 | 10) . E aqui 00100100011010 podemos decodificar e retornar exclusivamente à nossa linha original "aabacdab" .Codificação de Huffman
Agora que descobrimos a codificação de comprimento variável e uma regra de prefixo, vamos falar sobre a codificação de Huffman.O método é baseado na criação de árvores binárias. Nele, um nó pode ser finito ou interno. Inicialmente, todos os nós são considerados folhas (folhas), que representam o próprio símbolo e seu peso (ou seja, a frequência da ocorrência). Nós internos contêm o peso do caractere e se referem a dois nós descendentes. Por concordância geral, o bit "0" representa uma sequência no ramo esquerdo e "1" representa à direita. Em uma árvore completa, existem N folhas e N-1 nós internos. Recomenda-se que, ao construir uma árvore Huffman, caracteres não utilizados sejam descartados para obter códigos de tamanho ideal.Usaremos a fila de prioridade para construir a árvore Huffman, onde o nó com a menor frequência receberá a maior prioridade. As etapas de construção são descritas abaixo:- Crie um nó folha para cada caractere e adicione-os à fila de prioridade.
- Enquanto estiver na fila por mais de uma planilha, faça o seguinte:
- Remova os dois nós com a maior prioridade (com a menor frequência) da fila;
- Crie um novo nó interno no qual esses dois nós serão herdeiros e a frequência de ocorrência será igual à soma das frequências desses dois nós.
- Adicione um novo nó à fila de prioridade.
- O único nó restante será a raiz; isso terminará a construção da árvore.
Imagine que temos um texto que consiste apenas nos caracteres "a", "b", "c", "d" e "e" e as frequências de sua aparência são 15, 7, 6, 6 e 5, respectivamente. Abaixo estão ilustrações que refletem as etapas do algoritmo.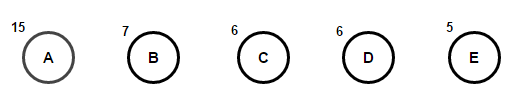
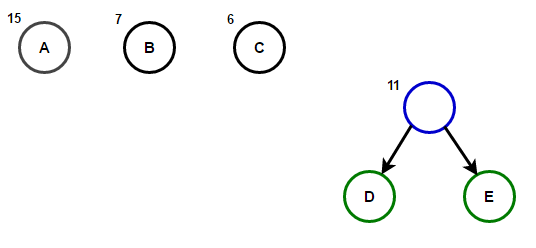
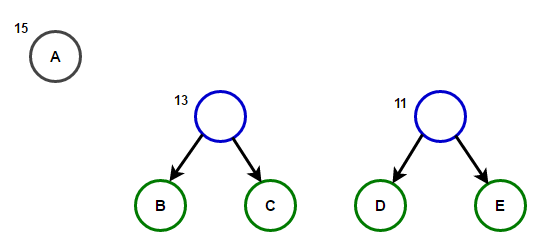
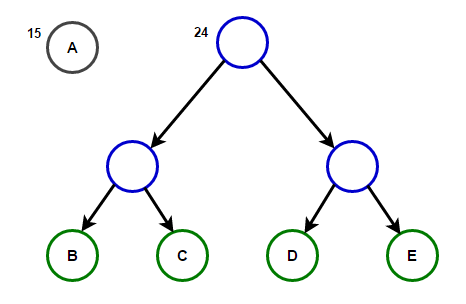
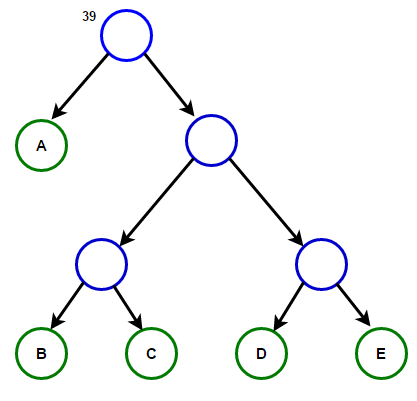 O caminho da raiz para qualquer nó final armazenará o código do prefixo ideal (também conhecido como código Huffman) correspondente ao caractere associado a esse nó final.
O caminho da raiz para qualquer nó final armazenará o código do prefixo ideal (também conhecido como código Huffman) correspondente ao caractere associado a esse nó final.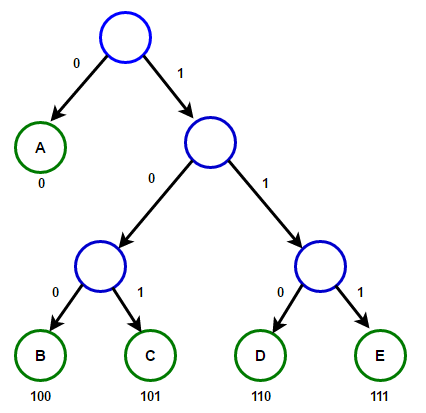 Árvore HuffmanAbaixo, você encontrará a implementação do algoritmo de compactação Huffman em C ++ e Java:
Árvore HuffmanAbaixo, você encontrará a implementação do algoritmo de compactação Huffman em C ++ e Java:#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
struct Node
{
char ch;
int freq;
Node *left, *right;
};
Node* getNode(char ch, int freq, Node* left, Node* right)
{
Node* node = new Node();
node->ch = ch;
node->freq = freq;
node->left = left;
node->right = right;
return node;
}
struct comp
{
bool operator()(Node* l, Node* r)
{
return l->freq > r->freq;
}
};
void encode(Node* root, string str,
unordered_map<char, string> &huffmanCode)
{
if (root == nullptr)
return;
if (!root->left && !root->right) {
huffmanCode[root->ch] = str;
}
encode(root->left, str + "0", huffmanCode);
encode(root->right, str + "1", huffmanCode);
}
void decode(Node* root, int &index, string str)
{
if (root == nullptr) {
return;
}
if (!root->left && !root->right)
{
cout << root->ch;
return;
}
index++;
if (str[index] =='0')
decode(root->left, index, str);
else
decode(root->right, index, str);
}
void buildHuffmanTree(string text)
{
unordered_map<char, int> freq;
for (char ch: text) {
freq[ch]++;
}
priority_queue<Node*, vector<Node*>, comp> pq;
for (auto pair: freq) {
pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
}
while (pq.size() != 1)
{
Node *left = pq.top(); pq.pop();
Node *right = pq.top(); pq.pop();
int sum = left->freq + right->freq;
pq.push(getNode('\0', sum, left, right));
}
Node* root = pq.top();
unordered_map<char, string> huffmanCode;
encode(root, "", huffmanCode);
cout << "Huffman Codes are :\n" << '\n';
for (auto pair: huffmanCode) {
cout << pair.first << " " << pair.second << '\n';
}
cout << "\nOriginal string was :\n" << text << '\n';
string str = "";
for (char ch: text) {
str += huffmanCode[ch];
}
cout << "\nEncoded string is :\n" << str << '\n';
int index = -1;
cout << "\nDecoded string is: \n";
while (index < (int)str.size() - 2) {
decode(root, index, str);
}
}
int main()
{
string text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
return 0;
}
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class Node
{
char ch;
int freq;
Node left = null, right = null;
Node(char ch, int freq)
{
this.ch = ch;
this.freq = freq;
}
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
};
class Huffman
{
public static void encode(Node root, String str,
Map<Character, String> huffmanCode)
{
if (root == null)
return;
if (root.left == null && root.right == null) {
huffmanCode.put(root.ch, str);
}
encode(root.left, str + "0", huffmanCode);
encode(root.right, str + "1", huffmanCode);
}
public static int decode(Node root, int index, StringBuilder sb)
{
if (root == null)
return index;
if (root.left == null && root.right == null)
{
System.out.print(root.ch);
return index;
}
index++;
if (sb.charAt(index) == '0')
index = decode(root.left, index, sb);
else
index = decode(root.right, index, sb);
return index;
}
public static void buildHuffmanTree(String text)
{
Map<Character, Integer> freq = new HashMap<>();
for (int i = 0 ; i < text.length(); i++) {
if (!freq.containsKey(text.charAt(i))) {
freq.put(text.charAt(i), 0);
}
freq.put(text.charAt(i), freq.get(text.charAt(i)) + 1);
}
PriorityQueue<Node> pq = new PriorityQueue<>(
(l, r) -> l.freq - r.freq);
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
pq.add(new Node(entry.getKey(), entry.getValue()));
}
while (pq.size() != 1)
{
Node left = pq.poll();
Node right = pq.poll();
int sum = left.freq + right.freq;
pq.add(new Node('\0', sum, left, right));
}
Node root = pq.peek();
Map<Character, String> huffmanCode = new HashMap<>();
encode(root, "", huffmanCode);
System.out.println("Huffman Codes are :\n");
for (Map.Entry<Character, String> entry : huffmanCode.entrySet()) {
System.out.println(entry.getKey() + " " + entry.getValue());
}
System.out.println("\nOriginal string was :\n" + text);
StringBuilder sb = new StringBuilder();
for (int i = 0 ; i < text.length(); i++) {
sb.append(huffmanCode.get(text.charAt(i)));
}
System.out.println("\nEncoded string is :\n" + sb);
int index = -1;
System.out.println("\nDecoded string is: \n");
while (index < sb.length() - 2) {
index = decode(root, index, sb);
}
}
public static void main(String[] args)
{
String text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
}
}
Nota: a memória usada pela sequência de entrada é 47 * 8 = 376 bits, e a sequência codificada leva apenas 194 bits, ou seja, os dados são compactados em cerca de 48%. No programa C ++ acima, usamos a classe string para armazenar a string codificada para tornar o programa legível.Como estruturas de dados efetivas da fila de prioridade exigem tempo O (log (N)) para serem inseridas, e em uma árvore binária completa com N folhas existem 2N-1 nós, e a árvore Huffman é uma árvore binária completa, o algoritmo funciona para O (Nlog (N )) hora, onde N é o número de caracteres.Fontes:
en.wikipedia.org/wiki/Huffman_codingen.wikipedia.org/wiki/Variable-length_codewww.youtube.com/watch?v=5wRPin4oxCo
.