Isso soa familiar: "Comecei a desenvolver web depois de fazer cursos"?Talvez você queira melhorar seu conhecimento dos conceitos básicos de ciência da computação em termos de estruturas de dados e algoritmos. Hoje falaremos sobre algumas das estruturas de dados mais comuns usando o exemplo JS.1. Pilha (chamadas) (Pilha)
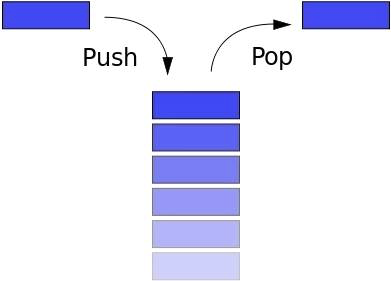A pilha segue o princípio LIFO (Last In First Out - Last In, First Out). Se você empilhou os livros um sobre o outro e queria pegar o livro mais baixo, primeiro pegue o livro de cima, depois o próximo, etc. O botão "Voltar" no navegador permite que você volte (retorne) à página anterior.A pilha possui os seguintes métodos:- push: adicionar novo item
- pop: remova o elemento superior, retorne-o
- peek: retornar elemento superior
- length: retorna o número de elementos na pilha
Uma matriz em JS possui atributos de pilha, mas a construiremos do zero usando a função Stack ():function Stack() {
this.count = 0
this.storage = {}
this.push = function(value) {
this.storage[this.count] = value
this.count++
}
this.pop = function() {
if (this.count === 0) return undefined
this.count--
let result = this.storage[this.count]
delete this.storage[this.count]
return result
}
this.peek = function() {
return this.storage[this.count - 1]
}
this.size = function() {
return this.count
}
}
2. Fila (Fila)
Uma fila se parece com uma pilha. A diferença é que a fila segue o princípio FIFO (primeiro a entrar, primeiro a entrar, primeiro a sair). Quando você fica na fila, o primeiro sempre será o primeiro.A fila possui os seguintes métodos:- enfileirar: entre na fila, adicione um item ao final
- desenfileirar: saia da fila, exclua o primeiro elemento e retorne-o
- front: obtenha o primeiro elemento
- isEmpty: verifique se a fila está vazia
- size: obtém o número de itens na fila
Uma matriz em JS possui alguns atributos de fila, para que possamos usá-la para demonstração:function Queue() {
let collection = []
this.print = function() {
console.log(collection)
}
this.enqueue = function(element) {
collection.push(element)
}
this.dequeue = function() {
return collection.shift()
}
this.front = function() {
return collection[0]
}
this.isEmpty = function() {
return collection.length === 0
}
this.size = function() {
return collection.length
}
}
A ordem da prioridade (prioridade)
A fila tem uma versão avançada. Atribua a cada item uma prioridade e os itens serão classificados de acordo:function PriorityQueue() {
...
this.enqueue = function(element) {
if (this.isEmpty()) {
collection.push(element)
} else {
let added = false
for (let i = 0; i < collection.length; i++) {
if (element[1] < collection[i][1]) {
collection.splice(i, 0, element)
added = true
break;
}
}
if (!added) {
collection.push(element)
}
}
}
}
Teste:let pQ = new PriorityQueue()
pQ.enqueue([gannicus, 3])
pQ.enqueue([spartacus, 1])
pQ.enqueue([crixus, 2])
pQ.enqueue([oenomaus, 4])
pQ.print()
Resultado:[
[spartacus, 1],
[crixus, 2],
[gannicus, 3],
[oenomaus, 4]
]
3. Uma lista vinculada (lista vinculada de nós e links ou ponteiros) (Lista vinculada)
Literalmente, uma lista vinculada é uma estrutura de dados encadeada, em que cada nó consiste em duas partes: dados do nó e um ponteiro para o próximo nó. A lista vinculada e a matriz condicional são estruturas de dados lineares com armazenamento serializado. As diferenças são as seguintes:Uma lista vinculada individualmente possui os seguintes métodos:- tamanho: retorna o número de nós
- head: retorna o primeiro elemento (head - head)
- add: adiciona um elemento ao final (tail - tail)
- remover: remover vários nós
- indexOf: índice do nó de retorno
- elementAt: retornar nó por índice
- addAt: insere um nó em um local específico (por índice)
- removeAt: remove um nó específico (por índice)
function Node(element) {
this.element = element
this.next = null
}
function LinkedList() {
let length = 0
let head = null
this.size = function() {
return length
}
this.head = function() {
return head
}
this.add = function(element) {
let node = new Node(element)
if (head === null) {
head = node
} else {
let currentNode = head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = node
}
length++
}
this.remove = function(element) {
let currentNode = head
let previousNode
if (currentNode.element !== element) {
head = currentNode.next
} else {
while (currentNode.element !== element) {
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
}
this.isEmpty = function() {
return length === 0
}
this.indexOf = function(element) {
let currentNode = head
let index = -1
while (currentNode) {
index++
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
}
return -1
}
this.elementAt = function(index) {
let currentNode = head
let count = 0
while (count < index) {
count++
currentNode = currentNode.next
}
return currentNode.element
}
this.addAt = function(index, element) {
let node = new Node(element)
let currentNode = head
let previousNode
let currentIndex = 0
if (index > length) return false
if (index === 0) {
node.next = currentNode
head = node
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
node.next = currentNode
previousNode.next = node
}
length++
}
this.removeAt = function(index) {
let currentNode = head
let previousNode
let currentIndex = 0
if (index < 0 || index >= length) return null
if (index === 0) {
head = currentIndex.next
} else {
while (currentIndex < index) {
currentIndex++
previousNode = currentNode
currentNode = currentNode.next
}
previousNode.next = currentNode.next
}
length--
return currentNode.element
}
}
4. Coleta (de valores) (Conjunto)
Uma coleção (muitos) é um dos conceitos básicos da matemática: um conjunto de objetos bem definidos e isolados. O ES6 introduziu uma coleção que tem alguma semelhança com uma matriz. No entanto, a coleção não permite a inclusão de elementos duplicados e não contém índices.A coleção padrão possui os seguintes métodos:- valores: retorna todos os itens da coleção
- tamanho: retorna o número de elementos
- has: verifique se um item está na coleção
- add: adicionar item
- remover: remover um item
- união: retorna a área de interseção de duas coleções
- diferença: retorna as diferenças entre as duas coleções
- subconjunto: verifique se uma coleção é um subconjunto de outra
function MySet() {
let collection = []
this.has = function(element) {
return (collection.indexOf(element) !== -1)
}
this.values = function() {
return collection
}
this.size = function() {
return collection.length
}
this.add = function(element) {
if (!this.has(element)) {
collection.push(element)
return true
}
return false
}
this.remove = function(element) {
if (this.has(element)) {
index = collection.indexOf(element)
collection.splice(index, 1)
return true
}
return false
}
this.union = function(otherSet) {
let unionSet = new MySet()
let firstSet = this.values()
let secondSet = otherSet.values()
firstSet.forEach(i => unionSet.add(i))
secondSet.forEach(i => unionSet.add(i))
}
this.intersection = function(otherSet) {
let intersectionSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (otherSet.has(e)) {
intersectionSet.add(e)
}
})
return intersectionSet
}
this.difference = function(otherSet) {
let differenceSet = new MySet()
let firstSet = this.values()
firstSet.forEach(function(e) {
if (!otherSet.has(e)) {
differenceSet.add(e)
}
})
return differenceSet
}
this.subset = function(otherSet) {
lat firstSet = this.values()
return firstSet.every(value => otherSet.has(value))
}
}
5. Tabela de Hash (Tabela de Hash)
Uma tabela de hash é uma estrutura de dados criada com base em valores-chave. Devido à alta velocidade de busca de valores por chave, é usado em estruturas como Mapa, Dicionário e Objeto. Conforme mostrado na figura, a tabela de hash possui uma função de hash que converte chaves em uma lista de números usados como nomes (valores) de chaves. O tempo de busca do valor-chave pode chegar a O (1). Chaves idênticas devem retornar o mesmo valor - essa é a essência da função hash.Uma tabela de hash possui os seguintes métodos:- add: adiciona um par de chave / valor
- remover: remover um par
- pesquisa: encontre valor por chave
function hash(string, max) {
let hash = 0
for (let i = 0; i < string.length; i++) {
hash += string.charCodeAt(i)
}
return hash % max
}
function HashTable() {
let storage = []
const storageLimit = 4
this.add = function(key, value) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
storage[index] = [
[key, value]
]
} else {
let inserted = false
for (let i = 0; i < storage[index].len; i++) {
if (storage[index][i][0] === key) {
storage[index][i][1] = value
inserted = true
}
}
if (inserted === false) {
storage[index].push([key, value])
}
}
}
this.remove = function(key) {
let index = hash(key, storageLimit)
if (storage[index].length === 1 && storage[index][0][0] === key) {
delete storage[index]
} else {
for (let i = 0; i < storage[index]; i++) {
if (storage[index][i][0] === key) {
delete storage[index][i]
}
}
}
}
this.lookup = function(key) {
let index = hash(key, storageLimit)
if (storage[index] === undefined) {
return undefined
} else {
for (let i = 0; i < storage[index].length; i++) {
if (storage[index][i][0] === key) {
return storage[index][i][1]
}
}
}
}
}
6. Árvore
Uma estrutura em árvore é uma estrutura multicamada (multinível). Também é uma estrutura não linear, diferente de uma matriz, pilha e fila. Essa estrutura é muito eficaz em termos de adição e pesquisa de elementos. Aqui estão alguns conceitos de estrutura de árvore:- root: elemento raiz, não tem pai
- nó pai: um nó direto da camada superior (nível), pode haver apenas um
- nó filho: nó (s) direto (s) do nível inferior, pode haver vários
- irmãos: filhos de um nó pai
- folha: nó sem "filhos"
- Borda: ramificação ou link (link) entre nós
- Caminho: caminho (conjunto de links) do nó inicial ao elemento de destino
- Height of Tree: o número de links do caminho mais longo de um elemento específico para um nó que não tem filhos
- Profundidade do nó: o número de links do nó raiz para um elemento específico.
- Grau de nó: Número de descendentes
Aqui está um exemplo de uma árvore de pesquisa binária (BST). Cada nó possui apenas dois descendentes, o nó esquerdo (filho) é menor que o nó atual (pai) e o direito é maior: Os
métodos dessa árvore são os seguintes:- add: adicionar nó
- findMin: obtenha o nó mínimo
- findMax: obtenha o nó máximo
- find: encontra um nó específico
- isPresent: verifique se há um nó específico
- remover: remover o nó
class Node {
constructor(data, left = null, right = null) {
this.data = data
this.left = left
this.right = right
}
}
class BST {
constructor() {
this.root = null
}
add(data) {
const node = this.root
if (node === null) {
this.root = new Node(data)
return
} else {
const searchTree = function(node) {
if (data < node.data) {
if (node.left === null) {
node.left = new Node(data)
return
} else if (node.left !== null) {
return searchTree(node.left)
}
} else if (data > node.data) {
if (node.right === null) {
node.right = new Node(data)
return
} else if (node.right !== null) {
return searchTree(node.right)
}
} else {
return null
}
}
return searchTree(node)
}
}
findMin() {
let current = this.root
while (current.left !== null) {
current = current.left
}
return current.data
}
findMax() {
let current = this.root
while (current.right !== null) {
current = current.right
}
return current.data
}
find(data) {
let current = this.root
while (current.data !== data) {
if (data < current.data) {
current = current.left
} else {
current = current.right
}
if (current === null) {
return null
}
}
return current
}
isPresent(data) {
let current = this.root
while (current) {
if (data === current.data) {
return true
}
data < current.data ? current = current.left : current = current.right
}
return false
}
remove(data) {
const removeNode = function(node, data) {
if (node === null) return null
if (data === node.data) {
if (node.left === null && node.right === null) return null
if (node.left === null) return node.right
if (node.right === null) return node.left
let tempNode = node.right
while (tempNode.left !== null) {
tempNode = tempNode.left
}
node.data = tempNode.data
node.right = removeNode(node.right, tempNode.data)
return node
} else if (data < node.data) {
node.left = removeNode(node.right, data)
return node
} else {
node.right = removeNode(node.right, data)
return node
}
}
this.root = removeNode(this.root, data)
}
}
Teste:const bst = new BST()
bst.add(4)
bst.add(2)
bst.add(6)
bst.add(1)
bst.add(3)
bst.add(5)
bst.add(7)
bst.remove(4)
console.log(bst.findMin())
console.log(bst.findMax())
bst.remove(7)
console.log(bst.findMax())
console.log(bst.isPresent(4))
Resultado:1
7
6
false
7. Árvore carregada (prefixo) (Trie, leia como “try”)
A árvore de prefixos é um tipo de árvore de pesquisa. Os dados nele são armazenados sequencialmente (passo a passo) - cada nó da árvore representa um passo. A árvore de prefixos é usada nos dicionários, pois acelera significativamente a pesquisa.Cada nó da árvore é uma letra do alfabeto, após um ramo leva à formação de uma palavra. Ele também contém um "indicador booleano" para determinar que o nó atual é a última letra.A árvore de prefixos possui os seguintes métodos:- add: adiciona uma palavra ao dicionário
- isWord: verifique uma palavra
- print: retorna todas as palavras
function Node() {
this.keys = new Map()
this.end = false
this.setEnd = function() {
this.end = true
}
this.isEnd = function() {
return this.end
}
}
function Trie() {
this.root = new Node()
this.add = function(input, node = this.root) {
if (input.length === 0) {
node.setEnd()
return
} else if (!node.keys.has(input[0])) {
node.keys.set(input[0], new Node())
return this.add(input.substr(1), node.key.get(input[0]))
} else {
return this.add(input.substr(1), node.keys.get(input[0]))
}
}
this.isWord = function(word) {
let node = this.root
while (word.length > 1) {
if (node.keys.has(word[0])) {
return false
} else {
node = node.keys.get(word[0])
word = word.substr(1)
}
}
return (node.keys.has(word) && node.keys.get(word).isEnd()) ? true : false
}
this.print = function() {
let words = new Array()
let search = function(node = this.root, string) {
if (node.keys.size !== 0) {
for (let letter of node.keys.keys()) {
search(node.keys.get(letter), string.concat(letter))
}
if (node.isEnd()) {
words.push(string)
}
} else {
string.length > 0 ? words.push(string) : undefined
return
}
}
search(this.root, new String())
return words.length > 0 ? words : null
}
}
8. O gráfico (gráfico) (gráfico)
Um gráfico, também conhecido como rede, é uma coleção de nós interconectados. Existem dois tipos de gráficos - orientados e não orientados, dependendo se os links têm uma direção. Os gráficos são usados em todos os lugares, por exemplo, para calcular a melhor rota em aplicativos de navegação ou para criar uma lista de recomendações nas redes sociais.Os gráficos podem ser apresentados na forma de uma lista ou matriz.Lista
Nesse caso, todos os nós pais estão localizados à esquerda e seus filhos estão à direita.
O Matrix
Nesse caso, os nós são distribuídos em linhas e colunas, a interseção das linhas e colunas mostra a relação entre os nós: 0 significa que os nós não estão conectados, 1 - os nós estão conectados.
O gráfico é pesquisado por dois métodos - pesquisa de primeira largura (Breath-First-Search, BFS) e pesquisa profunda (Depth-First-Search, DFS).Considere o BFS:function bfs(graph, root) {
let nodesLen = {}
for (let i = 0; i < graph.length; i++) {
nodesLen[i] = Infinity
}
nodesLen[root] = 0
let queue = [root]
let current
while (queue.length !== 0) {
current = queue.shift()
let curConnected = graph[current]
let neighborIdx = []
let idx = curConnected.indexOf(1)
while (idx !== -1) {
neighborIdx.push(idx)
idx = curConnected.indexOf(1, idx + 1)
}
for (let i = 0; i < neighborIdx.length; i++) {
if (nodesLen[neighborIdx[i]] === Infinity) {
nodesLen[neighborIdx[i]] = nodesLen[current] + 1
queue.push(neighborIdx[i])
}
}
}
return nodesLen
}
Teste:let graph = [
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[1, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 0, 0]
]
console.log(bfs(graph, 1))
Resultado:{
0: 2,
1: 0,
2: 1,
3: 3,
4: Infinity
}
Isso é tudo para mim. Espero que você encontre algo útil para si mesmo. Feliz codificação!