👏 🍆 👶🏽 Algoritmo de propagação de erro de volta usando o Word2Vec como exemplo 🕴🏿 🎪 💡

Como encontrei dificuldades significativas em encontrar uma explicação do mecanismo de propagação de retorno do erro que gostaria, decidi escrever meu próprio post sobre a propagação de retorno do erro usando o algoritmo Word2Vec. Meu objetivo é explicar a essência do algoritmo usando uma rede neural simples, mas não trivial. Além disso, o word2vec se tornou tão popular na comunidade da PNL que será útil se concentrar nele.

Este post está conectado a outro post mais prático que eu recomendo a leitura, que discute a implementação direta do word2vec em python. Neste post, focaremos principalmente a parte teórica.

Vamos começar com as coisas necessárias para uma verdadeira compreensão da retropropagação. Além dos conceitos de aprendizado de máquina, como a função de perda e a descida em gradiente, mais dois componentes da matemática são úteis:

álgebra linear (em particular multiplicação de matrizes)
regra da cadeia de diferenciação de funções de muitas variáveis

Se você estiver familiarizado com esses conceitos, outras considerações serão simples. Se você ainda não os domina, ainda pode entender o básico da retropropagação.

Primeiro, quero definir o conceito de propagação reversa, se o significado não for suficientemente claro, será divulgado com mais detalhes nos parágrafos seguintes.

1. O que é um algoritmo de retropropagação?

, , , ( , ). , .

, — , , .
, , .
, , , , w1 w2.

1. .

, w1 w2 .

, . , $\partial\mathcal{L}/\partial w_1$ $\partial\mathcal{L}/\partial w_2$ , , . $\eta$ , .

2. Word2Vec

word2vec, , , . , word2vec, NLP.

, word2vec [N, 3], N - , . , , '', , ( ), , ''. , word2vec .

word2vec : (CBOW) (skip-gram). , CBOW, , skip-gram.

. , woed2vec .

3. CBOW

CBOW . , :

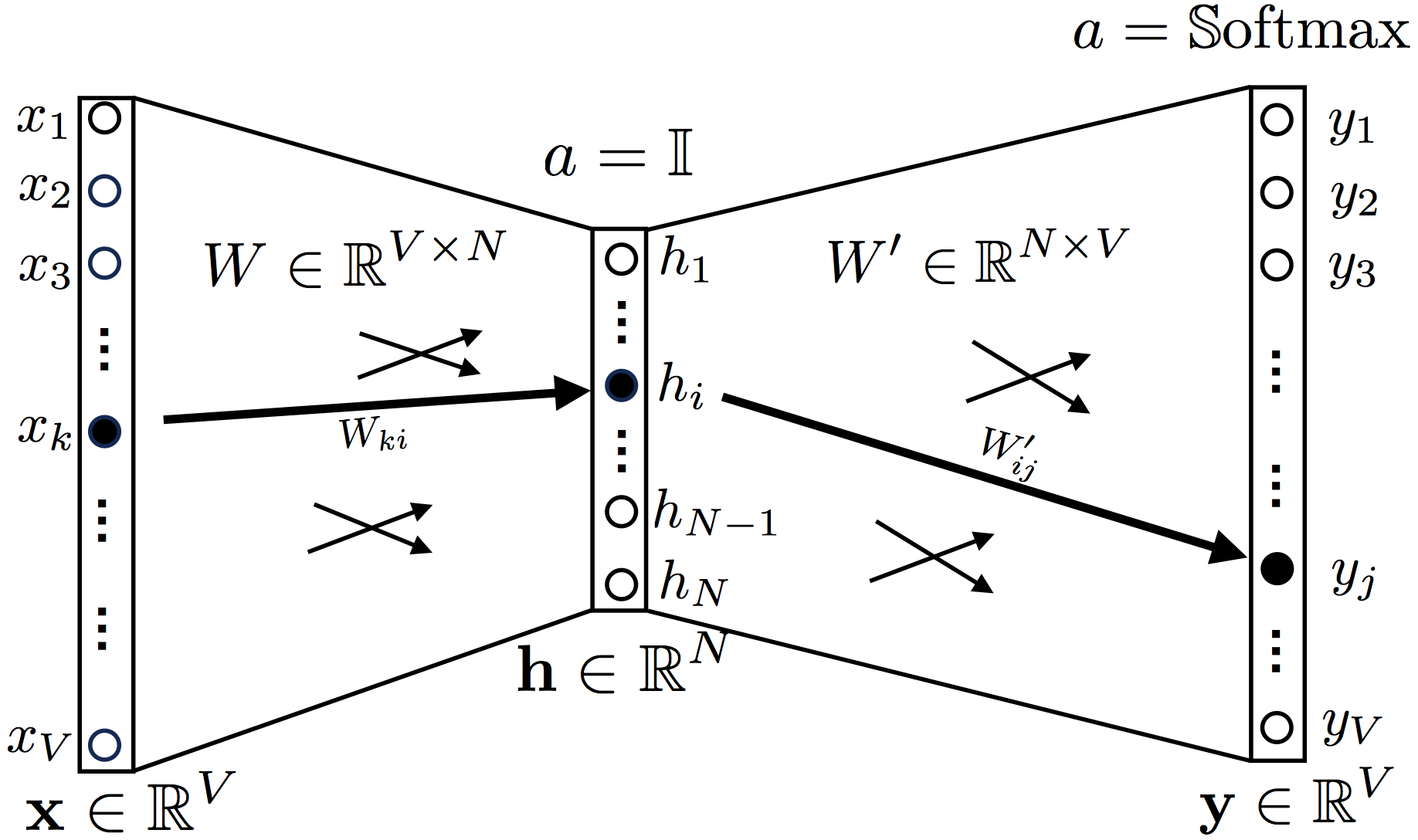
2. Continuous Bag-of-Words

, ,
a = 1 (identity function, , ).
Softmax.

one hot encoding , , , , , 1.

: ['', '', '', '', '', '']
OneHot('') = [0, 0, 0, 1, 0, 0]
OneHot(['', '']) = [1, 0, 0, 1, 0, 0]
OneHot(['', '', '']) = [1, 0, 0, 0, 1, 1]

, W $V\times N$ , $W’$ $N\times V$ , V — , N — ( , word2vec)

y t, , , , , .

, .

, word2vec :
"I like playing football"
CBOW (2) .
, 4 , V=4, , N=2, :

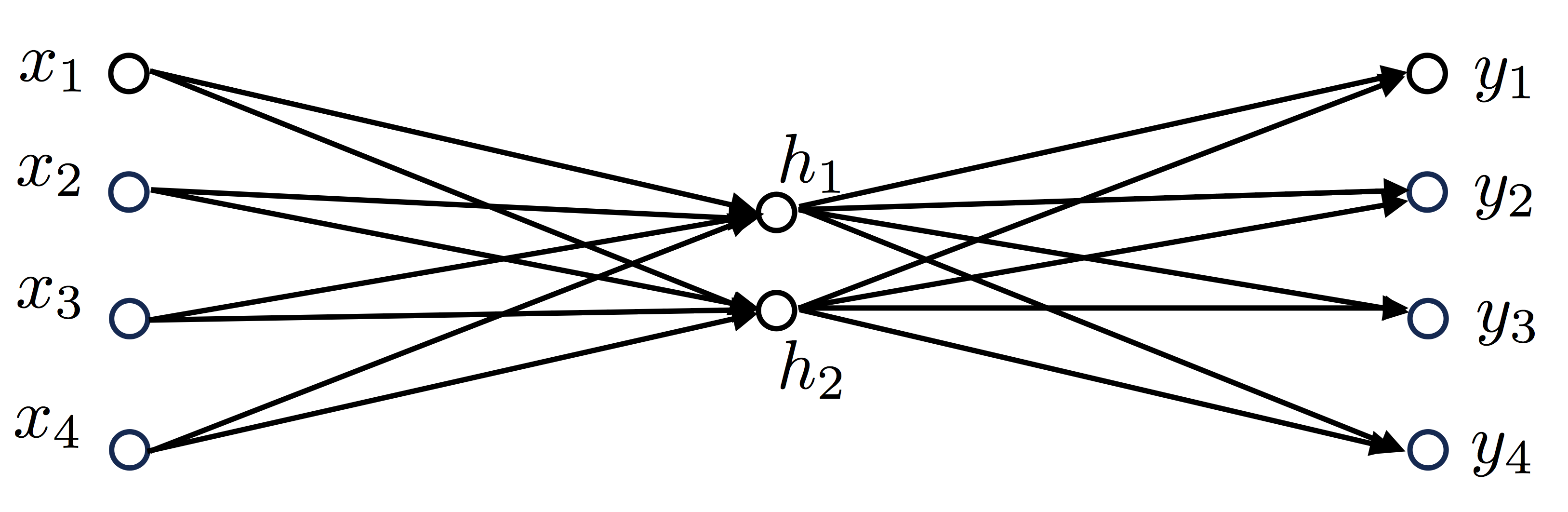
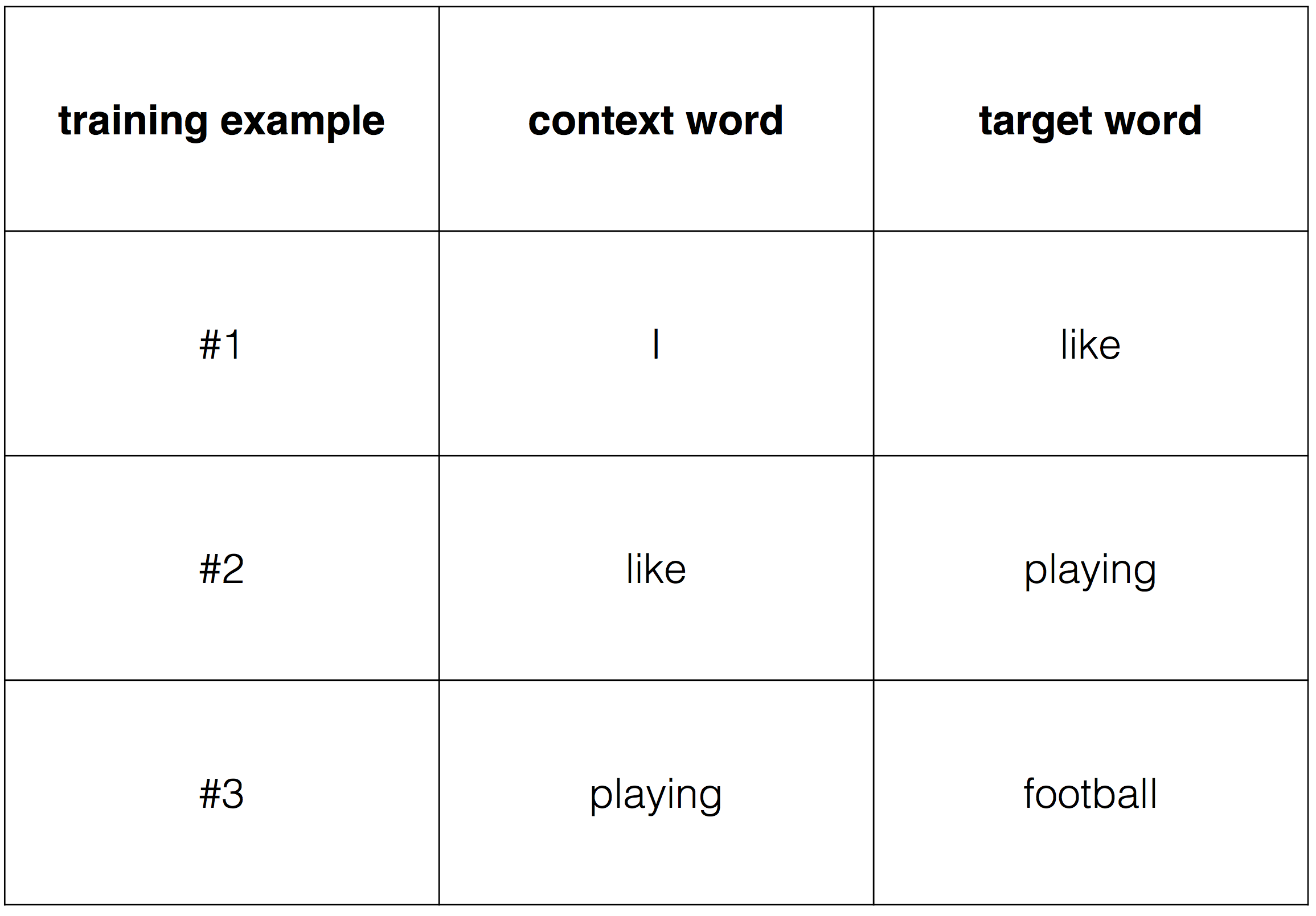
Vocabulary = [“I”, “like”, “playing”, “football”]

$\textrm{Vocabulary}=[\textrm{“I”}, \textrm{“like”}, \textrm{“playing”}, \textrm{“football”}]$

'' '' , . :

, one-hot encoding.

, , , . , , .

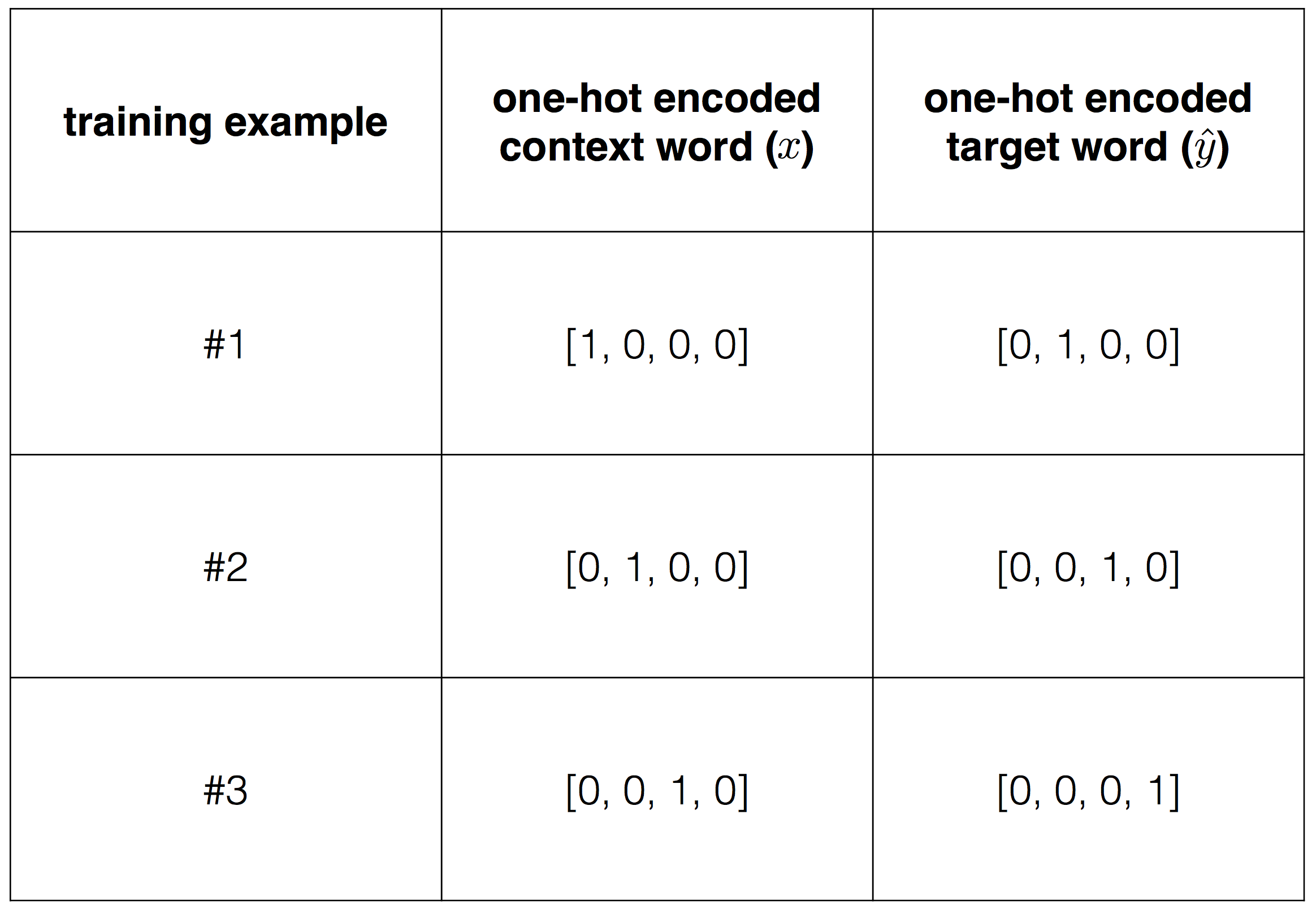
3.1 (Loss function)

1, , x:

\begin{array}{rcl} h = & W^{T} x \\ u = & W^{' T} h = W^{' T} W^{T} x \\ y = & S oftmax (u) = S oftmax (W^{' T} W^{T} x) \end{array}

$\begin{eqnarray*} \textbf{h} = & W^T\textbf{x} \hspace{7.0cm} \\ \textbf{u}= & W'^T\textbf{h}=W'^TW^T\textbf{x} \hspace{4.6cm} \\ \textbf{y}= & \ \ \mathbb{S}\textrm{oftmax}(\textbf{u})= \mathbb{S}\textrm{oftmax}(W'^TW^T\textbf{x}) \hspace{2cm} \end{eqnarray*}$

, h — , u — , y — .

, , , (wt, wc). , onehot encoding .

, onehot wt ( ).

softmax , :

L = - \log P (w_{t} | w_{c}) = - \log y_{j^{*}} = - \log [S oftmax (u_{j^{*}})] = - \log (\frac{\exp u_{j^{*}}}{\sum_{i} \exp u_{i}}),

$\begin{equation*} \mathcal{L} = -\log \mathbb{P}(w_t|w_c)=-\log y_{j^*}\ =-\log[\mathbb{S}\textrm{oftmax}(u_{j^*})]=-\log\left(\frac{\exp{u_{j^*}}}{\sum_i \exp{u_i}}\right), \end{equation*}$

, j* — .
. (1):

L = - u_{j^{*}} + \log \sum_{i} \exp (u_{i}) . (1)

$\begin{equation} \bbox[lightblue,5px,border:2px solid red]{ \mathcal{L} = -u_{j^*} + \log \sum_i \exp{(u_i)}. } \label{eq:loss} \end{equation} \>(1)$

"I like play football", , "I" "like", , $\textbf{x}=(1, 0, 0, 0)$ — "I", $\hat{\textbf{y}}=(0, 1, 0, 0)$ , "like".

word2vec, . W $4\times 2$

W = (\begin{matrix} - 1.38118728 & 0.54849373 \\ 0.39389902 & - 1.1501331 \\ - 1.16967628 & 0.36078022 \\ 0.06676289 & - 0.14292845 \end{matrix})

$W = \begin{pmatrix} -1.38118728 & 0.54849373 \\ 0.39389902 & -1.1501331 \\ -1.16967628 & 0.36078022 \\ 0.06676289 & -0.14292845 \end{pmatrix}$

$W’$ $2\times 4$

W^{'} = (\begin{matrix} 1.39420129 & - 0.89441757 & 0.99869667 & 0.44447037 \\ 0.69671796 & - 0.23364341 & 0.21975196 & - 0.0022673 \end{matrix})

$W' = \begin{pmatrix} 1.39420129 & -0.89441757 & 0.99869667 & 0.44447037 \\ 0.69671796 & -0.23364341 & 0.21975196 & -0.0022673 \end{pmatrix}$

"I like" :

h = W^{T} x = (\begin{matrix} - 1.38118728 \\ 0.54849373 \end{matrix})

$\textbf{h} = W^T\textbf{x}= \begin{pmatrix} -1.38118728 \\ 0.54849373 \end{pmatrix}$

u = W^{' T} h = (\begin{matrix} - 1.54350765 \\ 1.10720623 \\ - 1.25885456 \\ - 0.61514042 \end{matrix})

$\textbf{u} = W'^T\textbf{h}= \begin{pmatrix} -1.54350765 \\ 1.10720623 \\ -1.25885456 \\ -0.61514042 \end{pmatrix}$

y = S oftmax (u) = (\begin{matrix} 0.05256567 \\ 0.7445479 \\ 0.06987559 \\ 0.13301083 \end{matrix})

$\textbf{y} = \mathbb{S}\textrm{oftmax}(\textbf{u})= \begin{pmatrix} 0.05256567 \\ 0.7445479 \\ 0.06987559 \\ 0.13301083 \end{pmatrix}$

$\textbf{y}$ ,

L = - \log P (“like” | “I”) = - \log y_{3} = - \log (0.7445479) = 0.2949781.

$\mathcal{L}=-\log\mathbb{P}(\textrm{“like”}|\textrm{“I”})=-\log y_3 = -\log(0.7445479)= 0.2949781.$

, (1):

\begin{array}{rcl} L = - u_{2} + \log \sum_{i = 1}^{4} u_{i} = - 1.10720623 + \log [\exp (- 1.54350765) + \exp (1.10720623) \\ + \exp (- 1.25885456) + \exp (- 0.61514042)] = 0.2949781. \end{array}

$\begin{eqnarray*} \mathcal{L}=-u_2+\log\sum_{i=1}^4 u_i=-1.10720623 + \log[\exp(-1.54350765)+\exp(1.10720623) \\ +\exp(-1.25885456)+\exp(-0.61514042)]=0.2949781. \end{eqnarray*}$

, "like play", , .

3.2 CBOW

, , W W` . , .

. (1) W W`. $\partial \mathcal{L}/\partial{W}$ $\partial \mathcal{L}/\partial{W’}$

, . (1) W W`, u=[u1, ...., uV],

L = L (u (W, W^{'})) = L (u_{1} (W, W^{'}), u_{2} (W, W^{'}), \dots, u_{V} (W, W^{'})) .

$\begin{equation*} \mathcal{L} = \mathcal{L}(\mathbf{u}(W,W'))=\mathcal{L}(u_1(W,W'), u_2(W,W'),\dots, u_V(W,W'))\ . \end{equation*}$

\frac{\partial L}{\partial W_{i j}^{'}} = \sum_{k = 1}^{V} \frac{\partial L}{\partial u_{k}} \frac{\partial u_{k}}{\partial W_{i j}^{'}} (2)

$\begin{equation} \frac{\partial\mathcal{L}}{\partial W'_{ij}} = \sum_{k=1}^V\frac{\partial\mathcal{L}}{\partial u_k}\frac{\partial u_k}{\partial W'_{ij}} \label{eq:dLdWp} \end{equation} \>(2)$

\frac{\partial L}{\partial W_{i j}} = \sum_{k = 1}^{V} \frac{\partial L}{\partial u_{k}} \frac{\partial u_{k}}{\partial W_{i j}} . (3)

$\begin{equation} \frac{\partial\mathcal{L}}{\partial W_{ij}} = \sum_{k=1}^V\frac{\partial\mathcal{L}}{\partial u_k}\frac{\partial u_k}{\partial W_{ij}}\ . \label{eq:dLdW} \end{equation} \>(3)$

, (2) (3) .

(2), Wij, W, i j , uj ( yj).

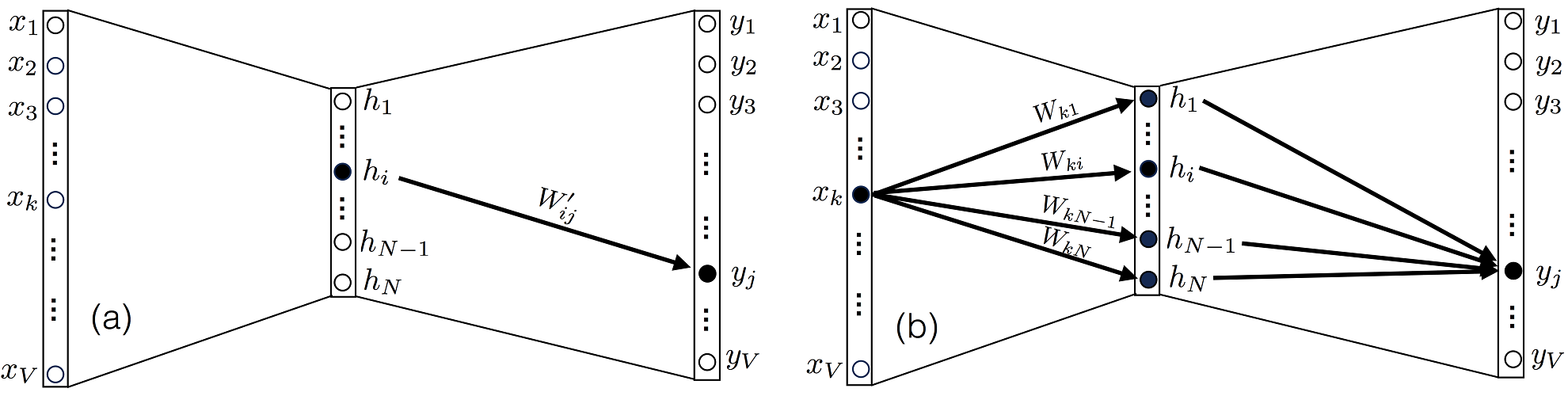
3. (a) $y_j$ $h_i$ $W'_{ij}$ $W'$ . (b) , $x_k$ N $W_{k1}\dots W_{kN}$ W.

, $\partial u_k/\partial W'_{ij}$ , , k=j, 0.

(4):

\frac{\partial L}{\partial W_{i j}^{'}} = \frac{\partial L}{\partial u_{j}} \frac{\partial u_{j}}{\partial W_{i j}^{'}} (4)

$\begin{equation} \frac{\partial\mathcal{L}}{\partial W'_{ij}} = \frac{\partial\mathcal{L}}{\partial u_j}\frac{\partial u_j} {\partial W'_{ij}} \label{eq:derivative#1} \end{equation} \>(4)$

$\partial \mathcal{L}/\partial u_j$ , (5):

\frac{\partial L}{\partial u_{j}} = - δ_{j j^{*}} + y_{j} := e_{j} (5)

$\begin{equation} \frac{\partial\mathcal{L}}{\partial u_j} = -\delta_{jj^*} + y_j := e_j \label{eq:term#1} \end{equation} \>(5)$

, $\delta_{jj^*}$ — , , 1, , 0 .

(5) e N ( ), , , .

(4) (6):

\frac{\partial u_{j}}{\partial W_{i j}^{'}} = \sum_{k = 1}^{V} W_{i k} x_{k} (6)

$\begin{equation} \frac{\partial u_j}{\partial W'_{ij}} = \sum_{k=1}^V W_{ik}x_k \label{eq:term#2} \end{equation} \>(6)$

(5) (6) (4) (7):

\frac{\partial L}{\partial W_{i j}^{'}} = (- δ_{j j^{*}} + y_{j}) (\sum_{k = 1}^{V} W_{k i} x_{k}) (7)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial\mathcal{L}}{\partial W'_{ij}} = (-\delta_{jj^*} + y_j) \left(\sum_{k=1}^V W_{ki}x_k\right) } \label{eq:backprop1} \end{equation} \>(7)$

$\partial\mathcal{L}/\partial W_{ij}$ , Xk, yj j W , 3(b). . $\partial u_k/\partial W_{ij}$ , uk u :

u_{k} = \sum_{m = 1}^{N} \sum_{l = 1}^{V} W_{m k}^{'} W_{l m} x_{l} .

$\begin{equation*} u_k = \sum_{m=1}^N\sum_{l=1}^VW'_{mk}W_{lm}x_l\ . \end{equation*}$

$\partial u_k/\partial W_{ij}$ , l=i m=j, (8):

\frac{\partial u_{k}}{\partial W_{i j}} = W_{j k}^{'} x_{i} . (8)

$\begin{equation} \frac{\partial u_k}{\partial W_{ij}} = W'_{jk}x_i\ . \label{eq:term#3} \end{equation} \>(8)$

(5) (8) , (9):

\frac{\partial L}{\partial W_{i j}} = \sum_{k = 1}^{V} (- δ_{k k^{*}} + y_{k}) W_{j k}^{'} x_{i} (9)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial \mathcal{L}}{\partial W_{ij}} = \sum_{k=1}^V (-\delta_{kk^*}+y_k)W'_{jk}x_i } \label{eq:backprop2} \end{equation} \>(9)$

. (7) (9) . (7)

\frac{\partial L}{\partial W^{'}} = (W^{T} x) \otimes e (10)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial\mathcal{L}}{\partial W'} = (W^T\textbf{x}) \otimes \textbf{e} } \end{equation} \>(10)$

⊗ .

(9) :

\frac{\partial L}{\partial W} = x \otimes (W^{'} e) (11)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial \mathcal{L}}{\partial W} = \textbf{x}\otimes(W'\textbf{e}) } \end{equation} \>(11)$

3.3

, (7) (9), , . . $\eta>0$ , :

\begin{array}{rcl} W_{new} & = W_{old} - η \frac{\partial L}{\partial W} \\ W_{new}^{'} & = W_{old}^{'} - η \frac{\partial L}{\partial W^{'}} \end{array}

$\begin{eqnarray} W_{\textrm{new}} & = W_{\textrm{old}} - \eta \frac{\partial \mathcal{L}}{\partial W} \nonumber \\ W'_{\textrm{new}} & = W'_{\textrm{old}} - \eta \frac{\partial \mathcal{L}}{\partial W'} \nonumber \\ \end{eqnarray}$

3.4

. , . , . , . , , , .

4. CBOW

CBOW . . (4) . OneHot Encoded . word2vec. .

4. CBOW

CBOW CBOW .

\begin{array}{rcl} h = & \frac{1}{C} W^{T} \sum_{c = 1}^{C} x^{(c)} = W^{T} \bar{x} \\ u = & W^{' T} h = \frac{1}{C} \sum_{c = 1}^{C} W^{' T} W^{T} x^{(c)} = W^{' T} W^{T} \bar{x} \\ y = & S oftmax (u) = S oftmax (W^{' T} W^{T} \bar{x}) \end{array}

$\begin{eqnarray} \textbf{h} = & \frac{1}{C} W^T \sum_{c=1}^C\textbf{x}^{(c)} = W^T\overline{\textbf{x}}\hspace{5.8cm} \nonumber \\ \textbf{u}= & W'^T\textbf{h}= \frac{1}{C}\sum_{c=1}^CW'^T W^T\textbf{x}^{(c)}=W'^T W^T\overline{\textbf{x}} \hspace{2.8cm} \nonumber \\ \textbf{y}= & \ \ \mathbb{S}\textrm{oftmax}(\textbf{u})= \mathbb{S}\textrm{oftmax}\left( W'^T W^T\overline{\textbf{x}}\right) \hspace{3.6cm} \nonumber \end{eqnarray}$

, '' $\overline{\textbf{x}}=\sum_{c=1}^C\textbf{x}^{(c)}/C$

, . :

L = - \log P (w_{o} | w_{c, 1}, w_{c, 2}, \dots, w_{c, C}) = - u_{j^{*}} + \log \sum_{i} \exp (u_{i}) . (12)

$\begin{equation} \mathcal{L} = -\log\mathbb{P}(w_o|w_{c,1},w_{c,2},\dots,w_{c,C})=-u_{j^*} + \log \sum_i \exp{(u_i)}. \end{equation} \>(12)$

, :

\frac{\partial L}{\partial W_{i j}^{'}} = \sum_{k = 1}^{V} \frac{\partial L}{\partial u_{k}} \frac{\partial u_{k}}{\partial W_{i j}^{'}} (13)

$\begin{equation} \frac{\partial\mathcal{L}}{\partial W'_{ij}} = \sum_{k=1}^V\frac{\partial\mathcal{L}}{\partial u_k}\frac{\partial u_k}{\partial W'_{ij}} \end{equation} \>(13)$

\frac{\partial L}{\partial W_{i j}} = \sum_{k = 1}^{V} \frac{\partial L}{\partial u_{k}} \frac{\partial u_{k}}{\partial W_{i j}} . (14)

$\begin{equation} \frac{\partial\mathcal{L}}{\partial W_{ij}} = \sum_{k=1}^V\frac{\partial\mathcal{L}}{\partial u_k}\frac{\partial u_k}{\partial W_{ij}}\ . \end{equation} \>(14)$

CBOW , , . $W’_{ij}$

$W_{ij}$ :

\frac{\partial L}{\partial W_{i j}} = \sum_{k = 1}^{V} \frac{\partial L}{\partial u_{k}} \frac{\partial}{\partial W_{i j}} (\frac{1}{C} \sum_{m = 1}^{N} \sum_{l = 1}^{V} W_{m k}^{'} \sum_{c = 1}^{C} W_{l m} x_{l}^{(c)}) = \frac{1}{C} \sum_{k = 1}^{V} \sum_{c = 1}^{C} (- δ_{k k^{*}} + y_{k}) W_{j k}^{'} x_{i}^{(c)} . (16)

$\begin{equation} \frac{\partial\mathcal{L}}{\partial W_{ij}} = \sum_{k=1}^V\frac{\partial\mathcal{L}}{\partial u_k}\frac{\partial}{\partial W_{ij}}\left(\frac{1}{C}\sum_{m=1}^N\sum_{l=1}^V W'_{mk}\sum_{c=1}^C W_{lm}x_l^{(c)}\right)=\frac{1}{C}\sum_{k=1}^V\sum_{c=1}^C(-\delta_{kk^*} + y_k)W'_{jk}x_i^{(c)} . \end{equation} \>(16)$

\frac{\partial L}{\partial W_{i j}^{'}} = (- δ_{j j^{*}} + y_{j}) (\sum_{k = 1}^{V} W_{k i} {\bar{x}}_{k}) (17)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial\mathcal{L}}{\partial W'_{ij}} = (-\delta_{jj^*} + y_j) \left(\sum_{k=1}^V W_{ki}\overline{x}_k\right) } \label{eq:backprop1_multi} \end{equation} \>(17)$

\frac{\partial L}{\partial W_{i j}} = \sum_{k = 1}^{V} (- δ_{k k^{*}} + y_{k}) W_{j k}^{'} {\bar{x}}_{i} . (18)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial\mathcal{L}}{\partial W_{ij}} = \sum_{k=1}^V(-\delta_{kk^*} + y_k)W'_{jk}\overline{x}_i . } \label{eq:backprop2_multi} \end{equation} \> (18)$

(17) (18) .
(17) :

\frac{\partial L}{\partial W^{'}} = (W^{T} \bar{x}) \otimes e (19)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial\mathcal{L}}{\partial W'} = (W^T\overline{\textbf{x}}) \otimes \textbf{e} } \end{equation} \>(19)$

(18):

\frac{\partial L}{\partial W} = \bar{x} \otimes (W^{'} e) (20)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial \mathcal{L}}{\partial W} =\overline{\textbf{x}}\otimes(W'\textbf{e}) } \end{equation} \>(20)$

, CBOW .
⊗ .

5. Skip-gram

CBOW, , . :

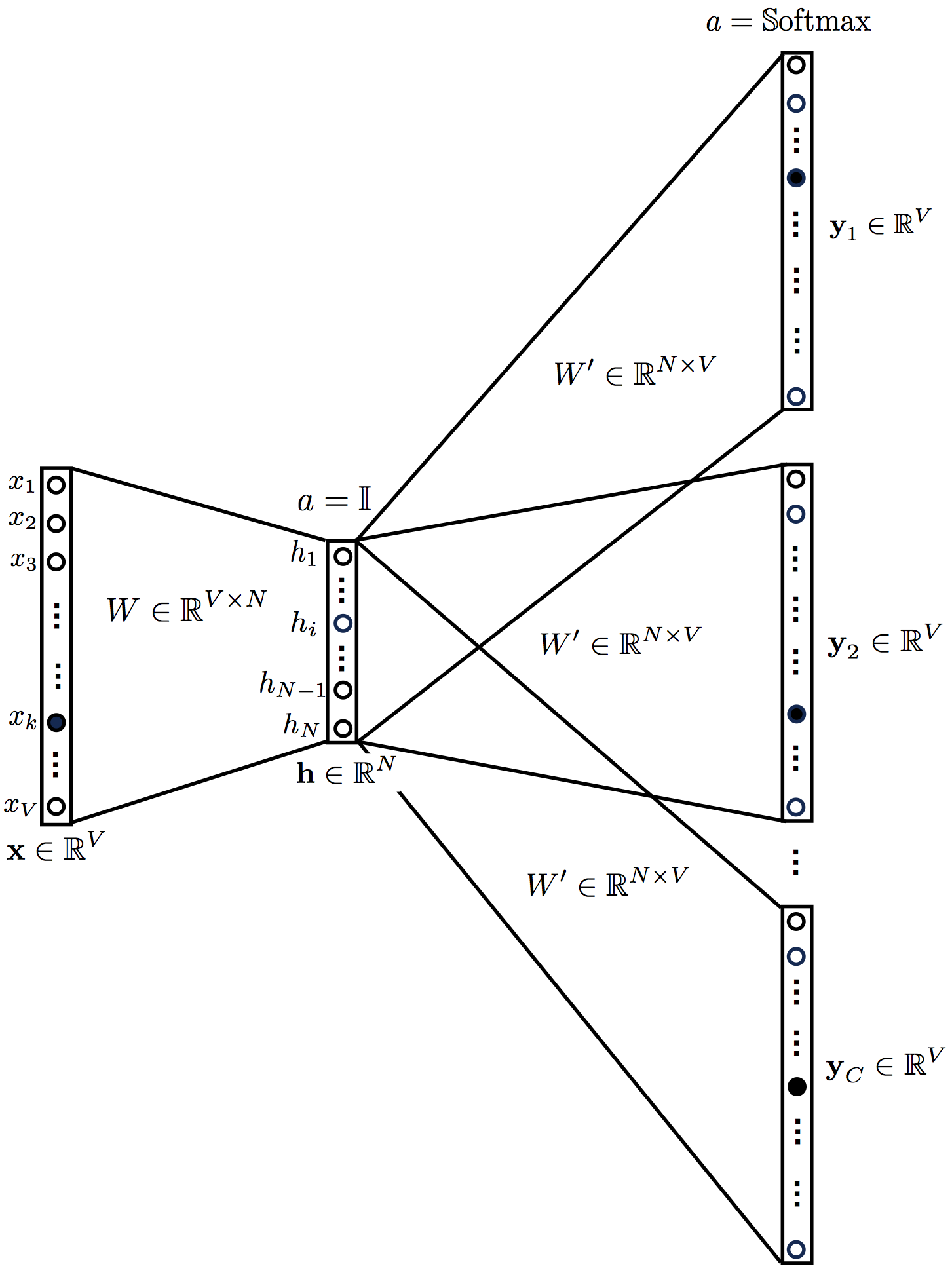
5. Skip-gram .

skip-gram :

\begin{array}{rcl} h = & W^{T} x \\ u_{c} = & W^{' T} h = W^{' T} W^{T} x c = 1, \dots, C \\ y_{c} = & S oftmax (u) = S oftmax (W^{' T} W^{T} x) c = 1, \dots, C \end{array}

$\begin{eqnarray*} \textbf{h} = & W^T\textbf{x} \hspace{9.4cm} \\ \textbf{u}_c= & W'^T\textbf{h}=W'^TW^T\textbf{x} \hspace{4cm} c=1, \dots, C \hspace{0.7cm}\\ \textbf{y}_c = & \ \ \mathbb{S}\textrm{oftmax}(\textbf{u})= \mathbb{S}\textrm{oftmax}(W'^TW^T\textbf{x}) \hspace{2cm} c=1, \dots, C \end{eqnarray*}$

( $\textbf{u}_c$ ) , $\mathbf{y}_1=\mathbf{y}_2\dots= \mathbf{y}_C$ . :

\begin{array}{rcl} L = - \log P (w_{c, 1}, w_{c, 2}, \dots, w_{c, C} | w_{o}) = - \log \prod_{c = 1}^{C} P (w_{c, i} | w_{o}) \\ = - \log \prod_{c = 1}^{C} \frac{\exp (u_{c, j^{*}})}{\sum_{j = 1}^{V} \exp (u_{c, j})} = - \sum_{c = 1}^{C} u_{c, j^{*}} + \sum_{c = 1}^{C} \log \sum_{j = 1}^{V} \exp (u_{c, j}) \end{array}

$\begin{eqnarray*} \mathcal{L} = -\log \mathbb{P}(w_{c,1}, w_{c,2}, \dots, w_{c,C}|w_o)=-\log \prod_{c=1}^C \mathbb{P}(w_{c,i}|w_o) \\ = -\log \prod_{c=1}^C \frac{\exp(u_{c,j^*})}{\sum_{j=1}^V \exp(u_{c,j})} =-\sum_{c=1}^C u_{c,j^*} + \sum_{c=1}^C \log \sum_{j=1}^V \exp(u_{c,j}) \end{eqnarray*}$

skip-gram $C\times V$
:

L = L (u_{1} (W, W^{'}), u_{2} (W, W^{'}), \dots, u_{C} (W, W^{'})) = L (u_{1, 1} (W, W^{'}), u_{1, 2} (W, W^{'}), \dots, u_{C, V} (W, W^{'}))

$\begin{equation*} \mathcal{L} = \mathcal{L}(\mathbf{u_1}(W,W'), \mathbf{u_2}(W,W'), \dots, \mathbf{u_C}(W,W'))\\=\mathcal{L}(u_{1,1}(W,W'), u_{1,2}(W,W'), \dots, u_{C,V}(W,W')) \end{equation*}$

\frac{\partial L}{\partial W_{i j}^{'}} = \sum_{k = 1}^{V} \sum_{c = 1}^{C} \frac{\partial L}{\partial u_{c, k}} \frac{\partial u_{c, k}}{\partial W_{i j}^{'}}

$\begin{equation*} \frac{\partial\mathcal{L}}{\partial W'_{ij}} = \sum_{k=1}^V\sum_{c=1}^C\frac{\partial\mathcal{L}}{\partial u_{c,k}}\frac{\partial u_{c,k}}{\partial W'_{ij}} \end{equation*}$

\frac{\partial L}{\partial W_{i j}} = \sum_{k = 1}^{V} \sum_{c = 1}^{C} \frac{\partial L}{\partial u_{c, k}} \frac{\partial u_{c, k}}{\partial W_{i j}} .

$\begin{equation*} \frac{\partial\mathcal{L}}{\partial W_{ij}} = \sum_{k=1}^V\sum_{c=1}^C\frac{\partial\mathcal{L}}{\partial u_{c,k}}\frac{\partial u_{c,k}}{\partial W_{ij}}\ . \end{equation*}$

$\partial \mathcal{L}/\partial u_{c,j}$ , :

\frac{\partial L}{\partial u_{c, j}} = - δ_{j j_{c}^{*}} + y_{c, j} := e_{c, j}

$\begin{equation*} \frac{\partial\mathcal{L}}{\partial u_{c,j}} = -\delta_{jj_c^*} + y_{c,j} := e_{c,j} \end{equation*}$

CBOW :

\frac{\partial L}{\partial W_{i j}^{'}} = \sum_{k = 1}^{V} \sum_{c = 1}^{C} \frac{\partial L}{\partial u_{c, k}} \frac{\partial u_{c, k}}{\partial W_{i j}^{'}} = \sum_{c = 1}^{C} \frac{\partial L}{\partial u_{c, j}} \frac{\partial u_{c, j}}{\partial W_{i j}^{'}} = \sum_{c = 1}^{C} (- δ_{j j_{c}^{*}} + y_{c, j}) (\sum_{k = 1}^{V} W_{k i} x_{k})

$\begin{equation*} \frac{\partial\mathcal{L}}{\partial W'_{ij}} = \sum_{k=1}^V\sum_{c=1}^C\frac{\partial\mathcal{L}}{\partial u_{c,k}}\frac{\partial u_{c,k}}{\partial W'_{ij}} = \sum_{c=1}^C\frac{\partial\mathcal{L}}{\partial u_{c,j}}\frac{\partial u_{c,j}}{\partial W'_{ij}} = \sum_{c=1}^C(-\delta_{jj_c^*} + y_{c,j}) \left(\sum_{k=1}^V W_{ki}x_k\right) \end{equation*}$

$W_{ij}$ , :

\frac{\partial L}{\partial W_{i j}} = \sum_{k = 1}^{V} \sum_{c = 1}^{C} \frac{\partial L}{\partial u_{c, k}} \frac{\partial}{\partial W_{i j}} (\sum_{m = 1}^{N} \sum_{l = 1}^{V} W_{m k}^{'} W_{l m} x_{l}) = \sum_{k = 1}^{V} \sum_{c = 1}^{C} (- δ_{k k_{c}^{*}} + y_{c, k}) W_{j k}^{'} x_{i} .

$\begin{equation*} \frac{\partial\mathcal{L}}{\partial W_{ij}} = \sum_{k=1}^V\sum_{c=1}^C\frac{\partial\mathcal{L}}{\partial u_{c,k}}\frac{\partial}{\partial W_{ij}}\left(\sum_{m=1}^N\sum_{l=1}^V W'_{mk} W_{lm}x_l\right)=\sum_{k=1}^V\sum_{c=1}^C (-\delta_{kk_c^*} + y_{c,k})W'_{jk}x_i . \end{equation*}$

, skip-gram :

\frac{\partial L}{\partial W_{i j}^{'}} = \sum_{c = 1}^{C} (- δ_{j j_{c}^{*}} + y_{c, j}) (\sum_{k = 1}^{V} W_{k i} x_{k}) (21)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial\mathcal{L}}{\partial W'_{ij}} = \sum_{c=1}^C(-\delta_{jj_c^*} + y_{c,j}) \left(\sum_{k=1}^V W_{ki}x_k\right) } \label{eq:backprop1_skip} \end{equation} \>(21)$

\frac{\partial L}{\partial W_{i j}} = \sum_{k = 1}^{V} \sum_{c = 1}^{C} (- δ_{k k_{c}^{*}} + y_{c, k}) W_{j k}^{'} x_{i} . (22)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial\mathcal{L}}{\partial W_{ij}} = \sum_{k=1}^V\sum_{c=1}^C (-\delta_{kk_c^*} + y_{c,k})W'_{jk}x_i . } \label{eq:backprop2_skip} \end{equation} \>(22)$

(21):

\frac{\partial L}{\partial W^{'}} = (W^{T} x) \otimes \sum_{c = 1}^{C} e_{c} (23)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial\mathcal{L}}{\partial W'} = (W^T\textbf{x}) \otimes \sum_{c=1}^C\textbf{e}_c } \end{equation} \>(23)$

(22):

\frac{\partial L}{\partial W} = x \otimes (W^{'} \sum_{c = 1}^{C} e_{c}) (24)

$\begin{equation} \bbox[white,5px,border:2px dotted red]{ \frac{\partial \mathcal{L}}{\partial W} = \textbf{x}\otimes\left(W'\sum_{c=1}^C\textbf{e}_c\right) } \end{equation} \>(24)$

6.

word2vec. . [2] ( softmax, negative sampling), . [1].

, word2vec.

. Python, .

[1] X. Rong, word2vec Parameter Learning Explained , arXiv: 1411.2738 (2014).
[2] T. Mikolov, K. Chen, G. Corrado, J. Dean, Estimativa eficiente de representações de palavras no espaço vetorial , arXiv: 1301.3781 (2013).

Algoritmo de propagação de erro de volta usando o Word2Vec como exemplo