Coderikuma vez observou: "Nunca há muitos filtros de Kalman" . O mesmo pode ser dito sobre o teorema de Bayes, porque, por um lado, é muito simples, mas, por outro, é tão difícil compreender sua profundidade.

O YouTube possui um maravilhoso canal Student Dave , mas o último vídeo foi postado seis anos atrás. O canal contém vídeos educativos nos quais o autor conta coisas complexas em uma linguagem muito simples: teorema de Bayes, filtro de Kalman, etc. O aluno Dave complementa sua história com um exemplo de cálculo no matlab.

Uma vez que sua vídeo aula chamada “Estimativa iterativa bayesiana” realmente me ajudou (no canal corresponde à lista de reprodução “Estimativa iterativa bayesiana: com MATLAB”) Queria que todos se familiarizassem com as explicações de Dave, mas infelizmente o projeto não é suportado. O próprio Dave não entra em contato. Você não pode adicionar uma tradução ao vídeo, pois o próprio autor deve iniciá-lo. Entrar em contato com o youtube não deu resultado, por isso decidi descrever o material em um artigo em russo e publicar onde ele é mais apreciado. O material é muito revisado e complementado, pois passou pela minha percepção subjetiva; portanto, colocá-lo como tradução seria inadequado. Mas peguei o sal da explicação de Dave. Reescrevi seu código em python, já que trabalho nele e o considero um bom substituto para pacotes matemáticos.

Portanto, se você quiser entender melhor o tópico do teorema de Bayes, seja bem-vindo.

Formulação do problema

, “ ”. .

-, . , . , . . , . . - .

, , , .

- $x$ . $x = 3$ . . .

( ) $N = 100$ () .

$\sigma_y^2=4$ .
, .

f_{p o s t e r i o r} (x) = \frac{f_{p r i o r} (x) \cdot f_{и з м} (x)}{\int f_{p r i o r} (x) \cdot f_{m e s} (x) d x},

$\begin{equation} f_{posterior}(x) = \frac{f_{prior}(x) \cdot f_{}(x)}{\int f_{prior}(x) \cdot f_{mes}(x) dx}, \end{equation}$

$f_{posterior}(x)$ — ;
$f_{prior}(x)$ — ;
$f_{mes}(x)$ — ( $L_x(sample)$ ).
. , ( , ):

f_{m e s} (x) = p d f (x = y, μ = x, σ = σ) = \frac{1}{2 π σ} e^{- \frac{(y - x)^{2}}{2 σ^{2}}},

$\begin{equation} f_{mes}(x) =pdf(x=y, \mu=x, \sigma=\sigma) = \frac{1}{2 \pi \sigma} e^{- \frac{(y-x)^2}{2\sigma^2}}, \end{equation}$

$pdf$ — ;
$\mu$ — ;
$\sigma$ — ;
$y$ — .
( $N$ ), , .

.
$\sigma$ , 99,7 %.

- , .

. -.
$(3, 5)$ . ( ) .

() , . .

:

f_{p o s t e r i o r} (X) = \frac{f_{p r i o r} (X) \cdot f_{и з м} (X)}{\int f_{p r i o r} (X) \cdot f_{m e s} (X) d X},

$\begin{equation} f_{posterior}(X) = \frac{f_{prior}(X) \cdot f_{}(X)}{\int f_{prior}(X) \cdot f_{mes}(X) dX}, \end{equation}$

$X$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ ;
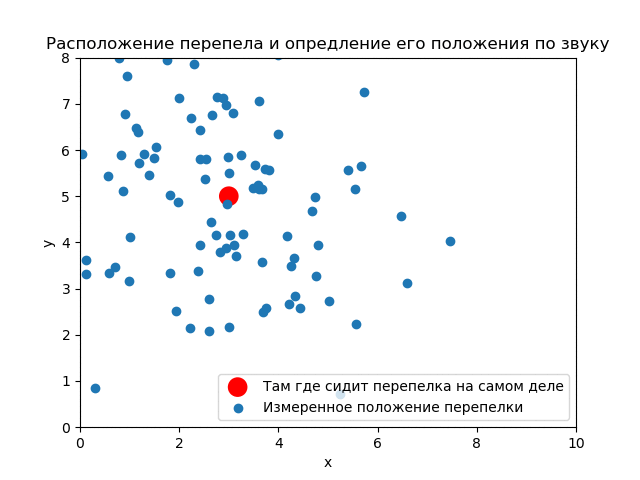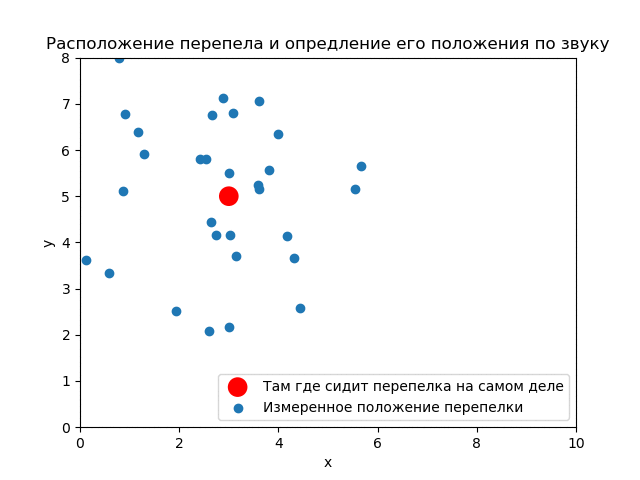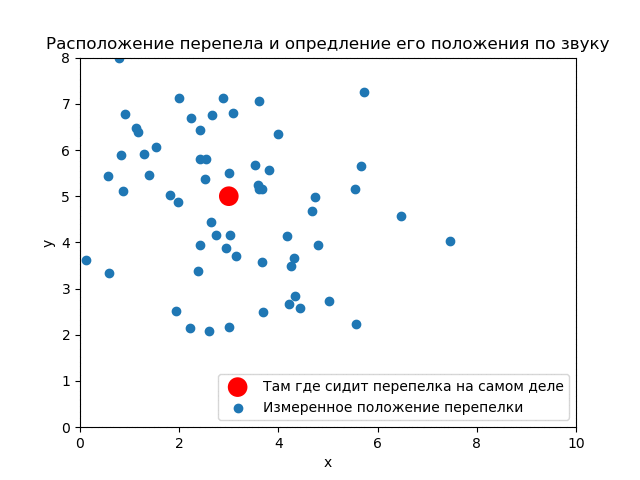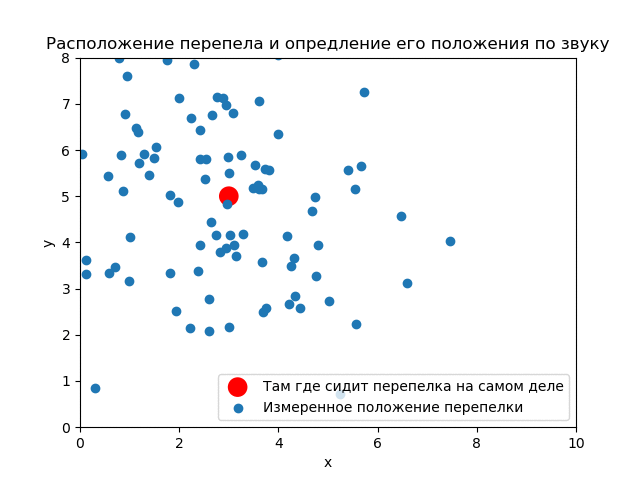
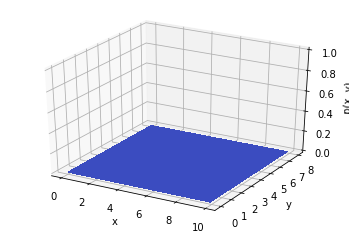
$f_{posterior}(X)$ — ;
$f_{prior}(X)$ — ;
$f_{mes}(X)$ — .
:

f_{m e s} (X) = \frac{1}{(2 π)^{2} d e t K} e^{\frac{1}{2} (Y - X)^{T} K^{- 1} (Y - X)},

$\begin{equation} f_{mes}(X) = \frac{1}{(2\pi)^2 detK} e^{ \frac {1}{2} (Y-X)^T K^{-1} (Y-X)}, \end{equation}$

$K$ — ;
$Y$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ .
, .

.

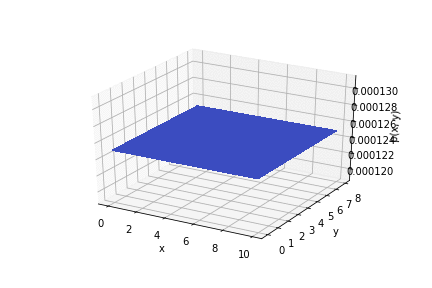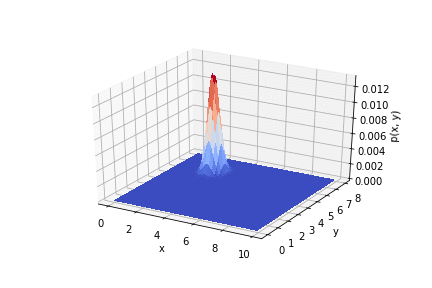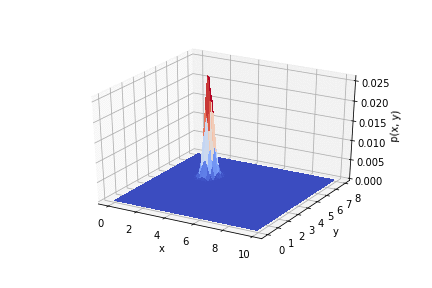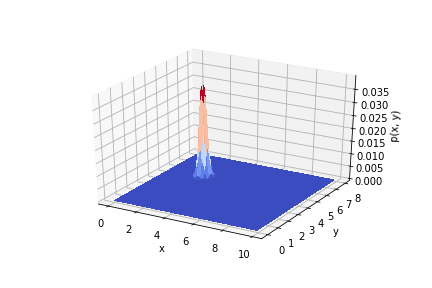
Assim, vê-se como os resultados do experimento afetam a distribuição a priori. Se você usar as medições corretamente, poderá obter uma boa precisão.
Mas não é mais fácil encontrar a média de todas as medições e, assim, fazer uma avaliação da localização da codorna? Claro. Este exemplo é apenas um bom exemplo do teorema de Bayes para variáveis aleatórias contínuas. O objetivo do artigo é resolver a teoria.

Pare no Dave Channel durante essas semanas de auto-isolamento. Bom para todos.

Ninja Bayesiano

Formulação do problema

More articles: