Olá! Quem tem que dia de quarentena? Força lateral coronavarius - ele matou todas as outras notícias. E todas as outras notícias, como você sabe, são ruins, então são boas notícias. Em geral, consultamos e decidimos nesta semana propor quebra-cabeças sobre o tema de ... vírus. Calmamente, você não pode se infectar com as decisões deles)Lave as mãos, fique em casa, não toque no rosto, aguarde respostas para os problemas exatamente uma semana depois.PS As respostas para os problemas da edição anterior já foram publicadas .
Em geral, consultamos e decidimos nesta semana propor quebra-cabeças sobre o tema de ... vírus. Calmamente, você não pode se infectar com as decisões deles)Lave as mãos, fique em casa, não toque no rosto, aguarde respostas para os problemas exatamente uma semana depois.PS As respostas para os problemas da edição anterior já foram publicadas .Questões
1. Doenças e testesDinoo está preocupado que ele possa ter uma doença rara. Ele decide fazer o teste e supõe que os métodos de teste para esta doença estejam corretos 99% das vezes (em outras palavras, se ele tiver a doença, isso mostra que ele faz isso com 99% de probabilidade e, se não tem a doença, mostra que ele não tem 99% de probabilidade). Suponha que essa doença seja realmente muito rara, ocorrendo aleatoriamente na população em geral em apenas uma em cada 10.000 pessoas.
Se os resultados de seus testes retornarem positivos, quais são suas chances de ele realmente ter a doença?
A. 0,99
B. 0,90
C. 0,10
D. 0,01
Transferir, . , 99 ( , , , 99- , , , 99- ). , , 10 000 .
, , ?
2. Problema estrito da programação das pílulasVocê está em um regime médico rigoroso que exige que você tome dois tipos de comprimidos por dia. Você deve tomar exatamente uma pílula A e exatamente uma pílula B ao mesmo tempo. Os comprimidos são muito caros e você não quer desperdiçar nenhum. Então você abre o frasco de pílulas A e bate uma na mão. Então você abre o frasco de pílulas B e faz a mesma coisa - mas comete um erro e duas pílulas B saem da sua mão com a pílula A. Mas as pílulas são exatamente idênticas. Não há como diferenciar as pílulas A além das pílulas B. É possível satisfazer o seu regime e tomar exatamente um de cada comprimido ao mesmo tempo, sem desperdiçar nenhum comprimido?
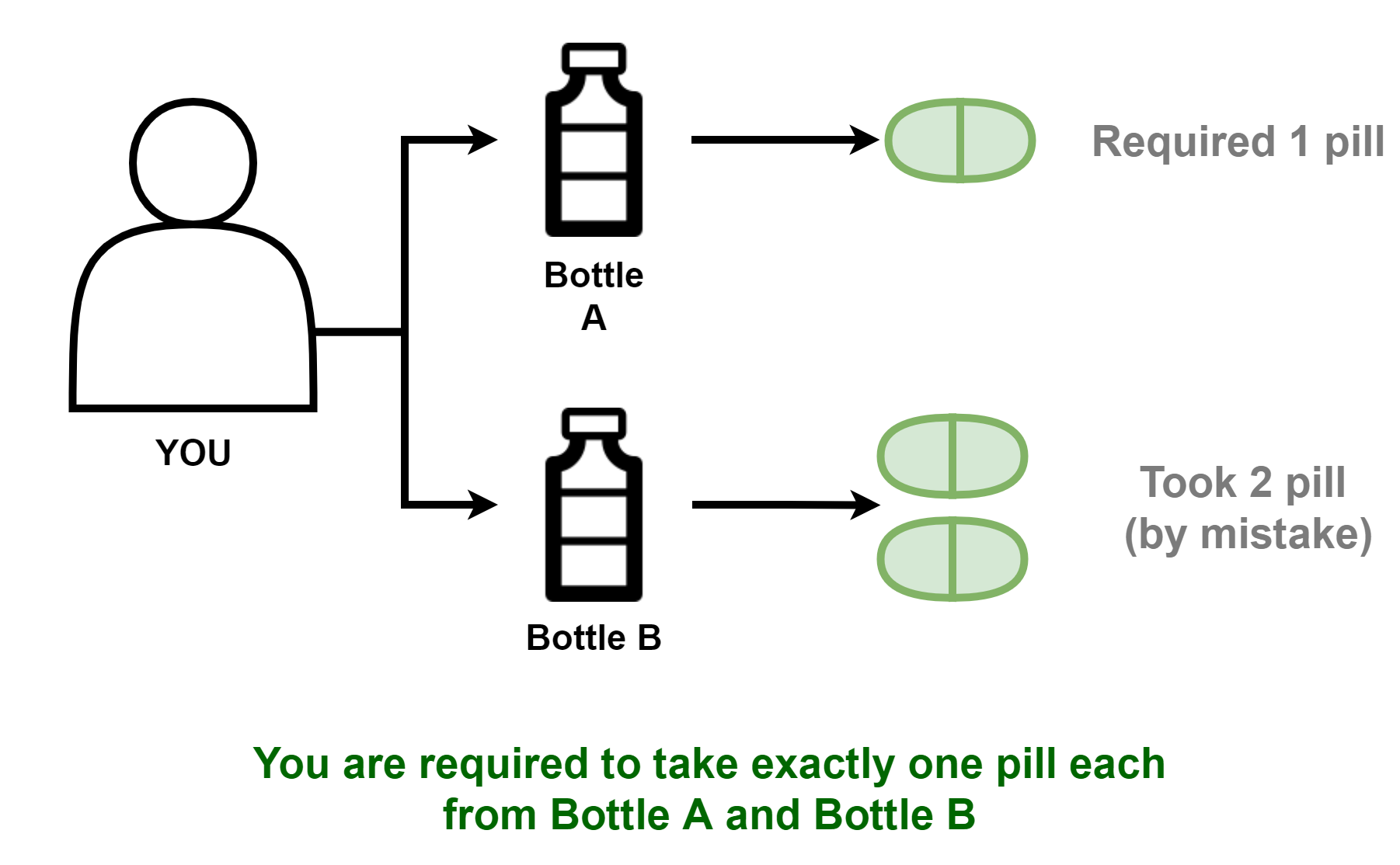
Transferir, . A B . , . , A . – , B . . A B. , ?
Tarefas
1. O problema do vírus em uma colônia bacterianaUm vírus entra em uma colônia composta por bactérias N. No primeiro minuto, destrói uma bactéria e depois se divide em dois novos vírus. Ao mesmo tempo, cada uma das bactérias restantes também é dividida em duas novas. No minuto seguinte, os dois vírus que desovam destroem duas bactérias e, em seguida, os vírus e todas as bactérias restantes se dividem novamente e assim por diante.
Sob essas condições, essa colônia viverá indefinidamente ou morrerá no final?
2. Organize o caminho!A new deadly virus has infected large population of a planet. A brilliant scientist has discovered a new strain of virus which can cure this disease. Vaccine produced from this virus has various strength depending on midichlorians count. A person is cured only if midichlorians count in vaccine batch is more than midichlorians count of person. A doctor receives a new set of report which contains midichlorians count of each infected patient, Practo stores all vaccine doctor has and their midichlorians count. You need to determine if doctor can save all patients with the vaccines he has. The number of vaccines and patients are equal.
Input Format:
First line No of test cases t followed by contains the number of vaccines — N. Second line contains N integers, which are strength of vaccines. Third line contains N integers, which are midichlorians count of patients.
Output Format:
Print a single line containing ′1′ for Yes or '0' for No.
Constraints:
1<=T<=150
1<=N<=10
Strength of vaccines and midichlorians count of patients fit in integer.
Sample Input:
2
5
123 146 454 542 456
100 328 248 689 200
8
87 93 50 22 63 28 91 60
64 27 41 27 73 37 12 69
Sample Output:
0
. , . , , . , , . , , Practo , , . , , . .
:
t, — N. N , . N , .
:
, «1» «0» .
:
1<=T<=150
1<=N<=10
.
:
2
5
123 146 454 542 456
100 328 248 689 200
8
87 93 50 22 63 28 91 60
64 27 41 27 73 37 12 69
:
0
1D — , , 1 .
:
() , . , ? , , ?
, A B, P (A|B) B A, P (B|A) A B:
P(A|B) = P(A)P(B|A) / P(B) => P(B) = P(A)P(B|A)/P(A/B)- — , , — , .
- , P(B|not A) — “ ”: , . P (B|A)=0.99, P (A)=0.0001, P (B) , A :
P(B)=P(B|A)P(A)+P(B|not A)P(not A) 0.99*0.0001+0.01*0.9999.
, , , 1 .
, , , , , . , , 1 . 100 , 99 . 999 900 , 9999 ( , - ). , , , , 99/(99+9999), , 0.0098 1 !
2:1: .
 2:
2: , , .
 3:
3: , .
 4:
4: . , ( ).

1: .
. , :

, t = N .
2#include<iostream>
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
int n,p=1;
cin>>n;
int a[n],b[n];
for(int i=0;i<n;i++)
cin>>a[i];
for(int i=0;i<n;i++)
cin>>b[i];
sort(a,a+n);
sort(b,b+n);
for(int i=0;i<n&&p;i++)
if(a[i]<b[i])
p=0;
cout<<p<<"\n";
}
return 0;
}