Dia bom.
No meu tempo livre, fiz uma pequena pesquisa.
Na teoria dos grafos, um algoritmo de número de cliques guloso é conhecido. Longe de sempre, ele dá o resultado certo. Sob o corte, há uma análise dos resultados do algoritmo ganancioso quando ele é combinado com a enumeração parcial dos conjuntos de vértices nos gráficos do conjunto de benchmarks DIMACS.
A coluna “Mais conhecido” da tabela 1 mostra os tamanhos dos cliques máximos atualmente conhecidos dos gráficos indicados. A coluna "Ganancioso" mostra os tamanhos máximos de cliques encontrados pelo algoritmo ganancioso. O algoritmo ganancioso fornece a resposta correta apenas em 3 casos em 35.
Nota - no código do programa implementado, o algoritmo ganancioso seleciona o vértice com o maior valor de adjacência. Se vários vértices semelhantes forem encontrados, o primeiro encontrado será selecionado. Vamos chamar o procedimento de algoritmo ganancioso Greedy (A), onde A é o número da matriz (matriz de adjacência) à qual o algoritmo é aplicado. Indexar a matriz inicial como A0.
Tabela 1 - Os resultados do algoritmo implementado em Pascal.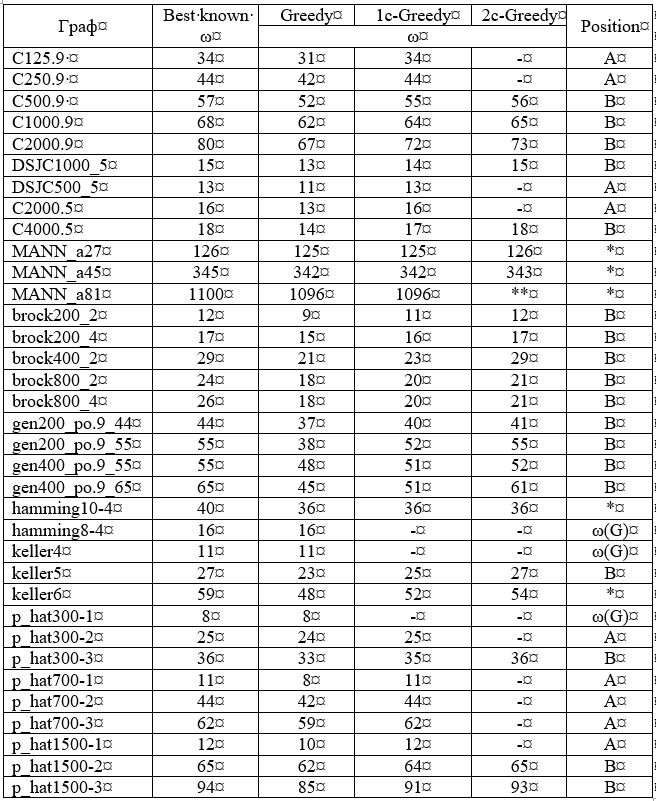 ** - não analisado devido ao grande tamanho do gráfico.
** - não analisado devido ao grande tamanho do gráfico., : N , . m, m – . DelNotAdj(m).
Greedy(m). ( ) «1c-Greedy». , , 8 35.
. , DelNotAdj(m). 0, m. mx. Greedy(mx). ( ) «2-Greedy».
3- (3c-Greedy) C500.9 C1000.9 ω(C500.9)=57, ω(C1000.9)=66.
.
Pascal Greedy(A) O(n2), n – . n , 2- – .. , ω(G) – () . .
, , ? 1 , .
( 1). O(n), – ω 1 ω(G) – , ωGR – , .
 1
1«Position» 1 . ꞷ(G) , . «» , .
«B» , 2- .
«*» , «», .. 2, 3 . ω. ωGRCFG.
, , , , . .. , , , 2- .
«» , :
- 0 «» . ωGR.
- «» m, m . m , . ωGR+1.
- «» mn, m- n- 0. mn , n- m- . ωGR+2.
- 3-, 4-,…, y- ωGR+3, ωGR+4,…, ωGR+y .
- 0 — ω(G).
. «» «B» :
, , ωGR. ωGR+1 ωGR, 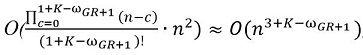 , K – .
, K – .
«*» :
«» ωGR, ωGR+1, ωGR+2,…, ω(G) . , , . , ωGR.
: ωGR, ωGR+1, ωGR+2,… , « » ( ωGRCDE 1).
:
1. «» ωGR+y,
ωGR+y-1, 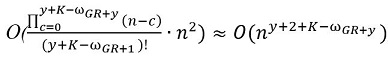 , K – .
, K – .
.
2. y- ωGR+y, , .. ωGR+y=ωGR+y-1, , ωGR+y ω(G) .
Se o acima exposto repetir o trabalho de outra pessoa, não estou despeito, ficarei feliz em ver o link. Ficarei ainda mais feliz se alguém teoricamente puder provar ou refutar as hipóteses propostas.