Os parâmetros e princípios de operação de vários sistemas podem ser conectados por um atributo selecionado entre si com vários tipos de relacionamentos. Se, digamos, estivermos interessados no efeito do preço de um serviço sobre sua demanda, essa relação pode ser descrita por uma relação do tipo "influências", "influências fortes", "influências fracas" etc. Nesse caso, objetos bastante “discretos” para descrição podem não ser suficientes. Para muitos problemas aplicados da teoria dos autômatos, reconhecimento de padrões, tomada de decisão, etc. faz sentido generalizar o conceito da relação entre objetos para um caso difuso. Nesse caso, o modelo, possivelmente, descreverá o sistema de maneira mais adequada, permitindo uma análise qualitativa de sistemas sem perda de informações limiares, em conexão com o surgimento de novos tipos de relacionamentos: similaridade, similaridade, dissimilaridade, ...
O conceito de relacionamentos difusos (conexões, associações, relacionamentos, relacionamentos são sinônimos), juntamente com o conceito de conjuntos difusos, refere-se aos fundamentos fundamentais de toda a teoria dos conjuntos difusos. Além do fato de eles próprios terem aplicado valor, com base em vários conceitos adicionais são determinados que são usados para criar modelos difusos de sistemas mais complexos.
Relação difusa
 (desculpa)
(desculpa)Definição
Como no caso dos conjuntos nebulosos (HMs), os relacionamentos nebulosos generalizam o conceito do relacionamento usual com o qual estamos familiarizados na teoria dos conjuntos (ingênua). E muitos conceitos introduzidos abaixo para as relações serão semelhantes aos conceitos correspondentes para NM.
Introduzimos os conceitos de relacionamento difuso e consideramos suas propriedades.
Proporção difusa de 2 árias (binária) no conjunto universal , . :
n- n- .
, - ( , ..). . . , n- .
.
- ;
- ;
- ;
- , — , — . ( , . , , , xD)
.
Deixe no set razão difusa definida "muito maior" (x >> y). Então a matriz dessa relação e o gráfico terão a forma, respectivamente:

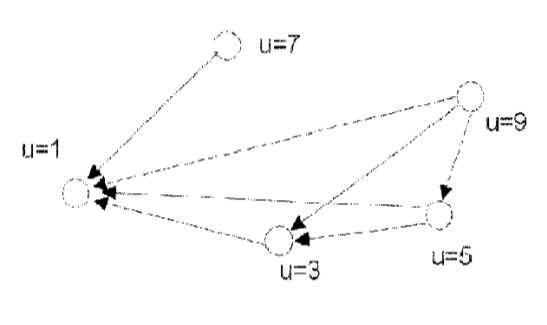
—
:
,
( ) :
:
:
, , — .
, :
, , 0.5 0.
, .
:
. O conjunto de todas as relações difusas forma uma rede distributiva em relação às operações de união e interseção; e do cumprimento das identidades de idempotência, comutatividade, associatividade, absorção e distributividade para a rede segue-se o cumprimento dessas identidades para todas as relações.Na lógica baseada na teoria dos conjuntos comuns, uma afirmação como "os números xey são muito próximos ou muito diferentes" deve ser reduzida para "os números xey são muito próximos ou muito diferentes". No entanto, na teoria dos conjuntos nebulosos, a primeira afirmação é bastante lógica; expressa o fato de que o conectivo “e” é interpretado por valores muito pequenos da função de associação, quando é impossível dizer sobre xey que eles são muito próximos ou que são muito diferentes um do outro. Este exemplo ilustra bem a flexibilidade de enunciados inerentes à lógica real.
: ; : .
, . - . , . - . , .
( ) . .
. , . (Max-*)-. , 3 .
- max-min ( ): . .
- min-max ( ): .
- max-• ( ): .
Que haja duas relações em, . :
:
- ;
- ;
- .
. :
:;
: ;
: ;
flexx: ;
: ;
: ;
: ;
: .
… . .
2 NPC-, . , . NPC :
, , .
, , — .
, , :
« »
« »
« »
. : NPC ?
, :
def very(arr: List[set]):
return [(elem[0]**2, elem[1]) for elem in arr]
def no(arr: List[set]):
return [(1 - elem[0], elem[1]) for elem in arr]
def attitude(a: List[set], b: List[set], func = lambda x, y: min(x, y)):
return [[func(i[0], j[0]) for j in b] for i in a]
def attitude_unite(a: List[List], b: List[List]):
return [[max(a[i][j], b[i][j]) for j in range(len(a[i]))] for i in range(len(a))]
def composition(a: List[List], b: List[List]):
result = [[0 for j in range(len(b[0]))] for i in range(len(a))]
for x in range(len(a)):
for z in range(len(b[0])):
maximum = min(a[x][0], b[0][z])
for y in range(0, len(a[0])):
if maximum < min(a[x][y], b[y][z]):
maximum = min(a[x][y], b[y][z])
result[x][z] = maximum
return result
def index_plus(a: List[List]):
maximum = max([elem[1] for elem in a])
result = 0
for i in range(len(a)):
result += a[i][0] * (a[i][1] + maximum) / 2
return result
def ranking_index(a: List[List], b: List[List]):
return index_plus(a) - index_plus(b)
, — -. , , , index_plus ranking_index. . ( ; , ) :
— . . :
A = [(0.8, 3), (0.4, 15), (0.3, 30)]
B = [(0.1, 0.9), (0.5, 0.5), (0.8, 0.1)]
C = [(0.8, 0.9), (0.5, 0.5), (0.3, 0.2)]
— « ». 1 3 :
x = no(very(A))
x = [[elem[0] for elem in x]]
NPC K1R1. R1=A×B ∪ A¯×B¯:
AonB = attitude(A, B)
notAonnotB = attitude(no(A), no(B))
R1 = attitude_unite(AonB, notAonnotB)
y1, ( ) R1.
y1 = composition(x, R1)
print('y1 = ', y1)
:
notAonC = attitude(no(A), C)
AonnotC = attitude(A, no(C))
R2 = attitude_unite(notAonC, AonnotC)
y2 = composition(x, R2)
print('y2 = ', y2)
y1y2:
y1 = [(y1[0][i], B[i][1]) for i in range(len(y1[0]))]
y2 = [(y2[0][i], C[i][1]) for i in range(len(y2[0]))]
NPC:
print('index = ', ranking_index(y1, y2))
Um pequeno valor negativo indica que K2aceitar itens com mais lealdade e é mais provável contar a busca pelo jogador do que K1.
E isso é tudo por hoje.