Olá Habr!Lembramos que, anteriormente, anunciamos o livro " Machine Learning Without Extra Words " - e agora já está à venda . Apesar do fato de que, para iniciantes no MO, o livro pode realmente se tornar uma área de trabalho , alguns tópicos ainda não foram abordados. Portanto, estamos oferecendo a todos os interessados a tradução de um artigo de Simon Kerstens sobre a essência dos algoritmos do MCMC com a implementação de um algoritmo desse tipo em Python.Os métodos de Monte Carlo para cadeias de Markov (MCMC) são uma poderosa classe de métodos para amostragem de distribuições de probabilidade conhecidas apenas até uma constante de normalização (desconhecida).No entanto, antes de investigar o MCMC, vamos discutir por que você pode precisar fazer essa seleção. A resposta é: você pode estar interessado nas próprias amostras da amostra (por exemplo, para determinar parâmetros desconhecidos usando o método de derivação bayesiana) ou para aproximar os valores esperados das funções em relação à distribuição de probabilidade (por exemplo, para calcular quantidades termodinâmicas da distribuição de estados na física estatística). Às vezes, estamos interessados apenas no modo de distribuição de probabilidade. Nesse caso, é obtido pelo método de otimização numérica, portanto não é necessário fazer uma seleção completa.Acontece que a amostragem de quaisquer distribuições de probabilidade, exceto as mais primitivas, é uma tarefa difícil. O método de transformação inversa é uma técnica elementar para amostragem de distribuições de probabilidade, que, no entanto, requer o uso de uma função de distribuição cumulativa e, para usá-la, por sua vez, é necessário conhecer a constante de normalização, que geralmente é desconhecida. Em princípio, uma constante de normalização pode ser obtida por integração numérica, mas esse método rapidamente se torna impraticável com um aumento no número de dimensões. Amostragem de desvioNão requer uma distribuição normalizada, mas para implementá-la efetivamente, é preciso muito conhecimento sobre a distribuição de interesse para nós. Além disso, esse método sofre severamente com a maldição das dimensões - isso significa que sua eficácia diminui rapidamente com um aumento no número de variáveis. É por isso que você precisa organizar de maneira inteligente o recebimento de amostras representativas da sua distribuição - sem precisar conhecer a constante de normalização.Os algoritmos MCMC são uma classe de métodos projetados especificamente para isso. Eles voltam ao artigo de referência de Metropolis e outros ; Metropolis desenvolveu o primeiro algoritmo MCMC em homenagem a elee projetado para calcular o estado de equilíbrio de um sistema bidimensional de esferas duras. De fato, os pesquisadores procuravam um método universal que nos permitisse calcular os valores esperados encontrados na física estatística.Este artigo abordará os conceitos básicos de amostragem MCMC.CORRENTES DE MARKOVAgora que entendemos por que precisamos provar, vamos para o coração das cadeias MCMC: Markov. O que é uma cadeia de Markov? Sem entrar em detalhes técnicos, podemos dizer que uma cadeia de Markov é uma sequência aleatória de estados em um determinado espaço de estados, onde a probabilidade de escolher um determinado estado depende apenas do estado atual da cadeia, mas não de sua história anterior: essa cadeia é desprovida de memória. Sob certas condições, uma cadeia de Markov possui uma distribuição estacionária única de estados, para a qual converge, superando um certo número de estados. Após esse número de estados em uma cadeia de Markov, é obtida uma distribuição invariável.Para amostrar de uma distribuição, 
o algoritmo MCMC cria e simula uma cadeia de Markov cuja distribuição estacionária é; isto significa que, após o período inicial de "semente", os estados dessa cadeia de Markov são distribuídos de acordo com o princípio . Portanto, teremos que salvar apenas o estado para obter amostras .Para fins educacionais, consideremos um espaço de estado discreto e um "tempo" discreto. A quantidade principal que caracteriza uma cadeia de Markov é um operador de transição, 
indicando a probabilidade de estar em um estado de 
cada vez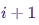 
, desde que a cadeia esteja em um estado de 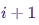cada vez i.Agora, apenas por diversão (e como demonstração), vamos tecer rapidamente uma cadeia de Markov com uma distribuição estacionária exclusiva. Vamos começar com algumas importações e configurações para gráficos:%matplotlib notebook
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 6]
np.random.seed(42)
A cadeia de Markov contornará o espaço de estado discreto formado por três condições climáticas:state_space = ("sunny", "cloudy", "rainy")
Em um espaço de estado discreto, o operador de transição é apenas uma matriz. No nosso caso, as colunas e linhas correspondem ao tempo ensolarado, nublado e chuvoso. Vamos escolher valores relativamente razoáveis para as probabilidades de todas as transições:transition_matrix = np.array(((0.6, 0.3, 0.1),
(0.3, 0.4, 0.3),
(0.2, 0.3, 0.5)))
As linhas indicam os estados nos quais o circuito pode estar localizado no momento e as colunas indicam os estados nos quais o circuito pode ir. Se dermos o passo "tempo" da cadeia de Markov em uma hora, desde que esteja ensolarado agora, há 60% de chance de que o tempo ensolarado continue pela próxima hora. Há também uma chance de 30% de tempo nublado na próxima hora e 10% de chuva imediatamente após o tempo ensolarado. Isso também significa que os valores em cada linha somam um.Vamos dirigir um pouco a nossa cadeia de Markov:n_steps = 20000
states = [0]
for i in range(n_steps):
states.append(np.random.choice((0, 1, 2), p=transition_matrix[states[-1]]))
states = np.array(states)
Podemos observar como a cadeia de Markov converge para uma distribuição estacionária, calculando a probabilidade empírica de cada um dos estados em função do comprimento da cadeia:def despine(ax, spines=('top', 'left', 'right')):
for spine in spines:
ax.spines[spine].set_visible(False)
fig, ax = plt.subplots()
width = 1000
offsets = range(1, n_steps, 5)
for i, label in enumerate(state_space):
ax.plot(offsets, [np.sum(states[:offset] == i) / offset
for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
despine(ax, ('top', 'right'))
plt.show()
HONRA DE TODO MCMC: ALGORITMO DE METROPOLIS-HASTINGSObviamente, tudo isso é muito interessante, mas voltando ao processo de amostragem de uma distribuição de probabilidade arbitrária 
. Pode ser discreto, caso em que continuaremos a falar sobre a matriz de transição 
ou contínuo, caso em que será um núcleo de transição. A seguir, falaremos sobre distribuições contínuas, mas todos os conceitos que consideramos aqui também são aplicáveis a casos discretos.Se pudéssemos projetar o núcleo de transição de tal maneira que o próximo estado já fosse deduzido , isso poderia ser limitado, já que nossa cadeia de Markov ... seria diretamente amostrada . Infelizmente, para conseguir isso, precisamos da capacidade de amostraro que não podemos fazer - caso contrário, você não leria isso, certo?A solução alternativa é dividir o núcleo da transição 
em duas partes: a etapa da proposta e a etapa de aceitação / rejeição. Uma distribuição auxiliar aparece na etapa de amostra
a partir da qual os possíveis próximos estados da cadeia são selecionados. Não apenas podemos fazer uma seleção dessa distribuição, mas podemos escolher arbitrariamente a própria distribuição. No entanto, ao projetar, deve-se buscar uma configuração na qual as amostras colhidas nessa distribuição sejam minimamente correlacionadas com o estado atual e, ao mesmo tempo, tenham boas chances de passar pela fase de recebimento. A etapa de recebimento / descarte acima é a segunda parte do núcleo de transição; nesse estágio, os erros contidos nos estados de teste selecionados são corrigidos 
. Aqui, a probabilidade de recepção bem-sucedida é calculada 
e uma amostra é coletada com a mesma probabilidade que o próximo estado da cadeia. Obtendo o próximo estado dedepois, é executado da seguinte forma: primeiro, o estado do teste é retirado . Em seguida, é tomado como o próximo estado com probabilidade ou descartado com probabilidade 
e, no último caso, o estado atual é copiado e usado como o próximo.Por conseguinte, temos
condição suficiente para a cadeia de Markov teve como uma distribuição estacionária é a seguinte: O núcleo de transição deve apresentar equilíbrio detalhado ou como escrita na literatura física, reversibilidade microscópica :
.Isso significa que a probabilidade de estar em um estado 
e passar de lá para
deve ser igual à probabilidade do processo inverso, ou seja, poder entrar e entrar em um estado . Os núcleos de transição da maioria dos algoritmos MCMC atendem a essa condição.Para que o núcleo de transição em duas partes obedeça ao equilíbrio detalhado, é necessário escolher corretamente 
, ou seja, garantir que ele permita corrigir quaisquer assimetrias no fluxo de probabilidade de / para ou . O algoritmo de Metropolis-Hastings usa o critério de admissibilidade
.E aqui começa a mágica: sabemos apenas uma constante, mas isso não importa, pois essa constante desconhecida anula a expressão de! É essa propriedade paccpacc que garante a operação de algoritmos baseados no algoritmo Metropolis-Hastings em distribuições não normalizadas. As distribuições auxiliares simétricas c são frequentemente usadas 
; nesse caso, o algoritmo Metropolis-Hastings é reduzido ao algoritmo original (menos geral) Metropolis desenvolvido em 1953. No algoritmo original
.Nesse caso, o núcleo transitório completo do Metropolis-Hastings pode ser escrito como
.IMPLEMENTAM O ALGORITMO DE METROPOLIS-HASTINGS NA PYTHONBem, agora que descobrimos como o algoritmo Metropolis-Hastings funciona, vamos prosseguir para sua implementação. Primeiro, estabelecemos a probabilidade logarítmica da distribuição a partir da qual vamos fazer uma seleção - sem constantes de normalização; supõe-se que não os conhecemos. Em seguida, trabalhamos com a distribuição normal padrão:def log_prob(x):
return -0.5 * np.sum(x ** 2)
Em seguida, escolhemos uma distribuição auxiliar simétrica. Em geral, o desempenho do algoritmo Metropolis-Hastings pode ser aprimorado se você incluir informações já conhecidas sobre a distribuição a partir da qual deseja fazer uma seleção na distribuição auxiliar. Uma abordagem simplificada se parece com isso: pegamos o estado atual xe selecionamos uma amostra , ou seja, definimos um determinado tamanho de etapa Δe seguimos para a esquerda ou direita do nosso estado atual em não mais do que 
:def proposal(x, stepsize):
return np.random.uniform(low=x - 0.5 * stepsize,
high=x + 0.5 * stepsize,
size=x.shape)
Por fim, calculamos a probabilidade de a proposta ser aceita:def p_acc_MH(x_new, x_old, log_prob):
return min(1, np.exp(log_prob(x_new) - log_prob(x_old)))
Agora reunimos tudo isso em uma implementação verdadeiramente breve do estágio de amostragem do algoritmo Metropolis-Hastings:def sample_MH(x_old, log_prob, stepsize):
x_new = proposal(x_old, stepsize)
accept = np.random.random() < p_acc(x_new, x_old, log_prob)
if accept:
return accept, x_new
else:
return accept, x_old
Além do próximo estado na cadeia Markov, x_newou x_old, também retornamos informações sobre se a etapa do MCMC foi adotada. Isso nos permitirá acompanhar a dinâmica da coleta de amostras. Na conclusão desta implementação, escrevemos uma função que chamará iterativamente sample_MHe, assim, criará uma cadeia de Markov:def build_MH_chain(init, stepsize, n_total, log_prob):
n_accepted = 0
chain = [init]
for _ in range(n_total):
accept, state = sample_MH(chain[-1], log_prob, stepsize)
chain.append(state)
n_accepted += accept
acceptance_rate = n_accepted / float(n_total)
return chain, acceptance_rate
TESTANDO O NOSSO ALGORITMO DE METROPÓLIS E INVESTIGANDO SEU COMPORTAMENTOProvavelmente, agora você mal pode esperar para ver tudo isso em ação. Faremos isso, tomaremos algumas decisões informadas sobre os argumentos stepsizee n_total:chain, acceptance_rate = build_MH_chain(np.array([2.0]), 3.0, 10000, log_prob)
chain = [state for state, in chain]
print("Acceptance rate: {:.3f}".format(acceptance_rate))
last_states = ", ".join("{:.5f}".format(state)
for state in chain[-10:])
print("Last ten states of chain: " + last_states)
Acceptance rate: 0.722
Last ten states of chain: -0.84962, -0.84962, -0.84962, -0.08692, 0.92728, -0.46215, 0.08655, -0.33841, -0.33841, -0.33841
As coisas estão boas. Então, funcionou? Conseguimos colher amostras em cerca de 71% dos casos e temos uma cadeia de estados. Os primeiros estados em que a cadeia ainda não convergiu para sua distribuição estacionária devem ser descartados. Vamos verificar se as condições que escolhemos realmente têm uma distribuição normal:def plot_samples(chain, log_prob, ax, orientation='vertical', normalize=True,
xlims=(-5, 5), legend=True):
from scipy.integrate import quad
ax.hist(chain, bins=50, density=True, label="MCMC samples",
orientation=orientation)
if normalize:
Z, _ = quad(lambda x: np.exp(log_prob(x)), -np.inf, np.inf)
else:
Z = 1.0
xses = np.linspace(xlims[0], xlims[1], 1000)
yses = [np.exp(log_prob(x)) / Z for x in xses]
if orientation == 'horizontal':
(yses, xses) = (xses, yses)
ax.plot(xses, yses, label="true distribution")
if legend:
ax.legend(frameon=False)
fig, ax = plt.subplots()
plot_samples(chain[500:], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
Parece ótimo!E os parâmetros stepsizee n_total? Primeiro discutimos o tamanho da etapa: ela determina até que ponto o estado de teste pode ser removido do estado atual do circuito. Portanto, este é um parâmetro de distribuição auxiliar qque controla o tamanho das etapas aleatórias tomadas pela cadeia de Markov. Se o tamanho da etapa for muito grande, os estados do teste geralmente acabam na cauda da distribuição, onde os valores de probabilidade são baixos. O mecanismo de amostragem Metropolis-Hastings descarta a maioria dessas etapas, como resultado das taxas de recepção reduzidas e a convergência diminui significativamente. Veja por si mesmo:def sample_and_display(init_state, stepsize, n_total, n_burnin, log_prob):
chain, acceptance_rate = build_MH_chain(init_state, stepsize, n_total, log_prob)
print("Acceptance rate: {:.3f}".format(acceptance_rate))
fig, ax = plt.subplots()
plot_samples([state for state, in chain[n_burnin:]], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
sample_and_display(np.array([2.0]), 30, 10000, 500, log_prob)
Acceptance rate: 0.116
Não é muito legal, né? Agora parece que é melhor definir um pequeno tamanho de passo. Acontece que essa também não é uma decisão inteligente, já que a cadeia de Markov investigará a distribuição de probabilidade muito lentamente e, portanto, também não convergirá tão rapidamente quanto com um tamanho de etapa bem escolhido:sample_and_display(np.array([2.0]), 0.1, 10000, 500, log_prob)
Acceptance rate: 0.992
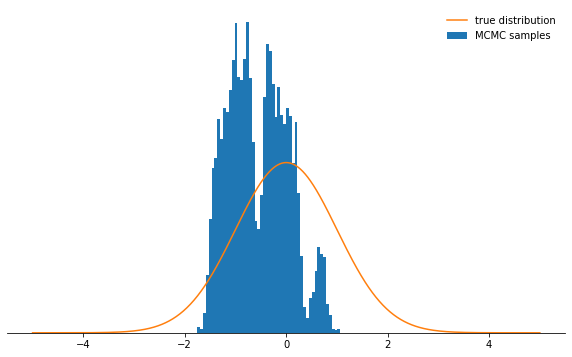Independentemente de como você escolhe o parâmetro de tamanho da etapa, a cadeia de Markov eventualmente converge para uma distribuição estacionária. Mas isso pode levar muito tempo. O tempo durante o qual simularemos a cadeia de Markov é n_totaldeterminado pelo parâmetro - ele simplesmente determina quantos estados da cadeia de Markov (e, portanto, as amostras selecionadas) teremos eventualmente. Se a cadeia convergir lentamente, ela precisará ser aumentada n_totalpara que a cadeia de Markov tenha tempo para "esquecer" o estado inicial. Portanto, deixaremos o tamanho da etapa pequeno e aumentaremos o número de amostras aumentando o parâmetro n_total:sample_and_display(np.array([2.0]), 0.1, 500000, 25000, log_prob)
Acceptance rate: 0.990
Certamente, estamos avançando em direção ao objetivo ...CONCLUSÕESConsiderando tudo o que foi dito acima, espero que agora você tenha compreendido intuitivamente a essência do algoritmo Metropolis-Hastings, seus parâmetros e entenda por que essa é uma ferramenta extremamente útil para selecionar distribuições de probabilidades não padrão que você possa encontrar na prática.Eu recomendo fortemente que você experimente o código fornecido aqui.- para que você se acostume com o comportamento do algoritmo em várias circunstâncias e o entenda mais profundamente. Experimente a distribuição auxiliar assimétrica! O que acontecerá se você não configurar o critério de aceitação corretamente? O que acontece se você tentar amostrar a partir de uma distribuição bimodal? Você pode encontrar uma maneira de ajustar automaticamente o tamanho da etapa? Quais são as armadilhas aqui? Responda a estas perguntas você mesmo!