Este artigo propõe um método de indução difusa desenvolvido pelo autor como uma combinação das disposições da matemática difusa e da teoria fractal, introduz o conceito do grau de recursão de um conjunto difuso, descreve a recursão incompleta de um conjunto como sua dimensão fracionária para modelar um domínio de sujeito. Como o escopo do método proposto e os modelos de conhecimento criados com base em conjuntos difusos, é considerado o gerenciamento do ciclo de vida dos sistemas de informação, incluindo o desenvolvimento de cenários para o uso e teste de software.
Relevância
No processo de projetar e desenvolver, implementar e operar sistemas de informação, é necessário acumular e sistematizar dados, informações e informações coletadas externamente ou que surjam em cada estágio do ciclo de vida do software. Isso serve como o suporte informativo e metodológico necessário para o trabalho de design e a tomada de decisões, e é especialmente relevante em situações de alta incerteza e em ambientes mal estruturados. A base de conhecimento formada como resultado do acúmulo e sistematização de tais recursos não deve ser apenas uma fonte de experiência útil adquirida pela equipe do projeto durante o trabalho de criação de um sistema de informação, mas também a maneira mais simples de modelar novas visões, métodos e algoritmos para implementar tarefas do projeto. Em outras palavras,essa base de conhecimento é um repositório de capital intelectual e, ao mesmo tempo, uma ferramenta de gerenciamento de conhecimento [3, 10].
Eficiência, utilidade, qualidade da base de conhecimento como ferramenta se correlacionam com a intensidade de recursos de sua manutenção e a eficácia da extração de conhecimento. Quanto mais simples e mais rápida a coleta e a fixação do conhecimento no banco de dados e mais pertinentes forem os resultados das consultas, melhor e mais confiável será a própria ferramenta [1, 2]. No entanto, métodos discretos e ferramentas de estruturação aplicáveis aos sistemas de gerenciamento de banco de dados, incluindo a normalização de relacionamentos relacionais, não permitem descrever ou modelar componentes semânticos, interpretações, intervalos e conjuntos semânticos contínuos [4, 7, 10]. Para isso, precisamos de uma abordagem metodológica que generalize casos particulares de ontologias finitas e aproxime o modelo de conhecimento da continuidade da descrição da área de assunto do sistema de informação.
[3, 6]. ( ) ( – , , ), ( ), , – , , [5, 8, 9].
X – :
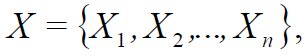 (1)
(1)
n = [N ≥ 3] – (, (0; 1) – (; )).
X = B, B = {a,b,c,...,z} – , X.
 , ( ) , X, :
, ( ) , X, :
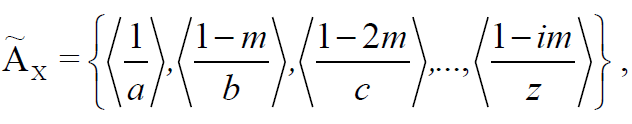 (2)
(2)
m – , i N – .
, () , ,  :
:
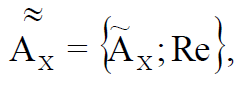 (3)
(3)
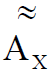 – , , X,
– , , X,  , ; Re – .
, ; Re – .
, 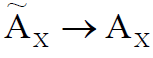 ( ) .
( ) .
Re = 1 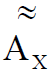 2- , ( ), X [1, 2]:
2- , ( ), X [1, 2]:
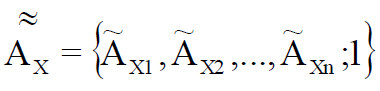 (4)
(4)
– , 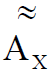 , – ( ) . – ( – ) [3, 9].
, – ( ) . – ( – ) [3, 9].
Re 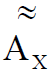 :
:
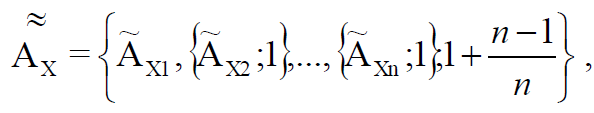 (5)
(5)
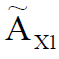 – X1,
– X1, 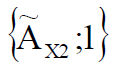 – X2 . .
– X2 . .
, – .
, , , . , , , .
, , .
: ( ), ( ), ( ).
X – , X :
 (6)
(6)
X1 – , X2 – , X3 – ,
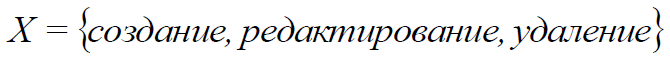 (7)
(7)
, ( – ), ( ), .
, X ( ), .
, () « » 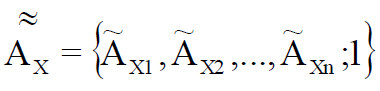 :
:
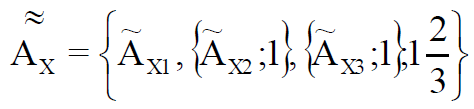 (8)
(8)
1,6(6) .
, ( , . use-case), ( , . test-case).
, , .
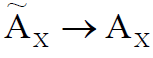 :
:
 (9)
(9)
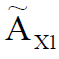 – X;
– X;
 – X, a ( ) 1;
– X, a ( ) 1;
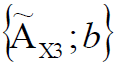 – X, b ( ) 1.
– X, b ( ) 1.
, ( ) , / .
Ux X , , ( -) , / , 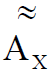 , :
, :
 (10)
(10)
n – X.
Tx X . , , :
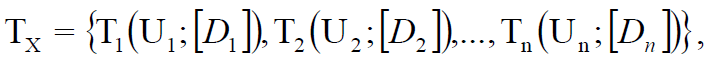 (11)
(11)
[D] – , n – X.
, . , .
, .
, « », , . , , .
« » , , .
- .., .., .., « ». .: – , 2014. – 88 .
- .., .., .., « ». .: – , 2014. – 122 .
- .., «: ». : , 2011. – 296 .
- ., « » / « ». .: «», 1974. – . 5 – 49.
- ., « ». .: , 2016. – 320 .
- .., « » / «», №54 (2/2008), http://www.delphis.ru/journal/article/fraktalnaya-matematika-i-priroda-peremen.
- ., « ». .: , 2002. – 656 .
- « : », . .., .. : - . . . -, 2003. – 24 .
- .., « ». .: -, 2017. – 622 .
- Zimmerman H. J. «Fuzzy Set Theory – and its Applications», 4th edition. Springer Seience + Business Media, New York, 2001. – 514 p.