Get best of the week

Julia e autômatos celulares


Hoje, faremos uma jornada colorida pelo mundo dos autômatos celulares, estudando simultaneamente alguns truques de sua implementação e também tentar entender o que está oculto por trás dessa beleza - um jogo curioso para uma mente ociosa ou um conceito filosófico profundo que ressoa em muitos modelos.


Para praticar e entender melhor, tente implementar os algoritmos a seguir. Bem, se a preguiça, ou apenas por interesse, você pode brincar com várias implementações:





— . , 0 1, , . . , . , . , 256 ( 8- ).



, .


:


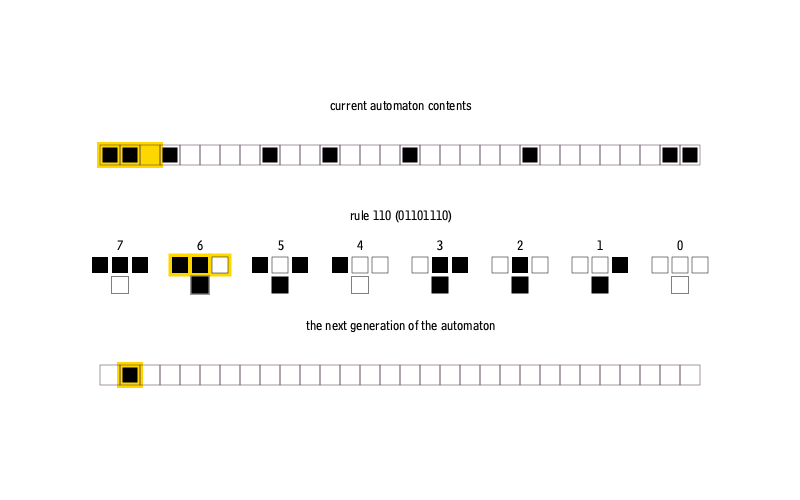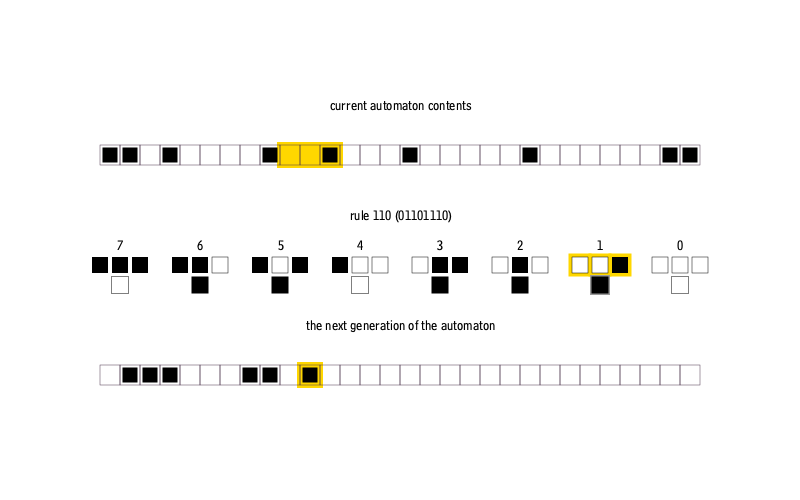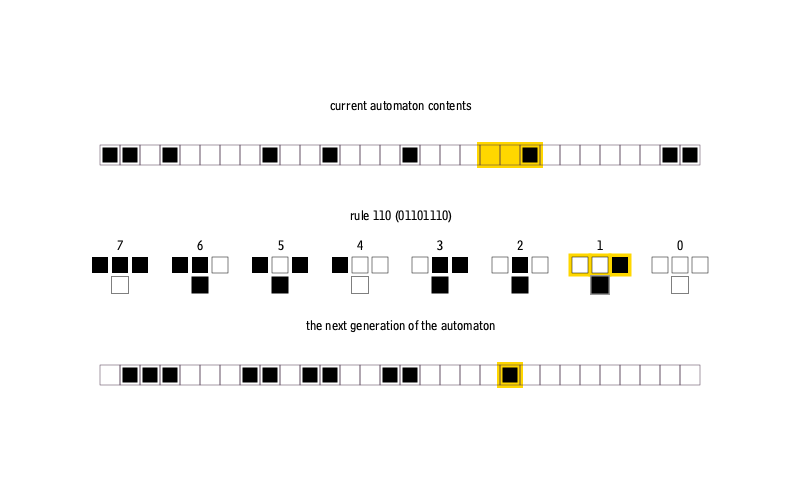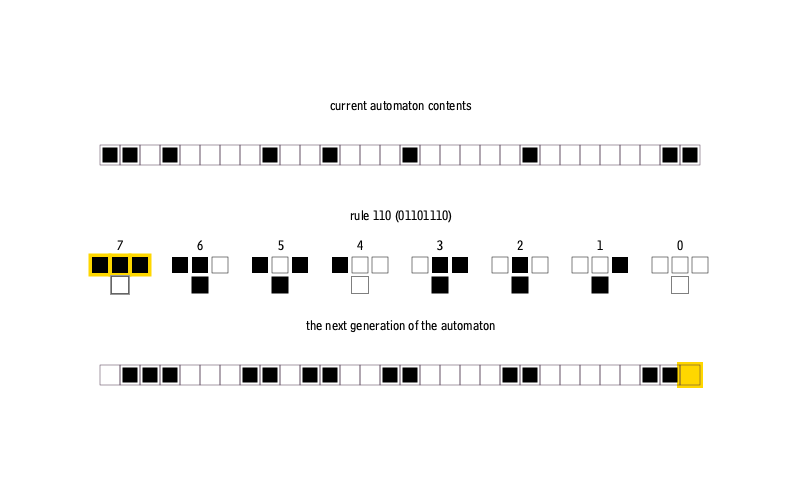
using Pkg
pkgs = ["Images", "ColorSchemes", "FFTW"]

for p in pkgs
    Pkg.add(p)
end

using Images, ColorSchemes, FFTW, LinearAlgebra: kron
using Random: bitrand
cd("C:\\Users\\User\\Desktop\\Mycop")

0 255 ( ). , . , , :


# , ,    
function cellauto( n::Int64, m::Int64, rule::Int64, s::Int64 = 1 )

    ptrn = digits(Bool, rule, base = 2, pad = 8)
    bt = [ bitstring(i)[end-2:end] for i = 0:7 ]
    d = Dict( bt[i] => ptrn[i] for i = 1:8 ) # 

    M = falses(n,m)
    M[1,m ÷ 2] = true
    #M[1,:] .= bitrand(m)
    for i = 1:n-1, j = 2:m-1
        key = "$(M[i, j-1]*1)$(M[i, j]*1)$(M[i, j+1]*1)"
        M[i+1,j] = d[key]
    end
    kron(M, ones(Int,s,s) ) #  
end

M0 = cellauto(100, 200, 30, 4)
Gray.( M0 )


30, . , , . , - : , … , . :


Arr = cellauto.(40, 40, [0:23;], 2);
Imgs = [ Gray.(a) for a in Arr ]
reshape(Imgs, 4,6)



, . :




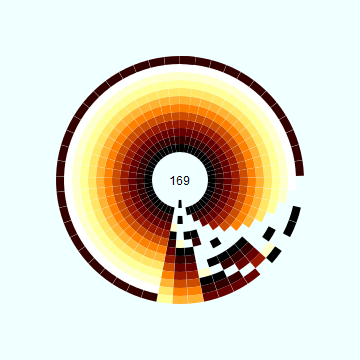
Luxor, .



"" — ( ) . , , : , ( ) .




: , , ( !) . , , , . . . , , , , , , . "" .



, , . , , .



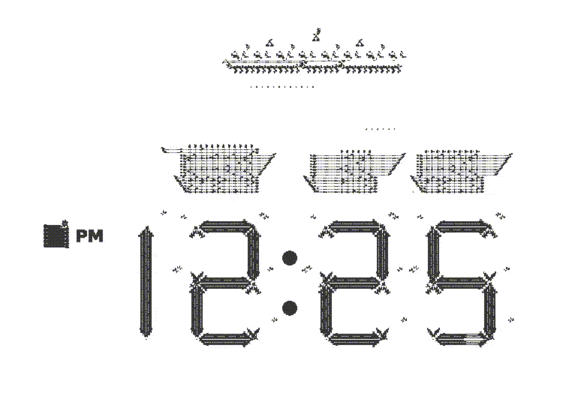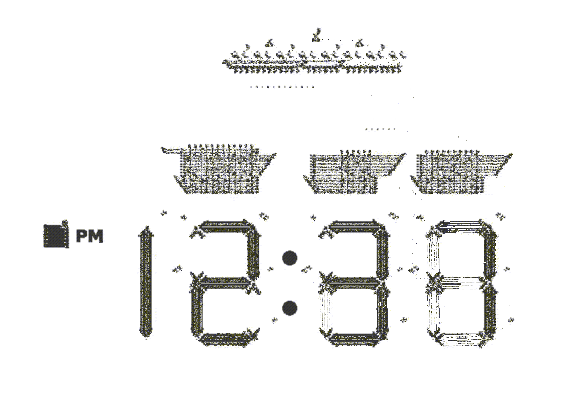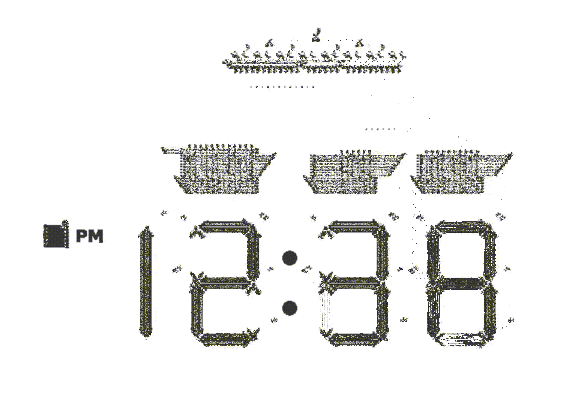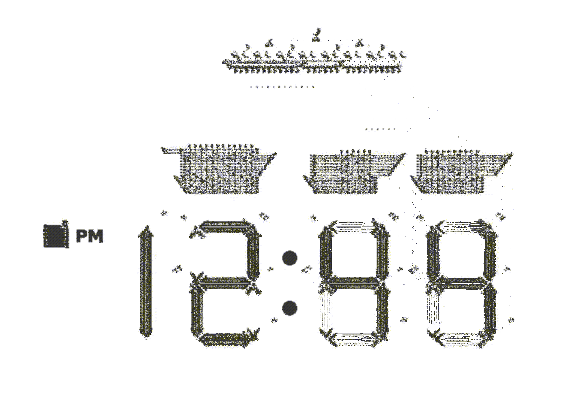
function makefilter(N::Int64)
    filter = zeros(Complex, N, N);
    IDX(x, y) = ( (x + N) % N ) + ( (y+N) % N ) * N + 1
        filter[IDX(-1, -1)] = 1. ;
        filter[IDX( 0, -1)] = 1. ;
        filter[IDX( 1, -1)] = 1. ;
        filter[IDX(-1,  0)] = 1. ;
        filter[IDX( 1,  0)] = 1. ;
        filter[IDX(-1,  1)] = 1. ;
        filter[IDX( 0,  1)] = 1. ;
        filter[IDX( 1,  1)] = 1. ;

    return fft( real.(filter) )
end

function fftlife(N = 16, steps = 100, dx = 0, glider = true)

    if glider
        state = falses(N, N)
        state[4,5] = state[5,6] = state[6,6] = true
        state[6,5] = state[6,4] = true
    else
        state = bitrand(N, N)
    end

    filter = makefilter(N)

    for i in 1:steps
        tmp = fft( real.(state) ) # forward
        tmp .*= filter

        summ = ifft(tmp) # reverse

        for i in eachindex(state)
            t = round( Int, real(summ[i]) ) >> dx
            state[i] = ( state[i] ? t == 2 || t == 3 : t == 3 )
        end
        save("KonLife_$(N)x$(N)_$i.png", kron( Gray.(state), ones(8,8) ) )
    end

end

fftlife(16, 60)


— , ( ). , "" .




:


df(x,t)dt=S(N(x,t),M(x,t))−f(x,t)S(n,m)=σn(σm(b1,b2),σm(d1,d2))M(x,t)=1πh2∫0≤|y|≤hf(x−y,t)dyN(x,t)=18πh2∫0≤|y|≤3hf(x−y,t)dy


1 0, , , .


function clamp(x)
    y = copy(x)
    y[x.>1] .= 1
    y[x.<0] .= 0
    y
end

function func_linear(X, a, b)
    Y = [ (x-a + 0.5b)/b for x in X ]

    Y[X.<a-0.5b] .= 0
    Y[X.>a+0.5b] .= 1
    return Y
end

function splat!(aa, ny, nx, ra)
    x = round(Int, rand()*nx ) + 1
    y = round(Int, rand()*ny ) + 1
    c = rand() > 0.5

    for dx = -ra:ra, dy = -ra:ra
        ix = x+dx
        iy = y+dy
        if ix>=1 && ix<=nx && iy>=1 && iy<=ny
            aa[iy,ix] = c
        end
    end
end

function initaa(ny, nx, ra)
    aa = zeros(ny, nx)
    for t in 0:((nx/ra)*(ny/ra))
        splat!(aa, ny, nx, ra);
    end
    aa
end

func_smooth(x::Float64, a, b)  = 1 / ( 1 + exp(-4(x-a)/b) ) 

sigmoid_a(x, a, ea) = func_smooth(x, a, ea)
sigmoid_b(x, b, eb) = 1 - sigmoid_a(x, b, eb)
sigmoid_ab(x, a, b, ea, eb) = sigmoid_a(x, a, ea) * sigmoid_b(x, b, eb)
sigmoid_mix(x, y, m, em) = x - x * func_smooth(m, 0.5, em) + y * func_smooth(m, 0.5, em)

function snm(N, M, en, em, b1, b2, d1, d2)

    [ sigmoid_mix( sigmoid_ab(N[i,j], b1, b2, en, en), 
                   sigmoid_ab(N[i,j], d1, d2, en, en), M[i,j], em ) 
                    for i = 1:size(N, 1), j = 1:size(N, 2) ]
end

function smoothlife(NX = 128, NY = 128, tfin = 10, scheme = 1)

    function derivative(aa)
        aaf = fft(aa)
        nf = aaf .* krf
        mf = aaf .* kdf
        n = real.(ifft(nf)) / kflr # irfft
        m = real.(ifft(mf)) / kfld
        2snm(n, m, alphan, alpham, b1, b2, d1, d2) .- 1
    end

    ra = 10
    ri = ra/3
    b = 1
    b1 = 0.257
    b2 = 0.336
    d1 = 0.365
    d2 = 0.551
    alphan = 0.028
    alpham = 0.147

    kd = zeros(NY,NX)
    kr = zeros(NY,NX)
    aa = zeros(NY,NX)

    x = [ j - 1 - NX/2 for i=1:NY, j=1:NX ]
    y = [ i - 1 - NY/2 for i=1:NY, j=1:NX ]

    r = sqrt.(x.^2 + y.^2)
    kd = 1 .- func_linear(r, ri, b) # ones(NY, NX)
    kr = func_linear(r, ri, b) .* ( 1 .- func_linear(r, ra, b) )
    #aa = snm (ix/NX, iy/NY, alphan, alpham, b1, b2, d1, d2);
    kflr = sum(kr)
    kfld = sum(kd)
    krf = fft(fftshift(kr))
    kdf = fft(fftshift(kd))

    #for td in 2 .^(10:-1:3)
    for td = 64

        aa = initaa(NY,NX,ra)
        dt = 1/td;
        l = 0
        nx = 0
        for t = 0:dt:tfin
# 1=euler  2=improved euler  3=adams bashforth 3  4=runge kutta 4
            if scheme==1

                aa += dt*derivative(aa)

            elseif scheme==2

                da = derivative(aa);
                aa1 = clamp(aa + dt*da)
                for h = 0:20
                    alt = aa1
                    aa1 = clamp(aa + dt*(da + derivative(aa1))/2)
                    if maximum(abs.(alt-aa1))<1e-8 
                        break
                    end
                end
                aa = copy(aa1)

            elseif scheme==3

                n0 = 1+mod(l,3)
                n1 = 1+mod(l-1,3)
                n2 = 1+mod(l-2,3)

                f = zeros(NY, NX, 3) # ?
                f[:,:,n0] = derivative(aa)
                if l==0
                    aa += dt*f[:,:,n0]
                elseif l==1
                    aa += dt*(3*f[:,:,n0] - f[:,:,n1])/2
                elseif l>=2
                    aa += dt*(23*f[:,:,n0] - 16*f[:,:,n1] + 5*f[:,:,n2])/12
                end

            elseif scheme==4

                k1 = derivative(aa)
                k2 = derivative(clamp(aa + dt/2*k1))
                k3 = derivative(clamp(aa + dt/2*k2))
                k4 = derivative(clamp(aa + dt*k3))
                aa += dt*(k1 + 2*k2 + 2*k3 + k4)/6

            end

            aa = clamp(aa)

            if t >= nx
                save("$(scheme)\\$(td)_$t.png", Gray.(kron(aa, ones(2, 2) ) ) )
                nx += 1;
            end

            l += 1;
        end

    end     # for td
end

@time smoothlife(256, 256, 20, 3)


, . , . .




— , , . — .



, , , :


  • — 90∘, , .
  • — 90∘, , .

rosetta code , :


function ant(width, height)
    y, x = fld(height, 2), fld(width, 2)
    M = trues(height, width)

    dir = im
    for i in 0:1000000
        x in 1:width && y in 1:height || break
        dir *= M[y, x] ? im : -im
        M[y, x] = !M[y, x]
        x, y = reim(x + im * y + dir)
        i%100==0 && save("LR//zLR_$i.png", Gray.( kron(M,ones(4,4) ) ) )
    end

    Gray.(M)
end

ant(100, 100)


, . — . !


:


function ant(width, height, comnds;
        steps = 10, cxema = reverse(ColorSchemes.hot), 
        savevery = 100, pixfactor = 20)

    ma3x2pix() = [ clrs[k%n+1] for k in M ]
      bigpix() = kron( ma3x2pix(), ones(Int64,m,m) )
    save2pix(i) = save("$(comnds)_$i.png", bigpix() )

    m = pixfactor
    n = length(comnds)
    colorsinscheme = length(cxema)
    M = zeros(Int64, height, width)
    y, x = fld(height, 2), fld(width, 2)

    st = colorsinscheme ÷ n
    clrs = [ cxema.colors[i] for i in 1:st:colorsinscheme ]

    dir = im
    for i in 0:steps
        x in 1:width && y in 1:height || (save2pix(i); break)
        j = M[y, x] % n + 1
        dir *= comnds[j] == 'L' ? -im : im
        M[y, x] += 1
        x, y = reim(x + im * y + dir)

        i % savevery==0 && save2pix(i)
    end
    ma3x2pix()
end

@time ant(16, 16, "LLRR", steps = 100, savevery = 1, pixfactor = 20)


, !




. , ? ?..


# http://rosettacode.org/wiki/Mandelbrot_set
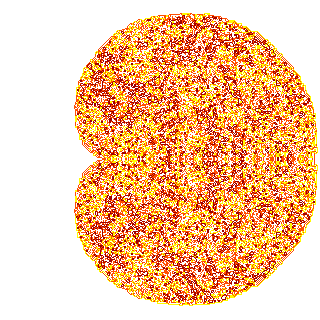
function hsv2rgb(h, s, v)
    c = v * s
    x = c * (1 - abs(((h/60) % 2) - 1) )
    m = v - c

    r,g,b =
        if h < 60
            (c, x, 0)
        elseif h < 120
            (x, c, 0)
        elseif h < 180
            (0, c, x)
        elseif h < 240
            (0, x, c)
        elseif h < 300
            (x, 0, c)
        else
            (c, 0, x)
        end

    (r + m), (b + m), (g + m)
end

function mandelbrot()

    w, h = 1000, 1000

    zoom  = 1.0
    moveX = 0
    moveY = 0

    img = Array{RGB{Float64}, 2}(undef,h, w)
    maxIter = 30

    for x in 1:w
        for y in 1:h
            i = maxIter
            c = Complex(
                (2*x - w) / (w * zoom) + moveX,
                (2*y - h) / (h * zoom) + moveY
            )
            z = c
            while abs(z) < 2 && (i -= 1) > 0
                z = z^2 + c
            end
            r,g,b = hsv2rgb(i / maxIter * 360, 1, i / maxIter)
            img[y,x] = RGB{Float64}(r, g, b)
        end
    end

    save("mandelbrot_set2.png", img)
end

mandelbrot()


:










— . :







, . (-), -, , , ! , !



. ,



, . ( - . )


. , — , : , , , ...



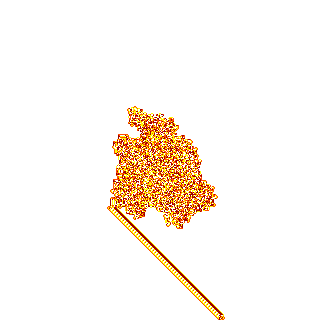
More articles:


All Articles