Um desejo excessivo de precisão começou a ter um efeito que nega a teoria do controle e a teoria dos sistemas, uma vez que leva ao fato de que a pesquisa nessa área se concentra naqueles e apenas nos problemas que podem ser resolvidos com precisão. Muitas classes de problemas importantes nos quais dados, objetivos e restrições são muito complexos ou mal definidos para permitir uma análise matemática precisa permaneceram e permanecem à margem apenas porque não podem ser interpretados matematicamente. L. Zade
Definição e características
No mundo, muito não se divide apenas em branco e preto, em verdade e verdade ... Uma pessoa usa muitos conceitos difusos para avaliar e comparar quantidades físicas, estados de objetos e sistemas em um nível aproximado e qualitativo. Portanto, qualquer um de nós é capaz de estimar a temperatura do lado de fora da janela, sem recorrer a um termômetro, e guiado apenas por nossos próprios sentimentos e uma escala de estimativas aproximadas ("nublado o suficiente para levar um guarda-chuva").
Mas uma avaliação qualitativa não possui a propriedade de aditividade inerente aos nossos números usuais; isto é, não podemos determinar o resultado das operações para estimativas aproximadas (“pequena quantidade de dinheiro” + “pequena quantidade de dinheiro”), em contraste com, por exemplo, números naturais (2 + 2). Não podemos determinar porque uma avaliação qualitativa depende fortemente do tomador de decisão, contexto e significado investido em um caso específico.
No entanto, no mundo existem quantidades suficientes que não somos capazes de avaliar com precisão por uma razão ou outra: o grau de ordem na sala, o "prestígio" do carro, a beleza de uma pessoa, a "semelhança" das coisas ... Mas eu quero trabalhar com elas como nos números usuais seria para tarefas de automação.
. 1964 .
.
( )  () U
() U )%20) ,
,  ,
,
%20) —
—  ,
, ![\ mu_A (u): U → [0; 1]](https://tex.s2cms.ru/svg/%20%5Cmu_A%20(u)%3AU%20%E2%86%92%5B0%3B1%5D%20) .
. %7D(%5Cmu_A%20(u)%20%2F%20u)%20%3D%20%5Cleft%5C%7B%20%20(%5Cmu_A(u)%20%2F%20u)%20%5Cright%5C%7D%20%20) .
.
U %20) ( ) u (-)
( ) u (-)  . , . - .
. , . - .
%20) ( . ), – . – U
( . ), – . – U  . , , .
. , , .
, %20%3D%20%5Cbegin%7Bcases%7D1%20%26%20u%20%5Csubseteq%20A%20%5C%5C0%20%26%20u%20%5Cnsubseteq%20A%20%5Cend%7Bcases%7D%20) , .
, .
, %20) :
:
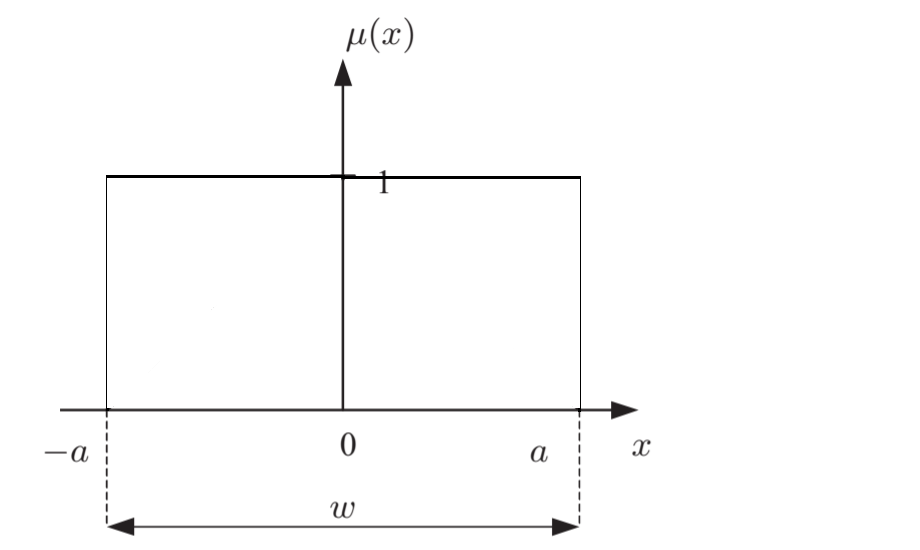
-a≤x≤a.
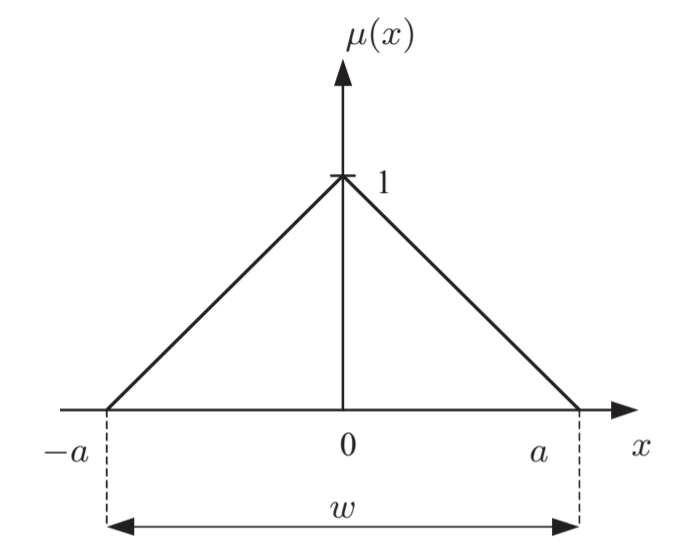
“ ”.
%3D%20%5Cfrac%7B(a-%7Cx%7C)%7D%7Ba%7D%2C%20%20-a%20%5Cleq%20x%20%5Cleq%20a%20)
 .
.
.
– , 1. 0.
, %20) 0.5, . -a/2 a/2.
0.5, . -a/2 a/2.
)%2Cu%20%5Csubseteq%20U%20) .
.
, 1, . – .
, , 0, .
, 1 .
2 %20)
%3E0%2C%20%20x%20%5Csubseteq%20X%20%5Cright%5C%7D%20) –
–  .
. 
 .
.
, x, %3D0%20) ; –
; – %7D%3D0%20) .
.
, , . :
- , ;
- , ;
- , , .
:  — U,
— U,  . , .
. , .
 ,
, %3D%20%5Cmu_B(x)%20) .
.
 ,
, %20%5Cleq%20%0A%20%5Cmu_B%20(x)%20) x.
x.
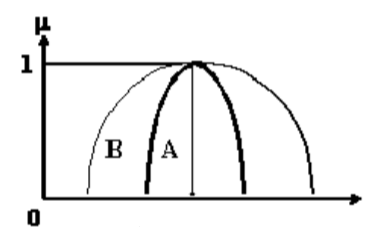
 ,
, %20%3D%20max%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cvee%20%5Cmu_B%20(x)%20) . (t– s–)
. (t– s–)
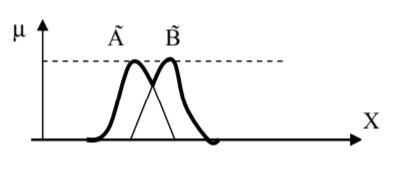
 ,
, %20%3D%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20) . ,
. , %20%3D%20%5Cmu_A(x)%20%5Cwedge%20%5Cmu_B%20(x)%20) . (t-)
. (t-)
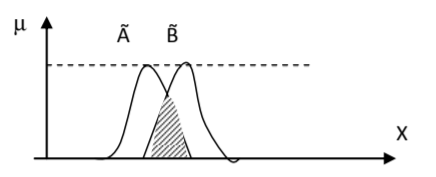
:
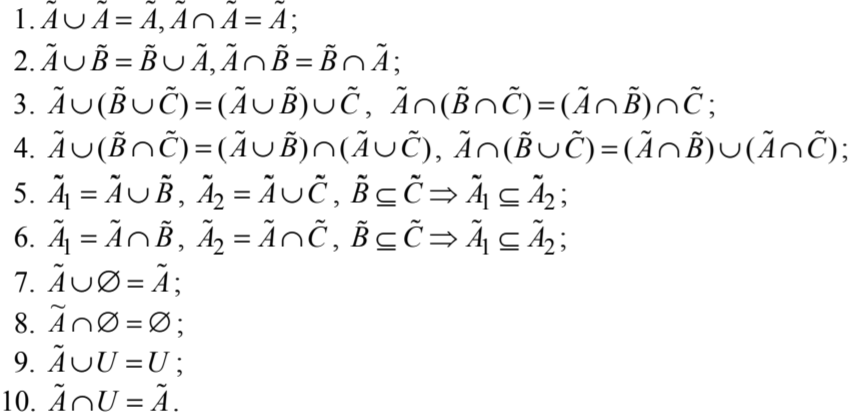
. , , . , min max .
 ,
, %20%3D%20%5Cmu_A(x)%20-%20%5Cmu_%7BA%20%5Ccap%20B%7D(x)%20%3D%20%5Cmu_A(x)%20-%20min%E2%81%A1%20(%5Cmu_A%20(x)%3B%20%5Cmu_B%20(x))%20%3D%20max(0%3B%20%5Cmu_A(x)%20-%20%5Cmu_B(x))%20) .
.

 . ,
. , %20%3D%201-%20%5Cmu_%7B%5Coverline%7BA%7D%7D(x)%20) .
.
. , , , (,  ). :
). :
α- . α-  ,
, %20%5Cgeq%20%5Calpha%20) .
.
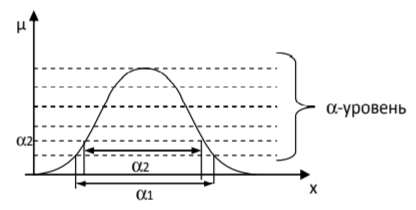
.  , M — .
, M — .
 ,
, %3D%20%5Cmu_A%5E%7B%5Cbeta%7D(x)%20) . :
. :
- β = 2 ( CON(A) ). , . , “ ” ;
- β = 0.5 ( DIL(A) ). , . “ ”.
.
%20%3D%20%5Cmu_A(x)%20*%20%5Cmu_B%20(x)%20) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cvee%200%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%201%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%201%5C%5C0%20%26%20%5Cend%7Bcases%7D%20) .
.
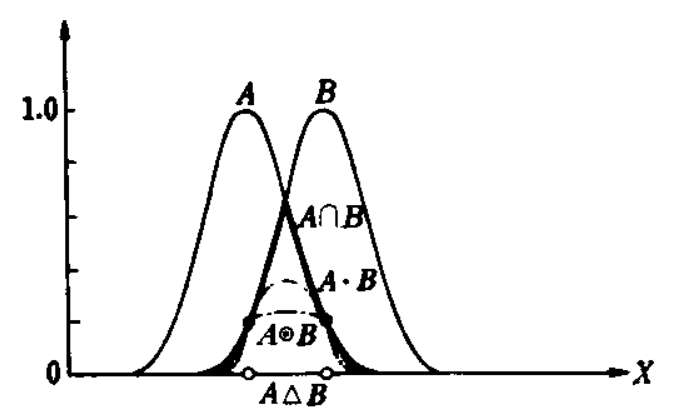
%20%3D%20%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%20%5Cmu_A(x)*%5Cmu_B(x)) .
.
%20%3D%20(%5Cmu_A(x)%20%2B%20%5Cmu_B(x)%20-%201)%20%5Cwedge%201%20) .
.
%20%3D%20%5Cbegin%7Bcases%7D%5Cmu_B(x)%20%26%20%5Cmu_A(x)%20%3D%200%5C%5C%5Cmu_A(x)%20%26%20%5Cmu_B(x)%20%3D%200%5C%5C1%20%26%20%5Cend%7Bcases%7D%20) .
.
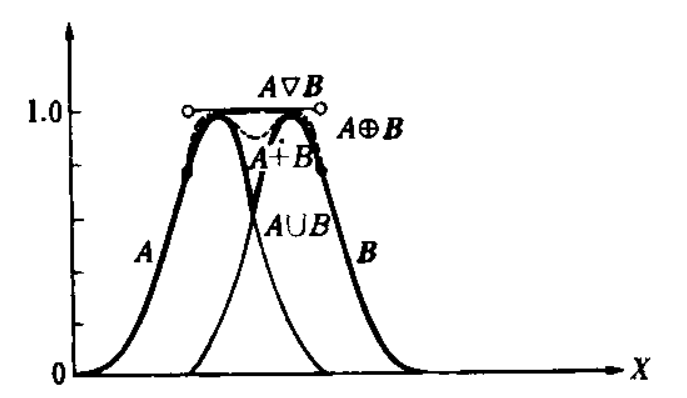
- – A B λ (1 — λ) ( A B). %20%3D%20%5Clambda%20*%20%5Cmu_A(x)%20%2B%20(1%20-%20%5Clambda)%20*%20%5Cmu_B(x)%20) .
.
, λ- :

?
, , . . , ( , ). 2 – .
, . , , , . : , .
, , . , .
, , , , , :
- 0 <= μ(x) <= 1;
- ( );
- A função e o conjunto de funções definidas devem ter uma diferenciação natural de conceitos representados por conjuntos vizinhos;
- Não deve haver lacunas no conjunto universal (ou limitado para consideração) ao qual nenhum conjunto está associado;
- Para conjuntos vizinhos, o máximo de um deve coincidir com o mínimo do outro, e o ponto de interseção de seus gráficos deve corresponder aos pontos de transição;
- e alguns outros específicos de tarefas.
embora existam situações excepcionais em que uma função deve ser determinada com base no contexto. A construção de tais funções é um tópico separado e bastante complicado.
E isso é tudo por hoje.