🚙 ☕️ 🦈 Como os tipos inteiros muito longos são implementados no Python? 👌🏾 ♉️ 🚴🏿

Uma tradução do artigo foi preparada especificamente para os alunos do curso Python Developer .

Quando você escreve em um idioma de baixo nível, como C, fica preocupado em escolher o tipo e os qualificadores de dados corretos para seus números inteiros, em cada etapa você analisa se será suficiente usá-lo simplesmente intou se você deseja adicionar longou até mesmo long double. No entanto, ao escrever código em Python, você não precisa se preocupar com essas coisas "secundárias", porque o Python pode trabalhar com números de integerqualquer tipo de tamanho.

Em C, se você tentar calcular 2 ²⁰⁰⁰⁰ usando a função interna powl, obterá a saída inf.

#include <stdio.h>
#include <math.h>

int main(void) {
  printf("%Lf\n", powl(2, 20000));
  return 0;
}

$ ./a.out
inf

Mas no Python, tornar isso mais fácil do que nunca é fácil:

>>> 2 ** 20000
39802768403379665923543072061912024537047727804924259387134 ...
...
... 6021 digits long ...
...
6309376

Deve ser óbvio que o Python está fazendo algo muito bonito, e hoje vamos descobrir o que ele faz para trabalhar com números inteiros de tamanho arbitrário!

Apresentação e Definição

Integer em Python, essa é uma estrutura C definida da seguinte maneira:

struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};

PyObject_VAR_HEADÉ uma macro, ela se expande para PyVarObject, que possui a seguinte estrutura:

typedef struct {
    PyObject ob_base;
    Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;

Outros tipos que possuem PyObject_VAR_HEAD:

PyBytesObject
PyTupleObject
PyListObject

Isso significa que um número inteiro, como uma tupla ou uma lista, tem um comprimento variável, e este é o primeiro passo para entender como o Python pode suportar o trabalho com números gigantes. Uma vez expandida, a macro _longobjectpode ser considerada como:

struct _longobject {
    PyObject ob_base;
    Py_ssize_t ob_size; /* Number of items in variable part */
    digit ob_digit[1];
};

Existem PyObjectalguns meta-campos na estrutura que são usados para a contagem de referência (coleta de lixo), mas, para falar sobre isso, precisamos de um artigo separado. O campo no qual focaremos isso ob_digite daqui a pouco ob_size.

Descriptografia `ob_digit`

ob_digitÉ uma matriz alocada estaticamente do tamanho da unidade do tipo digit (typedef uint32_t). Como essa é uma matriz, ob_digité principalmente um ponteiro para um número e, portanto, se necessário, pode ser aumentada usando a função malloc para qualquer comprimento. Dessa forma, o python pode representar e processar números muito longos.

Normalmente, em linguagens de baixo nível, como C, a precisão de números inteiros é limitada a 64 bits, no entanto, o Python suporta números inteiros de precisão arbitrária . Começando com o Python 3, todos os números são apresentados no formulário bignume são limitados apenas pela memória do sistema disponível.

Descriptografia `ob_size`

ob_sizearmazena o número de itens em ob_digit. O Python substitui e usa o valor ob_sizepara determinar o número real de elementos contidos na matriz para aumentar a eficiência da alocação de memória na matriz ob_digit.

Armazenamento

A maneira mais ingênua de armazenar números inteiros é armazenar um dígito decimal em um elemento da matriz, para que operações como adição e subtração possam ser realizadas de acordo com as regras da matemática do ensino fundamental.

Com essa abordagem, o número 5238 será salvo assim: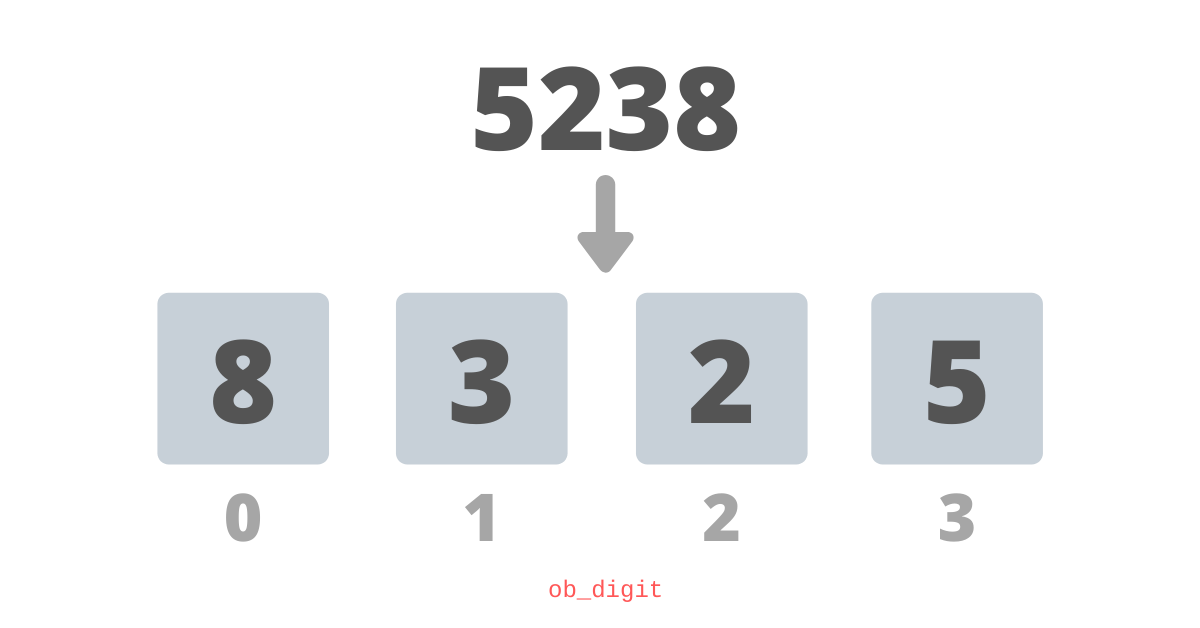

Essa abordagem é ineficiente, pois usaremos dígitos de até 32 bits (uint32_t) para armazenar um dígito decimal, que na verdade varia de 0 a 9 e pode ser facilmente representado com apenas 4 bits, pois, ao escrever algo tão versátil quanto python, o desenvolvedor do kernel deve ser ainda mais inventivo.

Então, podemos fazer melhor? Claro, caso contrário, eu não teria postado este artigo. Vamos dar uma olhada em como o Python armazena um número inteiro extra longo.

Caminho do Python

Em vez de armazenar apenas um dígito decimal em cada elemento da matriz ob_digit, o Python converte números do sistema numérico com base de 10 em números em um sistema com base de 2 ³⁰ e chama cada elemento como um dígito cujo valor varia de 0 a 2 ³⁰ - 1.

No sistema numérico hexadecimal, a base 16 ~ 2 ⁴ significa que cada "dígito" do número hexadecimal varia de 0 a 15 no sistema numérico decimal. No Python, da mesma forma, um “número” com uma base de 2 ³⁰ , o que significa que o número varia de 0 a 2 ³⁰ - 1 = 1073741823 em decimal.

Portanto, o Python efetivamente usa quase todo o espaço alocado de 32 bits por dígito, economiza recursos e ainda executa operações simples, como adição e subtração no nível matemático do ensino fundamental.

Dependendo da plataforma, o Python usa matrizes inteiras não assinadas de 32 bits ou matrizes inteiras não assinadas de 16 bits com dígitos de 15 bits. Para executar as operações que serão discutidas posteriormente, você precisa apenas de alguns bits.

Exemplo: 1152921504606846976

Como mencionado, para Python, os números são representados em um ^sistema base 2 ³⁰ , ou seja, se você converter 1152921504606846976 em um número base com 2 ³⁰ bases , obtém 100.

11529215046068464676 = 100 * 1152921504606846976 = 1 * (2 ³⁰) ² + 0 * (2 ³⁰ ) ¹ + 0 * (2 ³⁰ ) ⁰

Como o ob_digitdígito menos significativo é armazenado primeiro, ele é salvo como 001 como três dígitos.

A estrutura _longobjectpara esse valor conterá:

ob_size like 3
ob_digit como [0, 0, 1]

Eu criei uma demonstração REPL que irá mostrar como Python armazena um inteiro dentro de si, e também se refere a membros da estrutura, tais como ob_size, ob_refcountetc.

Operações Inteiras Longas

Agora que temos uma idéia clara de como o Python implementa números inteiros de precisão arbitrária, é hora de entender como várias operações matemáticas são executadas com eles.

Adição

Os números inteiros são armazenados "em números", o que significa que a adição é tão simples quanto na escola primária, e o código fonte do Python nos mostra que é assim que a adição é implementada. Uma função com um nome x_addem um arquivo longobject.cadiciona dois números.

...
    for (i = 0; i < size_b; ++i) {
        carry += a->ob_digit[i] + b->ob_digit[i];
        z->ob_digit[i] = carry & PyLong_MASK;
        carry >>= PyLong_SHIFT;
    }
    for (; i < size_a; ++i) {
        carry += a->ob_digit[i];
        z->ob_digit[i] = carry & PyLong_MASK;
        carry >>= PyLong_SHIFT;
    }
    z->ob_digit[i] = carry;
...

O trecho de código acima é obtido de uma função x_add. Como você pode ver, ele itera sobre um número por números e realiza a adição de números, calcula o resultado e adiciona hifenização.

Torna-se mais interessante quando o resultado da adição é um número negativo. O sinal ob_sizeé um número inteiro, ou seja, se você tiver um número negativo, ob_sizeserá um sinal de menos. O ob_sizemódulo de valor determinará o número de dígitos em ob_digit.

Subtração

Assim como a adição ocorre, a subtração também ocorre. Uma função com um nome x_subno arquivo longobject.csubtrai um número de outro.

...
    for (i = 0; i < size_b; ++i) {
        borrow = a->ob_digit[i] - b->ob_digit[i] - borrow;
        z->ob_digit[i] = borrow & PyLong_MASK;
        borrow >>= PyLong_SHIFT;
        borrow &= 1; /* Keep only one sign bit */
    }
    for (; i < size_a; ++i) {
        borrow = a->ob_digit[i] - borrow;
        z->ob_digit[i] = borrow & PyLong_MASK;
        borrow >>= PyLong_SHIFT;
        borrow &= 1; /* Keep only one sign bit */
    }
...

O trecho de código acima é obtido de uma função x_sub. Nele, você vê como ocorre a enumeração de números e a subtração é realizada, o resultado é calculado e a transferência é distribuída. De fato, é muito semelhante à adição.

Multiplicação

E, novamente, a multiplicação será implementada da mesma maneira ingênua que aprendemos nas lições da matemática no ensino fundamental, mas não é muito eficiente. Para manter a eficiência, o Python implementa o algoritmo Karatsuba , que multiplica dois números de n dígitos em etapas simples de O (n ^log₂³ ).

O algoritmo não é simples e sua implementação está além do escopo deste artigo, mas você pode encontrar a sua implementação em funções k_mul e k_lopsided_mulno arquivo longobject.c.

Divisão e outras operações

Todas as operações em números inteiros são definidas no arquivo longobject.c, são muito simples de encontrar e rastrear o trabalho de cada uma. Atenção: Um entendimento detalhado do trabalho de cada um deles levará tempo, portanto faça um pré-estoque com pipoca .

O Python pré - aloca um pequeno número de números inteiros na memória, variando de -5 a 256. Essa alocação ocorre durante a inicialização e, como não podemos alterar os números inteiros (imutabilidade), esses números pré-alocados são singleton e são referenciados diretamente em vez de serem alocados. Isso significa que toda vez que usamos / criamos um número pequeno, o Python, em vez de vendê-lo, simplesmente retorna uma referência ao número alocado anteriormente.

Essa otimização pode ser rastreada na macro IS_SMALL_INTe na função get_small_intc longobject.c. Portanto, o Python economiza muito espaço e tempo no cálculo de números inteiros comumente usados.

Este é o segundo artigo da série Python Internals. O primeiro artigo foi sobre como mudei minha versão do Python para torná-loambíguo . Isso ajudará você a dar os primeiros passos para entender o código fonte do Python e continuar o caminho para se tornar um desenvolvedor de kernel do Python.

Se você quiser ver mais artigos semelhantes, assine a minha newsletter e receba-os diretamente na sua caixa de entrada. Escrevo sobre engenharia, engenharia de sistemas e um pouco sobre programação toda sexta-feira. Envie- me um e- mail para @arpit_bhayani . Você pode encontrar meus artigos anteriores em @ arpitbhayani.me / blogs .

Isso é tudo. Vejo você no curso !

Como os tipos inteiros muito longos são implementados no Python?