Get best of the week

Trabalhamos com gráficos bidimensionais em JavaScript

Bom dia amigos

Criar animações realistas de processos físicos pode parecer uma tarefa assustadora, mas não é. Os algoritmos usados ​​para isso podem ser muito simples e, ao mesmo tempo, reproduzir com precisão fenômenos físicos como movimento, aceleração e gravidade (atração).

Deseja saber como esses algoritmos são implementados em JS?



Exemplos podem ser encontrados aqui .

O código fonte está aqui .

Movimento uniforme e acelerado


Vamos começar com o movimento.

Para um movimento uniforme, podemos usar o seguinte código:

function move(dt) {
    x += vx * dt
    y += vy * dt
}

Aqui x e y são as coordenadas do objeto, vx e vy são a velocidade do objeto nos eixos horizontal e vertical, respectivamente, dt (time delta - time delta) é o tempo entre duas marcas de timer, que em JS é igual a duas chamadas para requestAnimationFrame.

Por exemplo, se queremos mover um objeto localizado em um ponto com coordenadas 150, 50 para o sudoeste, podemos fazer o seguinte (uma marca de timer ou uma etapa):

x = 150 += -1 * 0.1 - > 149.9
y = 50 += 1 * 0.1 - > 50.1

Até o movimento é chato, então vamos acelerar o nosso objeto:

function move(dt) {
    vx += ax * dt
    vy += ay * dt
    x += vx * dt
    y += vy * dt
}

Aqui ax e ay são a aceleração ao longo dos eixos x e y, respectivamente. Usamos a aceleração para alterar a velocidade (vx / vy). Agora, se pegarmos o exemplo anterior e adicionarmos aceleração ao longo do eixo x (a oeste), obtemos o seguinte:

vx = -1 += -1 * 0.1 - > -1.1 // vx += ax * dt
vy = 1 += 0 * 0.1 - > 1 // vy += ay * dt
x = 150 += -1.1 * 0.1 - > 149.89 // x += vx * dt;     -0.01
y = 50 += 1 * 0.1 - > 50.1 // y += vy * dt

Gravidade


Aprendemos como mover objetos individuais. Que tal aprender a movê-los em relação um ao outro? Isso é chamado de gravidade ou gravidade. O que precisamos fazer para isso?

Aqui está o que queremos obter:



Primeiro, vamos lembrar de algumas equações do ensino médio.

A força aplicada ao corpo é calculada pela seguinte fórmula:
F = m * a ... a força é igual à massa vezes a aceleração
a = F / m ... a partir disso, podemos concluir que a força age no objeto com aceleração

Se aplicarmos isso a dois objetos em interação, obtemos o seguinte: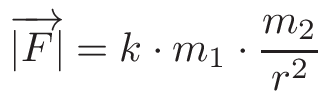



Parece complicado (pelo menos para mim), então vamos acertar. Nesta equação, | F | - esta é a magnitude da força, que é a mesma para os dois objetos, mas dirigida em direções opostas. Os objetos são representados pelas massas m_1 e m_2. k é a constante gravitacional er é a distância entre os centros de massa dos objetos. Ainda não está claro? Aqui está uma ilustração:



se queremos fazer algo interessante, precisamos de mais de dois objetos.



Nesta imagem, vemos dois objetos laranja atraindo preto com as forças F_1 e F_2, no entanto, estamos interessados ​​na força resultante F, que podemos calcular da seguinte forma:

  • primeiro calculamos as forças F_1 e F_2 usando a fórmula anterior:
  • então traduza tudo em vetores:

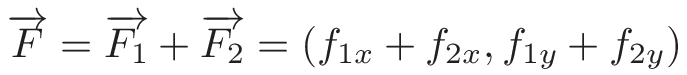
Ótimo, temos todos os cálculos necessários. Como podemos traduzir isso em código? Não vou aborrecê-lo com as etapas intermediárias e darei imediatamente o código finalizado com comentários. Se você precisar de mais informações, pode me escrever, responderei a todas as suas perguntas.

function moveWithGravity(dt, o) { // o -  ,    
    for (let o1 of o) { //   ()   
        o1.fx = 0
        o1.fy = 0
    }

    for (let [i, o1] of o.entries()) { //    
        for (let [j, o2] of o.entries()) {
            if (i < j) { //            
                let dx = o2.x - o1.x //     
                let dy = o2.y - o1.y
                let r = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2))
                if (r < 1) { //     0
                    r = 1
                }

                //     ; k = 1000
                let f = (1000 * o1.m * o2.m) / Math.pow(r, 2)
                let fx = f * dx / r
                let fy = f * dy / r
                o1.fx += fx //   
                o1.fy += fy
                o2.fx -= fx //      
                o2.fy -= fy
            }
        }
    }

    for (let o1 of o) { //    ...
        let ax = o1.fx / o1.m // 
        let ay = o1.fy / o1.m

        o1.vx += ax * dt // 
        o1.vy += ay * dt

        o1.x += o1.vx * dt // 
        o1.y += o1.vy * dt
    }
}

Choque


Corpos em movimento às vezes colidem. De uma colisão, os objetos são empurrados por outros ou alguns objetos se refletem nos outros. Primeiro



, vamos falar sobre empurrar: Primeiro, precisamos determinar que houve uma colisão:

class Collision {
    constructor(o1, o2, dx, dy, d) {
        this.o1 = o1
        this.o2 = o2

        this.dx = dx
        this.dy = dy
        this.d = d
    }
}

function checkCollision(o1, o2) {
    let dx = o2.x - o1.x
    let dy = o2.y - o1.y
    let d = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2))
    if(d < o1.r + o2.r){
        return {
            collisionInfo: new Collision(o1, o2, dx, dy, d),
            collided: true
        }
    }
    return {
        collisionInfo: null,
        collided: false
    }
}

Declaramos uma classe Collision que representa dois objetos em colisão. Na função checkCollision, primeiro calculamos a diferença entre as coordenadas xey dos objetos e depois calculamos a distância real d. Se a soma dos raios dos objetos for menor que a distância entre eles, houve uma colisão desses objetos - retorne o objeto Collision.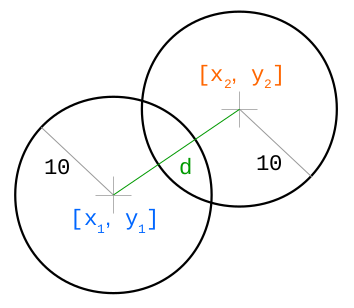



Em seguida, precisamos determinar a direção do deslocamento e sua magnitude (magnitude):
n_x = d_x / d ... este é o vetor
n_y = d_y / d

s = r_1 + r_2 - d ... essa é a "magnitude" da colisão (veja a figura abaixo)



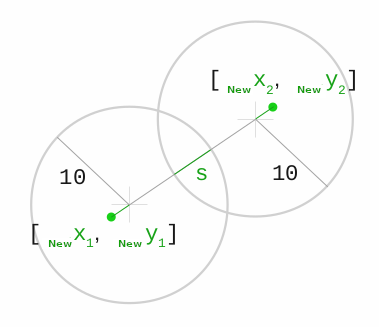Em JS, pode parecer Assim:

function resolveCollision(info){ // "info" -   Collision   
    let nx = info.dx / info.d //  
    let ny = info.dy / info.d
    let s = info.o1.r + info.o2.r - info.d //   
    info.o1.x -= nx * s/2 //       
    info.o1.y -= ny * s/2
    info.o2.x += nx * s/2 //      
    info.o2.y += ny * s/2
}

Pulo


A parte final do quebra-cabeça é a implementação do salto de um objeto de outro em uma colisão. Não darei todos os cálculos matemáticos, pois isso tornará o artigo muito longo e chato, limitarei-me ao fato de mencionar a lei da conservação do momento e a lei da conservação de energia, que ajudam a chegar à seguinte fórmula mágica:

k = -2 * ((o2.vx - o1.vx) * nx + (o2.vy - o1.vy) * ny) / (1 / o1.m + 1 / o2.m) ... * Magia *

Como podemos usar a magia k? Sabemos em que direção os objetos se moverão, mas não sabemos a que distância. Isso é k. É assim que o vetor (z) é calculado, mostrando para onde os objetos devem se mover:





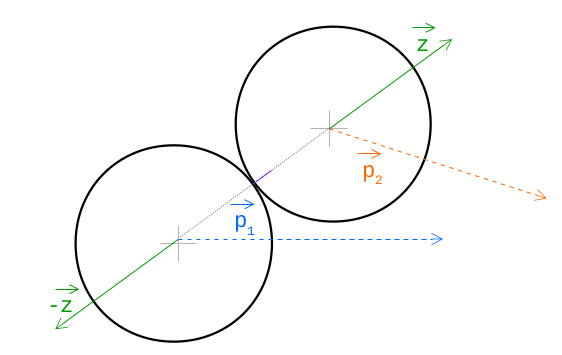O código fica assim:

function resolveCollisionWithBounce(info){
    let nx = info.dx / info.dy
    let ny = info.dy / info.d
    let s = info.o1.r + info.o2.r - info.d
    info.o1.x -= nx * s/2
    info.o1.y -= ny * s/2
    info.o2.x += nx * s/2
    info.o2.y += ny * s/2

    // ...
    let k = -2 ((info.o2.vx - info.o1.vx) * nx + (info.o2.vy - info.o1.vy) * ny) / (1/info.o1.m + 1/info.o2.m)
    info.o1.vx -= k * nx / info.o1.m //   ,   "k"   "s/2"  "m"
    info.o1.vy -= k * ny / info.o1.m
    info.o2.vx += k * nx / info.o2.m
    info.o2.vy += k * ny / info.o2.m
}

Conclusão


O artigo tem muitas equações, mas a maioria é muito simples. Espero que este artigo tenha ajudado um pouco a entender como os fenômenos e processos físicos são implementados no JS.

More articles:


All Articles