🙅🏼 👲🏽 🤛🏿 Visualização de linhas de tensão e movimentos de cargas eletrostáticas, simulação de movimento planetário do sistema solar 🥐 🏔️ 👼🏽

Olá, hoje eu quero oferecer uma ajuda visual para modelar alguns processos físicos e mostrar como obter belas imagens e animações. Cuidado com muitas fotos.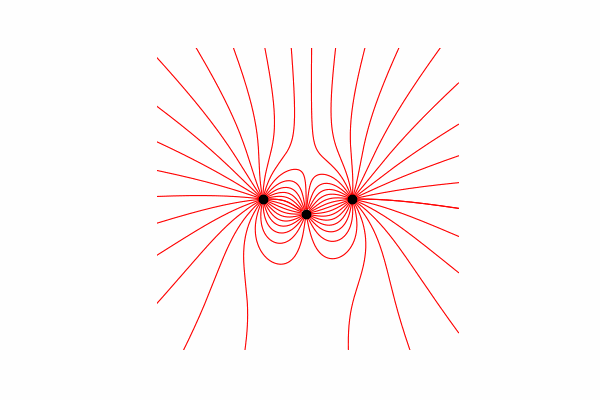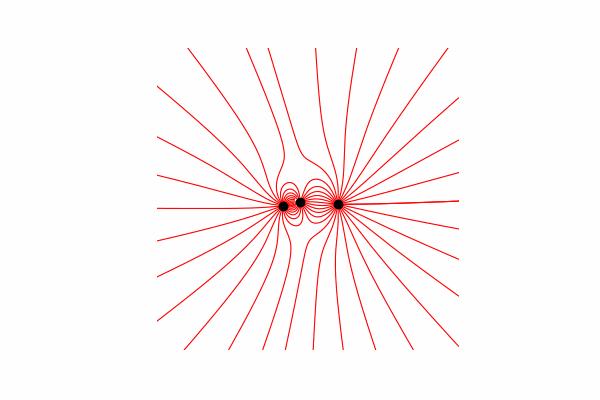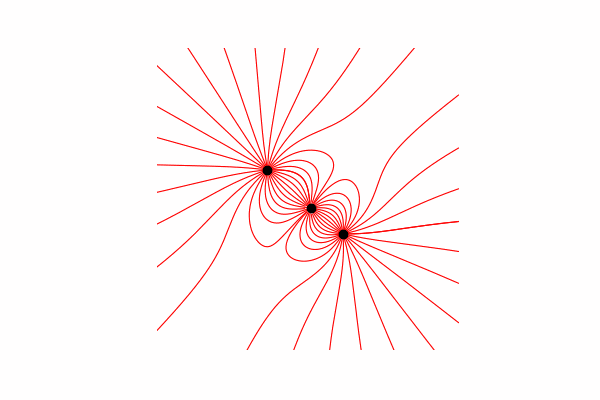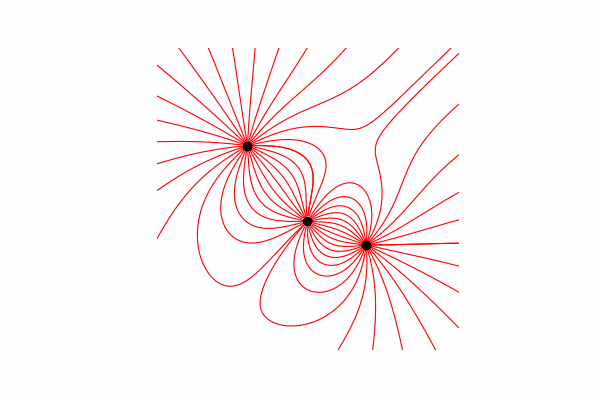

Todo o código pode ser encontrado no google colab .

Teoria

Primeiro, precisamos de um pequeno mínimo teórico sobre esse tópico. Vamos começar entendendo o que são linhas de tensão e como contá-las. De fato, essas linhas são a fusão de muitos vetores de tensão, que podem ser calculados da seguinte maneira: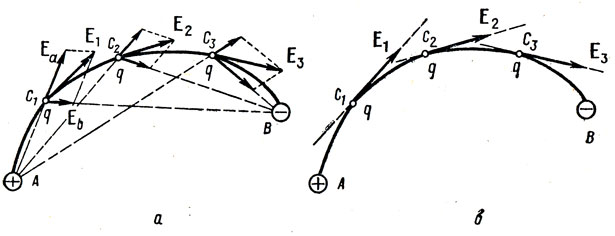

E = \frac{k * | q |}{r^{2}}

$E=\frac{k*|q|}{r^2}$ .

imagem

Método de cálculo E

Calculei o vetor de tensão através da semelhança de triângulos, obtendo assim projeções nos eixos xey y dx e dy, respectivamente.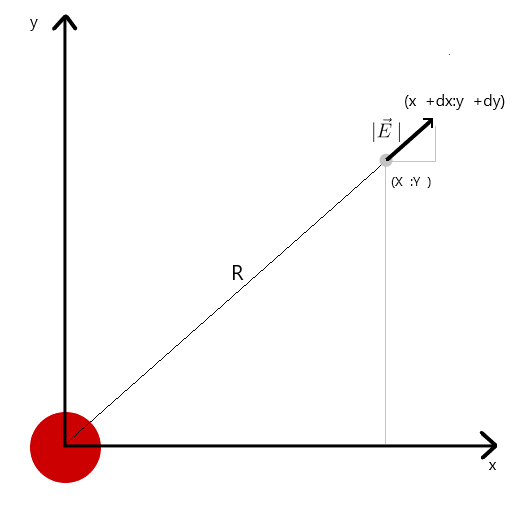

Da semelhança, segue-se que o raio do vetor da carga até o ponto no espaço re comprimento do vetor de intensidade E é igual à razão das projeções desses vetores (x1 e dx, respectivamente)

\frac{R}{E} = \frac{x}{d x} = \frac{y}{d y}

$\frac{R}{E}=\frac{x}{dx}=\frac{y}{dy}$ . Fórmula do vetor resultante

\vec{E} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{E}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{E}}_{i} |}{R_{i}} \end{matrix})

$\vec{E}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{E}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{E}_i|}{R_i} \end{array}\right) \qquad$
com esse conhecimento, obtemos o primeiro resultado.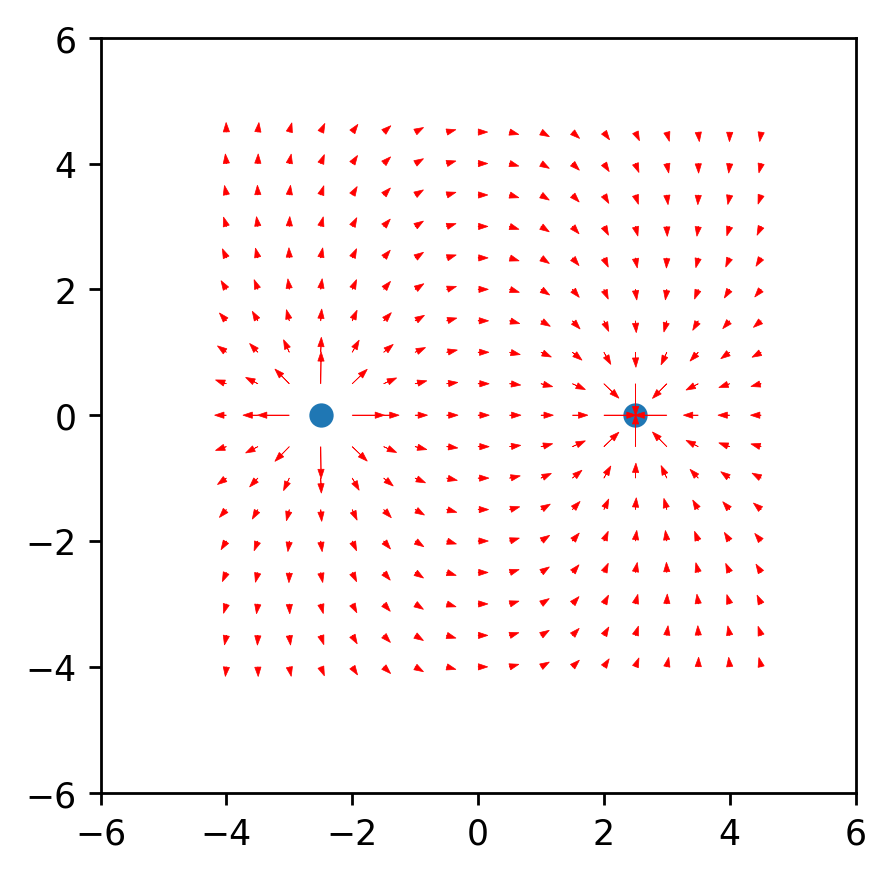

Função de cálculo de projeção

def E(q_prop, xs, ys, nq): #q_prop=[[xq1, yq1, q1, mq1, vxq1, vyq1], [xq2, yq2, q2, mq2, vxq2, vyq2] ... ] 
    l=1
    k=9*10**9
    Ex=0
    Ey=0
    c=0
    for c in range(len(q_prop)):#                
        q=q_prop[c]
        r=((xs-q[0])**2+(ys-q[1])**2)**0.5
        dEv=(k*q[2])/r**2
        dEx=(xs-q[0])*(dEv/r)*l
        dEy=(ys-q[1])*(dEv/r)*l

        Ex+=dEx
        Ey+=dEy
    return Ex, Ey

Método de construção de linha

Primeiro, você precisa decidir sobre o ponto inicial e final de onde a linha e o documento irão. O começo são pontos em um círculo com um raio r ao redor da carga, e os pontos finais não estão mais do que r separados das cargas.

código para pontos de partida

theta = np.linspace(0, 2*np.pi, n)
mask=q_prop[ q_prop[:,2]>0 ]#    
for cq in range(len(mask)):
    qmask=mask[cq]
    xr = r_q*np.cos(theta)+qmask[0]# -    
    yr = r_q*np.sin(theta)+qmask[1]#

Portanto, vale a pena dizer que as linhas são construídas apenas a partir de cargas positivas.

E, finalmente, a construção de linhas. Para isso, construímos a linha do vetor de tensão a partir do ponto inicial, atualizamos o ponto inicial no final da linha construída e repetimos até que as condições finais mencionadas acima sejam atingidas.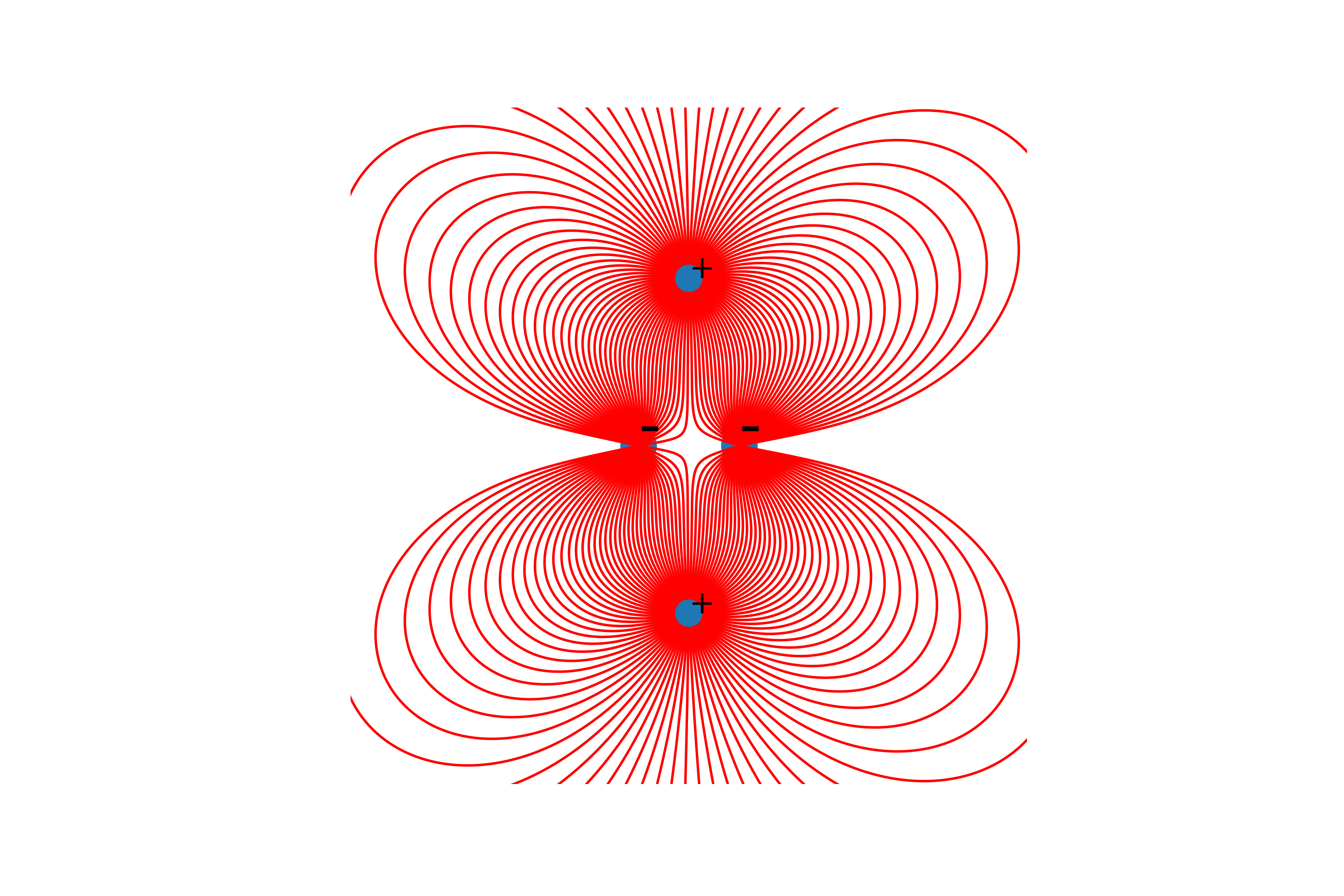

função de cálculo de coordenadas de linha

def Draw(size, q_prop,r_q, n):
  
  linen=np.empty((np.count_nonzero(q_prop[:,2]>0),n, 2000000), dtype=np.float64)
  linen[:] = np.nan
  theta = np.linspace(0, 2*np.pi, n)
  mask=q_prop[ q_prop[:,2]>0 ][ q_prop[q_prop[:,2]>0][:,3]==1 ]
  for cq in range(len(mask)):
    qmask=mask[cq]
    x11 = r_q*np.cos(theta)+qmask[0]
    x22 = r_q*np.sin(theta)+qmask[1]
    for c in range(len(x11)):

      xs=x11[c]
      ys=x22[c]

      lines=np.empty((2,1000000), dtype=np.float64)
      lines[:]=np.nan
      stop=0
      nnn=0
      
      lines[0][nnn]=xs
      lines[1][nnn]=ys
      while  abs(xs)<size+2 and abs(ys)<size+2: 
        nnn+=1

        for cq1 in range(len(q_prop)):
          q=q_prop[cq1]
          if ((ys-q[1])**2+(xs-q[0])**2)**0.5<r_q/2 :
            stop=1
            break
        if stop==1:
          break
        dx, dy = E1(q_prop,xs,ys)

        xs+=dx
        ys+=dy
        lines[0][nnn]=xs
        lines[1][nnn]=ys
       
      linen[cq,c,:]=lines.reshape(-1)

  return linen

Interação entre cobranças

Para refletir sua interação, é necessário alterar suas coordenadas e velocidade após cada pequeno tempo dt.

x + = \frac{E_{x} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{x} \cdot d t

$x+=\frac{E_x \cdot q \cdot dt^2}{2\cdot m} + v_x\cdot dt$

y + = \frac{E_{y} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{y} \cdot d t

$y+=\frac{E_y \cdot q \cdot dt^2}{2\cdot m} + v_y \cdot dt$

v_{x} + = \frac{E_{x} \cdot q \cdot d t}{m}

$v_x+= \frac{E_x \cdot q \cdot dt}{ m}$

v_{y} + = \frac{E_{y} \cdot q \cdot d t}{m}

$v_y+= \frac{E_y \cdot q \cdot dt}{ m}$

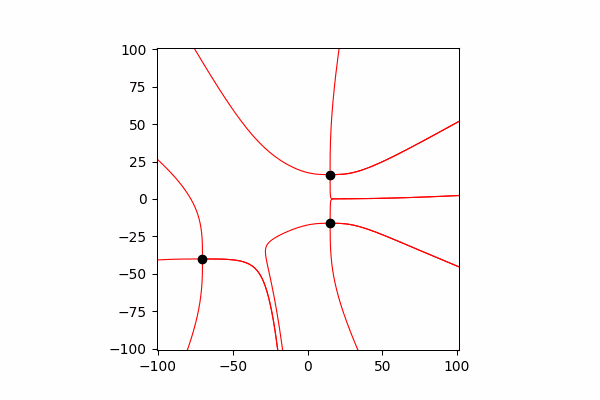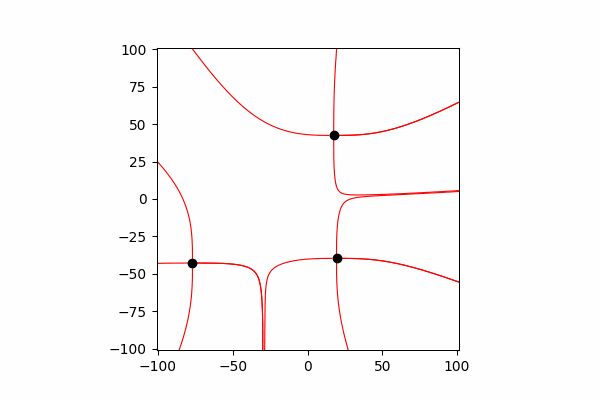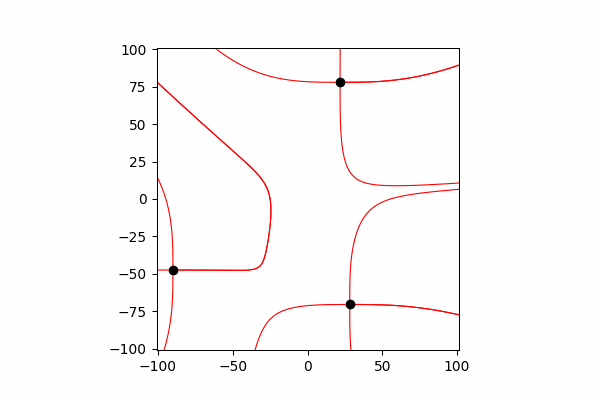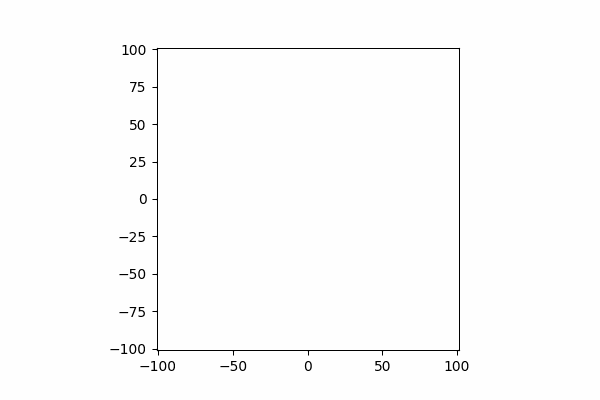
Função para atualizar coordenadas e projeções de velocidades de carga

def Update_all(q_prop):
  vx=0
  vy=0
  x=0
  y=0
  q_prop_1=np.copy(q_prop)
  for c in range(len(q_prop)):#         
    xs=q_prop[c][0]
    ys=q_prop[c][1]
    q =q_prop[c][2]
    m =q_prop[c][3]
    vx=q_prop[c][4]
    vy=q_prop[c][5]
    Ex, Ey= E(q_prop, xs, ys, c)

    x=(((Ex*q)/m)*dt**2)/2+vx*dt+xs
    y=(((Ey*q)/m)*dt**2)/2+vy*dt+ys
    vx+=((Ex*q)/m)*dt
    vy+=((Ey*q)/m)*dt
    #print(q_prop[c]-[x,y,q,m,vx,vy])
    q_prop_1[c]=[x,y,q,m,vx,vy]
  
  return q_prop_1#

Gravidade

Com base no código existente, escrevi um simulador que reflete os movimentos dos corpos sob a influência da gravidade. As alterações no código são principalmente para a função de tensão, pois a aceleração agora será considerada usando uma fórmula semelhante.

g = \frac{G * m}{r^{2}}

$g=\frac{G*m}{r^2}$

\vec{g} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{g}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{g}}_{i} |}{R_{i}} \end{matrix})

$\vec{g}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{g}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{g}_i|}{R_i} \end{array}\right) \qquad$

Os planetas começam no eixo x à distância do periélio e à velocidade do periélio. Todos os valores dos planetas e do sol (massa, distância, extremidades) do diretório.

Animação para os 4 primeiros planetas + sol.

À espera de críticas e sugestões. Tchau.

Visualização de linhas de tensão e movimentos de cargas eletrostáticas, simulação de movimento planetário do sistema solar

Teoria

Método de cálculo E

Método de construção de linha

Interação entre cobranças

Gravidade

More articles: