Penilaian Kualitas Clustering: Properti, Metrik, Kode GitHub

Clustering adalah hal yang sangat ajaib: mengubah sejumlah besar data yang tidak terstruktur menjadi kumpulan cluster yang berpotensi terlihat, analisis yang memungkinkan kita untuk menarik kesimpulan tentang konten data ini.

Ada banyak aplikasi untuk metode pengelompokan. Misalnya, kami mengelompokkan kueri penelusuran untuk meningkatkan kemampuan generalisasi algoritme peringkat: statistik apa pun yang dihitung dari grup kueri serupa lebih dapat diandalkan daripada statistik yang sama yang dihitung untuk satu kueri terpisah. Clustering memungkinkan Anda untuk meningkatkan kualitas kueri dengan formulasi yang jarang ditemui. Contoh jelas lainnya adalah Yandex.News, yang secara otomatis menghasilkan berita.

Kembali pada tahun 2013, saya beruntung dapat berpartisipasi dalam pengembangan algoritma pengelompokan yang sangat kompleks. Itu perlu untuk mengelompokkan ratusan ribu objek dengan kualitas sangat tinggi dan melakukannya dengan cepat: dalam puluhan detik pada satu mesin. Langkah pertama adalah membangun sistem penilaian kualitas, dan dalam artikel ini saya akan membicarakannya.

, , , .

, : , , , /- . , . — .

1.

, . .

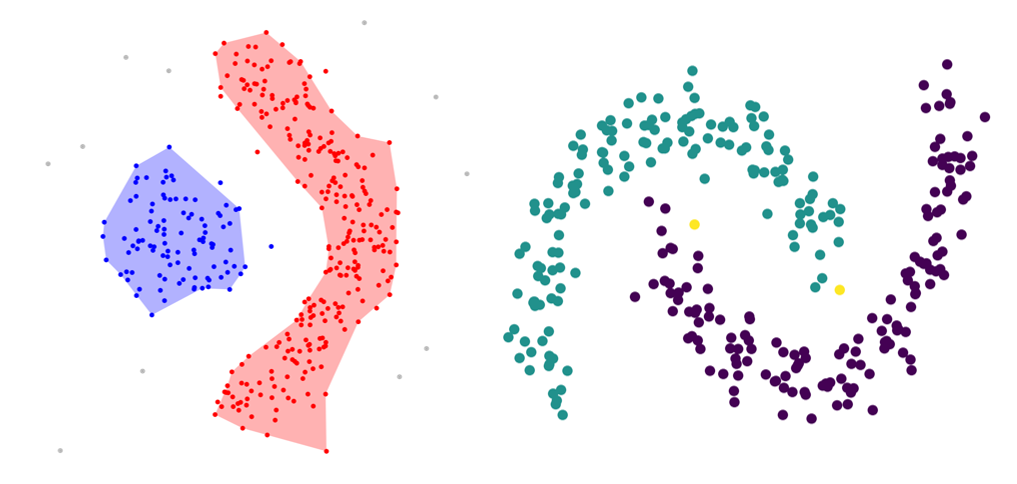
, . Amigo et. al, 2009. A comparison of Extrinsic Clustering Evaluation Metrics based on Formal Constraints , , .

1.1. Cluster Homogeneity,

.

1.2. Cluster Completeness,

, . .

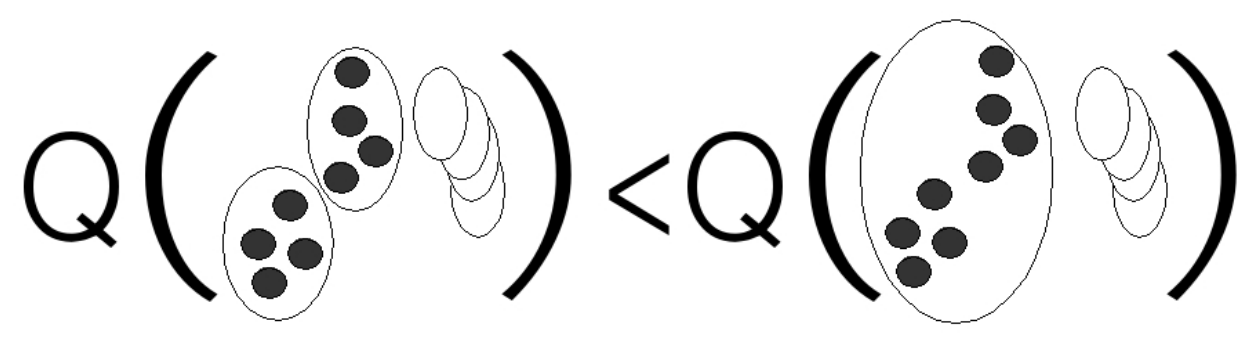
1.3. Rag Bag

: , , («»), . , , , .

, . , . «» : , .

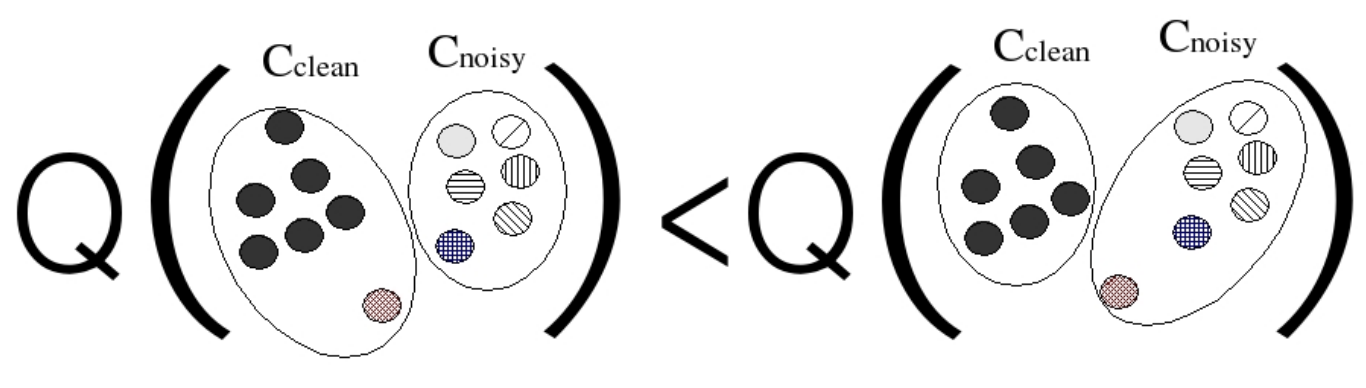
1.4. Size vs Quantity

.

2.

.

$$$D=\{d_1,...,d_N\}$. . , $$$E \subseteq 2^D$ — ,

$$

$$\forall e_1, e_2 \in E:(e_1 \cap e_2 \ne \emptyset) \Leftrightarrow (e_1 = e_2)$$

: . , .

, : $$$T=\{t_1,...,t_n\}$ $$$C=\{c_1,...,c_m\}$. $$$t(d)$ $$$c(d)$ , , , $$$d$.

2.1. , ()

. , . , .

. 3 («»), 3 («») 2 («»). : «» , «» «».

$$$8 \cdot 8 = 64$ , :
— $$$3 \cdot 3 + 3 \cdot 3 + 2 \cdot 2 = 22$ ;
— $$$64 - 22 = 42$ .

«» «» , - «» .

, :
— $$$TP = 18$ ;
— $$$FP = 6$ , ;
— $$$TN = 36$ ;
— $$$FN = 4$ , .

, :

$$

$$P = TP / (TP + FP) = 0.75$$

$$

$$R = TP / (TP + FN) = 0.82$$

$$

$$F_1 = \frac{2PR}{P + R} = 0.78$$

, : .

. , : .

pairwise- — . - pairwise- .

2.2. ,

:

$$

$$P(c, t) = \frac{ | c \cap t | }{| c |}$$

$$

$$R(c, t) = \frac{ | c \cap t | }{| t |}$$

: «» (y) «» (v). 25 10 . 25/35, — 10/35. . , 30 12 , 25/30, — 10/12.

: , . :

$$

$$P(c, t) = R(t, c)$$

F-:

$$

$$F_1(c, t) = \frac{2\cdot P(c, t) \cdot R(c,t)}{ P(c, t) + R(c,t) }$$

. «» , Purity:

$$

$$Purity = \sum_{i=1}^{m}{\frac{|c_i|}{m}{\max_{1 \le j \le n}{P(c_i, t_j)}}}$$

, :

$$

$$IversePurity = \sum_{j=1}^{n}{\frac{|t_j|}{n}{\max_{1 \le i \le m}{P(c_i, t_j)}}}$$

$$$Purity$ , . $$$IversePurity$ — . , ? , . :

$$

$$|c_2| \approx |t_2| \gg |t_1| \gg |c_1|$$

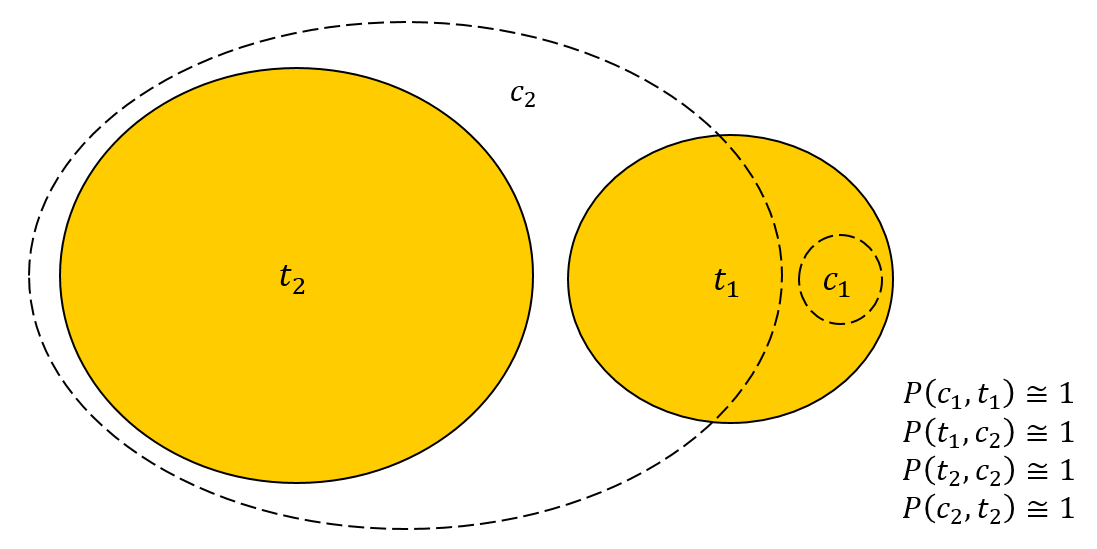
$$$|c_2| = 1000$, $$$|c_1| = 2$, $$$|t_1| = 20$, $$$|t_2| = 982$. $$$c_1$ $$$t_1$, :

$$

$$|c_1 \cap t_1| = 2, |c_1 \cap t_2| = 0,$$

$$

$$|c_2 \cap t_1| = 18, |c_2 \cap t_2| = 982$$

:

$$

$$P(c_1, t_1) = |c_1 \cap t_1| / |c_1| = 2/2 = 1$$

$$

$$P(c_2, t_2) = |c_2 \cap t_2| / |c_2| = 982/1000 = 0.982$$

$$

$$P(t_1, c_2) = |t_1 \cap c_2| / |t_1| = 18/20 = 0.9$$

$$

$$P(t_2, c_2) = |c_2 \cap t_2| / |t_2| = 982/982 = 1$$

, Purity InversePurity . :

$$

$$Purity =0.9982$$

$$

$$IversePurity = 0.9823$$

, $$$t_1$ . , . . Purity $$$t_1$ $$$c_1$, InversePurity — $$$c_2$. !

F-:

$$

$$F = \sum_{j=1}^{n}{\frac{|t_j|}{n}{\max_{1 \le i \le m}{F(c_i, t_j)}}}$$

, , . , , , .

2.3. BCubed-

. , . , , ? ?

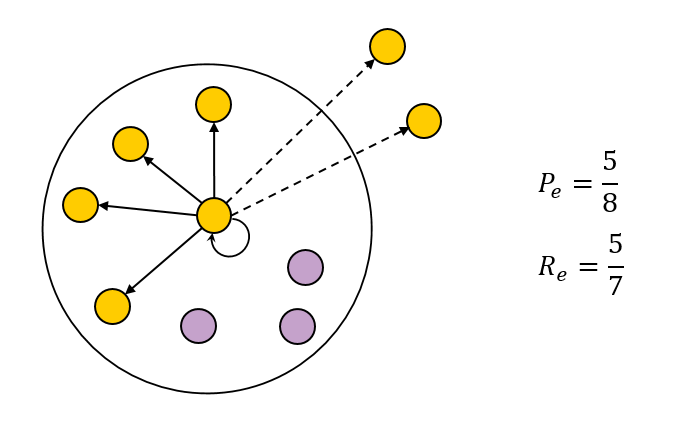
, BCubed- . :

$$

$$BCP(d) = \frac{|c(d) \cap t(d)|}{|c(d)|}$$

$$

$$BCR(d) = \frac{|c(d) \cap t(d)|}{|t(d)|}$$

:

$$

$$BCP = \frac{1}{N}\sum_{d \in D}{BCP(d)}$$

$$

$$BCR = \frac{1}{N}\sum_{d \in D}{BCR(d)}$$

BCubed Precision Cluster Homogeneity Rag Bag, BCubed Recall — Cluster Completeness Size vs Quantity. — F- — :

$$

$$BCF = \frac{2 \cdot BCP \cdot BCR}{BCP + BCR}$$

3.

, . , .

, , . $$$D=\{a,b,c,d,e,f,g,h,i\}$ , $$$t_1 = \{a,b,c,d,e\}$ $$$t_2=\{f,g,h,i\}$ («» «» ).

: $$$c_1 = \{a,b,c,d,g\}$, $$$c_2=\{e,f,h,i\}$.

3.1. BCubed

BCubed- :

$$

$$BCP(t_i)=\frac{1}{|t_i|} \sum_{d \in t_i}{BCP(d)}$$

$$

$$BCR(t_i)=\frac{1}{|t_i|} \sum_{d \in t_i}{BCR(d)}$$

:

$$

$$BCP(a)=BCP(b)=BCP(c)=BCP(d)=\frac{|t_1 \cap c_1|}{|c_1|}=0.8, BCP(e)=\frac{|t_1 \cap c_2|}{|c_2|}=0.25$$

$$

$$BCP(f)=BCP(h)=BCP(i)=\frac{|t_2 \cap c_2|}{|c_2|}=0.75, BCP(g)=\frac{|t_2 \cap c_1|}{|c_1|}=0.2$$

:

$$

$$BCP(t_1)=\frac{BCP(a)+BCP(b)+BCP(c)+BCP(d)+BCP(e)}{5}=\frac{4\cdot 0.8 + 0.25}{5}=0.69$$

$$

$$BCP(t_2)=\frac{BCP(f)+BCP(g)+BCP(h)+BCP(i)}{4}=\frac{3\cdot 0.75 + 0.2}{4}=0.6125$$

:

$$

$$BCR(a)=BCR(b)=BCR(c)=BCR(d)=\frac{|t_1 \cap c_1|}{|t_1|}=0.8, BCR(e)=\frac{|t_1 \cap c_2|}{|t_1|}=0.2$$

$$

$$BCR(f)=BCR(h)=BCR(i)=\frac{|t_2 \cap c_2|}{|t_2|}=0.75, BCP(g)=\frac{|t_2 \cap c_1|}{|t_2|}=0.25$$

$$

$$BCR(t_1)=\frac{BCR(a)+BCR(b)+BCR(c)+BCR(d)+BCR(e)}{5}=\frac{4\cdot 0.8 + 0.2}{5}=0.68$$

$$

$$BCR(t_2)=\frac{BCR(f)+BCR(g)+BCR(h)+BCR(i)}{4}=\frac{3\cdot 0.75 + 0.25}{4}=0.625$$

BCP BCR :

$$

$$BCP=\frac{BCP(t_1) + BCP(t_2)}{2}=0.65125$$

$$

$$BCR=\frac{BCR(t_1) + BCR(t_2)}{2}=0.6525$$

.

3.2. Expected Cluster Completeness

. , , , , - .

— F- — . , ? .

, , «». . — . : , , .

— :

$$

$$f:C \rightarrow T$$

$$$f$ (cluster completeness):

$$

$${CC}_f(t) = \max_{c \in f^{-1}(t)}{\frac{|c \cap t|}{|t|}}$$

:

$$

$${CC}_f(T) = \frac{1}{T} \sum_{t \in T} {CC}_f(t)$$

— , $$$f$. : .

. , $$$f(c)=t$,

$$

$$P\Big(f(c)=t\Big) = P(c, t) = \frac{|c \cap t|}{|c|}$$

$$$f$ :

$$

$$P(f) = \prod_{c \in C}{\frac{|c \cap f(c)|}{|c|}}$$

:

$$

$$ECC(t) = \sum_{f: C \rightarrow T}{P(f) \cdot CC_f(t)}$$

:

$$

$$ECC = \frac{1}{|T|} \sum_{t \in T}{ECC(t)}$$

:

$$

$$ECC = \sum_{f: C \rightarrow T}{P(f) \cdot {CC}_f(T)}$$

. $$$t$ $$$c_1$, $$$c_2$, ..., $$$c_k$, :

$$

$$|t \cap c_1| \ge |t \cap c_2| \ge ... \ge |t \cap c_k|$$

$$$c_1$ $$$t$

$$

$$P\Big(f(c_1) = t\Big) = \frac{|c_1 \cap t|}{|c_1|}$$

$$

$$R(c_1, t) = \frac{ | c_1 \cap t | }{| t |}$$

, , . $$$R(c_1, t)$.

$$$c_1$ , $$$p(c_2, t)$ $$$t$ $$$c_2$. $$$R(c_2, t)$. , ,

$$

$$P(c_1, t) \cdot R(c_1, t) + P(c_2, t) \cdot R (c_2, t) \cdot \Big(1 - P(c_1,t)\Big) + ...$$

ECC . sortedMatchings , , . Precision() Recall() . :

double ExpectedClusterCompleteness(const TMatchings& sortedMatchings) {
    double expectedClusterCompleteness = 0.;
    double probability = 1.;
    for (const TMatching& matching : sortedMatchings) {
        expectedClusterCompleteness += matching.Recall() * matching.Precision() * probability;
        probability *= 1. - matching.Precision();
    }
    return expectedClusterCompleteness;
}

, $$$F_1$-, !

ECC , 3. $$$t_1$ $$$c_1$, $$$t_2$ — $$$c_2$. :

$$$ECC(t_1) = R(c_1, t_2) \cdot P(c_1, t_1) + R(c_2, t_1) \cdot P(c_2, t_1) \cdot \Big(1 - P(c_1, t_1)\Big)$
$$$ECC(t_1) = {0.8}^2 + 0.2 \cdot 0.25 \cdot (1 - 0.8) = 0.65$

$$$ECC(t_2) = R(c_2, t_2) \cdot P(c_2, t_2) + R(c_1, t_2) \cdot P(c_1, t_2) \cdot \Big(1 - P(c_2, t_2)\Big)$
$$$ECC(t_2) = {0.75}^2 + 0.25 \cdot 0.2 \cdot (1 - 0.75) = 0.575$

, :

$$

$$ECC = \frac{ECC(t_1) + ECC(t_2)}{2} = 0.6125$$

4.

, 3, C++ MIT GitHub. Linux, Windows.

:

git clone https://github.com/yandex/cluster_metrics/ .
cmake .
cmake --build .

, 3. !

./cluster_metrics samples/sample_markup.tsv samples/sample_clusters.tsv
ECC   0.61250 (0.61250)
BCP   0.65125 (0.65125)
BCR   0.65250 (0.65250)
BCF1  0.65187 (0.65187)

«» , , . , , . , , . — .

5. ,

, , , .

. , , . , , :

: , . , , . , , , — . — ECC!

, , — . .

, , , . .

, , , ECC! ECC - , , , 100% . .

, 1 . : — .

^{_{Cluster Completeness}}

, , . , Cluster Homogeneity, Cluster Completeness, Rag Bag , Size vs Quantity .

, : , , , .

, 3, , .

, , : . , , .