Untuk mengantisipasi dimulainya kursus "Algoritma untuk Pengembang" telah mempersiapkan untuk Anda terjemahan dari materi lain yang bermanfaat.
Huffman coding adalah algoritma kompresi data yang merumuskan ide dasar kompresi file. Pada artikel ini, kita akan berbicara tentang pengkodean panjang tetap dan variabel, kode yang diterjemahkan secara unik, aturan awalan, dan pembangunan pohon Huffman.Kita tahu bahwa setiap karakter disimpan sebagai urutan 0 dan 1 dan membutuhkan 8 bit. Ini disebut pengkodean panjang tetap karena setiap karakter menggunakan jumlah bit tetap yang sama untuk menyimpan.Katakanlah teks diberikan. Bagaimana kita bisa mengurangi jumlah ruang yang dibutuhkan untuk menyimpan satu karakter?Ide dasarnya adalah pengkodean panjang variabel. Kita dapat menggunakan fakta bahwa beberapa karakter dalam teks lebih umum daripada yang lain ( lihat di sini ) untuk mengembangkan algoritma yang akan mewakili urutan karakter yang sama dengan bit yang lebih sedikit. Saat mengkode panjang variabel, kami menetapkan sejumlah variabel bit untuk karakter tergantung pada frekuensi kemunculannya dalam teks ini. Pada akhirnya, beberapa karakter dapat memakan waktu hanya 1 bit, dan yang lain 2 bit, 3 atau lebih. Masalah dengan pengkodean panjang variabel hanya decoding urutan berikutnya.Bagaimana, mengetahui urutan bit, mendekodekannya secara unik?Pertimbangkan string "aabacdab" . Ini memiliki 8 karakter, dan ketika menyandikan panjang tetap, 64 bit akan diperlukan untuk menyimpannya. Perhatikan bahwa frekuensi karakter "a", "b", "c" dan "d" masing-masing adalah 4, 2, 1, 1. Mari kita coba bayangkan "aabacdab" dengan bit lebih sedikit, menggunakan fakta bahwa "a" lebih umum daripada "b" dan "b" lebih umum daripada "c" dan "d" . Untuk memulainya, kita menyandikan "a" menggunakan satu bit sama dengan 0, "b" kita menetapkan kode dua-bit 11, dan menggunakan tiga bit 100 dan 011 kita menyandikan "c" dan"D" .Sebagai hasilnya, kami akan berhasil:Jadi, kami menyandikan string "aabacdab" sebagai 00110100011011 (0 | 0 | 11 | 0 | 100 | 011 | 0 | 11) menggunakan kode yang disajikan di atas. Namun, masalah utamanya adalah decoding. Ketika kami mencoba untuk memecahkan kode garis 00110100011011 , kami mendapatkan hasil yang ambigu, karena dapat direpresentasikan sebagai:0|011|0|100|011|0|11 adacdab
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
...dll.Untuk menghindari ambiguitas ini, kita harus memastikan bahwa pengkodean kita memenuhi konsep seperti aturan awalan , yang pada gilirannya menyiratkan bahwa kode dapat diterjemahkan hanya dalam satu cara yang unik. Aturan awalan memastikan bahwa tidak ada kode yang merupakan awalan dari yang lain. Menurut kode, maksud kami bit yang digunakan untuk mewakili karakter tertentu. Dalam contoh di atas, 0 adalah awalan 011 , yang melanggar aturan awalan. Jadi, jika kode kita memenuhi aturan awalan, maka kita dapat mendekode secara unik (dan sebaliknya).Mari kita tinjau contoh di atas. Kali ini kami akan menetapkan karakter "a", "b", "c" dan "d" Kode yang memenuhi aturan awalan.Menggunakan pengkodean ini, string "aabacdab" akan dikodekan sebagai 00100100011010 (0 | 0 | 10 | 0 | 100 | 011 | 0 | 10) . Dan di sini 00100100011010 kita dapat secara unik mendekode dan kembali ke baris asli kita "aabacdab" .Coding Huffman
Sekarang kami telah menemukan pengkodean panjang variabel dan aturan awalan, mari kita bicara tentang pengkodean Huffman.Metode ini didasarkan pada penciptaan pohon biner. Di dalamnya, sebuah simpul dapat berupa terbatas atau internal. Awalnya, semua simpul dianggap daun (daun), yang mewakili simbol itu sendiri dan beratnya (yaitu, frekuensi kejadian). Node internal berisi bobot karakter dan merujuk ke dua node turunan. Secara umum, bit "0" mewakili tindak di cabang kiri, dan "1" mewakili di sebelah kanan. Dalam pohon lengkap ada N daun dan N-1 node internal. Disarankan bahwa ketika membangun pohon Huffman, karakter yang tidak digunakan dibuang untuk mendapatkan kode dengan panjang optimal.Kami akan menggunakan antrian prioritas untuk membangun pohon Huffman, di mana simpul dengan frekuensi terendah akan diberi prioritas tertinggi. Langkah-langkah konstruksi dijelaskan di bawah ini:- Buat simpul daun untuk setiap karakter dan tambahkan ke antrian prioritas.
- Sementara dalam antrean lebih dari satu lembar, lakukan hal berikut:
- Hapus dua node dengan prioritas tertinggi (dengan frekuensi terendah) dari antrian;
- Buat simpul internal baru di mana dua node ini akan menjadi ahli waris, dan frekuensi kemunculannya akan sama dengan jumlah frekuensi dua node ini.
- Tambahkan node baru ke antrian prioritas.
- Satu-satunya simpul yang tersisa adalah root, ini akan menyelesaikan konstruksi pohon.
Bayangkan kita memiliki beberapa teks yang hanya terdiri dari karakter "a," "b," "c," "d," dan "e," dan frekuensinya masing-masing adalah 15, 7, 6, 6, dan 5. Di bawah ini adalah ilustrasi yang mencerminkan langkah-langkah algoritma.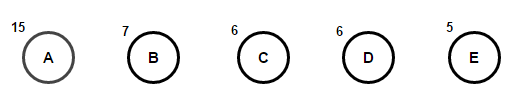
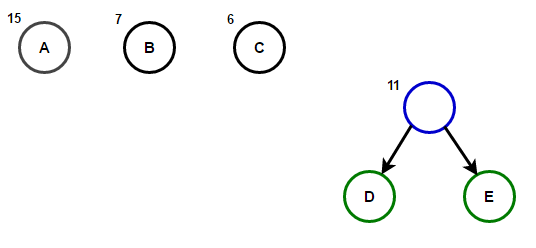
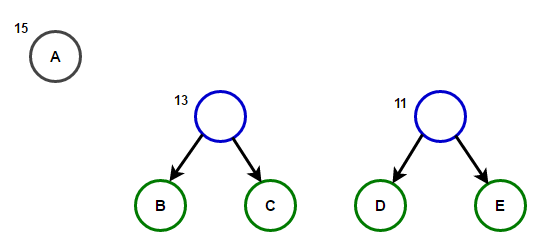
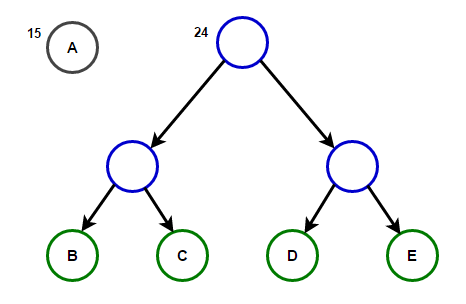
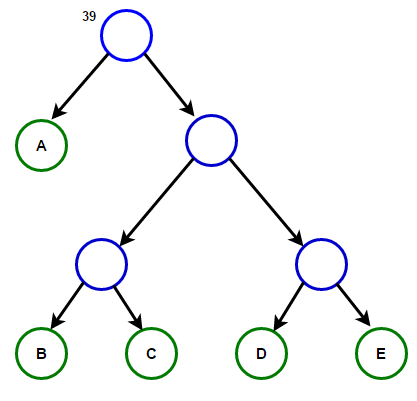 Path dari root ke sembarang simpul akan menyimpan kode awalan yang optimal (juga dikenal sebagai kode Huffman) yang sesuai dengan karakter yang terkait dengan simpul akhir itu.
Path dari root ke sembarang simpul akan menyimpan kode awalan yang optimal (juga dikenal sebagai kode Huffman) yang sesuai dengan karakter yang terkait dengan simpul akhir itu.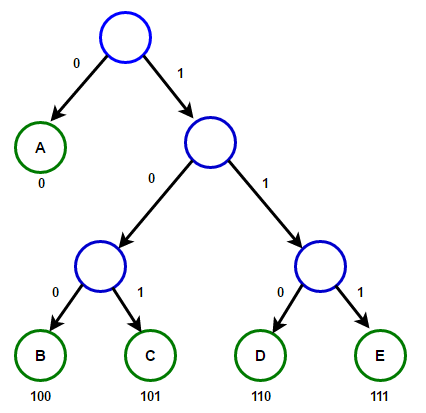 Huffman TreeDi bawah ini Anda akan menemukan implementasi algoritma kompresi Huffman di C ++ dan Java:
Huffman TreeDi bawah ini Anda akan menemukan implementasi algoritma kompresi Huffman di C ++ dan Java:#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
struct Node
{
char ch;
int freq;
Node *left, *right;
};
Node* getNode(char ch, int freq, Node* left, Node* right)
{
Node* node = new Node();
node->ch = ch;
node->freq = freq;
node->left = left;
node->right = right;
return node;
}
struct comp
{
bool operator()(Node* l, Node* r)
{
return l->freq > r->freq;
}
};
void encode(Node* root, string str,
unordered_map<char, string> &huffmanCode)
{
if (root == nullptr)
return;
if (!root->left && !root->right) {
huffmanCode[root->ch] = str;
}
encode(root->left, str + "0", huffmanCode);
encode(root->right, str + "1", huffmanCode);
}
void decode(Node* root, int &index, string str)
{
if (root == nullptr) {
return;
}
if (!root->left && !root->right)
{
cout << root->ch;
return;
}
index++;
if (str[index] =='0')
decode(root->left, index, str);
else
decode(root->right, index, str);
}
void buildHuffmanTree(string text)
{
unordered_map<char, int> freq;
for (char ch: text) {
freq[ch]++;
}
priority_queue<Node*, vector<Node*>, comp> pq;
for (auto pair: freq) {
pq.push(getNode(pair.first, pair.second, nullptr, nullptr));
}
while (pq.size() != 1)
{
Node *left = pq.top(); pq.pop();
Node *right = pq.top(); pq.pop();
int sum = left->freq + right->freq;
pq.push(getNode('\0', sum, left, right));
}
Node* root = pq.top();
unordered_map<char, string> huffmanCode;
encode(root, "", huffmanCode);
cout << "Huffman Codes are :\n" << '\n';
for (auto pair: huffmanCode) {
cout << pair.first << " " << pair.second << '\n';
}
cout << "\nOriginal string was :\n" << text << '\n';
string str = "";
for (char ch: text) {
str += huffmanCode[ch];
}
cout << "\nEncoded string is :\n" << str << '\n';
int index = -1;
cout << "\nDecoded string is: \n";
while (index < (int)str.size() - 2) {
decode(root, index, str);
}
}
int main()
{
string text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
return 0;
}
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class Node
{
char ch;
int freq;
Node left = null, right = null;
Node(char ch, int freq)
{
this.ch = ch;
this.freq = freq;
}
public Node(char ch, int freq, Node left, Node right) {
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
};
class Huffman
{
public static void encode(Node root, String str,
Map<Character, String> huffmanCode)
{
if (root == null)
return;
if (root.left == null && root.right == null) {
huffmanCode.put(root.ch, str);
}
encode(root.left, str + "0", huffmanCode);
encode(root.right, str + "1", huffmanCode);
}
public static int decode(Node root, int index, StringBuilder sb)
{
if (root == null)
return index;
if (root.left == null && root.right == null)
{
System.out.print(root.ch);
return index;
}
index++;
if (sb.charAt(index) == '0')
index = decode(root.left, index, sb);
else
index = decode(root.right, index, sb);
return index;
}
public static void buildHuffmanTree(String text)
{
Map<Character, Integer> freq = new HashMap<>();
for (int i = 0 ; i < text.length(); i++) {
if (!freq.containsKey(text.charAt(i))) {
freq.put(text.charAt(i), 0);
}
freq.put(text.charAt(i), freq.get(text.charAt(i)) + 1);
}
PriorityQueue<Node> pq = new PriorityQueue<>(
(l, r) -> l.freq - r.freq);
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
pq.add(new Node(entry.getKey(), entry.getValue()));
}
while (pq.size() != 1)
{
Node left = pq.poll();
Node right = pq.poll();
int sum = left.freq + right.freq;
pq.add(new Node('\0', sum, left, right));
}
Node root = pq.peek();
Map<Character, String> huffmanCode = new HashMap<>();
encode(root, "", huffmanCode);
System.out.println("Huffman Codes are :\n");
for (Map.Entry<Character, String> entry : huffmanCode.entrySet()) {
System.out.println(entry.getKey() + " " + entry.getValue());
}
System.out.println("\nOriginal string was :\n" + text);
StringBuilder sb = new StringBuilder();
for (int i = 0 ; i < text.length(); i++) {
sb.append(huffmanCode.get(text.charAt(i)));
}
System.out.println("\nEncoded string is :\n" + sb);
int index = -1;
System.out.println("\nDecoded string is: \n");
while (index < sb.length() - 2) {
index = decode(root, index, sb);
}
}
public static void main(String[] args)
{
String text = "Huffman coding is a data compression algorithm.";
buildHuffmanTree(text);
}
}
Catatan: memori yang digunakan oleh string input adalah 47 * 8 = 376 bit, dan string yang disandikan hanya membutuhkan 194 bit, mis. data dikompresi sekitar 48%. Dalam program C ++ di atas, kami menggunakan kelas string untuk menyimpan string yang disandikan agar program dapat dibaca.Karena struktur data yang efektif dari antrian prioritas memerlukan O (log (N)) waktu untuk dimasukkan, dan dalam pohon biner lengkap dengan daun N ada 2N-1 node, dan pohon Huffman adalah pohon biner lengkap, algoritma bekerja untuk O (Nlog (Nlog) )) waktu, di mana N adalah jumlah karakter.Sumber:
en.wikipedia.org/wiki/Huffman_codingen.wikipedia.org/wiki/Variable-length_codewww.youtube.com/watch?v=5wRPin4oxCo
.