Halo, Habr!Kami mengingatkan Anda bahwa sebelumnya kami mengumumkan buku " Pembelajaran Mesin Tanpa Kata-Kata Tambahan " - dan sekarang sudah dijual . Terlepas dari kenyataan bahwa bagi pemula di MO, buku itu memang bisa menjadi desktop , beberapa topik di dalamnya masih belum tersentuh. Oleh karena itu, kami menawarkan kepada semua orang yang tertarik untuk menerjemahkan sebuah artikel oleh Simon Kerstens tentang esensi algoritma MCMC dengan implementasi algoritma semacam itu di Python.Metode Monte Carlo untuk rantai Markov (MCMC) adalah kelas metode yang kuat untuk pengambilan sampel dari distribusi probabilitas yang hanya diketahui hingga konstanta normalisasi tertentu (tidak diketahui).Namun, sebelum mempelajari MCMC, mari kita bahas mengapa Anda mungkin perlu membuat pilihan seperti itu. Jawabannya adalah: Anda mungkin tertarik pada sampel itu sendiri dari sampel (misalnya, untuk menentukan parameter yang tidak diketahui menggunakan metode derivasi Bayesian), atau untuk memperkirakan nilai yang diharapkan dari fungsi relatif terhadap distribusi probabilitas (misalnya, untuk menghitung jumlah termodinamika dari distribusi keadaan dalam fisika statistik). Terkadang kami hanya tertarik pada mode distribusi probabilitas. Dalam hal ini, kami mendapatkannya dengan metode optimasi numerik, sehingga tidak perlu membuat pilihan lengkap.Ternyata pengambilan sampel dari distribusi probabilitas apa pun kecuali yang paling primitif adalah tugas yang sulit. Metode transformasi terbalik adalah teknik dasar untuk pengambilan sampel dari distribusi probabilitas, yang, bagaimanapun, membutuhkan penggunaan fungsi distribusi kumulatif, dan untuk menggunakannya, pada gilirannya, Anda perlu mengetahui konstanta normalisasi, yang biasanya tidak diketahui. Pada prinsipnya, konstanta normalisasi dapat diperoleh dengan integrasi numerik, tetapi metode ini dengan cepat menjadi tidak praktis dengan peningkatan jumlah dimensi. Pengambilan Sampel DeviasiItu tidak memerlukan distribusi yang dinormalisasi, tetapi untuk mengimplementasikannya secara efektif, perlu banyak tahu tentang distribusi yang menarik bagi kita. Selain itu, metode ini sangat menderita dari kutukan dimensi - ini berarti efektivitasnya menurun dengan cepat dengan peningkatan jumlah variabel. Itulah mengapa Anda perlu mengatur penerimaan sampel representatif secara cerdas dari distribusi Anda - tidak perlu mengetahui konstanta normalisasi.Algoritma MCMC adalah kelas metode yang dirancang khusus untuk ini. Mereka kembali ke artikel tengara Metropolis dan lainnya ; Metropolis mengembangkan algoritma MCMC pertama yang dinamai menurut namanyadan dirancang untuk menghitung keadaan keseimbangan sistem dua dimensi bidang keras. Bahkan, para peneliti sedang mencari metode universal yang akan memungkinkan kita untuk menghitung nilai-nilai yang diharapkan ditemukan dalam fisika statistik.Artikel ini akan membahas dasar-dasar pengambilan sampel MCMC.RANTAI MARKOVSekarang kita mengerti mengapa kita perlu mengambil sampel, mari kita beralih ke jantung MCMC: rantai Markov. Apa itu rantai Markov? Tanpa membahas perincian teknis, kita dapat mengatakan bahwa rantai Markov adalah urutan acak negara dalam ruang keadaan tertentu, di mana probabilitas memilih negara tertentu hanya bergantung pada keadaan rantai saat ini, tetapi tidak pada sejarah sebelumnya: rantai ini tidak memiliki memori. Dalam kondisi tertentu, rantai Markov memiliki distribusi stasioner unik negara, yang konvergen, mengatasi sejumlah negara. Setelah sejumlah negara bagian dalam rantai Markov, distribusi invarian diperoleh.Untuk mengambil sampel dari distribusi, 
algoritma MCMC membuat dan mensimulasikan rantai Markov yang distribusi stasionernya; ini berarti bahwa setelah periode "benih" awal, keadaan rantai Markov tersebut didistribusikan sesuai dengan prinsip . Karena itu, kita hanya perlu menyelamatkan negara untuk mendapatkan sampel .Untuk tujuan pendidikan, marilah kita mempertimbangkan ruang keadaan diskrit dan "waktu" diskrit. Kuantitas kunci yang mencirikan rantai Markov adalah operator transisi yang 
menunjukkan kemungkinan berada dalam keadaan 
pada suatu waktu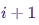 
, asalkan rantai tersebut berada dalam keadaan 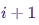pada suatu waktu i.Sekarang hanya untuk bersenang-senang (dan sebagai demonstrasi), mari kita cepat-cepat menenun rantai Markov dengan distribusi stasioner yang unik. Mari kita mulai dengan beberapa impor dan pengaturan untuk grafik:%matplotlib notebook
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 6]
np.random.seed(42)
Rantai Markov akan mengelilingi ruang keadaan diskrit yang dibentuk oleh tiga kondisi cuaca:state_space = ("sunny", "cloudy", "rainy")
Dalam ruang keadaan diskrit, operator transisi hanyalah sebuah matriks. Dalam kasus kami, kolom dan baris sesuai dengan cuaca cerah, berawan, dan hujan. Mari kita pilih nilai yang relatif masuk akal untuk probabilitas semua transisi:transition_matrix = np.array(((0.6, 0.3, 0.1),
(0.3, 0.4, 0.3),
(0.2, 0.3, 0.5)))
Baris menunjukkan status di mana sirkuit saat ini dapat ditemukan, dan kolom menunjukkan status di mana sirkuit dapat pergi. Jika kita mengambil langkah "waktu" dari rantai Markov dalam satu jam, maka, asalkan cuaca cerah sekarang, ada kemungkinan 60% bahwa cuaca cerah akan berlanjut selama satu jam berikutnya. Ada juga kemungkinan 30% bahwa akan ada cuaca berawan di jam berikutnya, dan 10% kemungkinan itu akan turun hujan segera setelah cuaca cerah. Ini juga berarti bahwa nilai di setiap baris bertambah menjadi satu.Mari kita sedikit menggerakkan rantai Markov kami:n_steps = 20000
states = [0]
for i in range(n_steps):
states.append(np.random.choice((0, 1, 2), p=transition_matrix[states[-1]]))
states = np.array(states)
Kita dapat mengamati bagaimana rantai Markov menyatu dengan distribusi stasioner, menghitung probabilitas empiris dari masing-masing negara sebagai fungsi dari panjang rantai:def despine(ax, spines=('top', 'left', 'right')):
for spine in spines:
ax.spines[spine].set_visible(False)
fig, ax = plt.subplots()
width = 1000
offsets = range(1, n_steps, 5)
for i, label in enumerate(state_space):
ax.plot(offsets, [np.sum(states[:offset] == i) / offset
for offset in offsets], label=label)
ax.set_xlabel("number of steps")
ax.set_ylabel("likelihood")
ax.legend(frameon=False)
despine(ax, ('top', 'right'))
plt.show()
HONOR OF ALL MCMC: ALGORITMA METROPOLIS-HASTINGTentu saja, semua ini sangat menarik, tetapi kembali ke proses pengambilan sampel dari distribusi probabilitas yang berubah-ubah 
. Ini bisa berupa diskrit, dalam hal ini kita akan terus berbicara tentang matriks transisi 
, atau kontinu, dalam hal ini akan menjadi inti transisi. Selanjutnya, kami akan berbicara tentang distribusi berkelanjutan, tetapi semua konsep yang kami pertimbangkan di sini juga berlaku untuk kasus-kasus terpisah.Jika kita dapat merancang inti transisi sedemikian rupa sehingga negara bagian berikutnya sudah dideduksi , maka ini dapat dibatasi, karena rantai Markov kita ... akan langsung diambil sampelnya . Sayangnya, untuk mencapai ini, kita perlu kemampuan untuk mengambil sampelapa yang tidak bisa kita lakukan - jika tidak, Anda tidak akan membacanya, kan?Solusinya adalah memecah inti transisi 
menjadi dua bagian: langkah proposal dan langkah penerimaan / penolakan. Distribusi tambahan muncul pada langkah sampel
dari mana keadaan rantai berikutnya yang mungkin dipilih. Kita tidak hanya dapat membuat pilihan dari distribusi ini, tetapi kita dapat secara sewenang-wenang memilih distribusi itu sendiri. Namun, ketika mendesain, seseorang harus berusaha untuk datang ke konfigurasi seperti itu di mana sampel yang diambil dari distribusi ini akan berkorelasi minimal dengan keadaan saat ini dan pada saat yang sama memiliki peluang bagus untuk melewati fase penerimaan. Langkah menerima / membuang di atas adalah bagian kedua dari inti transisi; pada tahap ini, kesalahan yang terkandung dalam status percobaan dipilih dari dikoreksi 
. Di sini, probabilitas penerimaan yang berhasil dihitung 
dan sampel diambil dengan probabilitas seperti keadaan berikutnya dalam rantai. Mendapatkan status selanjutnya darikemudian dilakukan sebagai berikut: pertama, pengadilan diambil dari . Kemudian diambil sebagai keadaan berikutnya dengan probabilitas atau dibuang dengan probabilitas 
, dan dalam kasus terakhir, keadaan saat ini disalin dan digunakan sebagai yang berikutnya.Akibatnya, kita memiliki
kondisi yang cukup untuk rantai Markov memiliki sebagai distribusi stasioner adalah sebagai berikut: Inti transisi harus menyerahkan keseimbangan rinci atau sebagai menulis dalam literatur fisik, reversibilitas mikroskopis :
.Ini berarti kemungkinan berada dalam keadaan 
dan bergerak dari sana ke sana
harus sama dengan probabilitas proses kebalikannya, yaitu, mampu dan masuk ke keadaan . Kernel transisi dari sebagian besar algoritma MCMC memenuhi kondisi ini.Agar inti transisi dua bagian untuk mematuhi keseimbangan terperinci, perlu untuk memilih dengan benar 
, yaitu, untuk memastikan bahwa memungkinkan Anda untuk memperbaiki segala asimetri dalam aliran probabilitas dari / ke atau . Metropolis-Hastings algoritma menggunakan kriteria diterimanya Metropolis:
.Dan di sini keajaiban dimulai: kita hanya tahu konstanta, tetapi itu tidak masalah, karena konstanta yang tidak diketahui ini membatalkan ekspresi untuk! Properti paccpacc inilah yang memastikan pengoperasian algoritma berdasarkan pada algoritma Metropolis-Hastings pada distribusi yang tidak dinormalisasi. Distribusi pembantu simetris c sering digunakan 
, dalam hal ini algoritma Metropolis-Hastings direduksi menjadi algoritma Metropolis asli (kurang umum) yang dikembangkan pada tahun 1953. Dalam algoritma asli
.Dalam hal ini, inti transisi lengkap dari Metropolis-Hastings dapat ditulis sebagai
.KAMI MELAKSANAKAN ALGORITMA METROPOLIS-HASTING DI PYTHONNah, sekarang kita telah menemukan cara kerja algoritma Metropolis-Hastings, mari beralih ke implementasinya. Pertama, kita menetapkan probabilitas logaritmik dari distribusi dari mana kita akan membuat pilihan - tanpa konstanta normalisasi; diasumsikan bahwa kita tidak mengenal mereka. Selanjutnya, kami bekerja dengan distribusi normal standar:def log_prob(x):
return -0.5 * np.sum(x ** 2)
Selanjutnya, kami memilih distribusi bantu simetris. Secara umum, kinerja algoritma Metropolis-Hastings dapat ditingkatkan jika Anda menyertakan informasi yang sudah Anda ketahui tentang distribusi dari mana Anda ingin membuat pilihan dalam distribusi tambahan. Pendekatan yang disederhanakan terlihat seperti ini: kami mengambil keadaan saat ini xdan memilih sampel dari , yaitu, menetapkan ukuran langkah tertentu Δdan ke kiri atau kanan dari keadaan kami saat ini tidak lebih dari 
:def proposal(x, stepsize):
return np.random.uniform(low=x - 0.5 * stepsize,
high=x + 0.5 * stepsize,
size=x.shape)
Akhirnya, kami menghitung probabilitas bahwa proposal akan diterima:def p_acc_MH(x_new, x_old, log_prob):
return min(1, np.exp(log_prob(x_new) - log_prob(x_old)))
Sekarang kami menyatukan semua ini ke dalam implementasi yang benar-benar singkat dari tahap pengambilan sampel untuk algoritma Metropolis-Hastings:def sample_MH(x_old, log_prob, stepsize):
x_new = proposal(x_old, stepsize)
accept = np.random.random() < p_acc(x_new, x_old, log_prob)
if accept:
return accept, x_new
else:
return accept, x_old
Selain keadaan berikutnya dalam rantai Markov, x_newatau x_old, kami juga mengembalikan informasi tentang apakah langkah MCMC diadopsi. Ini akan memungkinkan kami untuk melacak dinamika pengumpulan sampel. Sebagai kesimpulan dari implementasi ini, kami menulis sebuah fungsi yang akan dipanggil berulang sample_MHdan dengan demikian membangun rantai Markov:def build_MH_chain(init, stepsize, n_total, log_prob):
n_accepted = 0
chain = [init]
for _ in range(n_total):
accept, state = sample_MH(chain[-1], log_prob, stepsize)
chain.append(state)
n_accepted += accept
acceptance_rate = n_accepted / float(n_total)
return chain, acceptance_rate
MENGUJI ALGORITMA METROPOLIS-HAST KAMI DAN PENELITIAN PERILAKUNYAMungkin, sekarang Anda tidak sabar untuk melihat semua ini beraksi. Kami akan melakukan ini, kami akan membuat keputusan berdasarkan argumen stepsizedan n_total:chain, acceptance_rate = build_MH_chain(np.array([2.0]), 3.0, 10000, log_prob)
chain = [state for state, in chain]
print("Acceptance rate: {:.3f}".format(acceptance_rate))
last_states = ", ".join("{:.5f}".format(state)
for state in chain[-10:])
print("Last ten states of chain: " + last_states)
Acceptance rate: 0.722
Last ten states of chain: -0.84962, -0.84962, -0.84962, -0.08692, 0.92728, -0.46215, 0.08655, -0.33841, -0.33841, -0.33841
Semuanya baik-baik saja. Jadi, apakah itu berhasil? Kami berhasil mengambil sampel di sekitar 71% kasus, dan kami memiliki rantai negara. Beberapa negara bagian pertama di mana rantai belum konvergen ke distribusi stasionernya harus dibuang. Mari kita periksa apakah kondisi yang kita pilih benar-benar memiliki distribusi normal:def plot_samples(chain, log_prob, ax, orientation='vertical', normalize=True,
xlims=(-5, 5), legend=True):
from scipy.integrate import quad
ax.hist(chain, bins=50, density=True, label="MCMC samples",
orientation=orientation)
if normalize:
Z, _ = quad(lambda x: np.exp(log_prob(x)), -np.inf, np.inf)
else:
Z = 1.0
xses = np.linspace(xlims[0], xlims[1], 1000)
yses = [np.exp(log_prob(x)) / Z for x in xses]
if orientation == 'horizontal':
(yses, xses) = (xses, yses)
ax.plot(xses, yses, label="true distribution")
if legend:
ax.legend(frameon=False)
fig, ax = plt.subplots()
plot_samples(chain[500:], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
Tampak hebat!Bagaimana dengan parameter stepsizedan n_total? Kami pertama-tama membahas ukuran langkah: menentukan seberapa jauh status percobaan dapat dihapus dari kondisi rangkaian saat ini. Oleh karena itu, ini adalah parameter distribusi tambahan qyang mengontrol seberapa besar langkah acak yang diambil oleh rantai Markov. Jika ukuran langkah terlalu besar, status percobaan sering berakhir di bagian akhir distribusi, di mana nilai probabilitasnya rendah. Mekanisme pengambilan sampel Metropolis-Hastings membuang sebagian besar langkah-langkah ini, akibatnya tingkat penerimaan dikurangi dan konvergensi melambat secara signifikan. Lihat diri mu sendiri:def sample_and_display(init_state, stepsize, n_total, n_burnin, log_prob):
chain, acceptance_rate = build_MH_chain(init_state, stepsize, n_total, log_prob)
print("Acceptance rate: {:.3f}".format(acceptance_rate))
fig, ax = plt.subplots()
plot_samples([state for state, in chain[n_burnin:]], log_prob, ax)
despine(ax)
ax.set_yticks(())
plt.show()
sample_and_display(np.array([2.0]), 30, 10000, 500, log_prob)
Acceptance rate: 0.116
Tidak terlalu keren, bukan? Sekarang tampaknya yang terbaik adalah mengatur ukuran langkah kecil. Ternyata ini juga bukan keputusan yang cerdas, karena rantai Markov akan menyelidiki distribusi probabilitas dengan sangat lambat, dan karena itu juga tidak akan menyatu secepat dengan ukuran langkah yang dipilih dengan baik:sample_and_display(np.array([2.0]), 0.1, 10000, 500, log_prob)
Acceptance rate: 0.992
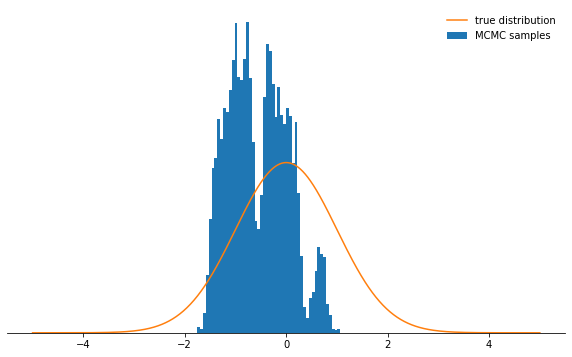Terlepas dari bagaimana Anda memilih parameter ukuran langkah, rantai Markov akhirnya menyatu ke distribusi stasioner. Tetapi ini mungkin membutuhkan banyak waktu. Waktu di mana kita akan mensimulasikan rantai Markov n_totalditentukan oleh parameter - ini hanya menentukan berapa banyak status rantai Markov (dan, oleh karena itu, sampel yang dipilih) yang akhirnya akan kita miliki. Jika rantai konvergen lambat, maka perlu ditingkatkan n_totalagar rantai Markov punya waktu untuk "melupakan" keadaan awal. Oleh karena itu, kami akan meninggalkan ukuran langkah kecil dan meningkatkan jumlah sampel dengan meningkatkan parameter n_total:sample_and_display(np.array([2.0]), 0.1, 500000, 25000, log_prob)
Acceptance rate: 0.990
Mungkin kita sedang bergerak menuju tujuan ...KESIMPULANMempertimbangkan semua hal di atas, saya harap sekarang Anda secara intuitif memahami esensi dari algoritma Metropolis-Hastings, parameternya, dan memahami mengapa ini adalah alat yang sangat berguna untuk memilih dari distribusi probabilitas non-standar yang mungkin Anda temui dalam praktik.Saya sangat menyarankan Anda bereksperimen dengan kode yang diberikan di sini.- sehingga Anda terbiasa dengan perilaku algoritma dalam berbagai keadaan dan memahaminya lebih dalam. Coba distribusi tambahan asimetris! Apa yang akan terjadi jika Anda tidak mengkonfigurasi kriteria penerimaan dengan benar? Apa yang terjadi jika Anda mencoba mengambil sampel dari distribusi bimodal? Bisakah Anda menemukan cara untuk secara otomatis menyesuaikan ukuran langkah? Apa jebakan di sini? Jawab sendiri pertanyaan-pertanyaan ini!