💇🏻 👋🏽 🤷🏿 Persamaan diferensial nonlinier, diskresi ruang-waktu dan produk epsilon 📫 👆🏻 ⚰️

Seluruh konten artikel ini merupakan konsekuensi dari penyelesaian masalah tingkat tahun pertama kursus institut dalam analisis matematika.

Di sini kami memperkenalkan produk baru untuk fungsi kisi (kami akan menyebutnya multiplikasi epsilon), yang memberi kami kesempatan untuk melihat hubungan yang menarik antara persamaan diferensial integral (termasuk yang nonlinear) dan hubungan perulangan. Ini memungkinkan Anda untuk melihat beberapa metode untuk menyelesaikannya dari sudut yang tidak biasa.

Tetapi, yang menurut saya sangat menarik, adalah bahwa karya baru itu juga memungkinkan kita untuk "bernalar" tentang hal-hal mendasar seperti kelangsungan ruang-waktu. Alasan ini, tentu saja, harus dianggap, sebagai latihan intelektual.

Tampak bagi saya bahwa ini matematika rebus atau, jika Anda suka, perjalanan matematika kecil di tingkat pengetahuan tahun pertama atau kedua dari universitas teknik mungkin menarik minat para pembaca Habr yang tertarik pada matematika.

Komentar

Anda tidak akan melihat tautan apa pun dan, secara umum, semua ini adalah hasil dari pemikiran satu orang
mungkin (dan bahkan kemungkinan besar), semua ini bukan hal baru, dan mungkin beberapa istilah yang saya gunakan tidak sesuai dengan tradisi matematika, tetapi karena ini bukan publikasi ilmiah, tidak ada klaim untuk hal baru dan semua ini cukup sederhana, maka ini perbedaan terminologis, menurut saya, bukanlah sesuatu yang sangat penting

Ringkasan

Pada artikel ini, kita akan berbicara tentang dua jenis fungsi (didefinisikan dalam bidang bilangan real): analitik dan kisi.

1

, $F(x), G(x), ...$ , ( $N_0$ ), $f_n, g_n, ...$ . $A^\epsilon$ .

2

, . , . ( ),

Kami akan membangun korespondensi satu-ke-satu antara fungsi dari dua kelas ini. Kami juga akan memperkenalkan operasi baru untuk fungsi kisi. Operasi ini akan mirip dengan operasi "normal" pada fungsi "normal". Kami akan membedakan operasi baru ini dengan menambahkan awalan "epsilon". Jadi turunan "biasa" akan sesuai dengan turunan epsilon , produk biasa dengan produk epsilon , integrasi biasa ke integrasi epsilon , dll. Selain itu, jika operasi tetap tidak berubah (seperti dalam kasus penjumlahan dan pengurangan), nama tidak akan berubah.

Salah satu tujuan utama dari memperkenalkan operasi ini adalah sederhana - untuk menjaga sifat-sifat produk turunan fungsi:

$(F(x)G(x))' = F'(x)G(x) + F(x)G'(x)$

Apa dalam kasus fungsi kisi (

$\in A^\epsilon$ ) akan terlihat seperti

$\overset{\displaystyle\epsilon}{\nabla} (f_n \overset{\displaystyle\epsilon}{*}g_n) = \overset{\displaystyle\epsilon}{\nabla} f_n \overset{\displaystyle\epsilon}{*}g_n + f_n \overset{\displaystyle\epsilon}{*}\overset{\displaystyle\epsilon}{\nabla} g_n$

dimana

$\overset{\displaystyle\epsilon}{\nabla}$ - operator turunan epsilon kiri

$\overset{\displaystyle\epsilon}{*}$ - epsilon-multiplikasi

Ini akan memungkinkan kita (dengan analogi, misalnya, dengan transformasi Laplace) untuk memperkenalkan transformasi baru, yang kita sebuttransformasi epsilon. Ini akan memberi kita kesempatan untuk mentransformasikan persamaan diferensial integral nonlinier dalam kasus umum menjadi ekspresi berulang dan menyelesaikannya (secara numerik atau analitik), masing-masing, dengan metode berulang.

. Keterangan

Kebalikannya juga benar: kita mendapatkan kesempatan untuk memecahkan hubungan rekurensi dengan metode persamaan diferensial terpisahkan

Fakta penting dalam kasus ini adalah ketika langkah fungsi kisi cenderung nol (

$\epsilon \to 0$ ), semua fungsi epsilon, operasi epsilon, dan persamaan perulangan kami cenderung ke fungsi "biasa" (analitik di sebelah kanan nol), operasi biasa di antara mereka, dan persamaan diferensial-integral biasa.

Tapi kemudian, ini mengarah ke pertanyaan mendasar: apakah epsilon-perkalian bukan perkalian “benar” di dunia fisik kita (setidaknya di mana ruang atau waktu terlibat)?

Jadi, misalnya, berbicara tentang waktu, dengan langkah yang cukup kecil (misalnya, tentang urutan waktu Planck

$t_p \sim 10^{-43}$ dtk) persamaan epsilon-Schrödinger c

$\epsilon\sim t_p$ untuk proses waktu dengan waktu karakteristik

$t \gg t_p$ (atau dalam domain frekuensi dengan frekuensi

$\omega \ll 1/\epsilon$ ) akan memberikan hasil yang sama dengan persamaan Schrödinger biasa, tetapi pada saat yang sama, kuantisasi waktu diperkenalkan secara alami.

Pada prinsipnya, argumen serupa mungkin untuk ruang.

Sebutan yang digunakan dalam artikel

$f_n, g_n, p_n ...$ — ,

$\{0,\epsilon,2\epsilon,\ldots\}$ ,

$\epsilon \in R$ ,

$\epsilon>0$ .

$f_n$ ( , ,

$g_n,p_n$ )

$n\epsilon$

$A^\epsilon$ —

$f_n$

$f$ — ,

$f_n$

$f$

$F(x), G(x), ..$ — «» . ( )

$\epsilon$ — :

$f_k = f(k\epsilon)$ .

$f_n$

$n\epsilon$

$\nabla$ — , :

$\nabla F(x) = F ^{'}(x)$

$\overset{\displaystyle\epsilon}{\nabla}$ — , - :

$\overset{\displaystyle\epsilon}{\nabla}{f_n} = f_n^\overset{\displaystyle\epsilon}{'}$

$\nabla_F$ — , , ,

$F(x)$ (

$F(x)$ ) , ,

$\nabla_F(F(x)G(x)) = G(x)\nabla F(x) = G(x) F^{'}(x)$

$\nabla^2_F(F(x)G(x)) = G(x)\nabla^2 F(x) = G(x) F^{''}(x)$

$\overset{\wedge}{I}$ — :

$\overset{\wedge}{I} f_n = f_n$

$\overset{\displaystyle\epsilon}{'}$ — - :

$f_k^\overset{\displaystyle\epsilon}{'} = (f_{k+1} - f_k)/\epsilon$

$\overset{\displaystyle\epsilon}{\nabla}_f$ — , , - ,

$f$ ( -

$f$ ) () , ,

$\overset{\displaystyle\epsilon}{\nabla}_f{(f_n g_n)} = g_n\overset{\displaystyle\epsilon}{\nabla}f_n$

$\overset{\displaystyle\epsilon}{\nabla^2}_f{(f_n g_n)} = g_n\overset{\displaystyle\epsilon}{\nabla^2}f_n$

$\overset{\displaystyle\epsilon}{*}$ —

$f^{\overset{\displaystyle\epsilon}{\displaystyle i}}$ —

$i$ - -

$f$ . , ,

$f^{\overset{\displaystyle\epsilon}{ 2}} = f\displaystyle\overset{\displaystyle\epsilon}{*}{f}$

$f^{\overset{\displaystyle\epsilon}{\displaystyle (i)}}$ —

$i$ - -

$f$ . , ,

$f^{\overset{\displaystyle\epsilon}{ (2)}} = (f\displaystyle\overset{\displaystyle\epsilon}{'})\displaystyle\overset{\displaystyle\epsilon}{'}$

$\overset{\epsilon}{\rightarrow}$ — - ()

$F(x) \overset{\epsilon}{\rightarrow} f_n$ ,

$F(x)$

$f_n$ -,

$f_n$ -

$F(x)$

$F(x)$ — -

$f_n$

$\overset{\epsilon}{\leftarrow}$ — -

Logika singkat dari artikel

. - .

$f_n, g_n,p_n$ ,…, $\{0,\epsilon,2\epsilon,\ldots\}$ , $\epsilon \in R$ , $\epsilon>0$ .

$\epsilon$ . , , $\epsilon \to 0$ , $\epsilon = 1$
:
$\overset{\displaystyle\epsilon}{\nabla}{f_n} = (f_{n+1} - f_n)/\epsilon$ , $\epsilon$ —
, - fnϵ∗gn.

-:
pk=(fϵ∗g)k=(ϵ(ϵ∇f+ϵ∇g)+∧I)k(fg)|0

pk=(fϵ∗g)k=k∑j=0Cjkj∑i=0Cijfϵ(i)|0gϵ(j−i)|0

pk=(fϵ∗g)k=∑j+i+l=kCj,ikfigj(−1)l

Cj,ik — : Cj,ik=k!j!i!l!, (l+j+i=k)
:
- , , , , () ()
- - , () :
  
  $\overset{\displaystyle\epsilon}{\nabla} (f_n \overset{\displaystyle\epsilon}{*}g_n) = \overset{\displaystyle\epsilon}{\nabla} f_n \overset{\displaystyle\epsilon}{*}g_n + f_n \overset{\displaystyle\epsilon}{*}\overset{\displaystyle\epsilon}{\nabla} g_n$
- $\epsilon \rightarrow 0$ ( ) - $F(x)G(x)$ , $F(x)$ $G(x)$ , $f_n$ $g_n$ $\epsilon \rightarrow 0$ , :
  
  $F(x) = \lim\limits_{\epsilon \rightarrow 0, k\epsilon = x} f_k$
  $G(x) = \lim\limits_{\epsilon \rightarrow 0, k\epsilon = x} g_k$
  
  $F(x)$ $f_n$ , $G(x)$ $g_n$ -
- . , , -, - -:

$f_k=f_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{1}}}{1!}{f\overset{\displaystyle\epsilon}{'}}_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{2}}}{2!}{f^{\overset{\displaystyle\epsilon}{(2)}}}_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{3}}}{3!}{f^{\overset{\displaystyle\epsilon}{(3)}}}_0+\ldots+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{k}}}{k!}{f^{\overset{\displaystyle\epsilon}{(k)}}}_0$
- -, (, - ). , - ( ) - () . - $\epsilon$ . , , - :

$\epsilon exp(k\epsilon)=1+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{1}}}{1!}+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{2}}}{2!} +\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{3}}}{3!}+\ldots+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{k}}}{k!}$
. (, , ) - -. . , , - . ,

$\epsilon cos^{\overset{\displaystyle\epsilon}{2}}(k\epsilon) +\epsilon sin^{\overset{\displaystyle\epsilon}{2}}(k\epsilon) = 1$

$\overset{\displaystyle\epsilon}{\rightarrow}$ , ,

$cos^2(x) + sin^2(x) = 1$ $\overset{\displaystyle\epsilon}{\rightarrow}$ $\epsilon cos^{\overset{\displaystyle \epsilon}{2}}(k\epsilon) +\epsilon sin^{\overset{\displaystyle\epsilon}{2}}(k\epsilon) = 1$

- -. - - . - -. (, - ) -.
, - — () -. , $\overset{\displaystyle\epsilon}{\leftarrow}$ .
, - () ( ) ().

:

$\overset{\displaystyle\epsilon}{\rightarrow}$ $\rightarrow$ $f_n$ ( ) $\overset{\displaystyle\epsilon}{\leftarrow}$ $F(x)$ ( )

, - , C, -, . , , , . , , , .
, . :

C $\overset{\displaystyle\epsilon}{\leftarrow}$ $\rightarrow$ $F(x)$ ( ) $\overset{\displaystyle\epsilon}{ \rightarrow}$ $f_n$ ( C)
, , , - -
- ()
- ( )
$\epsilon \rightarrow 0$ ( ) - - . , , $\epsilon \rightarrow 0$ , - — ,… - — , - … , - $\epsilon \rightarrow 0$ . - ( ) , $\epsilon \rightarrow 0$ .
, - «» ( ) ? , , :

$i\hbar\frac{\partial}{\partial t}\Psi(x,t)=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\Psi(x,t) + U(x,t )\Psi(x,t)$

$\Delta x$ $\Delta t$ ( , ), , .

- ( -, -, — -, ...). $\epsilon$ , . -, .
, , «» , -? ?

Fungsi kisi dan turunan epsilon

Fungsi dan set kisi

$A^\epsilon$

Fungsi kisi adalah fungsi yang didefinisikan pada himpunan bilangan real diskrit dengan langkah konstan. Kami hanya akan mempertimbangkan fungsi yang ditentukan pada set

$\{0,\epsilon,2\epsilon,3\epsilon,\ldots\}$ dimana

$\epsilon \in R$ ,

$\epsilon>0$ . Jadi, misalnya, fungsi seperti itu

$cos(0.1k\pi)$ dimana

$k$ Merupakan bilangan bulat non-negatif. Di mana

$\epsilon = 0.1\pi$ . Kami menunjukkan set fungsi tersebut oleh

$A^\epsilon$ . Semua fungsi kisi yang akan kita pertimbangkan di bawah akan menjadi milik set ini

$A^\epsilon$ .

Contoh Fungsi Kisi $\in A^\epsilon$

Fungsi

$cos(0.1k\pi)$ dimana

$k \i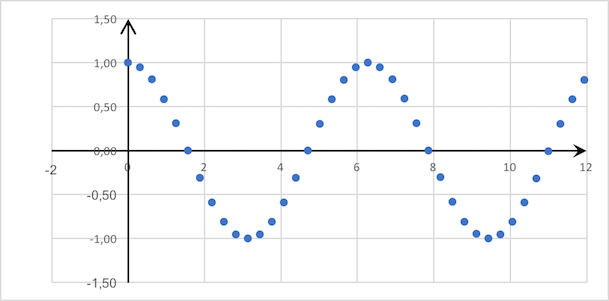n N_0$ :

Turunan Epsilon

Kami akan memanggil fungsi turunan epsilon

$f \in A^\epsilon$ di

$k$ nilai berikut:

$f\overset{\displaystyle\epsilon}{'}_k = \overset{\displaystyle\epsilon}{\nabla}{f_k} = (f_{k+1} - f_k)/\epsilon$

Dengan demikian, fungsi yang nilainya dalam

$k$ untuk siapa saja

$k$ sama dengan fungsi turunan epsilon

$f_n$ di

$k$ kita akan memanggil fungsi turunan epsilon

$f_n$ dan dilambangkan sebagai

$f_n\overset{\displaystyle\epsilon}{'}$ (atau sederhana

$f\overset{\displaystyle\epsilon}{'}$ )

Jelas, fungsinya

$f^{\overset{\displaystyle\epsilon}{'}}\in$

$A^\epsilon$ dan karena itu, diferensiasi epsilon dapat diterapkan lagi, dll. Kami akan menunjukkan oleh

$^{\overset{\displaystyle\epsilon}{(n)}}$

$n$ -Yu

$\epsilon$ - Fungsi derivatif. Sangat mudah dibuktikan dengan induksi itu

$f^{\overset{\displaystyle\epsilon}{(n)}}_k=\displaystyle\frac{1}{\epsilon^n}\sum\limits_{j=0}^{n}C_{n}^{j}f_{k+j}(-1)^{n-j}$

Integrasi Epsilon

Prosedur yang berlawanan dengan diferensiasi epsilon disebut integrasi epsilon, masing-masing. Fungsi

$g_n\in A^\epsilon$ yang nilainya dalam

$k$ untuk siapa saja

$k$

$g_k=\epsilon\sum\limits^{k-1}_{i=0}f_i+C$

akan memanggil fungsi primitif epsilon

$f$ .

Turunan Epsilon dari produk

Sayangnya, turunan epsilon tidak memiliki sifat turunan biasa. Jadi, misalnya, jelas bahwa dalam kasus umum

$(f_n g_n)^{\overset{\displaystyle\epsilon}{'}} = f_n^{\overset{\displaystyle\epsilon}{'}}g_n+g_n^{\overset{\displaystyle\epsilon}{'}}f_n +\epsilon f_n^{\overset{\displaystyle\epsilon}{'}} g_n^{\overset{\displaystyle\epsilon}{'}}\neq f_n^{\overset{\displaystyle\epsilon}{'}}g_n+g_n^{\overset{\displaystyle\epsilon}{'}}f_n$

Bagian

$\epsilon f_n^{\overset{\displaystyle\epsilon}{'}} g_n^{\overset{\displaystyle\epsilon}{'}}$ membedakan "turunan" ini dari turunan biasa dari produk fungsi terdiferensiasi. Dalam kasus penyelesaian persamaan diferensial nonlinier dengan metode numerik, ini memberikan kesalahan tambahan dalam perhitungan.

Keterangan.

Istilah tambahan ini juga lead, khususnya, untuk fakta bahwa kita tidak dapat menerapkan biasa Taylor rumus untuk memperluas fungsi kisi dalam seri

Sekarang mari kita bayangkan bahwa kita tidak akan memiliki anggota tambahan ini. Sehingga ini bisa memberi kita?

Setidaknya, kita bisa menerapkan beberapa metode untuk menyelesaikan persamaan diferensial untuk menyelesaikan persamaan perulangan (persamaan dengan fungsi dari set

$A^\epsilon$ ) Sebagai contoh, kita akan memperluas ke seri Taylor, kita bisa menggunakan integrasi (epsilon-integrasi) di bagian, menerapkan transformasi (epsilon-transformasi) dari Laplace. Namun pada kenyataannya, semuanya bahkan lebih menarik, dan artikel ini didedikasikan untuk ini.

Tetapi bagaimana cara menghilangkan elemen tambahan ini? Kita dapat membuat, misalnya, perkalian lain (epsilon-perkalian).

Masalah dasar

Inilah tepatnya masalah, solusi yang merupakan keseluruhan artikel.

Kami ingin mencari formula untuk produk epsilon

$p_k=(f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k$ untuk memenuhi persyaratan berikut:

sifat-sifat perkalian biasa akan terpenuhi, seperti komutatifitas, asosiatifitas, distributivitas, keberadaan unit (tunggal) dan elemen nol (tunggal)
untuk turunan epsilon dari produk epsilon dari fungsi kisi, kita harus memiliki formula yang sama dengan turunan dari produk fungsi terdiferensiasi, yaitu

$\overset{\displaystyle\epsilon}{\nabla} (f_n \overset{\displaystyle\epsilon}{*}g_n) = \overset{\displaystyle\epsilon}{\nabla} f_n \overset{\displaystyle\epsilon}{*}g_n + f_n \overset{\displaystyle\epsilon}{*}\overset{\displaystyle\epsilon}{\nabla} g_n$
sambil berjuang $\epsilon \rightarrow 0$ (langkah fungsi kisi) produk epsilon harus cenderung ke produk biasa $F(x)G(x)$ dimana $F(x)$ dan $G(x)$ masing-masing fungsi yang cenderung fungsi kisi $f_n$ dan $g_n$ di $\epsilon \rightarrow 0$ , yaitu:

$F(x) = \lim\limits_{\epsilon \rightarrow 0, k\epsilon = x} f_k$
$G(x) = \lim\limits_{\epsilon \rightarrow 0, k\epsilon = x} g_k$

Penggandaan Epsilon

Fungsi ini memenuhi semua properti ini.

$p_k$ didefinisikan sebagai (ketiga formula itu setara):

$p_k=(f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=(\epsilon({{\overset{\displaystyle\epsilon}{\nabla}}_{f}}+{{\overset{\displaystyle\epsilon}{\nabla}}_{g}})+{\overset{\wedge}{I}})^k (f g)|_0$

$p_k = (f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=\sum_{j=0}^{k}C_{k}^{j}\sum_{i=0}^{j}C_{j}^{i}{f^{\overset{\displaystyle\epsilon}{(i)}}}|_0{g^{\overset{\displaystyle\epsilon}{(j-i)}}}|_0$

$p_k=(f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=\sum_{j+i+l=k}C_k^{j,i}f_ig_j(-1)^{l}$ ,
di mana

$C_{k}^{j,i}$ - koefisien binomial Newton:

$C_{k}^{j,i}=\displaystyle\frac{k!}{j!i!l!}$ , (

$l+j+i=k$ )

Catatan

Agar tidak membebani artikel, kami tidak akan memberikan bukti, tetapi dua properti pertama mudah dibuktikan, yang terakhir tidak begitu jelas

Untuk sedikit merasa nyaman dengan karya baru, pertimbangkan beberapa contoh.

Contoh 1. (perkalian dengan angka)

$f_n\in A^{\epsilon}$

$f_k = \lambda$ ,

$\lambda$ — ,

$g_k \in A^{\epsilon}$ -

$p =f\displaystyle\overset{\displaystyle\epsilon}{*}g$

$p_k = \lambda g_k$ .

-.

, -

$f_n \in A^\epsilon$ 1, — 0.

Contoh 2. (tingkat epsilon)

- -

$f_k = (k\epsilon)^{\overset{\displaystyle\epsilon}{i}}$ , - ( -)

$F(x) = x^i$ :

$x^{\overset{\displaystyle\epsilon}{i}} = (k\epsilon)^{\overset{\displaystyle\epsilon}{i}}=i!C_k^i\epsilon^i$

, - ( -)

$x^i=(k\epsilon)^i$

$i!C_k^i\epsilon^i$

, ,

$x^{\overset{\displaystyle\epsilon}{2}} = (k\epsilon)^{\overset{\displaystyle\epsilon}{2}}=k(k-1)\epsilon^2$

$x^{\overset{\displaystyle\epsilon}{3}} = (k\epsilon)^{\overset{\displaystyle\epsilon}{3}}=k(k-1)(k-2)\epsilon^3$

,

$(k\epsilon)^{\overset{\displaystyle\epsilon}{i}}$

$i>k$

- - , ,

$(k^{\overset{\displaystyle\epsilon}{i}})^{\overset{\displaystyle\epsilon}{'}}=ik^{\overset{\displaystyle\epsilon}{i-1}}$

$\epsilon$ , , .. $\epsilon$ ( $\epsilon >0$ , $\epsilon \in R$ ), 1. , $\epsilon$ , , , $\epsilon \to 0$

Epsilon Taylor Series

Sekarang kami memiliki analog lengkap dari ekspansi Taylor:

$f_k=f_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{1}}}{1!}{f\overset{\displaystyle\epsilon}{'}}_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{2}}}{2!}{f^{\overset{\displaystyle\epsilon}{(2)}}}_0+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{3}}}{3!}{f^{\overset{\displaystyle\epsilon}{(3)}}}_0+\ldots+\displaystyle\frac{(k\epsilon)^{\overset{\displaystyle\epsilon}{k}}}{k!}{f^{\overset{\displaystyle\epsilon}{(k)}}}_0$

Kita akan menyebut seri ini seri epsilon dari Taylor, dan dekomposisi itu sendiri akan disebut seri epsilon dalam seri Taylor.

Konversi Epsilon

Definisi (Transformasi Epsilon)

Biarkan

$\exists x_0 >0$ sedemikian rupa sehingga di set

$[0,x_0)$ Serangkaian fungsi Taylor

$F(x)$ di lingkungan kanan nol konvergen ke fungsi itu sendiri. Lalu fungsinya

$F(x)$ kita akan memanggil fungsi analitik nol di sebelah kanan. Lalu fungsinya

$F$ dan

$f\in A^\epsilon$ akan disebut epsilon-konjugat jika bilangan bulat atau nol

$i$

$i$ turunan yang tepat

$F$ nol sama dengan

$i$ fungsi turunan epsilon

$f$ nol.

$F^{(i)}|_{+0}=f^{\overset{\displaystyle\epsilon}{(i)}}_0, \forall i \in N_0$

Fungsi

$f$ maka kita akan memanggil gambar epsilon

$F$ atau jika fungsi ini memiliki nama (misalnya, cos), maka kita cukup memanggil epsilon "nama fungsi" (misalnya, epsilon-cosinus) dan menyatakannya sebagai

$\epsilon$ `` sebutan fungsi '' (

$\epsilon$ cos). Fungsi

$F$ kita sebut epsilon inverse dari fungsi

$f$ .

Contoh 1. (peserta pameran Epsilon)

$\epsilon{\exp}$ .

$\sigma$ . -

$\exp(\sigma x)$

$\epsilon exp(\sigma x)_k=1+C_k^1\sigma \epsilon+C_k^2(\sigma \epsilon)^2+\ldots+C_k^k(\sigma\epsilon)^k=(1+\sigma \epsilon)^k$

,

$(1+ \sigma x/k)^k\overset{k\to\infty}{\to}\exp(\sigma x)$

,

$\epsilon = x/k \to 0$ , ( ):

$\epsilon exp(\sigma x) \overset{\epsilon\to\ 0}{\to} \exp(\sigma x)$

-.

Contoh 2. (Epsilon-cosinus, Epsilon-sinus)

- -.

$\lambda$ — . T

$\epsilon{\cos(\lambda x)}_k=\frac{1}{2}((1+i\lambda\epsilon)^k+(1-i\lambda\epsilon)^k)$

$\epsilon{\cos(\lambda x)}\overset{\epsilon\to0}{\to}\cos{(\lambda x)}$

$\epsilon{\sin(\lambda x)}_k=\frac{1}{2i}((1+i\lambda \epsilon)^k-(1-i\lambda \epsilon)^k)$

$\epsilon{\sin(\lambda x)}\overset{\epsilon\to0}{\to}\sin{(\lambda x)}$

Contoh 3. (Penggandaan Epsilon dengan X pada derajat epsilon)

$f_n \overset{\displaystyle \epsilon}{*} x^{\overset{\displaystyle\epsilon}{\lambda}}$

$\lambda$ —

$x^\lambda F(x)$

$(x^\lambda F(x))^{(n)}|_{x = 0} = \sum\limits_{j=0}^{\infty}C^j_n (x^\lambda)^{(j)}F^{(n-j)}(x) |_{x = 0} = C_n^\lambda \lambda! F^{(n-\lambda)}(x) |_{x = 0}$

- -

$f_n \overset{\displaystyle \epsilon}{*} x^{\overset{\displaystyle\epsilon}{\lambda}} = f_{n - \lambda } x^{\overset{\displaystyle\epsilon}{\lambda}}$

,

$\lambda$ , ,

$\lambda$

Operasi Transformasi Epsilon

Dalam tabel ini dan dalam fungsi berikut

$F(x)$ dan

$f_n$ , dan

$G(x)$ dan

$g_n$ - dipasangkan epsilon-konjugat, mis.

$F(x) \overset{\epsilon}\to f_n$

$G(x) \overset{\epsilon}\to g_n$

Kemudian operasi dikonversi (sebagai hasil dari konversi epsilon) sebagai berikut:

$F(x) \equiv G(x)$

$\overset{\epsilon} {\to}$

$f_n \equiv g_n$

$F(x) + G(x)$

$\overset{\epsilon} {\to}$

$f_n + g_n$

$F(x) G(x)$

$\overset{\epsilon} {\to}$

$f_n \displaystyle\overset\epsilon{*} g_n$

$F'(x)$

$\overset{\epsilon} {\to}$

$f \displaystyle\overset\epsilon{'}_n$

$\int F(x)dx$

$\overset{\epsilon} {\to}$

$\epsilon\sum\limits^{k-1}_{i=0}f_i$ (epsilon primitif)

transformasi epsilon dari beberapa fungsi analitik

$F(x) \equiv \lambda$

$\overset{\epsilon} {\to}$

$f_n \equiv \lambda$

$\lambda F(x)$

$\overset{\epsilon} {\to}$

$\lambda f_n$

$x^i$

$\overset{\epsilon} {\to}$

$(k\epsilon)^{\overset{\displaystyle\epsilon}{i}}=i!C_k^i\epsilon^i$

$\exp(\lambda x)$

$\overset{\epsilon} {\to}$

$\epsilon exp(\lambda x)_k=(1+\lambda \epsilon)^k$

$\cos(\lambda x)$

$\overset{\epsilon} {\to}$

$\epsilon{\cos(\lambda x)}_k=\frac{1}{2}((1+i\lambda\epsilon)^k+(1-i\lambda\epsilon)^k)$

$\sin(\lambda x)$

$\overset{\epsilon} {\to}$

$\epsilon{\sin(\lambda x)}_k=\frac{1}{2i}((1+i\lambda \epsilon)^k-(1-i\lambda \epsilon)^k)$

$(1 + \lambda x)^{-1}$

$\overset{\epsilon} {\to}$

$(1+\lambda x)^{\overset{\displaystyle\epsilon}{-1}}=1-\lambda x +\lambda^2 x^{\overset{\displaystyle\epsilon}{2}}-\lambda^3x^{\overset{\displaystyle\epsilon}{3}}+...$ (untuk

$|\lambda x| < 1$ A)

ekspansi Taylor epsilon

$f_k = (1 + \epsilon \overset{\epsilon}{\nabla})^k f|_{k=0}=f_0+\displaystyle\frac{(\epsilon k)^{\overset{\displaystyle\epsilon}{1}}}{1!}{f\overset{\displaystyle\epsilon}{'}}_0+\displaystyle\frac{(\epsilon k)^{\overset{\displaystyle\epsilon}{2}}}{2!}{f^{\overset{\displaystyle\epsilon}{(2)}}}_0+\displaystyle\frac{(\epsilon k)^{\overset{\displaystyle\epsilon}{3}}}{3!}{f^{\overset{\displaystyle\epsilon}{(3)}}}_0+\ldots+\displaystyle\frac{(\epsilon k)^{\overset{\displaystyle\epsilon}{k}}}{k!}{f^{\overset{\displaystyle\epsilon}{(k)}}}_0$

Formula ini menjadi jelas jika kita perhatikan operatornya

$(1 + \epsilon \overset{\epsilon}{\nabla})^i$ adalah operator offset

$i$ Langkah:

$(1 + \epsilon \overset{\epsilon}{\nabla})^i f_k = f_{k+i}$

Transformasi Epsilon Laplace

Kami juga dapat memperkenalkan transformasi Epsilon Laplace dan menggunakannya serta Transformasi Laplace biasa sehubungan dengan fungsi kisi

$\in A^\epsilon$ tapi ini di luar cakupan artikel ini.

Transformasi Epsilon untuk Rumus Trigonometrik

Mengingat hal tersebut di atas, kita dapat menulis, misalnya, analog dari rumus trigonometri

${\epsilon{\cos(x)}}^{\overset{\displaystyle\epsilon}{2}}+{\displaystyle\epsilon{\sin(x)}}^{\overset{\displaystyle\epsilon}{2}}\equiv 1$

${\epsilon{\cos(x)}}{\overset{\displaystyle\epsilon}{'}}\equiv-\epsilon{\sin(x)}$

${\epsilon{\sin(x)}}{\overset{\displaystyle\epsilon}{'}}\equiv\epsilon{\cos(x)}$

${\epsilon{\cos(\alpha+\beta)}}\equiv{\epsilon{\cos(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\cos(\beta)}}-{\epsilon{\sin(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\sin(\beta)}}$

${\epsilon{\cos(\alpha-\beta)}}\equiv{\epsilon{\cos(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\cos(\beta)}}+{\epsilon{\sin(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\sin(\beta)}}$

${\epsilon{\sin(\alpha+\beta)}}\equiv{\epsilon{\sin(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\cos(\beta)}}+{\epsilon{\cos(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\sin(\beta)}}$

${\epsilon{\sin(\alpha-\beta)}}\equiv{\epsilon{\sin(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\cos(\beta)}}-{\epsilon{\cos(\alpha)}}\displaystyle\overset{\displaystyle\epsilon}{*}{\epsilon{\sin(\beta)}}$

Namun demikian, epsilon-cosinus dan epsilon-sinus tidak, tidak seperti cosinus dan sinus biasa, memiliki satu fitur penting - mereka tidak periodik. Betulkah,

$\epsilon{\cos(\omega t)}_k=\frac{1}{2}((1+i\omega \epsilon)^k+(1-i\omega \epsilon)^k)=\left({\sqrt{1+(\omega \epsilon)^2}}\right)^k \cos{(k(arctg(\omega \epsilon)))}$

$\epsilon{\cos(\omega t)}_{\frac{t}{\epsilon}}=\left({{1+\omega^2 \epsilon^2}}\right)^{\frac{t}{2\epsilon}}\cos{(t \displaystyle \frac{arct(\omega \epsilon)}{ \epsilon})}$

Juga

$\epsilon{sin(\omega t)}_{\frac{t}{\epsilon}}=\left({{1+\omega^2 \epsilon^2}}\right)^{\frac{t}{2\epsilon}}\sin{(t \displaystyle \frac{arctg(\omega \epsilon)}{ \epsilon})}$

pada saat bersamaan fungsinya

$sin( t(arctg(\omega \epsilon)/\epsilon))$ dan

$\cos(t(arctg(\omega\epsilon/)\epsilon))$ - fungsi periodik dengan titik

$2\pi\epsilon/arctg(\omega \epsilon)$ . Karena itu fungsinya

$\epsilon{\cos(x)}$ dan

$\epsilon{\sin(x)}$ - fungsi non-periodik, dengan nol di titik

$(\pi/2+\pi n)\epsilon/arctg(\omega \epsilon)$ dan

$\pi n\epsilon/arctg(\omega \epsilon)$ dengan demikian, dalam hal ini, `` range '' antara minima dan maxima saat terbawa

$t$ meningkat sebagai

$({1+\omega^2\epsilon^2})^{\frac{t}{2\epsilon}}$ .

Berkomentar

demikian, untuk epsilon eksponen kita memiliki

$\epsilon{exp(i\omega t)}_{\frac{t}{\epsilon}}=\left({{1+\omega^2 \epsilon^2}}\right)^{\frac{t}{2\epsilon}}\exp{(i \displaystyle \frac{arctg(\omega \epsilon)}{ \epsilon}t)}$

Contoh pemecahan persamaan diferensial dengan metode pemetaan epsilon

Contoh 1. Osilasi harmonis

$F^{''}(t) + \omega^2 F(t) = 0$

.

1. ( )

$\epsilon^2 f^\overset{\displaystyle\epsilon}{(2)} + \epsilon^2\omega^2 f = f_{k+2} - 2f_{k+1} + (1+ \epsilon^2\omega^2)f_{k} = f_{k+2} - 2f_{k+1} + \lambda f_{k}\equiv 0$

$\lambda = 1+\epsilon^2 \omega^2$ .

.

, , , .

, , .

2. . (- )

$n$ - - - .

$(f^{\overset{\displaystyle\epsilon}{(2)}}+ \omega^2 f)^{\overset{\displaystyle\epsilon}{(n)}} = f^{\overset{\displaystyle\epsilon}{(n+2)}} + \omega^2 f^{\overset{\displaystyle\epsilon}{(n)}} \equiv 0$

$f^{\overset{\displaystyle\epsilon}{(n+2)}}|_0 + \omega^2 f^{\overset{\displaystyle\epsilon}{(n)}}|_0 = 0$

3. . ( )

,

$f_0 = F(0)$ ,

$(f_1 - f_0)/\epsilon = F'(t)|_{t=0}$ .

,

$F(0) = 0$ ,

$F'(0) = 1$ . :

$f^{\overset{\displaystyle\epsilon}{(2k)}}|_0 = 0$

$f^{\overset{\displaystyle\epsilon}{(2k+1)}}|_0 = (-1)^k\omega^{2k}$

4. . ( )

$F(x) = \sum\limits_{k=0}^{\infty} (-1)^k\displaystyle{\frac{\omega^{2k}t^{2k+1}}{(2k+1)!}} = \displaystyle\frac{1}{\omega}\sin(\omega t)$

( ),

2. . ( $f_k$ )

$\epsilon$ $\lambda$ , $\lambda$ , $\epsilon$ $\in R$ , , $\epsilon = 1$

$k$ , 0. , , , , .

, , ,

$F(0) = 0$ , 1. :

$f_0 = 0$

$f_1 = \epsilon$

$f_2 = 2f_1 - \lambda f_0 = 2\epsilon$

$f_3 = 2f_2 - \lambda f_1 = \epsilon(4 -\lambda)$

$f_4 = 2f_3 - \lambda f_2 = 2\epsilon(4 -\lambda) -2 \epsilon\lambda = \epsilon(8 - 4\lambda)$

$f_5 = 2f_4 - \lambda f_3 = \epsilon(2(8 -4\lambda) -\lambda (4- \lambda)) = \epsilon(\lambda^2 - 12\lambda +16)$

…

3. . (- )

$f_0 = 0$

$f^\overset{\displaystyle\epsilon}{'}|_0 = (f_1 -f_0)/\epsilon = 1$

$f^\overset{\displaystyle\epsilon}{(2)}|_0 = f_2 - 2f_1 +f_0 = 0$

$f^\overset{\displaystyle\epsilon}{(3)}|_0 =\epsilon(f_3 -3f_2 + 3f_1 - f_0)/\epsilon^3 = (4 - \lambda - 6 + 3 - 0)/\epsilon^2 = (1 - \lambda)/\epsilon^2 = - \omega^2$

$f^\overset{\displaystyle\epsilon}{(4)}|_0 =(f_4 - 4f_3 +6f_2 - 4f_1 + f_0)/\epsilon^4 = (8 - 4\lambda - 4(4-\lambda) + 12 - 4)/\epsilon^3 = 0$

$f^\overset{\displaystyle\epsilon}{(5)}|_0 = ... = \omega^4$

…

4. . ( )

( , ) , - , :

$F(x) = f_0 + \displaystyle\frac{f^{\overset{\displaystyle\epsilon}{(1)}}|_0}{1!}x + \displaystyle\frac{f^{\overset{\displaystyle\epsilon}{(2)}}|_0}{2!}x^2 + \displaystyle\frac{f^{\overset{\displaystyle\epsilon}{(3)}}|_0}{3!}x^3 + \displaystyle\frac{f^{\overset{\displaystyle\epsilon}{(4)}}|_0}{4!}x^4 + \displaystyle\frac{f^{\overset{\displaystyle\epsilon}{(5)}}|_0}{5!}x^5 + ...$

$F(x) = t - \displaystyle\frac{\omega^2}{3!}t^3 + \displaystyle\frac{\omega^4}{5!}t^5 + ...$

.

, , -, , ,

Contoh 2. Persamaan Bessel

- . , , .

$x^2F''+xF'+(x^2-\mu^2)F\equiv 0$

1. ( )

$x^{\overset{\displaystyle\epsilon}{2}}\overset{\displaystyle\epsilon}{*}f^{\overset{\displaystyle\epsilon}{(2)}}+x\overset{\displaystyle\epsilon}{*}f^{\overset{\displaystyle\epsilon}{(1)}}+(x^{\overset{\displaystyle\epsilon}{2}}-\mu^2)\overset{\displaystyle\epsilon}{*}f\equiv0$

$x^{\overset{\displaystyle\epsilon}{2}}f_{n-2}^{\overset{\displaystyle\epsilon}{(2)}}+xf_{n-1}^{\overset{\displaystyle\epsilon}{(1)}}+x^{\overset{\displaystyle\epsilon}{2}}f_{n-2}- \mu^2 f\equiv0$

2. . (- )

$\epsilon =1$

$n$ - - .

$2\displaystyle\frac{n(n-1)}{2!}f_0^{\overset{\displaystyle\epsilon}{(n)}}+nf_0^{\overset{\displaystyle\epsilon}{(n)}}+2\frac{n(n-1)}{2!}f_0^{\overset{\displaystyle\epsilon}{(n-2)}}-\mu^2f_0^{\overset{\displaystyle\epsilon}{(n)}} =0$

$(n^2-\mu^2)f_0^{\overset{\displaystyle\epsilon}{(n)}}=-n(n-1)f_0^{\overset{\displaystyle\epsilon}{(n-2)}}$

3. . ( )

-

$f$ :

$\mu^2f_0 = 0$

$f^{\overset{\displaystyle\epsilon}{(1)}}= f_0\displaystyle\frac{\mu^2}{1 - \mu^2}$

$f^{\overset{\displaystyle\epsilon}{(2)}}= - f_0\displaystyle\frac{2}{(4-\mu^2)}$

…

$f_0^{\overset{\displaystyle\epsilon}{(n)}}=- f_0^{\overset{\displaystyle\epsilon}{(n-2)}}\displaystyle\frac{n(n-1)}{n^2-\mu^2}$

$b_n$ —

$n$ - - .

$b_n =- \displaystyle\frac{b_{n-2}}{n^2-\mu^2}$

,

$\mu$ 0, T 0.

$\mu$ , ,

$\mu$ - - T .

$n = 2k+\mu$ - 0,

$n = 2k -1 +\mu$ (

$k$ — ) — 0.

$2k+\mu$ — - .

$2k + \mu$

$n$

$b_{2k+\mu} =- \displaystyle\frac{b_{2(k-1) +\mu}}{4k(k+\mu)}$

,

$2k+\mu$ - - T

$b_{2k+\mu}=C\displaystyle{\frac{(-1)^k}{k!(k+\mu)!2^{2k+\mu}}}$

$\mu$ - , C- ,

4. . ( )

$\mu$ ,

$C = 1$

$F(x)=\sum_\limits{k=0}^{\infty}{\displaystyle{\frac{(-1)^k}{k!(k+\mu)!}\left(\frac{x}{2}\right)^{2k+\mu}}}$

,

$\mu$ .

— T .

Contoh 3. Angka-angka Fibonacci

, -.

, :

$f_{k+2}=f_k+f_{k+1}$ ,
,

$f_0=0$ ,

$f_1=1$ , ,

$f_0\overset{\displaystyle\epsilon}{'}=1/\epsilon$

$f_k+2\epsilon f_k^{\overset{\displaystyle{\epsilon}}{(1)}}+\epsilon^2f_k^{\overset{\displaystyle{\epsilon}}{(2)}}=f_k+f_k+\epsilon f_k^{\overset{\displaystyle{\epsilon}}{(1)}}$

$f-\epsilon f^{\overset{\displaystyle{\epsilon}}{(1)}}-\epsilon^2f^{\overset{\displaystyle{\epsilon}}{(2)}}=0$

,

$\epsilon=1$ . T

$f-f^{\overset{\displaystyle{\epsilon}}{(1)}}-f^{\overset{\displaystyle{\epsilon}}{(2)}}=0$ ,

$f_0=0$

$f_0\overset{\displaystyle\epsilon}{'}=1$

1. ( -)

-

$F-F'-F''=0$

$F(+0)=0$ ,

$F'(+0)=1$

2. ( )

. .

$p^2L(p)-0-1+p L(p)+0-L(p)=0$

$L(p)=\displaystyle{\frac{1}{(p^2+p-1)}}=\displaystyle{\frac{1}{(p_1-p_2)} \left[\frac{1}{p-p_1}-\frac{1}{p-p_2}\right]}$ ,

$p_1$ ,

$p_2$ —

$p^2+p-1=0$ :

$p_1=(-1+\sqrt{5})/2$

$p_2=(-1-\sqrt{5})/2$ .

$F(x)=\displaystyle{\frac{1}{\sqrt{5}}}(\exp{(p_1x)}-\exp{(p_2x)})$ .

3. ( -)

, -

$F$ .

$f_k=\displaystyle{\frac{1}{\sqrt{5}}}(\epsilon{\exp{(p_1x)}}-\epsilon{\exp{(p_2x)}})=\displaystyle{{\frac{\left((1+\epsilon\frac{-1+\sqrt{5}}{2})^k-\left(-1+\epsilon\frac{1-\sqrt{5}}{2}\right)^k\right)}{\sqrt{5}}}}$

,

$\epsilon=1$

$f_k=\displaystyle{{\frac{\left(\left(\frac{1+\sqrt{5}}{2}\right)^k-\left(\frac{1-\sqrt{5}}{2}\right)^k\right)}{\sqrt{5}}}}$

Properti pemetaan Epsilon sebagai ε → 0

Membalikkan konversi epsilon dapat dilakukan hanya dengan mengarahkan

$\epsilon \to 0$

Ini dapat dirumuskan lebih ketat dalam bentuk teorema, yang akan saya berikan tanpa bukti.

Teorema

Biarkan Fungsinya

$F$ dan

$f$ - epsilon-konjugat untuk apa saja

$\epsilon$ . Lalu, sambil berjuang

$\epsilon \to 0$ , dengan ketentuan

$k\epsilon=const=a\in(0,x_0)$ (Dimana

$x_0$ memiliki arti yang sama dengan definisi pemetaan epsilon), nilainya

$f_k$ di lokasi syuting

$(0,x_0)$ berniat untuk

$F(a)$ , yaitu

$\lim\limits_{\epsilon \to0, k\epsilon=a}f(k\epsilon)=F(a)$

Fungsi non analitik

pembagian oleh x dalam derajat epsilon

( ) .

«» ?

, -

$\displaystyle\frac{1}{x^\lambda}$ ,

$\lambda$ — . 0. -

$x^\overset{\displaystyle\epsilon}{-\lambda}$ .

$g_n = x^\overset{\displaystyle\epsilon}{-\lambda} \overset{\displaystyle\epsilon}{*} f_n$

$x^{\overset{\displaystyle\epsilon}{\lambda}} \overset{\displaystyle\epsilon}{*} g_n = f_n$

$x^{\overset{\displaystyle\epsilon}{\lambda}} \overset{\displaystyle\epsilon}{*} g_n = x^\overset{\displaystyle\epsilon}{\lambda}g_{n-\lambda}$

$g_{n-\lambda} = f_n/x^\overset{\displaystyle\epsilon}{\lambda} =\displaystyle\frac {f_n}{n(n-1)..(n-\lambda + 1)}$

$g_n = x^\overset{\displaystyle\epsilon}{-\lambda} \overset{\displaystyle\epsilon}{*} f_n =\displaystyle\frac {n!f_{n + \lambda}}{(n+\lambda)!}$

$f_n = \overset{\wedge}{I}$ , ,

$x^\overset{\displaystyle\epsilon}{-\lambda} = \displaystyle\frac {n!}{(n+\lambda)!}$ , ,

$x^\overset{\displaystyle\epsilon}{\lambda} = \displaystyle\frac {n!}{(n-\lambda)!}$

$\lambda$ (

$\lambda \in N_0$ )

Epsilon-produk dan keleluasaan ruang-waktu

Semua hal di atas mengarah ke pertanyaan mendasar: a bukan multiplikasi epsilon-multiplikasi "benar" di dunia fisik kita (setidaknya dalam hal ruang atau waktu)?

Pertimbangkan, misalnya, persamaan Schrödinger satu dimensi:

$i\hbar\frac{\partial}{\partial t}\Psi(x,t)=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\Psi(x,t) + U(x,t)\Psi(x,t)$

Persamaan ini mengasumsikan kontinuitas ruang-waktu dan kemungkinan nilai yang sangat kecil

$\Delta x$ dan

$\Delta t$ (ini diterima secara implisit jika kita menggunakan diferensiasi). Jika kita berbicara tentang waktu, ini menyiratkan energi tanpa batas, yang bertentangan dengan ide-ide modern tentang alam semesta.

Agar tidak menyulitkan argumen, mari kita pertimbangkan kasusnya kapan

$U$ independen dari

$t$ . Pada kasus ini

$\Psi(x,t)$ dapat ditulis sebagai:

$\Psi(x,t) = \psi(x)\exp(-iEt/\hbar)$

Tapi

$\exp(-iEt/\hbar)$ Adalah fungsi analitik, yang berarti kita dapat menerapkan pendekatan kita untuk itu, yaitu, kita dapat membuat transformasi epsilon (relatif terhadap waktu) dari persamaan Schrödinger asli kami dan kami mendapatkan

$i\hbar\overset{\displaystyle\epsilon}{\nabla}\overset{\displaystyle\epsilon}\Psi(x,t)=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\overset{\displaystyle\epsilon}\Psi(x,t) + U(x)\overset{\displaystyle\epsilon}\Psi(x,t)$

$\overset{\displaystyle\epsilon}\Psi(x,t) = \psi(x)\epsilon exp(-iEt/\hbar)$

Di mana

$\overset{\displaystyle\epsilon}\Psi(x,t) \overset{\epsilon \to 0}{\to}\Psi(x,t)$

Yaitu, dengan langkah waktu yang sangat kecil (time quantum)

$\epsilon$ yang tidak penting untuk perhitungan kita, kita tidak akan melihat perbedaan antara solusi dari persamaan Schrödinger (biasa) dan solusi dari persamaan epsilon-Schrödinger.

Tetapi kemudian ini berarti bahwa kita tidak dapat benar-benar mengatakan karya mana yang "benar" ("digunakan" secara alami) - produk biasa atau epsilon kami (dengan kuantisasi waktu yang cukup kecil).

Selain itu, dalam kasus produk epsilon (dan, karenanya, persamaan Schrödinger epsilon dan solusi gelombang epsilon), kami memiliki kuantisasi waktu plus yang jelas menjadi alami, dan kami tidak menemukan kebutuhan energi tak terbatas. Sebenarnya, kita memiliki persamaan yang sama dengan solusi yang sama, tetapi pada saat yang sama kita secara alami menghilangkan kebutuhan akan asumsi kesinambungan waktu.

- , , , , . , . , , $\Delta x \ll \delta_x$ / $\Delta t \ll \delta_t$ . , , . « » , $\Delta x \gg \delta_x$ / $\Delta t \gg \delta_t$ . , . -, , $\epsilon$ — $\Delta x$ / $\Delta t$ ketika masih masuk akal untuk berbicara tentang waktu dan / atau ruang (berbicara kasar, ini adalah ukuran rata-rata "tempat").

Bagaimana cara mengeceknya?

Jadi, jika waktu terpisah dengan "langkah"

$\epsilon$ , dan penggandaan “benar” adalah penggandaan epsilon dengan kelangkaan waktu, lalu bagaimana ini bisa diwujudkan? Apakah mungkin untuk membuat pemikiran atau percobaan nyata dan memahami karya mana yang "benar" dan langkah (kuantum) mana yang digunakan?

Beberapa perkiraan dapat diberikan untuk memahami seberapa besar ide-ide kita tentang dunia akan berubah jika "epsilon-multiplikasi" (daripada multiplikasi biasa) akan "benar".

Ingat itu

$\epsilon{exp(i\omega_0 t)}_{\frac{t}{\epsilon}}=\left({{1+\omega_0^2 \epsilon^2}}\right)^{\frac{t}{2\epsilon}}\exp{(i \displaystyle \frac{arctg(\omega_0 \epsilon)}{ \epsilon}t)}$

Lalu untuk

$\omega_0\epsilon \ll 1$ kita punya:

frekuensi akan berbeda dari frekuensi gelombang sinus $\omega_0$ dan akan sama

$\omega = \displaystyle \frac{arctg(\omega_0 \epsilon)}{ \epsilon} \approx \omega_0(1 - \displaystyle\frac{\omega_0^2\epsilon^2}{3})$
amplitudo akan meningkat sebagai

$(1+(\omega_0\epsilon)^2))^{\frac{t}{2\epsilon}} \approx 1 + \displaystyle\frac{t\omega^2_0\epsilon}{2}$

Mari kita secara kasar menilai apakah kita dapat melihat perbedaan ini?

Contoh 1. Perubahan selama kehidupan alam semesta.

Misalkan kelonggaran duniawi kita sebanding dengan waktu Planck:

$t_p \approx 10^{−43 }$ detik

Seumur hidup semesta:

$t_{u} \approx 10^{17}$ detik

Cari frekuensi apa

$\omega_0$ selama masa alam semesta, amplitudo osilasi dapat berubah, misalnya, sebesar 0,5%.

$t_u t_p\omega^2_0 = 10^{-2}$

$\omega_0 = \displaystyle\frac{10^{-1}}{\sqrt{t_ut_p}} = 10^{-1}10^{13} = 10^{12}$ rad / s

Ini berarti bahwa untuk frekuensi urutan 1 THz (atau untuk partikel dengan energi)

$10^6$ eV) selama masa semesta, amplitudo (fungsi gelombang) akan berubah sekitar satu persen (urutan). Yaitu, jelas bahwa setidaknya dalam kehidupan biasa kita tidak bisa melihatnya sama sekali.

Contoh 2. Perubahan per detik

Mari kita perkirakan berapa kali amplitudo dari fungsi gelombang suatu partikel berenergi sangat tinggi

$10^{18}$ eV dalam satu detik.

$10^{18}$ ev sesuai dengan urutan

$10^{24}$ Hz

$(1+(\omega_0 t_p)^2))^{\frac{1}{2t_p}} \approx 10^{48}10^{-43} = 10 ^5$

Artinya, dalam satu detik amplitudo fungsi gelombang dari partikel semacam itu akan meningkat 100 ribu kali (urutan).

Itu terlihat substansial. Tapi bagaimana cara mendeteksinya? Faktanya adalah bahwa makna fisik tidak memiliki fungsi gelombang itu sendiri, tetapi

$\Psi\Psi^*$ , dan dalam hal epsilon-image itu akan menjadi

$\overset{\epsilon}\Psi \displaystyle\overset{\displaystyle \epsilon}{*}\overset{\epsilon}\Psi$ . Tapi

$\epsilon exp(-iEt/\hbar) \overset{\displaystyle\epsilon}{*} \epsilon exp(iEt/\hbar) = 1$

Ini menunjukkan bahwa hanya kuantitas yang memiliki makna fisik tidak akan berubah, dan pendekatan ini tidak akan memungkinkan kita untuk menjawab pertanyaan yang diajukan.

Jawaban atas pertanyaan dari komentar

Bagaimana produk epsilon diperoleh?

( 0).
:

$f(x)g(x) = exp(\nabla_f + \nabla_g) f(x)g(x)|_{x=0}$

$exp(\nabla_f + \nabla_g)$ —

$1 + (\nabla_f + \nabla_g) + (\nabla_f + \nabla_g)^2/2! + (\nabla_f + \nabla_g)^3/3! + ...$

,

$exp(ax) = \lim\limits_{\epsilon \rightarrow 0,k\epsilon = x}(1+a\epsilon)^k$

-,

$exp (ax)$

$(1+a\epsilon)^k$ ( , -) ,

$f(x), g(x)$ (

$A^ \epsilon$ )

$f_n, g_n$ .

, , :

$\overset{\wedge}{I}$ — :

$\overset{\wedge}{I} f_n = f_n$

,

$p_k = (f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=f_0g_0+C_k^1\epsilon({f\overset{\displaystyle\epsilon}{'}}|_0g_0+{g\overset{\displaystyle\epsilon}{'}}|_0f_0)+C_k^2\epsilon^2({f^{\overset{\displaystyle\epsilon}{(2)}}}|_0g_0+2{f\overset{\displaystyle\epsilon}{'}}|_0{g\overset{\displaystyle\epsilon}{'}}|_0+{g^{\overset{\displaystyle\epsilon}{(2)}}}|_0f_0)+\ldots$

:

$p_k = (f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=\sum_{j=0}^{k}C_{k}^{j}\epsilon^j\sum_{i=0}^{j}C_{j}^{i}{f^{\overset{\displaystyle\epsilon}{(i)}}}|_0{g^{\overset{\displaystyle\epsilon}{(j-i)}}}|_0$

:

$p_k=(f\displaystyle\overset{\displaystyle\epsilon}{*}{g})_k=\sum_{j+i+l=k}C_k^{j,i}f_ig_j(-1)^{l}$

$C_{k}^{j,i}$ — :

$C_{k}^{j,i}=\displaystyle\frac{k!}{j!i!l!}$ , (

$l+j+i=k$ )

Persamaan diferensial nonlinier, diskresi ruang-waktu dan produk epsilon

Ringkasan

Fungsi kisi dan turunan epsilon

Penggandaan Epsilon

Konversi Epsilon

Transformasi Epsilon untuk Rumus Trigonometrik

Contoh pemecahan persamaan diferensial dengan metode pemetaan epsilon

Properti pemetaan Epsilon sebagai ε → 0

Fungsi non analitik

Epsilon-produk dan keleluasaan ruang-waktu

Bagaimana cara mengeceknya?

Jawaban atas pertanyaan dari komentar

More articles: