☄️ 👨🏾‍🎤 🎌 Julia dan automata seluler 🌴 😑 🕐

Hari ini kita akan melakukan perjalanan yang penuh warna melalui dunia automata seluler, secara simultan mempelajari beberapa trik penerapannya, dan juga mencoba untuk memahami apa yang tersembunyi di balik keindahan ini - permainan penasaran untuk pikiran kosong atau konsep filosofis yang mendalam yang beresonansi dengan banyak model.

Untuk latihan dan pemahaman yang lebih baik, Anda harus mencoba menerapkan algoritme berikut sendiri. Nah, jika malas, atau hanya karena ketertarikan, Anda bisa bermain-main dengan berbagai implementasi:

Golly — . .
Lenia — "".
. ,

— . , 0 1, , . . , . , . , 256 ( 8- ).

, .

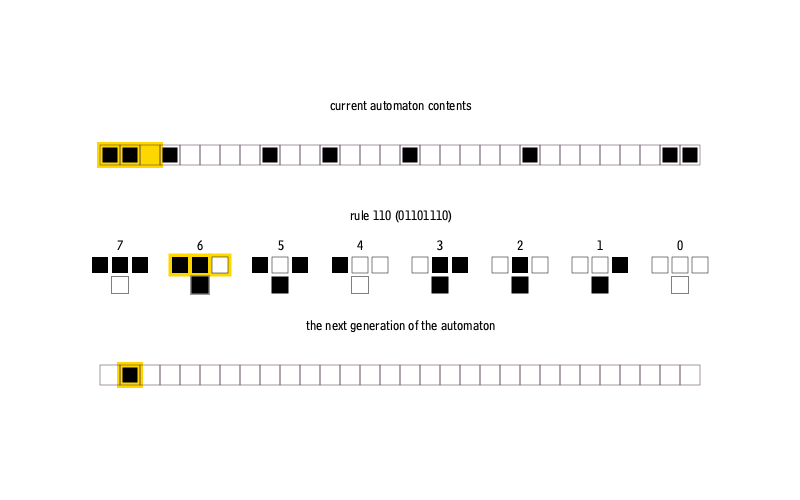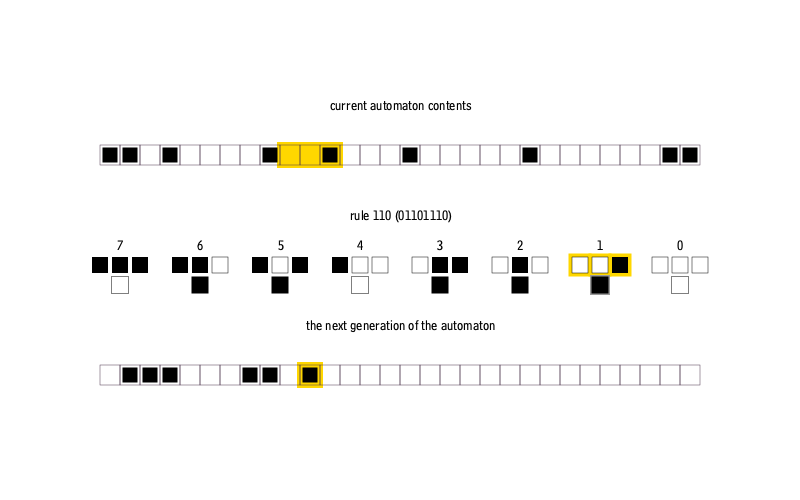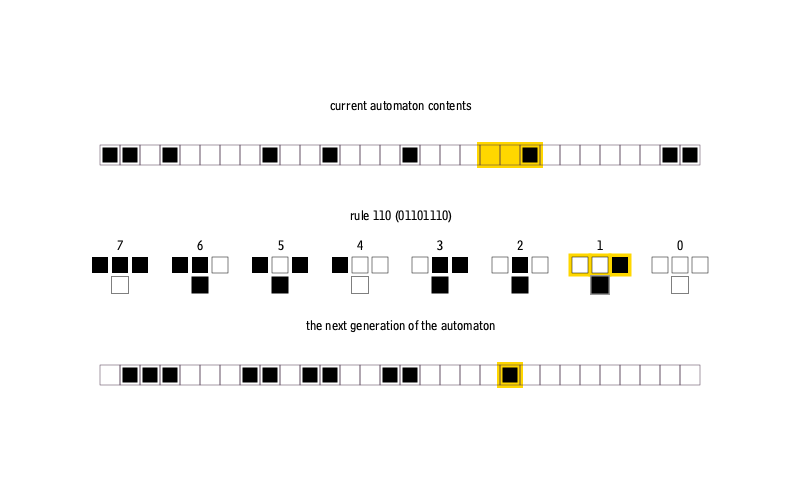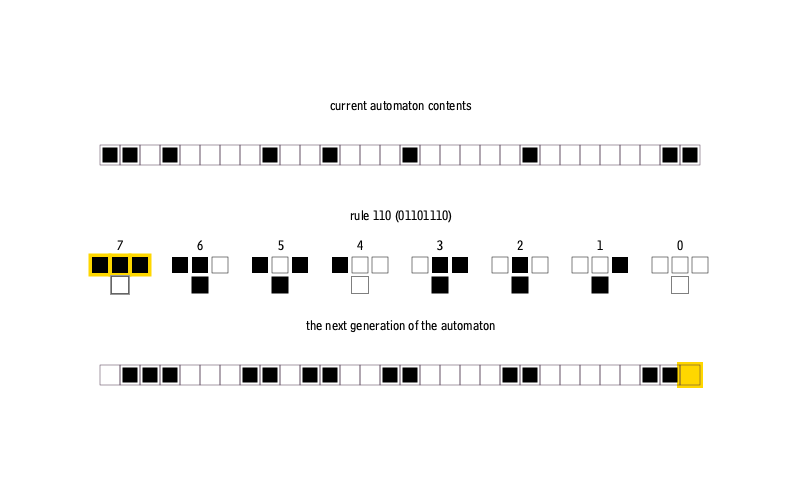
using Pkg
pkgs = ["Images", "ColorSchemes", "FFTW"]

for p in pkgs
    Pkg.add(p)
end

using Images, ColorSchemes, FFTW, LinearAlgebra: kron
using Random: bitrand
cd("C:\\Users\\User\\Desktop\\Mycop")

0 255 ( ). , . , , :

# , ,    
function cellauto( n::Int64, m::Int64, rule::Int64, s::Int64 = 1 )

    ptrn = digits(Bool, rule, base = 2, pad = 8)
    bt = [ bitstring(i)[end-2:end] for i = 0:7 ]
    d = Dict( bt[i] => ptrn[i] for i = 1:8 ) # 

    M = falses(n,m)
    M[1,m ÷ 2] = true
    #M[1,:] .= bitrand(m)
    for i = 1:n-1, j = 2:m-1
        key = "$(M[i, j-1]*1)$(M[i, j]*1)$(M[i, j+1]*1)"
        M[i+1,j] = d[key]
    end
    kron(M, ones(Int,s,s) ) #  
end

M0 = cellauto(100, 200, 30, 4)
Gray.( M0 )

30, . , , . , - : , … , . :

Arr = cellauto.(40, 40, [0:23;], 2);
Imgs = [ Gray.(a) for a in Arr ]
reshape(Imgs, 4,6)

, . :

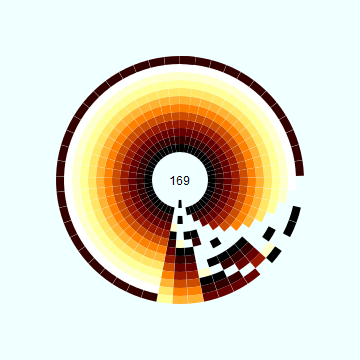
Luxor, .

"" — ( ) . , , : , ( ) .

: , , ( !) . , , , . . . , , , , , , . "" .

, , . , , .

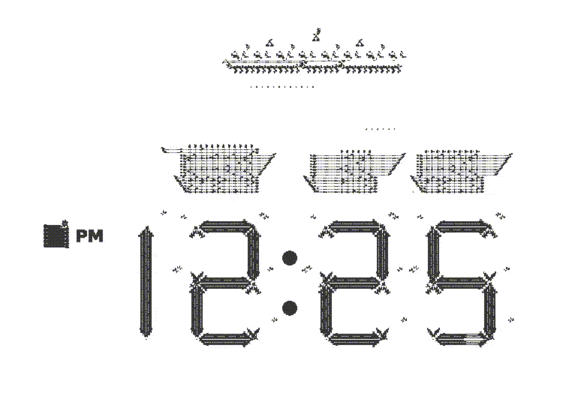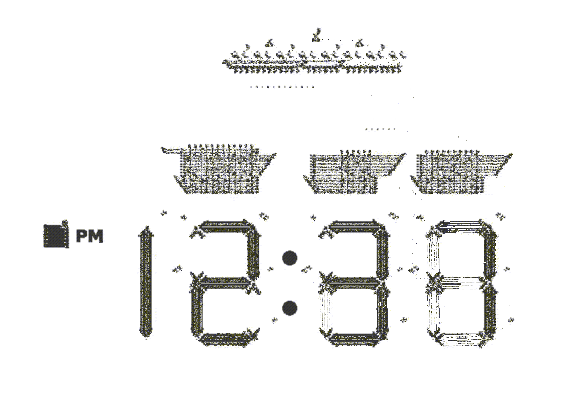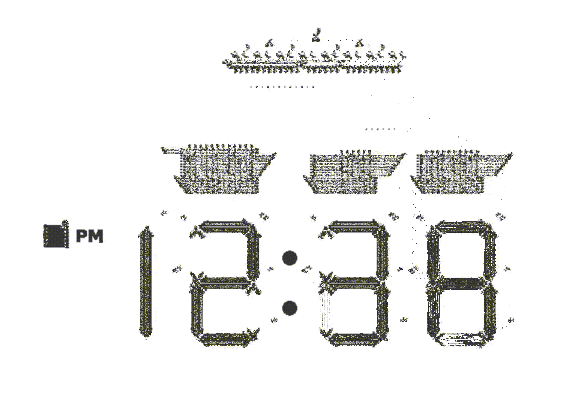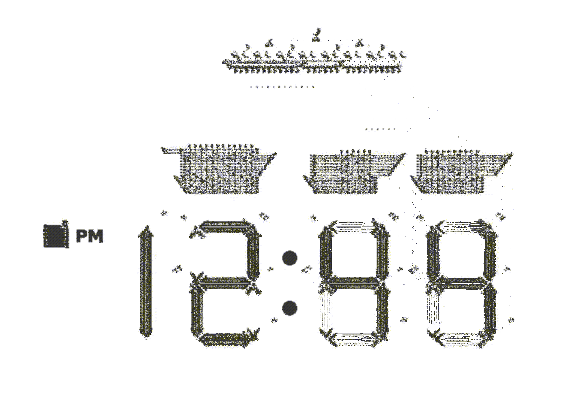
function makefilter(N::Int64)
    filter = zeros(Complex, N, N);
    IDX(x, y) = ( (x + N) % N ) + ( (y+N) % N ) * N + 1
        filter[IDX(-1, -1)] = 1. ;
        filter[IDX( 0, -1)] = 1. ;
        filter[IDX( 1, -1)] = 1. ;
        filter[IDX(-1,  0)] = 1. ;
        filter[IDX( 1,  0)] = 1. ;
        filter[IDX(-1,  1)] = 1. ;
        filter[IDX( 0,  1)] = 1. ;
        filter[IDX( 1,  1)] = 1. ;

    return fft( real.(filter) )
end

function fftlife(N = 16, steps = 100, dx = 0, glider = true)

    if glider
        state = falses(N, N)
        state[4,5] = state[5,6] = state[6,6] = true
        state[6,5] = state[6,4] = true
    else
        state = bitrand(N, N)
    end

    filter = makefilter(N)

    for i in 1:steps
        tmp = fft( real.(state) ) # forward
        tmp .*= filter

        summ = ifft(tmp) # reverse

        for i in eachindex(state)
            t = round( Int, real(summ[i]) ) >> dx
            state[i] = ( state[i] ? t == 2 || t == 3 : t == 3 )
        end
        save("KonLife_$(N)x$(N)_$i.png", kron( Gray.(state), ones(8,8) ) )
    end

end

fftlife(16, 60)

— , ( ). , "" .

\frac{d f (x, t)}{d t} = S (N (x, t), M (x, t)) - f (x, t) S (n, m) = σ_{n} (σ_{m} (b_{1}, b_{2}), σ_{m} (d_{1}, d_{2})) M (x, t) = \frac{1}{π h^{2}} \int_{0 \leq | y | \leq h} f (x - y, t) d y N (x, t) = \frac{1}{8 π h^{2}} \int_{0 \leq | y | \leq 3 h} f (x - y, t) d y

$\frac{df(x,t)}{dt} = S\left(N(x,t),M(x,t) \right ) - f(x,t) \\ \\ S(n,m) = \sigma_n\left(\sigma_m(b_1, b_2), \sigma_m(d_1,d_2)\right)\\ M(x,t) = \frac{1}{\pi h^2} \int\limits_{0\le |y| \le h} f(x-y, t) dy \\ N(x,t) = \frac{1}{8\pi h^2} \int\limits_{0\le |y| \le 3h} f(x-y, t) dy$

1 0, , , .

Kondisi awal

function clamp(x)
    y = copy(x)
    y[x.>1] .= 1
    y[x.<0] .= 0
    y
end

function func_linear(X, a, b)
    Y = [ (x-a + 0.5b)/b for x in X ]

    Y[X.<a-0.5b] .= 0
    Y[X.>a+0.5b] .= 1
    return Y
end

function splat!(aa, ny, nx, ra)
    x = round(Int, rand()*nx ) + 1
    y = round(Int, rand()*ny ) + 1
    c = rand() > 0.5

    for dx = -ra:ra, dy = -ra:ra
        ix = x+dx
        iy = y+dy
        if ix>=1 && ix<=nx && iy>=1 && iy<=ny
            aa[iy,ix] = c
        end
    end
end

function initaa(ny, nx, ra)
    aa = zeros(ny, nx)
    for t in 0:((nx/ra)*(ny/ra))
        splat!(aa, ny, nx, ra);
    end
    aa
end

Sigmoid

func_smooth(x::Float64, a, b)  = 1 / ( 1 + exp(-4(x-a)/b) ) 

sigmoid_a(x, a, ea) = func_smooth(x, a, ea)
sigmoid_b(x, b, eb) = 1 - sigmoid_a(x, b, eb)
sigmoid_ab(x, a, b, ea, eb) = sigmoid_a(x, a, ea) * sigmoid_b(x, b, eb)
sigmoid_mix(x, y, m, em) = x - x * func_smooth(m, 0.5, em) + y * func_smooth(m, 0.5, em)

function snm(N, M, en, em, b1, b2, d1, d2)

    [ sigmoid_mix( sigmoid_ab(N[i,j], b1, b2, en, en), 
                   sigmoid_ab(N[i,j], d1, d2, en, en), M[i,j], em ) 
                    for i = 1:size(N, 1), j = 1:size(N, 2) ]
end

Fungsi utama

function smoothlife(NX = 128, NY = 128, tfin = 10, scheme = 1)

    function derivative(aa)
        aaf = fft(aa)
        nf = aaf .* krf
        mf = aaf .* kdf
        n = real.(ifft(nf)) / kflr # irfft
        m = real.(ifft(mf)) / kfld
        2snm(n, m, alphan, alpham, b1, b2, d1, d2) .- 1
    end

    ra = 10
    ri = ra/3
    b = 1
    b1 = 0.257
    b2 = 0.336
    d1 = 0.365
    d2 = 0.551
    alphan = 0.028
    alpham = 0.147

    kd = zeros(NY,NX)
    kr = zeros(NY,NX)
    aa = zeros(NY,NX)

    x = [ j - 1 - NX/2 for i=1:NY, j=1:NX ]
    y = [ i - 1 - NY/2 for i=1:NY, j=1:NX ]

    r = sqrt.(x.^2 + y.^2)
    kd = 1 .- func_linear(r, ri, b) # ones(NY, NX)
    kr = func_linear(r, ri, b) .* ( 1 .- func_linear(r, ra, b) )
    #aa = snm (ix/NX, iy/NY, alphan, alpham, b1, b2, d1, d2);
    kflr = sum(kr)
    kfld = sum(kd)
    krf = fft(fftshift(kr))
    kdf = fft(fftshift(kd))

    #for td in 2 .^(10:-1:3)
    for td = 64

        aa = initaa(NY,NX,ra)
        dt = 1/td;
        l = 0
        nx = 0
        for t = 0:dt:tfin
# 1=euler  2=improved euler  3=adams bashforth 3  4=runge kutta 4
            if scheme==1

                aa += dt*derivative(aa)

            elseif scheme==2

                da = derivative(aa);
                aa1 = clamp(aa + dt*da)
                for h = 0:20
                    alt = aa1
                    aa1 = clamp(aa + dt*(da + derivative(aa1))/2)
                    if maximum(abs.(alt-aa1))<1e-8 
                        break
                    end
                end
                aa = copy(aa1)

            elseif scheme==3

                n0 = 1+mod(l,3)
                n1 = 1+mod(l-1,3)
                n2 = 1+mod(l-2,3)

                f = zeros(NY, NX, 3) # ?
                f[:,:,n0] = derivative(aa)
                if l==0
                    aa += dt*f[:,:,n0]
                elseif l==1
                    aa += dt*(3*f[:,:,n0] - f[:,:,n1])/2
                elseif l>=2
                    aa += dt*(23*f[:,:,n0] - 16*f[:,:,n1] + 5*f[:,:,n2])/12
                end

            elseif scheme==4

                k1 = derivative(aa)
                k2 = derivative(clamp(aa + dt/2*k1))
                k3 = derivative(clamp(aa + dt/2*k2))
                k4 = derivative(clamp(aa + dt*k3))
                aa += dt*(k1 + 2*k2 + 2*k3 + k4)/6

            end

            aa = clamp(aa)

            if t >= nx
                save("$(scheme)\\$(td)_$t.png", Gray.(kron(aa, ones(2, 2) ) ) )
                nx += 1;
            end

            l += 1;
        end

    end     # for td
end

@time smoothlife(256, 256, 20, 3)

, . , . .

— , , . — .

, , , :

— $90^\circ$ , , .
— $90^\circ$ , , .

rosetta code , :

function ant(width, height)
    y, x = fld(height, 2), fld(width, 2)
    M = trues(height, width)

    dir = im
    for i in 0:1000000
        x in 1:width && y in 1:height || break
        dir *= M[y, x] ? im : -im
        M[y, x] = !M[y, x]
        x, y = reim(x + im * y + dir)
        i%100==0 && save("LR//zLR_$i.png", Gray.( kron(M,ones(4,4) ) ) )
    end

    Gray.(M)
end

ant(100, 100)

, . — . !

function ant(width, height, comnds;
        steps = 10, cxema = reverse(ColorSchemes.hot), 
        savevery = 100, pixfactor = 20)

    ma3x2pix() = [ clrs[k%n+1] for k in M ]
      bigpix() = kron( ma3x2pix(), ones(Int64,m,m) )
    save2pix(i) = save("$(comnds)_$i.png", bigpix() )

    m = pixfactor
    n = length(comnds)
    colorsinscheme = length(cxema)
    M = zeros(Int64, height, width)
    y, x = fld(height, 2), fld(width, 2)

    st = colorsinscheme ÷ n
    clrs = [ cxema.colors[i] for i in 1:st:colorsinscheme ]

    dir = im
    for i in 0:steps
        x in 1:width && y in 1:height || (save2pix(i); break)
        j = M[y, x] % n + 1
        dir *= comnds[j] == 'L' ? -im : im
        M[y, x] += 1
        x, y = reim(x + im * y + dir)

        i % savevery==0 && save2pix(i)
    end
    ma3x2pix()
end

@time ant(16, 16, "LLRR", steps = 100, savevery = 1, pixfactor = 20)

, !

LLRR

. , ? ?..

# http://rosettacode.org/wiki/Mandelbrot_set
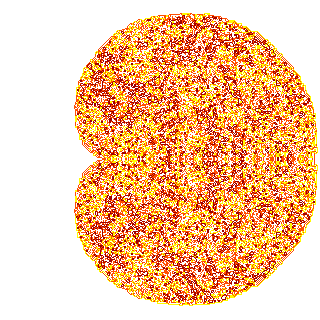
function hsv2rgb(h, s, v)
    c = v * s
    x = c * (1 - abs(((h/60) % 2) - 1) )
    m = v - c

    r,g,b =
        if h < 60
            (c, x, 0)
        elseif h < 120
            (x, c, 0)
        elseif h < 180
            (0, c, x)
        elseif h < 240
            (0, x, c)
        elseif h < 300
            (x, 0, c)
        else
            (c, 0, x)
        end

    (r + m), (b + m), (g + m)
end

function mandelbrot()

    w, h = 1000, 1000

    zoom  = 1.0
    moveX = 0
    moveY = 0

    img = Array{RGB{Float64}, 2}(undef,h, w)
    maxIter = 30

    for x in 1:w
        for y in 1:h
            i = maxIter
            c = Complex(
                (2*x - w) / (w * zoom) + moveX,
                (2*y - h) / (h * zoom) + moveY
            )
            z = c
            while abs(z) < 2 && (i -= 1) > 0
                z = z^2 + c
            end
            r,g,b = hsv2rgb(i / maxIter * 360, 1, i / maxIter)
            img[y,x] = RGB{Float64}(r, g, b)
        end
    end

    save("mandelbrot_set2.png", img)
end

mandelbrot()

RRRLRRLRRR

RRRLR9000000

RRLRLLRRRRLL

RRLR

RRLLLRLRL

RRLLLRLLLRLL

RRLLLRLLLLL_200000000

— . :

RRLLLL30_000_299_000

Rllr

RLLLLRRRLLL

RLLLLLLLRRL

LLRLLLL

, . (-), -, , , ! , !

. ,

, . ( - . )

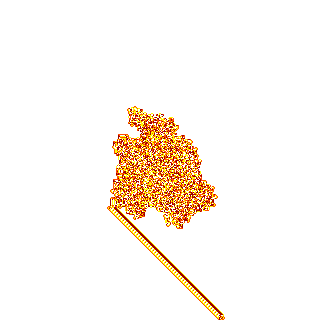
Topik automata seluler dengan pertumbuhan daya komputasi dan peningkatan algoritma menjadi lebih populer. Blog Wolfram memiliki laporan kecil tentang topik ini, dan semua orang dapat melihatnya sendiri - ada banyak artikel, yang paling bervariasi: ada pertemanan dengan jaringan saraf, generator angka acak, titik kuantum, kompresi, dan banyak lagi ...

Dan akhirnya, struktur penyalinan-diri yang dibuat oleh Ted Codd untuk meminta satu liter bir

Julia dan automata seluler

More articles: