🌅 🤡 🧚🏻 Visualisasi garis-garis ketegangan dan gerakan muatan elektrostatik, simulasi gerakan planet tata surya 🧜🏼 😛 🐨

Hai, hari ini saya ingin menawarkan bantuan visual untuk memodelkan beberapa proses fisik dan menunjukkan cara mendapatkan gambar dan animasi yang indah. Perhatian banyak gambar.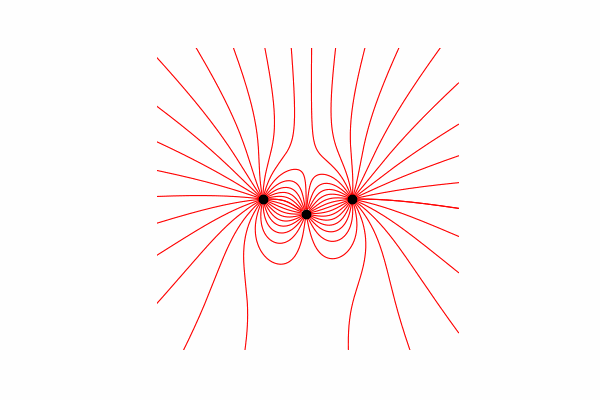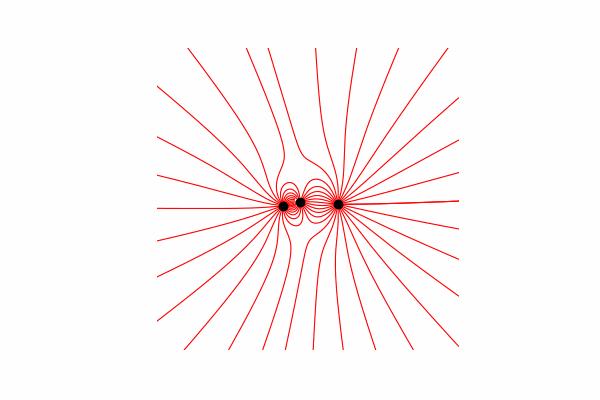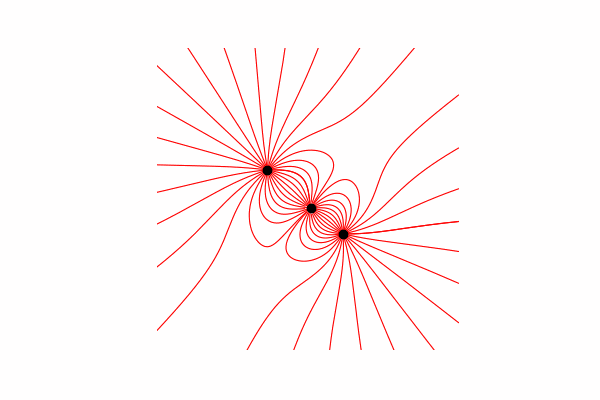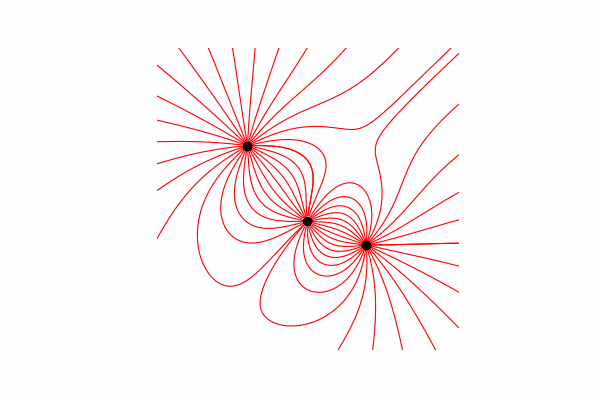

Semua kode dapat ditemukan di google colab .

Teori

Pertama, kita membutuhkan teori minimum untuk topik ini. Mari kita mulai dengan memahami apa garis ketegangan dan bagaimana cara menghitungnya. Sebenarnya, garis-garis ini adalah penggabungan dari banyak vektor tegangan, yang dapat dihitung sebagai berikut: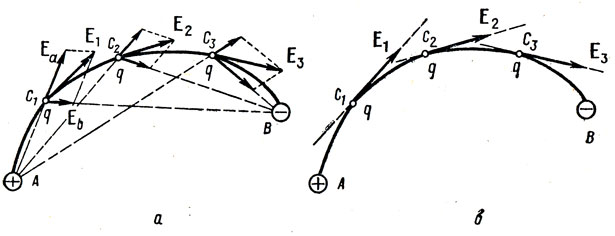

E = \frac{k * | q |}{r^{2}}

$E=\frac{k*|q|}{r^2}$

gambar

Metode perhitungan E

Saya menghitung vektor tegangan melalui kesamaan segitiga, dengan demikian memperoleh proyeksi pada sumbu x dan y masing-masing dx dan dy.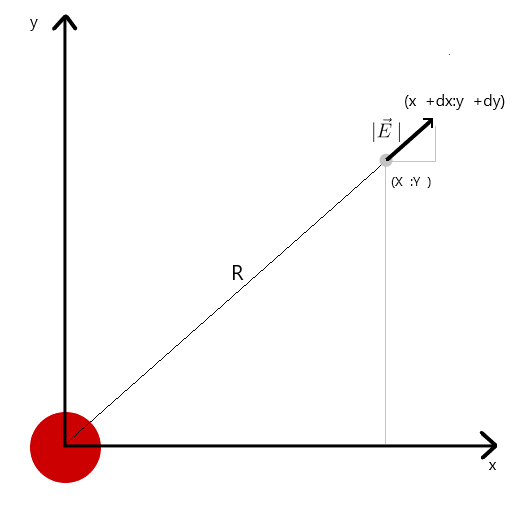

Dari kemiripan ini mengikuti bahwa jari-jari vektor dari muatan ke titik dalam ruang r dan panjang vektor intensitas E sama dengan rasio proyeksi vektor-vektor ini (masing-masing x1 dan dx)

. Formula vektor yang dihasilkan

\frac{R}{E} = \frac{x}{d x} = \frac{y}{d y}

$\frac{R}{E}=\frac{x}{dx}=\frac{y}{dy}$

\vec{E} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{E}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{E}}_{i} |}{R_{i}} \end{matrix})

$\vec{E}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{E}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{E}_i|}{R_i} \end{array}\right) \qquad$
dengan pengetahuan ini kita mendapatkan hasil pertama.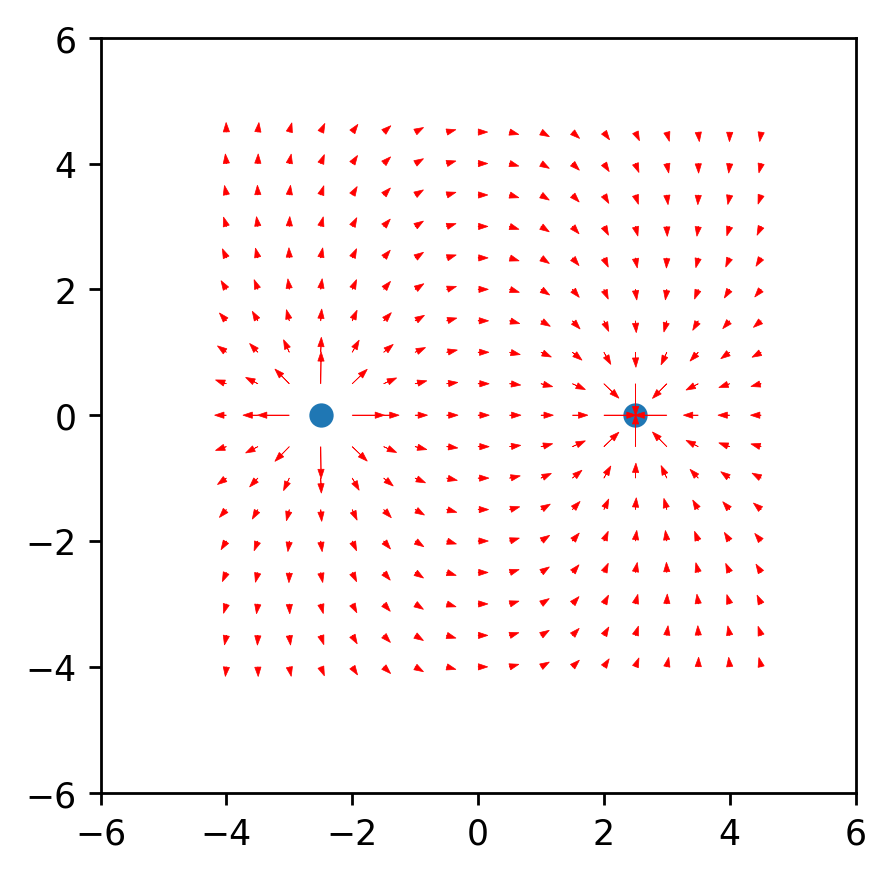

Fungsi Perhitungan Proyeksi

def E(q_prop, xs, ys, nq): #q_prop=[[xq1, yq1, q1, mq1, vxq1, vyq1], [xq2, yq2, q2, mq2, vxq2, vyq2] ... ] 
    l=1
    k=9*10**9
    Ex=0
    Ey=0
    c=0
    for c in range(len(q_prop)):#                
        q=q_prop[c]
        r=((xs-q[0])**2+(ys-q[1])**2)**0.5
        dEv=(k*q[2])/r**2
        dEx=(xs-q[0])*(dEv/r)*l
        dEy=(ys-q[1])*(dEv/r)*l

        Ex+=dEx
        Ey+=dEy
    return Ex, Ey

Metode konstruksi garis

Pertama, Anda perlu memutuskan titik awal dan akhir dari mana garis dan dokumen akan pergi. Awal adalah titik pada lingkaran dengan jari-jari r di sekitar muatan, dan titik akhir tidak lebih dari r terpisah dari muatan.

kode untuk titik awal

theta = np.linspace(0, 2*np.pi, n)
mask=q_prop[ q_prop[:,2]>0 ]#    
for cq in range(len(mask)):
    qmask=mask[cq]
    xr = r_q*np.cos(theta)+qmask[0]# -    
    yr = r_q*np.sin(theta)+qmask[1]#

Jadi pantas dikatakan bahwa saluran hanya dibangun dari muatan positif.

Dan akhirnya, konstruksi garis. Untuk melakukan ini, kami membuat garis vektor tegangan di dalamnya dari titik awal, memperbarui titik awal di akhir garis yang dibuat dan mengulangi hingga kondisi akhir yang disebutkan di atas tercapai.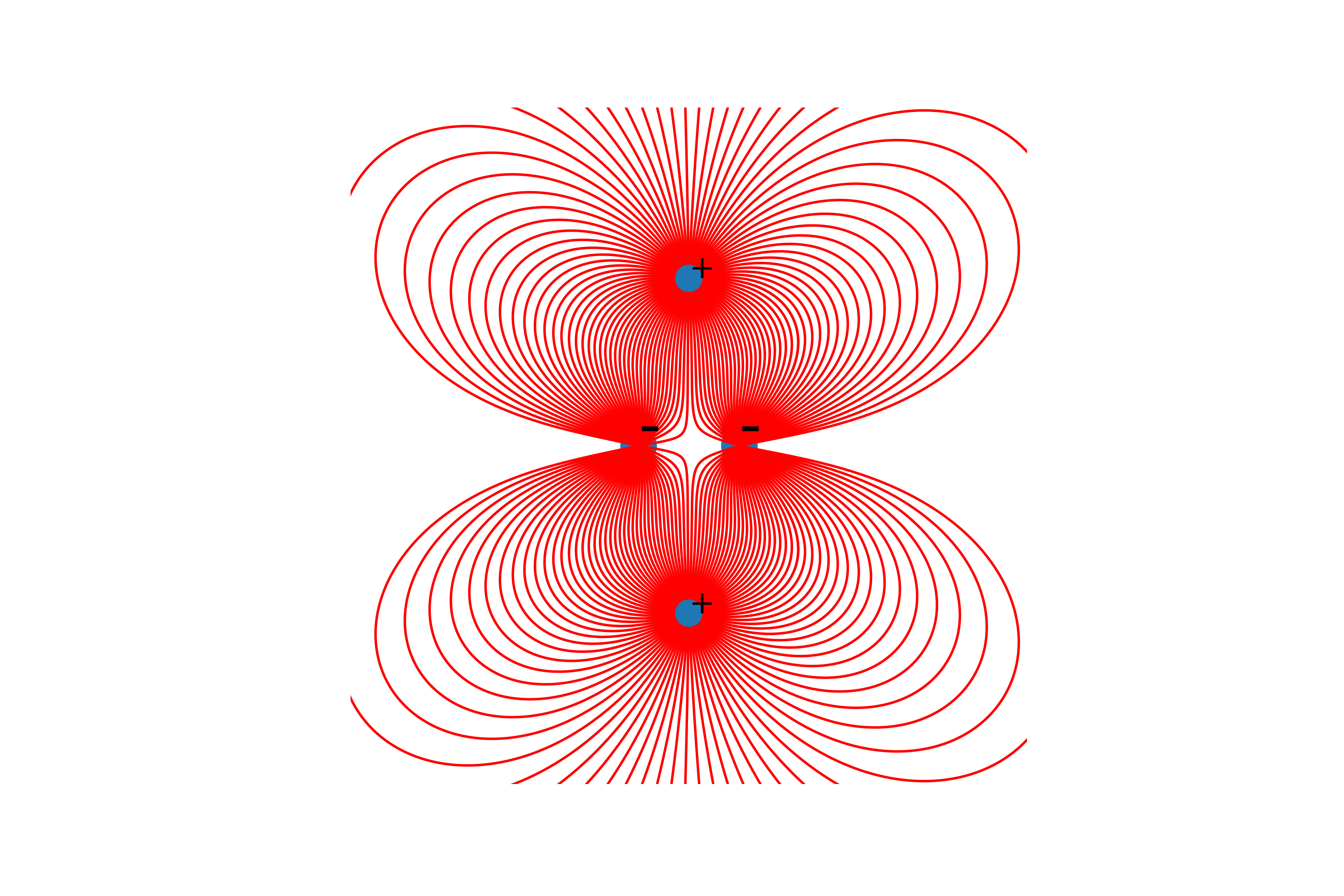

fungsi perhitungan koordinat garis

def Draw(size, q_prop,r_q, n):
  
  linen=np.empty((np.count_nonzero(q_prop[:,2]>0),n, 2000000), dtype=np.float64)
  linen[:] = np.nan
  theta = np.linspace(0, 2*np.pi, n)
  mask=q_prop[ q_prop[:,2]>0 ][ q_prop[q_prop[:,2]>0][:,3]==1 ]
  for cq in range(len(mask)):
    qmask=mask[cq]
    x11 = r_q*np.cos(theta)+qmask[0]
    x22 = r_q*np.sin(theta)+qmask[1]
    for c in range(len(x11)):

      xs=x11[c]
      ys=x22[c]

      lines=np.empty((2,1000000), dtype=np.float64)
      lines[:]=np.nan
      stop=0
      nnn=0
      
      lines[0][nnn]=xs
      lines[1][nnn]=ys
      while  abs(xs)<size+2 and abs(ys)<size+2: 
        nnn+=1

        for cq1 in range(len(q_prop)):
          q=q_prop[cq1]
          if ((ys-q[1])**2+(xs-q[0])**2)**0.5<r_q/2 :
            stop=1
            break
        if stop==1:
          break
        dx, dy = E1(q_prop,xs,ys)

        xs+=dx
        ys+=dy
        lines[0][nnn]=xs
        lines[1][nnn]=ys
       
      linen[cq,c,:]=lines.reshape(-1)

  return linen

Interaksi antar biaya

Untuk mencerminkan interaksi mereka, perlu untuk mengubah koordinat dan kecepatan setelah setiap waktu kecil.

x + = \frac{E_{x} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{x} \cdot d t

$x+=\frac{E_x \cdot q \cdot dt^2}{2\cdot m} + v_x\cdot dt$

y + = \frac{E_{y} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{y} \cdot d t

$y+=\frac{E_y \cdot q \cdot dt^2}{2\cdot m} + v_y \cdot dt$

v_{x} + = \frac{E_{x} \cdot q \cdot d t}{m}

$v_x+= \frac{E_x \cdot q \cdot dt}{ m}$

v_{y} + = \frac{E_{y} \cdot q \cdot d t}{m}

$v_y+= \frac{E_y \cdot q \cdot dt}{ m}$

Berfungsi untuk memperbarui koordinat dan proyeksi kecepatan pengisian daya

def Update_all(q_prop):
  vx=0
  vy=0
  x=0
  y=0
  q_prop_1=np.copy(q_prop)
  for c in range(len(q_prop)):#         
    xs=q_prop[c][0]
    ys=q_prop[c][1]
    q =q_prop[c][2]
    m =q_prop[c][3]
    vx=q_prop[c][4]
    vy=q_prop[c][5]
    Ex, Ey= E(q_prop, xs, ys, c)

    x=(((Ex*q)/m)*dt**2)/2+vx*dt+xs
    y=(((Ey*q)/m)*dt**2)/2+vy*dt+ys
    vx+=((Ex*q)/m)*dt
    vy+=((Ey*q)/m)*dt
    #print(q_prop[c]-[x,y,q,m,vx,vy])
    q_prop_1[c]=[x,y,q,m,vx,vy]
  
  return q_prop_1#

Gravitasi

Berdasarkan kode yang ada, saya menulis sebuah simulator yang mencerminkan gerakan tubuh di bawah pengaruh gravitasi. Perubahan dalam kode terutama untuk fungsi ketegangan sejak itu akselerasi sekarang akan dianggap menggunakan formula yang sama.

g = \frac{G * m}{r^{2}}

$g=\frac{G*m}{r^2}$

\vec{g} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{g}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{g}}_{i} |}{R_{i}} \end{matrix})

$\vec{g}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{g}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{g}_i|}{R_i} \end{array}\right) \qquad$

Planet mulai dari sumbu x pada jarak perihelion dan pada kecepatan perihelion. Semua nilai planet dan matahari (massa, jarak, ekstremitas) dari direktori.

Animasi untuk 4 planet pertama + matahari.

Menunggu kritik dan saran. Sampai jumpa.

Visualisasi garis-garis ketegangan dan gerakan muatan elektrostatik, simulasi gerakan planet tata surya

Teori

Metode perhitungan E

Metode konstruksi garis

Interaksi antar biaya

Gravitasi

More articles: