Orang-orang bertemu dengan sistem pemberi rekomendasi. Faktorisasi

Pembelajaran mesin telah cukup merambah kehidupan kita sehari-hari. Beberapa tidak lagi terkejut ketika mereka diberitahu tentang jaringan saraf di smartphone mereka. Salah satu bidang besar dalam ilmu ini adalah sistem rekomendasi. Mereka ada di mana-mana: ketika Anda mendengarkan musik, membaca buku, menonton acara TV atau video. Perkembangan ilmu ini terjadi di perusahaan raksasa seperti YouTube , Spotify dan Netfilx . Tentu saja, semua prestasi ilmiah di bidang ini diterbitkan baik di konferensi NeurIPS atau ICML yang terkenal , dan di RecSys yang sedikit kurang dikenal.dipertajam pada subjek ini. Dan dalam artikel ini kita akan berbicara tentang bagaimana ilmu ini berkembang, metode apa yang digunakan dalam rekomendasi dulu dan sekarang, dan apa matematika di balik semua ini.

Saya terinspirasi untuk menulis artikel ini dengan bekerja di StatML lab di Skoltech terkait dengan sistem recommender.

Mengapa dan untuk siapa artikel ini

Mengapa ini penting bagi kita masing-masing? Lihatlah daftar di bawah ini:

• Rekomendasi video: YouTube, Netlix, HBO, Amazon Prime, Disney +, Hulu, Okko
• Rekomendasi audio: Spotify, Yandex.Music, Yandex.Radio, Apple Music
• Rekomendasi Produk: Amazon, Avito, liter, MyBook
• Rekomendasi pencarian: Google, Yandex, Bing, Yahoo, Mail
• : Booking, Twitter, Instagram, ., , GitHub

, . , . , , YouTube.

( ), . , , . , ( ). -, . , -, , - . , . , , , , .

, , , , - . , (, , , ..). , .

, . : $$$U$ $$$I$ — . $$$r_{ui}$ $$$u$ $$$i$. , , , , . :

$$

$$\mathcal{D} = \{ (u, i) |\text{ if } \exists r_{ui}, u \in U, i \in I\}$$

$$$f$:

$$

$$f(u, i) = \hat{r}_{ui}\approx r_{ui}$$

, $$$r_{ui}$ 1 5 ( ) : 1 -1 ( / )

3 :

• Content-based (CB)
• Collaborative filtering (CF)
• Hybrid recommendations

. — , . : — , — , . . , : , ..

, . - , .

. , , , .

, , . . , , . .

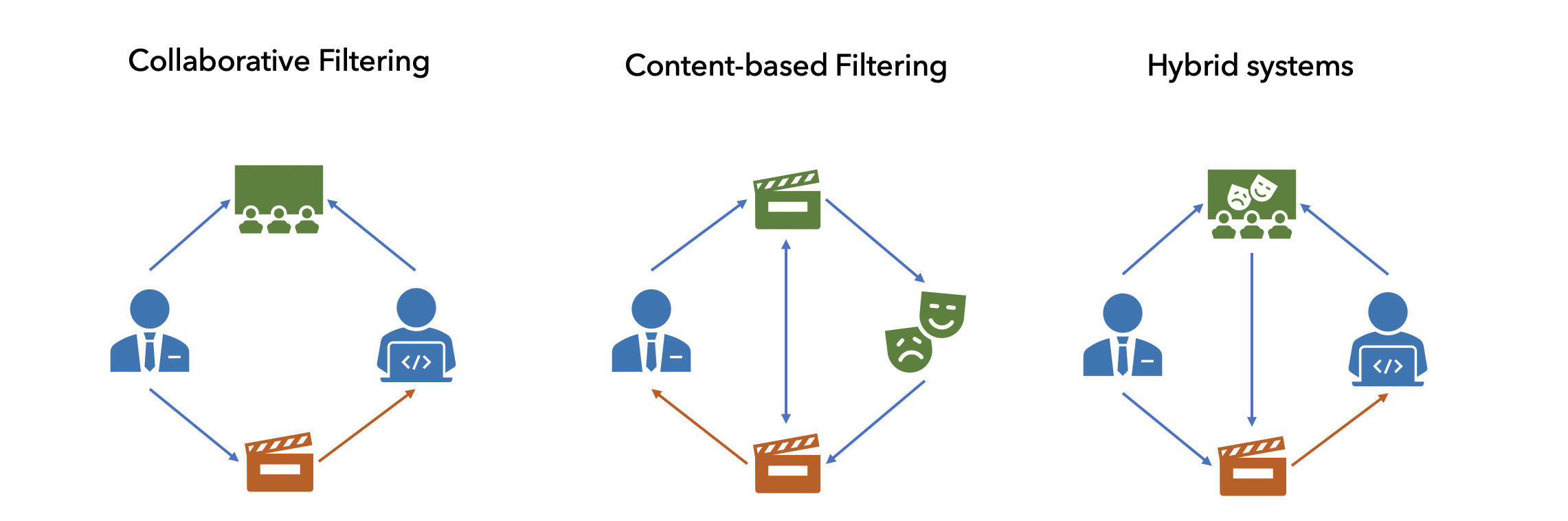
Matrix Factorization

, . : . .

• :
  
  • Singular Value Decomposition (SVD)
  • Singular Value Decomposition with implicit feedback (SVD++)
  • Collaborative Filtering with Temporal Dynamics (TimeSVD++)
  • Weighted Matrix Factorization (WMF or ALS)
  • Sparse Linear Methods (SLIM)
  • Factorization Machines (FM)
• :
  
  • Probabilistic Matrix Factorization (PMF)
  • Bayesian Probabilistic Matrix Factorization (BPMF)
  • Bayesian Factorization Machines (BFM)
  • Gaussian Process Factorization Machines (GPFM)

Singular Value Decomposition (SVD)

— SVD. $$$A$ $$$n \times m$, $$$n = |U|$, $$$m = |I|$. $$$\mathcal{D}$ $$$A_{ui} = r_{ui}$, . SVD , $$$A$ : $$$U,~\Sigma,~V$. $$$k$ , $$$A$.

$$

$$A = U \Sigma V^T, \quad\quad\quad\quad A \approx \hat{A} = \hat{U} \hat{ \Sigma } \hat{V}^T .$$

$$$Q$ $$$P$ . $$$A$ :

$$

$$P = (\hat{U} \hat{ \Sigma })^T, \quad\quad Q = \hat{V}^T, \quad\quad\quad\quad A \approx P^T \cdot Q .$$

:

$$

$$r_{ui} \approx \hat{r}_{ui} = p^T_u q_i .$$

, $$$p_u$ $$$q_i$ — $$$u$ $$$i$ - $$$k$. . . :

$$

$$\Theta = \{ p_u, q_i| u \in U, i \in I\} .$$

c :

$$

$$\sum_{(u, i) \in \mathcal{D}} (r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 = \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p^T_u q_i)^2 + \lambda\sum_{u \in U}\|p_u\|^2 + \lambda\sum_{i \in I}\|q_i\|^2 .$$

, , , , . $$$\hat{r}_{ui}$. (GD) (ALS). Habr- , . , , .

( SVD, SVD$$$_{bias}$). , , . . SVD . (bias):

$$

$$\hat{r}_{ui} =\mu + b_u + b_i + p^T_u q_i ,$$

$$$b_u$ — , $$$b_i$ — , $$$\mu$ — . :

$$

$$\Theta = \{ \mu, b_u, b_i, p_u, q_i| u \in U, i \in I\} .$$

SVD++

Factorization Meets the Neighborhood SVD . (explicit and implicit user feedback). $$$r_{ui}$, . . : $$$R(u)$ — ( ) $$$N(u)$ — ( ).

SVD++ :

$$

$$\hat{r}_{ui} =\mu + b_u + b_i + q^T_i \left( p_u + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) .$$

:

$$

$$\Theta = \{ \mu, b_u, b_i, p_u, q_i, y_i| u \in U, i \in I\} .$$

, $$$N(u)$ $$$R(u)$, .. $$$R(u) \subset N(u)$. (item-item recommendation).

Asymmetric-SVD

SVD++ . . :

$$

$$\hat{r}_{ui} = b_{ui} + q^T_i \left( |R(u)|^{-1/2} \sum_{j \in R(u)} (r_{uj} - b_{uj})x_j + |N(u)|^{-1/2} \sum_{j \in N(u)} y_j \right) ,$$

$$$b_{ui} = \mu + b_u + b_i$

TimeSVD++

TimeSVD++. (MovieLens, Netflix) , . , . Collaborative Filtering with Temporal Dynamics SVD++ :

$$

$$\hat{r}_{ui}(t) =\mu + b_u(t) + b_i(t) + q^T_i \left( p_u(t) + |R(u)|^{-1/2} \sum_{j \in R(u)} y_j \right) .$$

Mari kita cari tahu persis bagaimana waktu mempengaruhi setiap istilah:
Bias item: Jika Anda membagi interval waktu ketika peringkat dimasukkan ke dalam segmen (30 bagian diusulkan dalam pekerjaan) dan tambahkan parameter Anda sendiri$$$b_{i,\text{Bin}(t)}$ untuk setiap produk, yang dipilih tergantung pada interval di mana variabel $$$t$:

$$

$$b_i(t) = b_i + b_{i, \text{Bin}(t)}$$

Bias pengguna: Menganalisis data Neflix, kami perhatikan bahwa untuk setiap pengguna rata-rata hanya ada 40 hari di mana ia memberikan peringkat. Karena itu, kami akan bertindak seperti barang dan menambahkan parameter kami sendiri$$$b_{u, t}$untuk setiap pengguna. Kami menambahkan ketergantungan linear pada waktu - kami memperkenalkan istilah tambahan$$$\alpha_u$ dengan rasio penyusutan:

$$

$$b_i(t) = b_i + \alpha_u \cdot \text{dev}_u(t) + b_{u, t} \quad\quad\quad\quad \text{dev}_u(t) = \text{sign}(t - t_u) \cdot |t - t_u|^{\beta}$$

.
Ada opsi lain tentang cara menambahkan ketergantungan waktu kepada pengguna: Ini dijelaskan secara lebih rinci di artikel
Pengguna embeddings: kami akan menambahkan trik serupa untuk setiap komponen representasi laten kami$$$p_u(t) = (p_{u1}(t), \dots, p_{uf}(t))^T$:

$$

$$p_{uk}(t) = p_{uk} + \alpha_{uk} \cdot \text{dev}_u(t) + p_{uk, t}.$$

Weighted Matrix Factorization (WMF) & Alternating Least Squares (ALS)

Salah satu masalah utama yang dimiliki SVD adalah penggunaan hanya respons eksplisit dari pengguna. Masalah ini sebagian diselesaikan di SVD ++ . Tetapi ada cara lain - Weighted Matrix Factorization ( WMF ). Pada artikel ini , mereka menyarankan hampir tidak mengubah model ($$$\hat{r}_{ui} = p^T_u q_i$), dan mengubah proses pembelajaran. Tetapkan peringkat$$$r_{ui}$yang tidak kita ketahui (yaitu untuk pasangan $$$(u, i) \notin \mathcal{D}$) nilainya 0. Dan kemudian untuk setiap pasangan $$$(u, i)$ masukkan parameter $$$c_{ui}$, $$$r_{ui}$. , . - . YouTube , . , , , . , , , :

$$

$$\sum_{(u, i)} c_{ui}(r_{ui} - \hat{r}_{ui})^2 + \lambda\sum_{\theta \in \Theta}\|\theta\|^2 .$$

: $$$c_{ui} = 1 + \alpha r_{ui}$. : $$$r_{ui}>0$ $$$r_{ui} = 0$. $$$\alpha$ $$$\alpha = 40$ .

, (ALS) . WMF, ALS, .

Fast Alternating Least Squares

ALS , eALS . , . , . .

, $$$c_{ui}$ ALS :

$$

$$c_{ui} = c_i + \alpha r_{ui}, \quad\quad\quad\quad c_i = c_0 \frac{f_i^{\beta}}{\sum_{j \in I} f_j^{\beta}} ,$$

$$$c_0$ $$$\beta$, .

Sparse Linear Methods (SLIM)

Sparse Linear Methods (SLIM) . , SVD . . SLIM :

$$

$$\hat{a}_{ui} = a^T_u w_i \quad\quad\quad\quad \hat{A} = AW$$

$$$W \in \mathbb{R}^{m \times m}$. : $$$W \geq 0$ $$$\text{diag}(W) = 0$. :

$$

$$\frac{1}{2}\|A - AW\|^2_F + \frac{\beta}{2}\|W\|^2_F + \lambda\|W\|_1$$

$$$W$ .

Factorization Machines (FM)

, Factorization Machines (FM). , ( 2- ). :

$$

$$\hat{r}(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{i=j+1}^{n} v^T_i v_j ~ x_i x_j, \quad\quad\quad\quad w_0 \in \mathbb{R} ~~~ w \in \mathbb{R}^n ~~~ V \in \mathbb{R}^{n \times k} .$$

(SGD) ( ). , $$$x$ $$$(u, i)$. . , — . — ( ). ( ).

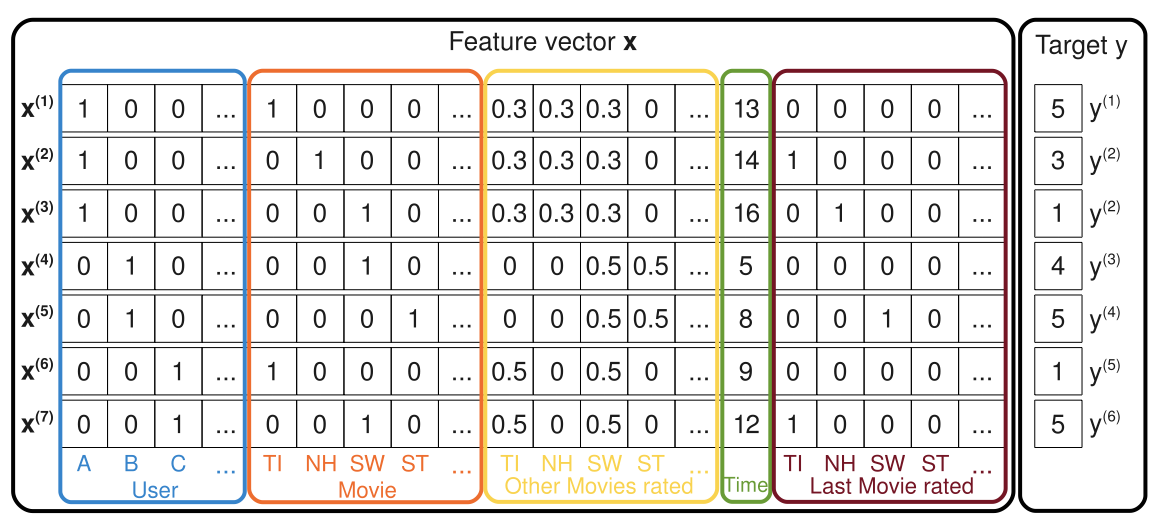
, SVD, SVD++ — FM. SVD , :

$$

$$n = | U \cup I |, \quad\quad\quad x_j = \delta (j = u ~\lor~ j = i) .$$

$$$\delta$ — . .. $$$x$ $$$u$ $$$i$. FM :

$$

$$\hat{r}(x) = w_0 + w_u + w_i + v^T_u v_i .$$

, $$$x$: , . , , , , , , . .

Probabilistic Matrix Factorization (PMF)

, , , .

(PMF), . , SVD: $$$p_u$ $$$q_i$ — . , :

$$

$$p(r | P, Q, \sigma) = \prod_{(u, i) \in \mathcal{D}}\mathcal{N}(r_{ui}| g(p_u^Tq_i), \sigma^2) ,$$

$$$\mathcal{N}$ — , a $$$g(x) = \frac{1}{1 + e^{-x}}$ — (). , , :

$$

$$p(P| \sigma_p) = \prod_{u \in U} p(p_u| 0, \sigma^2_p \mathbf{I}), \quad\quad\quad\quad p(Q| \sigma^2_q) = \prod_{i \in I} p(q_i| 0, \sigma_q^2 \mathbf{I}) .$$

( ) , :

$$

$$\frac{1}{2} \sum_{(u, i) \in \mathcal{D}} (r_{ui} - p_u^T q_i)^2 + \frac{\lambda_p}{2} \sum_{u \in U} \|p_u\|^2 + \frac{\lambda_q}{2} \sum_{i \in I} \|q_i\|^2 ,$$

$$$\lambda_p = \frac{\sigma_p}{\sigma}$ $$$\lambda_q = \frac{\sigma_q}{\sigma}$ — . , SVD , .

Constrained PMF

PMF Constrained PMF. , SVD SVD++. , , $$$p_u$ :

$$

$$p_u + \frac{\sum_{i \in R(u)} y_i}{|R(u)|} ,$$

$$$R(u)$ — , $$$u$.

Bayesian Probabilistic Matrix Factorization (BPMF)

PMF BPMF. PMF , , . :

$$

$$p(P| \mu_p, \Lambda_p) = \prod_{u \in U} p(p_u| \mu_p, \Lambda_p) ,\quad\quad\quad\quad p(Q| \mu_q, \Lambda_q) = \prod_{i \in I} p(q_i| \mu_q, \Lambda_q) .$$

$$$\Theta_p = \{ \mu_p, \Lambda_p \}$ $$$\Theta_q = \{ \mu_q, \Lambda_q \}$ - $$$\Theta_0 = \{ \mu_0, \nu_0, W_0 \}$. , .

Bayesian Factorization Machines (BFM)

, Bayesian, . , $$$\Theta = \{ w_0, w_i, v_i\} .$ , - . : $$$\Theta_H = \{ \lambda_{\theta}, \mu_{\theta} | \theta \in \Theta \}$. .

Gaussian Process Factorization Machines (GPFM)

GPFM . $$$f$ $$$\theta$. $$$\theta_u$ , , :

$$

$$\hat{r}_{ui} = f(q_i, \theta_u)$$

, . , $$$f$ , . , , , .

.

: Bayesian Personalized Ranking (BPR)

BPR , "". , BPR — , , Bayesian Personalized Ranking. . , , $$$i$ $$$j$ $$$u$. $$$(u, i)$ $$$r_{ui}$ $$$(u, i, j)$ $$$i$ $$$j$ ((+) $$$i$ , $$$j$ (-) ). $$$\mathcal{D}_S$. . ( personalized ):

$$

$$p(i <_u j | \Theta) = \sigma(\hat{r}_{uij}(\Theta)) ,$$

$$$\sigma$ — , a $$$\hat{r}_{uij}$ — . (MLE), , :

$$

$$\min_{\Theta} \sum_{(u, i, j) \in \mathcal{D}_S}\ln{\sigma(\hat{r}_{uij})} - \lambda \|\Theta\|^2$$

(SGD):

$$

$$\Theta \leftarrow \Theta + \alpha\left(\frac{e^{-\hat{r}_{uij}}}{1 + e^{-\hat{r}_{uij}}} \cdot \frac{\partial}{\partial \Theta}\hat{r}_{uij} + \lambda \Theta \right)$$

, . , , . SVD:

$$

$$\hat{r}_{uij} = \hat{r}_{ui} - \hat{r}_{uj} \quad\quad\quad\quad \hat{r}_{ui} = p_u^T q_i$$

:

$$

$$\frac{\partial}{\partial \Theta}\hat{r}_{uij} =\begin{cases} (q_{ik} - q_{jk})~~~\text{if } \theta = p_{uk}\\ p_{uk}~~~~~~~~~~~~~~~\text{if } \theta = q_{ik}\\ -p_{uk}~~~~~~~~~~~~\text{if } \theta = q_{jk} \end{cases}$$

BPR ( ) , . , . . , (pairwise approach) (pointwise approach). . , 5 , . , , . — BPR - , . , .

Show must go on

Kali ini kami membahas banyak metode Faktorisasi dalam sistem rekomendasi, tetapi Grafik dan Jaringan Saraf Tiruan , yang juga memiliki banyak hal menarik , tetap tidak tersentuh .