Coderikएक बार नोट किया: "बहुत सारे कलमन फ़िल्टर कभी नहीं होते हैं । " बेयस के प्रमेय के बारे में भी यही कहा जा सकता है, क्योंकि एक ओर यह इतना सरल है, लेकिन दूसरी ओर इसकी गहराई को समझना इतना कठिन है।

YouTube का एक शानदार छात्र डेव चैनल है , लेकिन अंतिम वीडियो छह साल पहले पोस्ट किया गया था। चैनल में शैक्षिक वीडियो शामिल हैं जिसमें लेखक बहुत ही सरल भाषा में जटिल बातें बताता है: बेयस प्रमेय, कलमन फ़िल्टर, आदि छात्र डेव ने अपनी कहानी को मटलब में गणना के उदाहरण के साथ पूरक किया।

एक बार जब उनका वीडियो सबक "इरेटीव बेयसियन असेसमेंट" कहलाता है, तो इससे मुझे बहुत मदद मिली (चैनल पर यह प्लेलिस्ट से मेल खाती है "इटरटिव बेयसियन आकलन: MATLAB के साथ") मैं चाहता था कि सभी लोग डेव के स्पष्टीकरण से परिचित हों, लेकिन दुर्भाग्य से परियोजना समर्थित नहीं है। दवे खुद संपर्क में नहीं आते। आप वीडियो में अनुवाद नहीं जोड़ सकते, क्योंकि यह लेखक द्वारा स्वयं शुरू किया जाना चाहिए। संपर्क करने पर youtube ने परिणाम नहीं दिया, इसलिए मैंने रूसी में एक लेख में सामग्री का वर्णन करने और इसे प्रकाशित करने का निर्णय लिया, जहां इसे सबसे अधिक सराहना मिली। सामग्री बहुत अधिक संशोधित और पूरक है, क्योंकि यह मेरी व्यक्तिपरक धारणा के माध्यम से चली गई है, इसलिए इसे अनुवाद के रूप में रखना अनुचित होगा। लेकिन मैंने डेव से स्पष्टीकरण का बहुत नमक लिया। मैंने अजगर में इसके कोड को फिर से लिखा है, क्योंकि मैं खुद इसमें काम करता हूं और इसे गणितीय पैकेजों का एक अच्छा विकल्प मानता हूं।

इसलिए, यदि आप बेयस प्रमेय के विषय की गहरी समझ बनाना चाहते हैं, तो स्वागत है।

समस्या का निरूपण

, “ ”. .

-, . , . , . . , . . - .

, , , .

- $x$ . $x = 3$ . . .

( ) $N = 100$ () .

$\sigma_y^2=4$ .
, .

f_{p o s t e r i o r} (x) = \frac{f_{p r i o r} (x) \cdot f_{и з м} (x)}{\int f_{p r i o r} (x) \cdot f_{m e s} (x) d x},

$\begin{equation} f_{posterior}(x) = \frac{f_{prior}(x) \cdot f_{}(x)}{\int f_{prior}(x) \cdot f_{mes}(x) dx}, \end{equation}$

$f_{posterior}(x)$ — ;
$f_{prior}(x)$ — ;
$f_{mes}(x)$ — ( $L_x(sample)$ ).
. , ( , ):

f_{m e s} (x) = p d f (x = y, μ = x, σ = σ) = \frac{1}{2 π σ} e^{- \frac{(y - x)^{2}}{2 σ^{2}}},

$\begin{equation} f_{mes}(x) =pdf(x=y, \mu=x, \sigma=\sigma) = \frac{1}{2 \pi \sigma} e^{- \frac{(y-x)^2}{2\sigma^2}}, \end{equation}$

$pdf$ — ;
$\mu$ — ;
$\sigma$ — ;
$y$ — .
( $N$ ), , .

.
$\sigma$ , 99,7 %.

- , .

. -.
$(3, 5)$ . ( ) .

() , . .

:

f_{p o s t e r i o r} (X) = \frac{f_{p r i o r} (X) \cdot f_{и з м} (X)}{\int f_{p r i o r} (X) \cdot f_{m e s} (X) d X},

$\begin{equation} f_{posterior}(X) = \frac{f_{prior}(X) \cdot f_{}(X)}{\int f_{prior}(X) \cdot f_{mes}(X) dX}, \end{equation}$

$X$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ ;
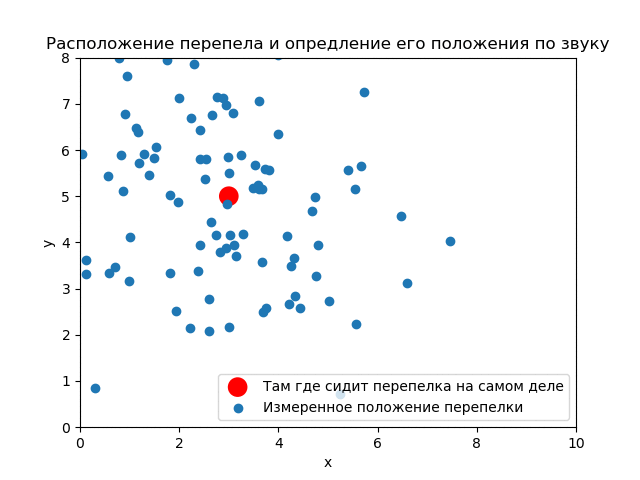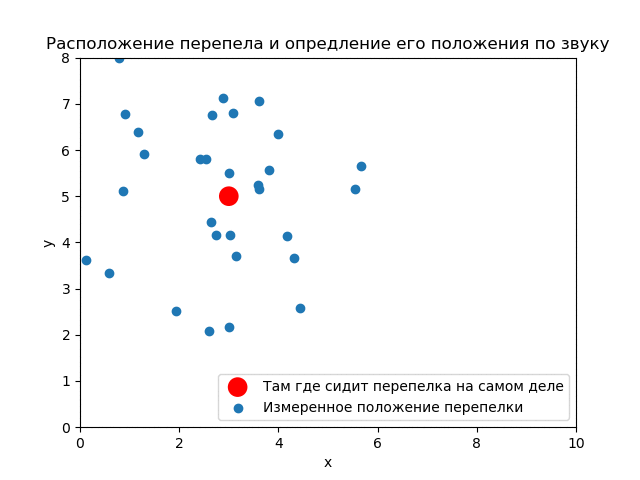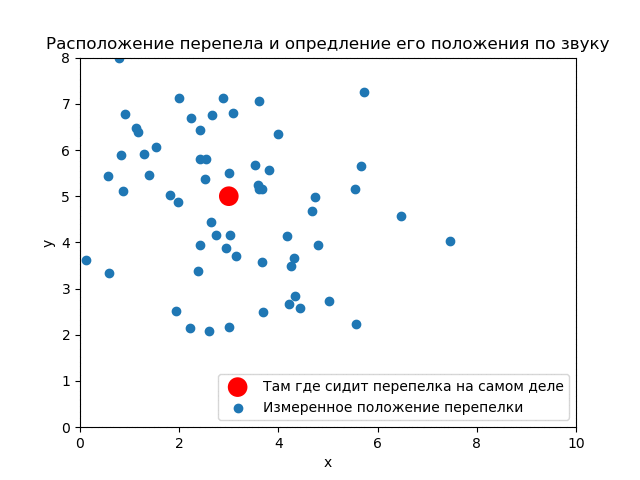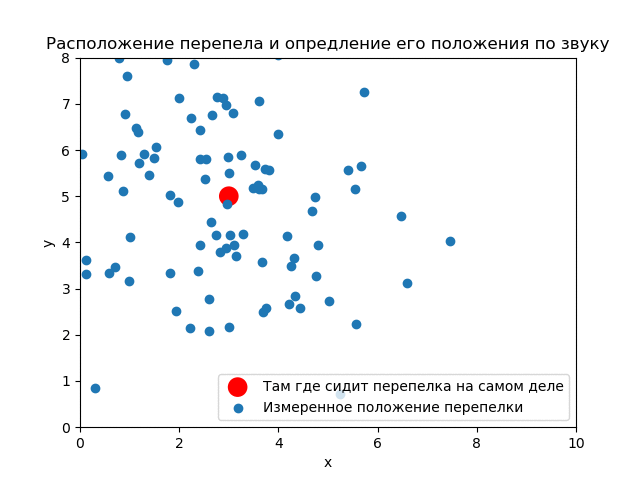
$f_{posterior}(X)$ — ;
$f_{prior}(X)$ — ;
$f_{mes}(X)$ — .
:

f_{m e s} (X) = \frac{1}{(2 π)^{2} d e t K} e^{\frac{1}{2} (Y - X)^{T} K^{- 1} (Y - X)},

$\begin{equation} f_{mes}(X) = \frac{1}{(2\pi)^2 detK} e^{ \frac {1}{2} (Y-X)^T K^{-1} (Y-X)}, \end{equation}$

$K$ — ;
$Y$ — $\begin{pmatrix} x\\ y\end{pmatrix}$ .
, .

.

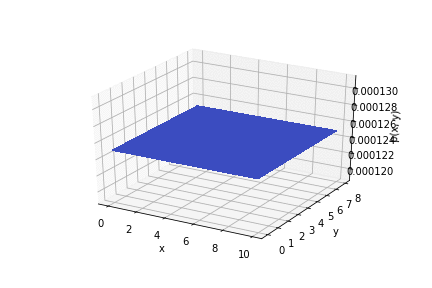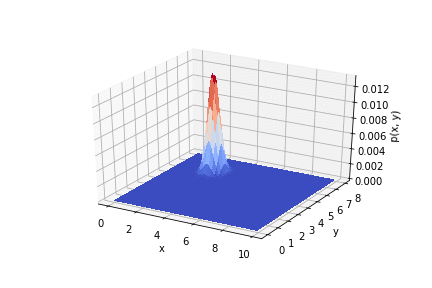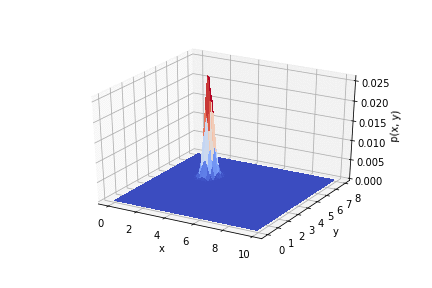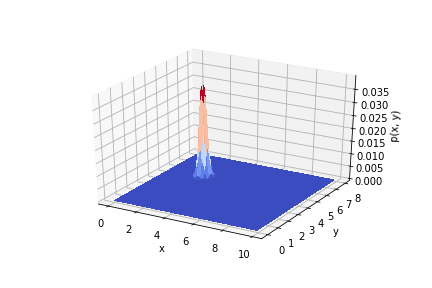
इस प्रकार, यह देखा जाता है कि प्रयोग के परिणाम एक प्राथमिकता वितरण को कैसे प्रभावित करते हैं। यदि आप माप का सही ढंग से उपयोग करते हैं, तो आप अच्छी सटीकता प्राप्त कर सकते हैं।
लेकिन क्या केवल सभी मापों का औसत निकालना आसान नहीं है और इस तरह से बटेर के स्थान का आकलन करना आसान है? बेशक। यह उदाहरण निरंतर यादृच्छिक चर के लिए बेयस प्रमेय का एक अच्छा उदाहरण है। लेख का उद्देश्य सिद्धांत को व्यवस्थित करना है।

आत्म-अलगाव के इन हफ्तों के दौरान डेव चैनल द्वारा बंद करो। सभी के लिए अच्छा है।

बायेसियन निंजा

समस्या का निरूपण

More articles: