👧🏼 🦍 🚢 इलेक्ट्रोस्टैटिक चार्ज के तनाव और आंदोलनों की रेखाओं का दृश्य, सौर मंडल के ग्रहों की गति का अनुकरण 🍍 ⬇️ 🧙🏾

नमस्ते, आज मैं आपको कुछ शारीरिक प्रक्रियाओं के मॉडलिंग के लिए एक दृश्य सहायता प्रदान करना चाहता हूं और यह दिखाता हूं कि सुंदर चित्र और एनिमेशन कैसे प्राप्त करें। बहुत सी तस्वीरों को सावधानी।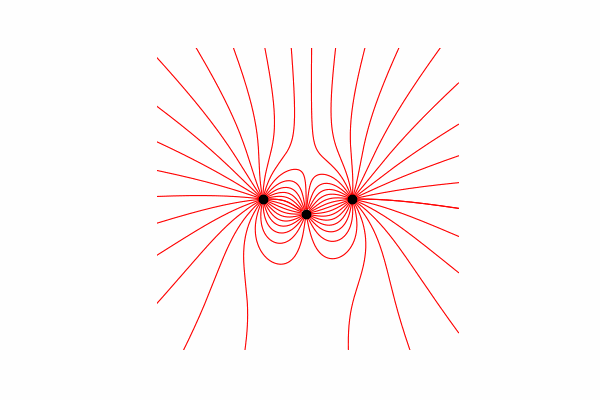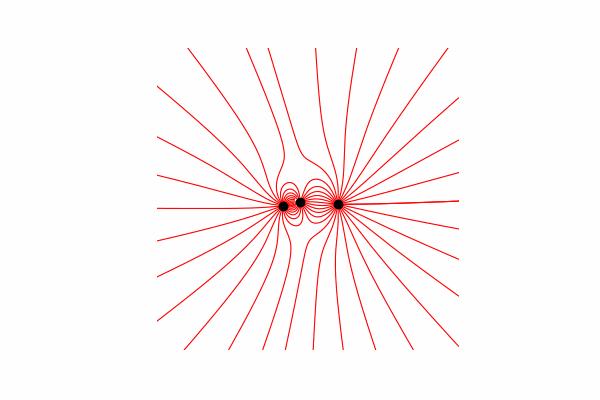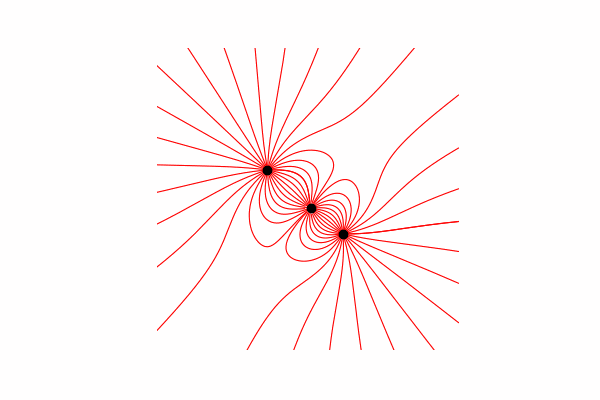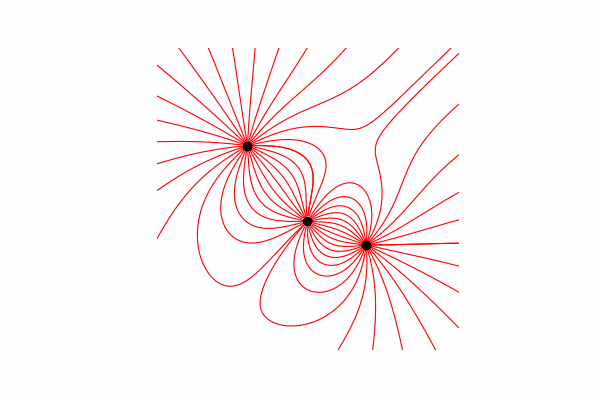

सभी कोड Google कोलाब में पाए जा सकते हैं ।

सिद्धांत

सबसे पहले, हमें इस विषय पर एक छोटी सैद्धांतिक न्यूनतम आवश्यकता है। आइए यह समझने से शुरू करें कि तनाव की रेखाएं क्या हैं और उन्हें कैसे गिनें। वास्तव में, ये रेखाएँ कई टेंशन वैक्टरों का विलय हैं, जिनकी गणना निम्न प्रकार से की जा सकती है: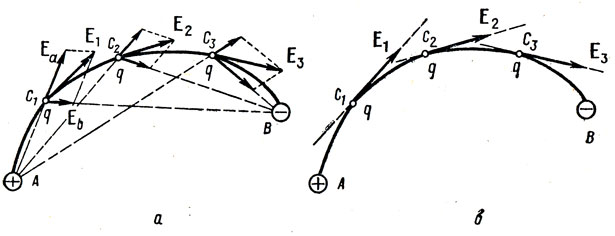

E = \frac{k * | q |}{r^{2}}

$E=\frac{k*|q|}{r^2}$ ।

ई गणना विधि

मैंने त्रिकोणों की समानता के माध्यम से तनाव वेक्टर की गणना की, जिससे क्रमशः x और y अक्षों dx और डाई पर अनुमान प्राप्त किए।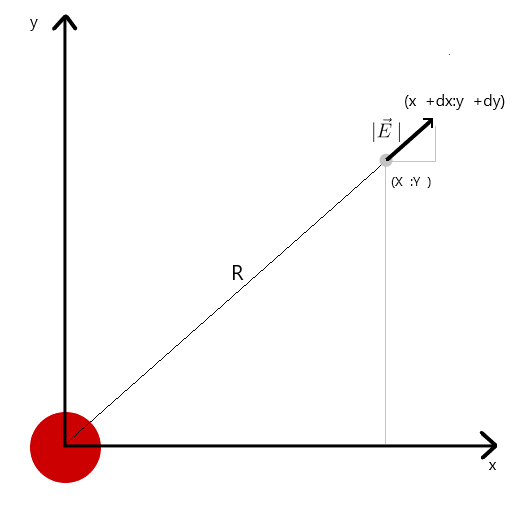

समानता से यह निम्नानुसार है कि अंतरिक्ष में आर से बिंदु तक वेक्टर की त्रिज्या और तीव्रता वेक्टर वेक्टर की लंबाई क्रमशः इन वैक्टर (X1 और dx) के अनुमानों के अनुपात के बराबर है

\frac{R}{E} = \frac{x}{d x} = \frac{y}{d y}

$\frac{R}{E}=\frac{x}{dx}=\frac{y}{dy}$ । परिणामस्वरूप वेक्टर का फॉर्मूला

\vec{E} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{E}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{E}}_{i} |}{R_{i}} \end{matrix})

$\vec{E}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{E}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{E}_i|}{R_i} \end{array}\right) \qquad$
इस ज्ञान के साथ हमें पहला परिणाम मिलता है।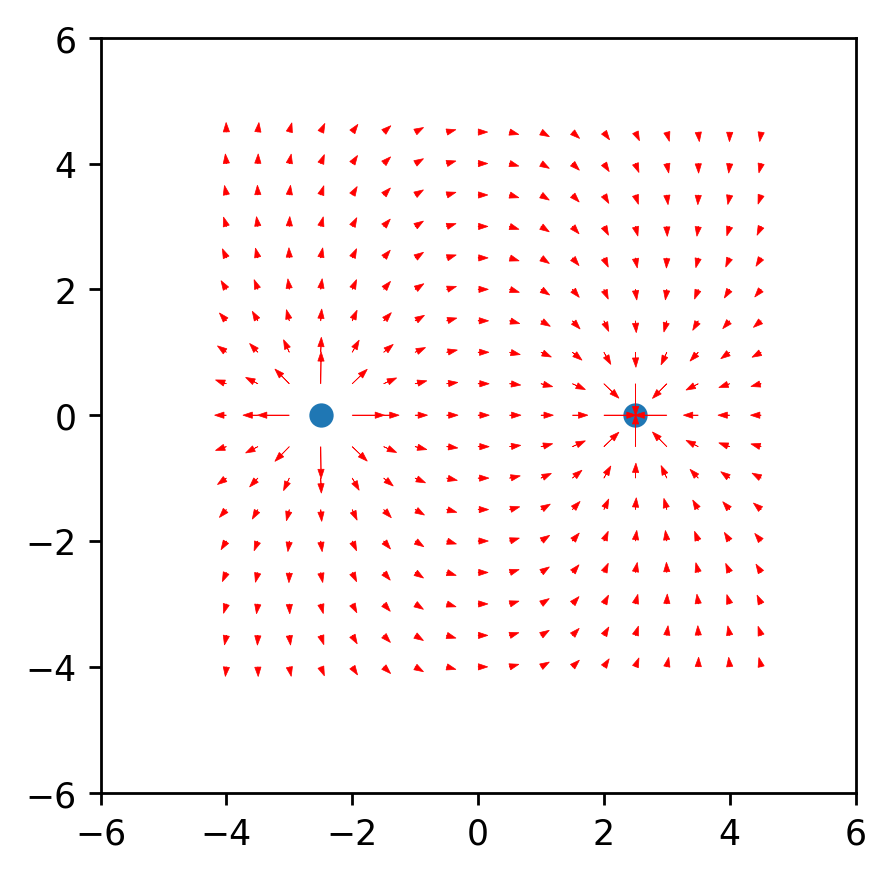

प्रोजेक्शन गणना समारोह

def E(q_prop, xs, ys, nq): #q_prop=[[xq1, yq1, q1, mq1, vxq1, vyq1], [xq2, yq2, q2, mq2, vxq2, vyq2] ... ] 
    l=1
    k=9*10**9
    Ex=0
    Ey=0
    c=0
    for c in range(len(q_prop)):#                
        q=q_prop[c]
        r=((xs-q[0])**2+(ys-q[1])**2)**0.5
        dEv=(k*q[2])/r**2
        dEx=(xs-q[0])*(dEv/r)*l
        dEy=(ys-q[1])*(dEv/r)*l

        Ex+=dEx
        Ey+=dEy
    return Ex, Ey

लाइन निर्माण विधि

पहले आपको स्टार्ट और एंड पॉइंट पर निर्णय लेने की आवश्यकता है कि लाइन और डॉक कहां से जाएंगे। शुरुआत चार्ज के चारों ओर एक त्रिज्या आर के साथ एक सर्कल पर होती है, और अंतिम बिंदु आरोपों के अलावा आर से अधिक नहीं होते हैं।

अंक शुरू करने के लिए कोड

theta = np.linspace(0, 2*np.pi, n)
mask=q_prop[ q_prop[:,2]>0 ]#    
for cq in range(len(mask)):
    qmask=mask[cq]
    xr = r_q*np.cos(theta)+qmask[0]# -    
    yr = r_q*np.sin(theta)+qmask[1]#

तो यह कहने योग्य है कि लाइनें केवल सकारात्मक शुल्क से निर्मित हैं।

और अंत में, लाइनों का निर्माण। ऐसा करने के लिए, हम शुरुआती बिंदु से उसमें तनाव की वेक्टर की रेखा का निर्माण करते हैं, निर्माण बिंदु के अंत में शुरुआती बिंदु को अपडेट करते हैं और तब तक दोहराते हैं जब तक कि ऊपर वर्णित अंतिम स्थितियां नहीं पहुंच जाती हैं।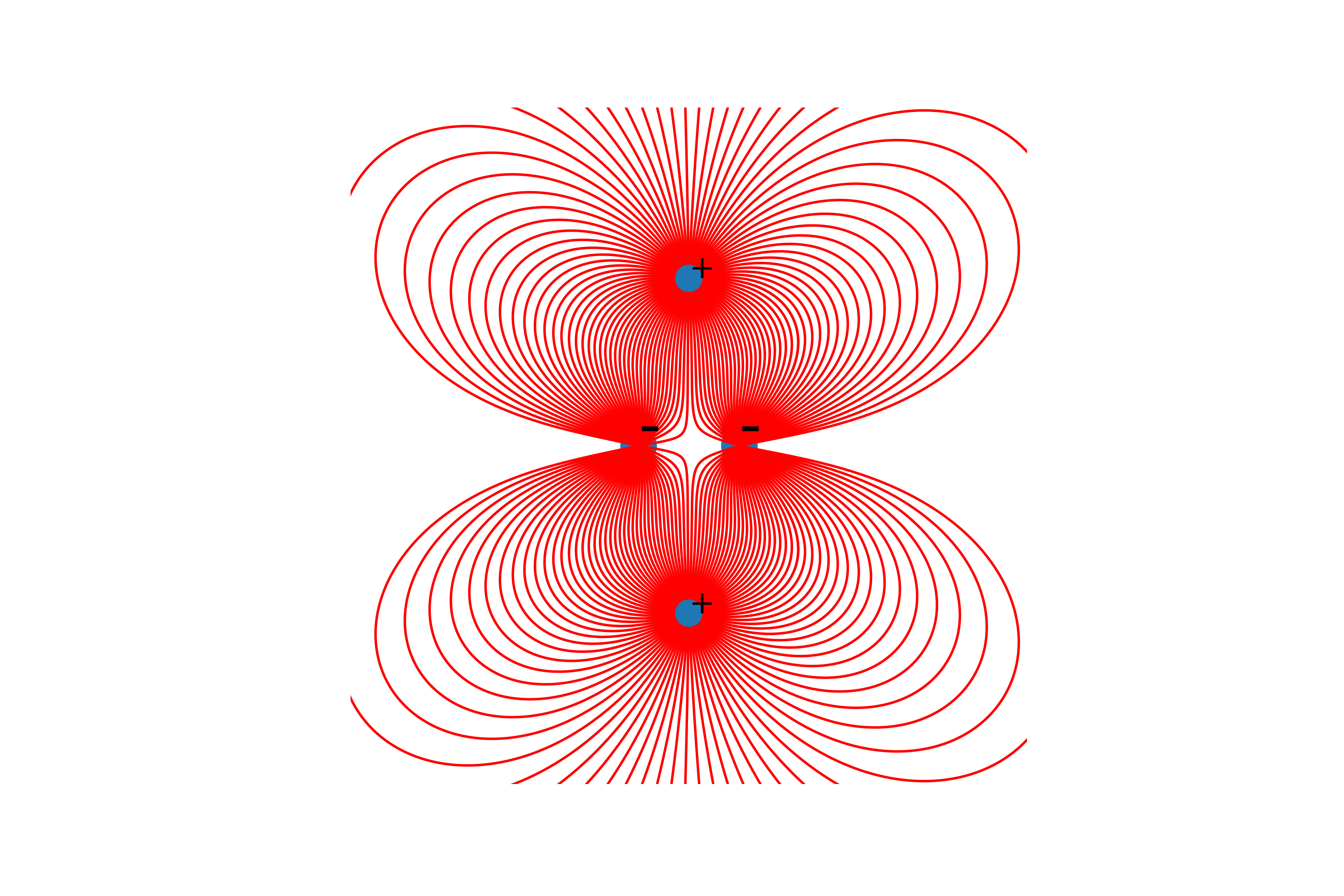

लाइन समन्वय गणना समारोह

def Draw(size, q_prop,r_q, n):
  
  linen=np.empty((np.count_nonzero(q_prop[:,2]>0),n, 2000000), dtype=np.float64)
  linen[:] = np.nan
  theta = np.linspace(0, 2*np.pi, n)
  mask=q_prop[ q_prop[:,2]>0 ][ q_prop[q_prop[:,2]>0][:,3]==1 ]
  for cq in range(len(mask)):
    qmask=mask[cq]
    x11 = r_q*np.cos(theta)+qmask[0]
    x22 = r_q*np.sin(theta)+qmask[1]
    for c in range(len(x11)):

      xs=x11[c]
      ys=x22[c]

      lines=np.empty((2,1000000), dtype=np.float64)
      lines[:]=np.nan
      stop=0
      nnn=0
      
      lines[0][nnn]=xs
      lines[1][nnn]=ys
      while  abs(xs)<size+2 and abs(ys)<size+2: 
        nnn+=1

        for cq1 in range(len(q_prop)):
          q=q_prop[cq1]
          if ((ys-q[1])**2+(xs-q[0])**2)**0.5<r_q/2 :
            stop=1
            break
        if stop==1:
          break
        dx, dy = E1(q_prop,xs,ys)

        xs+=dx
        ys+=dy
        lines[0][nnn]=xs
        lines[1][nnn]=ys
       
      linen[cq,c,:]=lines.reshape(-1)

  return linen

आरोपों के बीच बातचीत

उनकी बातचीत को प्रतिबिंबित करने के लिए, प्रत्येक छोटे समय के बाद अपने निर्देशांक और गति को बदलना आवश्यक है।

x + = \frac{E_{x} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{x} \cdot d t

$x+=\frac{E_x \cdot q \cdot dt^2}{2\cdot m} + v_x\cdot dt$

y + = \frac{E_{y} \cdot q \cdot d t^{2}}{2 \cdot m} + v_{y} \cdot d t

$y+=\frac{E_y \cdot q \cdot dt^2}{2\cdot m} + v_y \cdot dt$

v_{x} + = \frac{E_{x} \cdot q \cdot d t}{m}

$v_x+= \frac{E_x \cdot q \cdot dt}{ m}$

v_{y} + = \frac{E_{y} \cdot q \cdot d t}{m}

$v_y+= \frac{E_y \cdot q \cdot dt}{ m}$

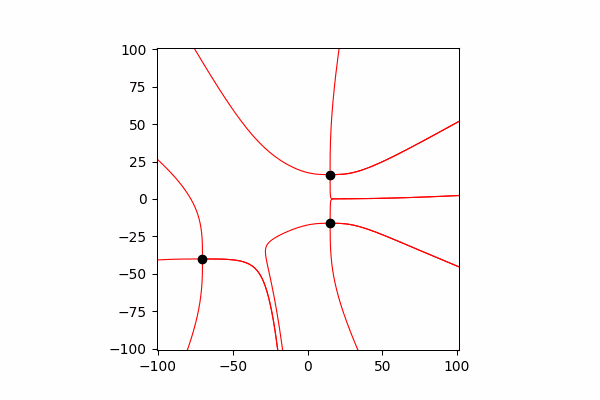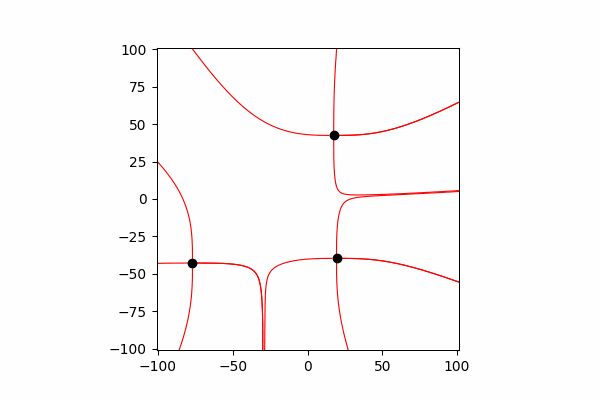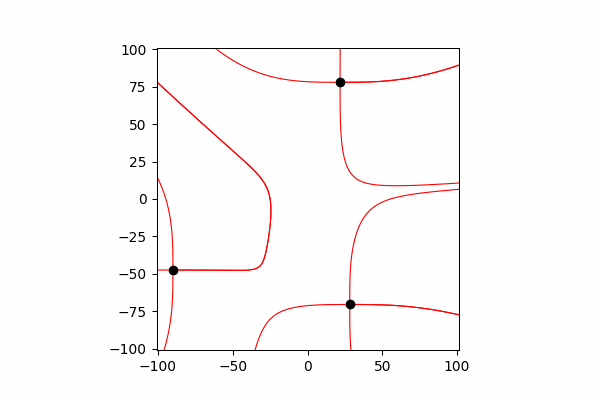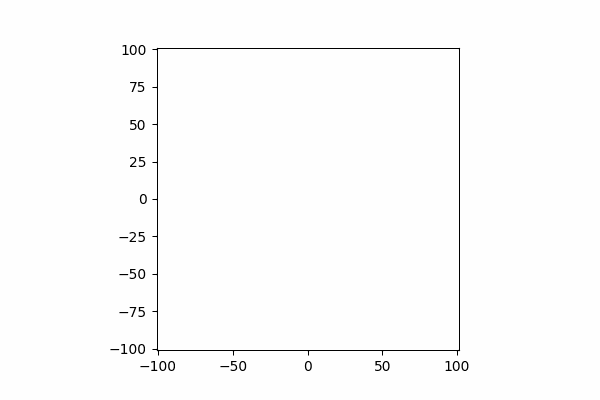
निर्देशांक और चार्ज गति के अनुमानों को अपडेट करने का कार्य

def Update_all(q_prop):
  vx=0
  vy=0
  x=0
  y=0
  q_prop_1=np.copy(q_prop)
  for c in range(len(q_prop)):#         
    xs=q_prop[c][0]
    ys=q_prop[c][1]
    q =q_prop[c][2]
    m =q_prop[c][3]
    vx=q_prop[c][4]
    vy=q_prop[c][5]
    Ex, Ey= E(q_prop, xs, ys, c)

    x=(((Ex*q)/m)*dt**2)/2+vx*dt+xs
    y=(((Ey*q)/m)*dt**2)/2+vy*dt+ys
    vx+=((Ex*q)/m)*dt
    vy+=((Ey*q)/m)*dt
    #print(q_prop[c]-[x,y,q,m,vx,vy])
    q_prop_1[c]=[x,y,q,m,vx,vy]
  
  return q_prop_1#

गुरुत्वाकर्षण

मौजूदा कोड के आधार पर, मैंने एक सिम्युलेटर लिखा जो गुरुत्वाकर्षण के प्रभाव में निकायों के आंदोलनों को दर्शाता है। कोड में बदलाव मुख्य रूप से तनाव कार्य के लिए है त्वरण अब एक समान सूत्र का उपयोग करने पर विचार किया जाएगा।

g = \frac{G * m}{r^{2}}

$g=\frac{G*m}{r^2}$

\vec{g} = (\begin{matrix} \sum_{i = 0}^{N} \frac{x_{i} * | {\vec{g}}_{i} |}{R_{i}} \\ \sum_{i = 0}^{N} \frac{y_{i} * | {\vec{g}}_{i} |}{R_{i}} \end{matrix})

$\vec{g}=\left(\begin{array}{c} \sum_{i=0}^{N}\frac{x_i*|\vec{g}_i|}{R_i} \\ \sum_{i=0}^{N}\frac{y_i*|\vec{g}_i|}{R_i} \end{array}\right) \qquad$

ग्रह एक्स अक्ष से पेरीहेलियन दूरी और पेरीहेलियन गति से शुरू होते हैं। ग्रहों के सभी मान और निर्देशिका से सूर्य (द्रव्यमान, दूरी, छोर)।

पहले 4 ग्रहों + सूर्य के लिए एनीमेशन।

आलोचना और सुझावों की प्रतीक्षा है। अलविदा।

इलेक्ट्रोस्टैटिक चार्ज के तनाव और आंदोलनों की रेखाओं का दृश्य, सौर मंडल के ग्रहों की गति का अनुकरण

सिद्धांत

ई गणना विधि

लाइन निर्माण विधि

आरोपों के बीच बातचीत

गुरुत्वाकर्षण

More articles: