गहन सीखने के लिए डेटा प्रस्तुत करने की जटिलता हर दिन बढ़ रही है। ग्राफ न्यूरल नेटवर्क ( जीएनएन ) हाल के वर्षों की सफलताओं में से एक बन गया है। लेकिन वास्तव में ग्राफ़ मशीन सीखने में अधिक से अधिक लोकप्रियता क्यों प्राप्त कर रहे हैं?
मेरी कथा का अंतिम लक्ष्य मशीन सीखने की तकनीक में रेखांकन की एक सामान्य प्रस्तुति है। लेख एक वैज्ञानिक काम करने का दिखावा नहीं करता है जो रेखांकन की पूरी शक्ति का पूरी तरह से वर्णन करता है, लेकिन केवल पाठक को इस अद्भुत और जटिल दुनिया से परिचित कराता है। प्रकाशन एकदम सही है, दोनों ही युद्ध-ग्रस्त पेशेवरों के लिए, जो अभी तक गहन शिक्षा में ग्राफ़ की प्रस्तुति से परिचित नहीं हैं, और इस क्षेत्र में शुरुआती लोगों के लिए।
परिचय
किसी समस्या को हल करने के लिए आवश्यक महत्वपूर्ण विशेषताओं को स्वचालित रूप से उजागर करना मशीन सीखने के सफल उपयोग के मुख्य कारणों में से एक है। लेकिन परंपरागत रूप से, जब रेखांकन के साथ काम करते हैं, तो मशीन सीखने के दृष्टिकोण ने संरचनात्मक संरचनात्मक जानकारी की कोडिंग सुविधाओं को निकालने के लिए उपयोगकर्ता-परिभाषित हेयूरिस्टिक्स पर भरोसा किया है। फिर भी, हाल के वर्षों की प्रवृत्ति बदल गई है: दृष्टिकोण तेजी से उभर रहे हैं जिसमें वे स्वचालित रूप से गहन शिक्षण और गैर-रैखिक आयाम में कमी के तरीकों का उपयोग करके कम-आयामी निवेशों में ग्राफ संरचना को कोड करना सीखते हैं।
ग्राफ पर मशीन सीखने में, दो केंद्रीय समस्याओं को अलग किया जा सकता है: मॉडल में ग्राफ की संरचना के बारे में जानकारी का समावेश (यानी, फीचर वेक्टर में इस जानकारी को एन्कोड करने का एक सरल तरीका) और फीचर वेक्टर के आयाम में कमी।
रेखांकन से संरचनात्मक जानकारी निकालने के लिए, पारंपरिक मशीन दृष्टिकोण अक्सर ग्राफ के सारांश आंकड़ों पर आधारित होते हैं (उदाहरण के लिए, गुणांक गुणनखंडन), कर्नेल फ़ंक्शन या स्थानीय पड़ोस संरचनाओं को मापने के लिए सावधानीपूर्वक डिज़ाइन किए गए फ़ंक्शंस। हालांकि, ये दृष्टिकोण सीमित हैं, क्योंकि इन इंजीनियरिंग समाधानों को सीखने की प्रक्रिया में अनुकूलित नहीं किया जा सकता है, और उनका विकास एक श्रमसाध्य और महंगी प्रक्रिया है।
रेखांकन क्यों?
ग्राफ़ को डेटा प्रस्तुति की संरचनात्मक इकाइयों के रूप में बोलते हुए, आप अपने आप से एक साधारण सवाल पूछ सकते हैं: ग्राफ़ क्यों?
— . , , ( ) [1], [2], ( [3], [4] [5]), [6] [7].
CV/ML , , . , , [8].
, . . , , , .
, (embeddings), . , , , , (), . , , . , .
, . , , . , , , .
, (direct encoding), . . , , -. , , , .
DeepWalk node2vec . , . , .
( ). (DNGR SDNE), , [9].
, , , — ( ) , .
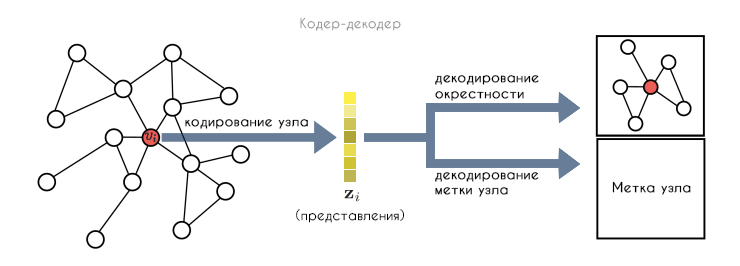
(.1). :

, , , ( , ). .
, . , ( , ). , , , , .
, , . , , . (, )
- , , / . ; ( ) , ( ). , .
, , , . , (, ) . 2 , , .
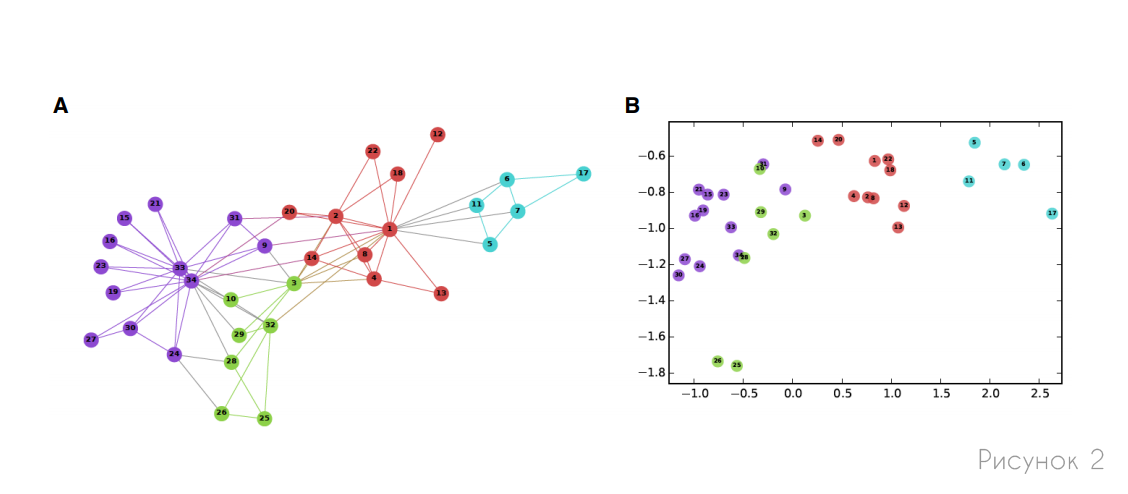
, — , , ( ):
— , :
. , , . , , . , :
— , . , , 1, 0. . ( 1) :
— , (.. ) .
, -, , . , , , , , .
seq2seq , , . , seq2seq, GNN [10].
, :
- : , .
- ENC, . , .
- DEC, .
- , , .

. , . , .
, , . , , (.3). , , , .

DeepWalk node2vec, , , . , , . , , :
— , , . , . , :
, (.. . — ( (2) ). , DeepWalk node2vec (3). DeepWalk softmax , . , node2vec (3), : , , " ".
, node2vec DeepWalk , , . , node2vec : , (.4). , . , node2vec , .
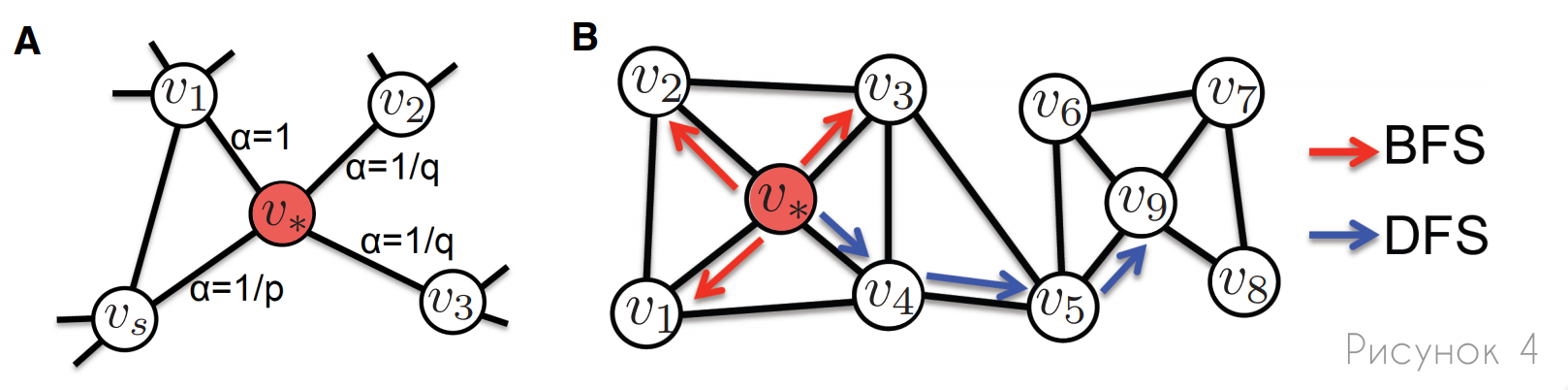
A: , node2vec , p q. , , (α) , .
B: , (BFS) (DFS). , BFS, , , . , , DFS, .
, . , :
- (.. ). , , .
- . (, ), .
- . , , ( , ). , , , , .
/ . -, , , .
(DNGR) (SDNE) , : , . , — , (.5). DNGR SDNE , .

, ( — ). . DNGR SDNE , , :
, :
, , ( ), , . SDNE, DNGR, : , (.5).
SDNE DNGR , , , . DNGR , , DeepWalk node2vec. SDNE , .
, SDNE DNGR , ( ), - . , .
, . . , , , [9], . , .
. , , , , , , .
, , , .
. (. ), ( ). . , , , , , , — , , , . , , , .
. , , - , , . , , , , .
. , , , . , , , . , .
. , , . , , . , , , . , , , , .
, — . , , .
[1] — W. L. Hamilton, Z. Ying, and J. Leskovec, "Inductive representation learning on large graphs," NIPS 2017, pp. 1024–1034, 2017.
[2] — T. N. Kipf and M. Welling, "Semi-supervised classification with graph convolutional networks," ICLR 2017, 2017.
[3] — A. Sanchez-Gonzalez, N. Heess, J. T. Springenberg, J. Merel, M. Riedmiller, R. Hadsell, and P. Battaglia, "Graph networks as learnable physics engines for inference and control," arXiv
preprint arXiv:1806.01242, 2018.
[4] — P. Battaglia, R. Pascanu, M. Lai, D. J. Rezende et al., "Interaction networks for learning about objects, relations and physics," in NIPS 2016, 2016, pp. 4502–4510.
[5] — A. Fout, J. Byrd, B. Shariat, and A. Ben-Hur, "Protein interface prediction using graph convolutional networks," in NIPS 2017, 2017, pp. 6530–6539.
[6] — T. Hamaguchi, H. Oiwa, M. Shimbo, and Y. Matsumoto, "Knowledge transfer for out-of-knowledge-base entities: A graph neural network approach," in IJCAI 2017, 2017, pp. 1802–1808.
[7] — H. Dai, E. B. Khalil, Y. Zhang, B. Dilkina, and L. Song, "Learning combinatorial optimization algorithms over graphs," arXiv preprint arXiv:1704.01665, 2017.
[8] — X. Liang, X. Shen, J. Feng, F. Lin, S. Yan, "Semantic Object Parsing with Graph LSTM", arXiv:1603.07063v1 [cs.CV] 23 Mar 2016.
[9] — Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang, Philip S. Yu, "A Comprehensive Survey on Graph Neural Networks", arXiv:1901.00596v4 [cs.LG] 4 Dec 2019.
10
संदर्भ
ग्राफ न्यूरल नेटवर्क्स: ग्राफ्स एंड अप्लीकेशन रिप्रेजेंटेशन लर्निंग ऑफ
ग्राफ्स: मेथड्स एंड एप्लीकेशन