Bonne journée.Je vous présente la traduction de l'article «Algorithmes sur les graphiques: parlons de la recherche en profondeur d'abord (DFS) et de la recherche en largeur (BFS)» de Try Khov.Qu'est-ce qu'un parcours de graphe?
En termes simples, une traversée de graphe est une transition d'un de ses sommets à l'autre à la recherche des propriétés de connexion de ces sommets. Les liens (lignes reliant les sommets) sont appelés directions, tracés, faces ou arêtes d'un graphique. Les sommets du graphique sont également appelés nœuds.Les deux principaux algorithmes de traversée de graphe sont la recherche en profondeur d'abord, DFS et la recherche en largeur d'abord, BFS.Malgré le fait que les deux algorithmes sont utilisés pour parcourir le graphique, ils ont quelques différences. Commençons par DFS.Recherche de profondeur
DFS suit le concept de «aller en profondeur, tête la première». L'idée est que nous nous déplaçons du pic de départ (point, lieu) dans une certaine direction (le long d'un certain chemin) jusqu'à ce que nous atteignions la fin du chemin ou de la destination (pic souhaité). Si nous avons atteint la fin du chemin, mais que ce n'est pas une destination, alors nous retournons (au point de chemins bifurqués ou divergents) et suivons un itinéraire différent.Regardons un exemple. Supposons que nous ayons un graphe orienté qui ressemble à ceci:
Nous sommes au point "s" et nous devons trouver le sommet "t". À l'aide de DFS, nous étudions l'un des chemins possibles, le déplaçons jusqu'à la fin et, si nous ne trouvons pas t, revenons en arrière et explorons un autre chemin. Voici à quoi ressemble le processus:
Ici, nous nous déplaçons le long du chemin (p1) jusqu'au pic le plus proche et voyons que ce n'est pas la fin du chemin. Par conséquent, nous passons au prochain pic.
Nous avons atteint la fin de p1, mais n'avons pas trouvé t, nous retournons donc à s et nous nous déplaçons le long du deuxième chemin.
Après avoir atteint le sommet du chemin «p2» le plus proche du point «s», nous voyons trois directions possibles pour un mouvement ultérieur. Puisque nous avons déjà visité le sommet couronnant la première direction, nous nous déplaçons le long de la seconde.
Nous avons de nouveau atteint la fin du chemin, mais n'avons pas trouvé t, alors nous revenons. Nous suivons le troisième chemin et, enfin, nous atteignons le pic "t" souhaité.
Voici comment fonctionne DFS. Nous nous déplaçons le long d'un certain chemin jusqu'à la fin. Si la fin du chemin est le pic souhaité, nous avons terminé. Sinon, revenez en arrière et avancez sur un chemin différent jusqu'à ce que nous explorions toutes les options.Nous suivons cet algorithme pour chaque sommet visité.La nécessité d'une répétition répétée de la procédure indique la nécessité d'utiliser la récursivité pour implémenter l'algorithme.Voici le code JavaScript:
function dfs(adj, v, t) {
if(v === t) return true
if(v.visited) return false
v.visited = true
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
let reached = dfs(adj, neighbor, t)
if(reached) return true
}
}
return false
}
Remarque: Cet algorithme DFS spécial vous permet de vérifier s'il est possible d'aller d'un endroit à un autre. DFS peut être utilisé à diverses fins. Ces objectifs détermineront l'aspect de l'algorithme lui-même. Cependant, le concept général ressemble exactement à cela.Analyse DFS
Analysons cet algorithme. Puisque nous contournons chaque «voisin» de chaque nœud, en ignorant ceux que nous avons visités précédemment, nous avons un temps d'exécution égal à O (V + E).Une brève explication de ce que V + E signifie:V est le nombre total de sommets. E est le nombre total de faces (arêtes).Il peut sembler plus approprié d'utiliser V * E, mais réfléchissons à ce que signifie V * E.V * E signifie qu'en ce qui concerne chaque sommet, nous devons étudier toutes les faces du graphique, que ces faces appartiennent ou non à un sommet particulier.En revanche, V + E signifie que pour chaque sommet, nous évaluons uniquement les arêtes qui lui sont adjacentes. Pour revenir à l'exemple, chaque sommet a un certain nombre de faces et, dans le pire des cas, on fait le tour de tous les sommets (O (V)) et on examine toutes les faces (O (E)). Nous avons V sommets et E faces, donc nous obtenons V + E.De plus, puisque nous utilisons la récursivité pour parcourir chaque sommet, cela signifie qu'une pile est utilisée (une récursion infinie entraîne une erreur de débordement de pile). Par conséquent, la complexité spatiale est O (V).Considérons maintenant le BFS.Recherche large
BFS suit le concept de "s'étendre large, s'élevant à la hauteur du vol d'un oiseau" ("aller large, vue plongeante"). Au lieu de se déplacer le long d'un certain chemin jusqu'à la fin, BFS implique d'avancer un voisin à la fois. Cela signifie ce qui suit:Au lieu de suivre le chemin, BFS signifie visiter les voisins les plus proches de s en une seule étape (étape), puis visiter les voisins des voisins et ainsi de suite jusqu'à ce que t soit détecté.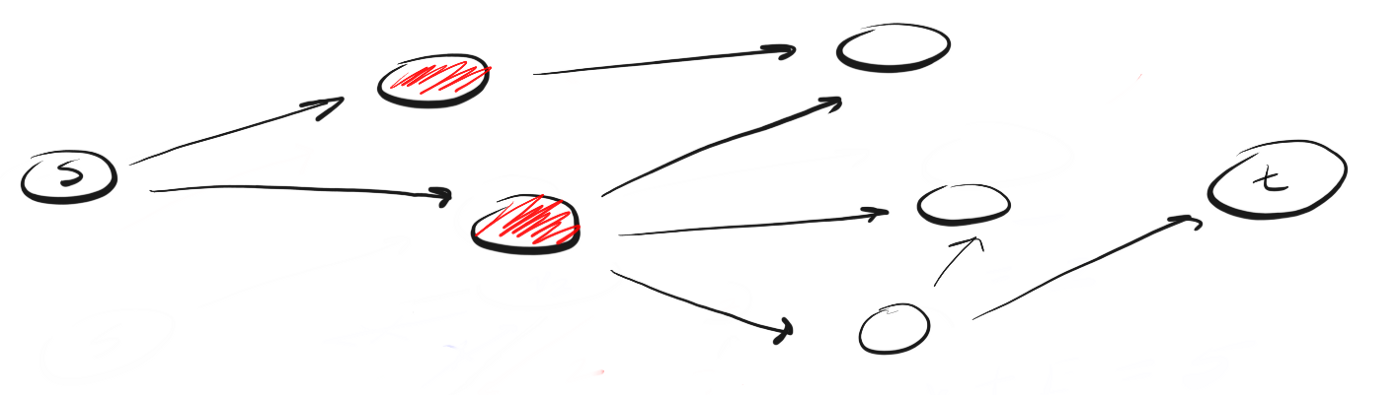
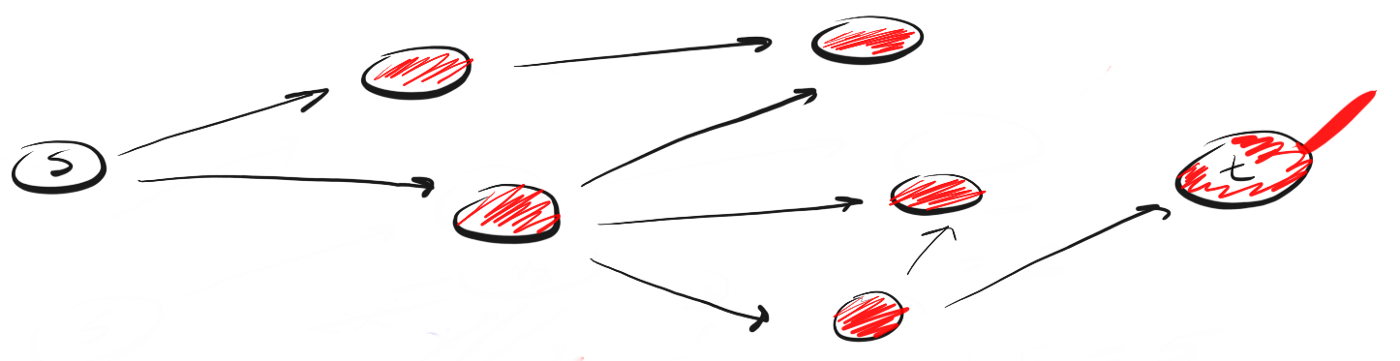En quoi DFS est-il différent de BFS? J'aime à penser que DFS va de l'avant et que BFS n'est pas pressé, mais étudie tout en une seule étape.La question se pose alors: comment savoir quels voisins doivent être visités en premier?Pour ce faire, nous pouvons utiliser le concept de "premier entré, premier sorti" (premier entré, premier sorti, FIFO) de la file d'attente. Nous mettons d'abord en file d'attente le pic le plus proche de nous, puis ses voisins non visités, et continuons ce processus jusqu'à ce que la file d'attente soit vide ou jusqu'à ce que nous trouvions le sommet que nous recherchons.Voici le code:
function bfs(adj, s, t) {
let queue = []
queue.push(s)
s.visited = true
while(queue.length > 0) {
let v = queue.shift()
for(let neighbor of adj[v]) {
if(!neighbor.visited) {
queue.push(neighbor)
neighbor.visited = true
if(neighbor === t) return true
}
}
}
return false
}
Analyse BFS
Il peut sembler que BFS est plus lent. Cependant, si vous regardez attentivement les visualisations, vous pouvez voir qu'elles ont le même temps d'exécution.Une file d'attente implique de traiter chaque sommet avant d'atteindre une destination. Cela signifie que, dans le pire des cas, BFS explore tous les sommets et faces.Malgré le fait que BFS puisse sembler plus lent, il est en fait plus rapide, car lorsque vous travaillez avec des graphiques de grande taille, il s'avère que DFS passe beaucoup de temps à suivre des chemins qui se révèlent finalement faux. BFS est souvent utilisé pour trouver le chemin le plus court entre deux pics.Ainsi, le runtime BFS est également O (V + E), et puisque nous utilisons une file d'attente contenant tous les sommets, sa complexité spatiale est O (V).Analogies réelles
Si vous donnez des analogies de la vie réelle, c'est ainsi que j'imagine le travail de DFS et BFS.Quand je pense à DFS, j'imagine une souris dans un labyrinthe à la recherche de nourriture. Pour atteindre la cible, la souris est obligée de se retrouver à plusieurs reprises dans une impasse, de revenir et de se déplacer d'une manière différente, et ainsi de suite jusqu'à ce qu'elle trouve un moyen de sortir du labyrinthe ou de la nourriture.
Une version simplifiée ressemble à ceci:
à mon tour, quand je pense à BFS, j'imagine des cercles sur l'eau. La chute d'une pierre dans l'eau entraîne la propagation de perturbations (cercles) dans toutes les directions depuis le centre.
Une version simplifiée ressemble à ceci:
résultats
- Des recherches en profondeur et en largeur sont utilisées pour parcourir le graphique.
- DFS se déplace le long des bords d'avant en arrière, et BFS se propage à travers les voisins à la recherche d'une cible.
- DFS utilise la pile et BFS la file d'attente.
- Le temps d'exécution des deux est O (V + E) et la complexité spatiale est O (V).
- Ces algorithmes ont une philosophie différente, mais sont tout aussi importants pour travailler avec des graphiques.
Remarque Per.: Je ne suis pas un spécialiste des algorithmes et des structures de données, par conséquent, si des erreurs, des inexactitudes ou des formulations incorrectes sont trouvées, veuillez écrire dans une lettre personnelle pour correction et clarification. Je serai reconnaissant.Merci de votre attention.